J Jacob Wikner ,Armin Jalili ,Sayed Masoud Sayedi ,and Rasoul Dehghani

(1.Department of Electrical Engineering,Link?ping University,SE-581 83 Link?ping,Sweden;

2.Department of Electrical and Computer Engineering,Isfahan University of Technology,Isfahan 84156-83111,Iran)

Abstract In this paper,we focus on practical issues in implementing a calibration technique for medium-resolution,high-speed flash analog-to-digital converters(ADCs).In[1],we theoretically describ the calibration technique and perform a behavioral-level simulation to test its functionality[1].In this work,we discuss some issues in transistor-level implementation.The predominant factors that contribute to static errors such as reference generator mismatch and track-and-hold(T/H)gain error can be treated as input-referred offsets of each comparator.Using the proposed calibration technique,these errors can be calibrated with minimal detriment to the dynamic performance of the converter.We simulate a transistor-level implementation of a 5-bit,1 GHz ADC in a 1.2 V,65 nm CMOS process.The results show that DNLcan be improved from 2.5 LSB to below 0.7 LSB after calibration,and INL can be improved from 1.6 LSB to below 0.6 LSB after calibration.

Keyw ords Calibration;chopping;flash ADC;PDFgenerator;reference generator circuit;track and hold circuit

1 Introduction

A flash ADCs and gave the results of a behavioral-level simulation.The simulation showed that the accuracy and resolution of the ADC could be significantly improved without detriment to the originalanalog comparator structure.In this paper,we go further by describing issues in the implementation of the ADC design and how these issues can be addressed by calibration.As we proceed in this paper,the accuracy of the calibration technique described in[1]is increased as more and more transistor-level simulations are performed.We end our work by presenting transistor-level simulation results for a 5-bit,1 GHz flash ADC in a 1.2 V,65 nm CMOSprocess.

2 Calibration Technique

The histogram-based calibration technique for flash ADCs is introduced in[1].The ADC operates in normal mode or calibration mode.In normal mode,the input signal is connected to the input of the ADC,which then converts as usual.In calibration mode,the output of the probability-density function(PDF)generator is connected to the ADC input.The PDFgenerator produces an analog signal with a known PDF,fin(x),which is further described in section 3.The output PDF,fout(x),sampled by the ADC,is a quantized version of fin(x).The output PDFis a discrete function of the number of bins per interval,Ii.Because of static errors,the two PDFs are not equal,and in our proposed histogram-based technique,this difference is used to extract the ADC errors.

We let the n-bit flash ADC have 2n-1 reference voltage levels generated by a resistor ladder.A comparator is assigned to each reference level,and each level is compared with the input signal.At the output of all 2n-1 comparators,a thermometer code is generated.Static errors are mainly caused by resistor mismatch and comparator offsets.These error components can be modeled as a voltage source,Vos,at the input of each comparator,which is now assumed to be ideal[1].

In the n-bit flash ADC using the histogram-based calibration technique,a multiplexer(MUX)array is used to select a set of comparators for calibration.The outputs of the nalog-to-digital converters(ADCs)are used in communications,instrumentation,video,and imaging.They are essential components in RF tranceivers but also performance-limiting in many systems.The accuracy of a flash ADC is mainly limited by the offsets of the comparators and references.To increase accuracy,components are used that are well-designed and relatively large in terms of area and power.To avoid extra cost,calibration can reduce analog complexity,and analog hardware can be replaced with digital hardware.In[1],we described a calibration technique forMUXare connected to the interval detector block,which determines which intervals,Ii(i=1,2,...,16),the sampled value belongs to.The counter records the number of samples for each Ii.The ideal number of samples for each interval can be calculated in advance because the input PDFmust be known.

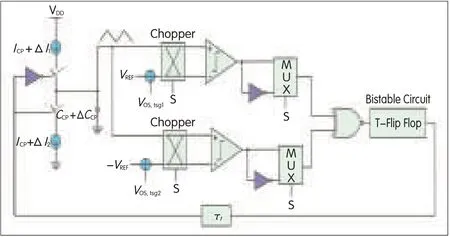
▲Figure 1.Triangular signalgenerator(TSG)circuitwith error sources indicated.

The estimation block in the ADC estimates the voltage errors by comparing the wanted(ideal)nber of samples,Ni,and the recorded number of samples,(the tilde indicates the non-ideal case),for each Ii.The results of the comparison are then used by the trimming block to compensate for static errors.As we outlined in the behavioral-level description in[1],the trimming block can compensate for ADCerrors by adjusting the voltage taps of the resistor ladder.This changes the ADC reference levels generated by the reference-selection block.

3 PDF Generator Circuit

The PDFgenerator is a vital component because it creates a reference signal with a known PDF,which the calibration relies on.Various analog signals might be used for test purposes,but a good candidate in terms of implementation complexity is the ramp function,which can be generated with,for example,a charge pump.Ideally,the ramp signal has a uniform distribution;that is,the PDFhas a constant value because the ramp takes all analog levels with equal probability.For our ADC,we use a triangular signal generator(TSG)(Fig.1)for uniform distribution.(We will return to the choppers and MUXs in Fig.1.)The capacitor,CCP,is charged and discharged sequentially by a pull-up or pull-down current,ICP.Two comparators toggle the direction of the charge pump(up or down)with the help of a decoder and a latch.The overall circuit is a fixed-frequency oscillator.

The resulting triangular wave has amplitude of VREFand a constant PDF.Ideally,the TSG range should be the same as the ADC range,that is,VREF=VR.The signal must be kept in the range[-VR,VR]and should vary linearly with time.Other signal specifications do not need to be taken into account;slope variation,for example,does not affect the PDF distribution.However,in the TSG circuit(Fig.1),some potentially dominating non-ideal effects are mismatch between up and down currents,variation in capacitance,comparator offset,and transition delay.

Of these parameters,the current mismatch,ΔICP,and capacitor mismatch,ΔCCP,only change the slopes of the generated ramps and therefore do not affect the PDF.The offset delay,Vos,tsg,and transition delay,τt,change the upper and lower limits of the voltage across the capacitor.This means there is a deviation from the peak values VREFand-VREF.This variation can be determined from the resolution of the PDFcircuit,and its maximum value is given by

where VLSB,tsgis the voltage of the least-significant bit(LSB)in the TSG circuit.The TSG resolution,ntsg,is

The voltage across the capacitor forms the output of the TSG circuit and is fed to the ADC during calibration.The ratio between the TSG frequency and ADC sampling frequency should be carefully chosen to guarantee a uniform distribution[2],[3].

Assuming the TSG is nonlinear,we can start by looking at first-order,non-linear transfer characteristics.The linearity can be specified by the maximum deviation from a straight line between the two end points,VREFand-VREF.The deviation,η,is normalized with respect to the signal swing and is expressed as a percentage:

whereΔVmaxis the maximum deviation from the straight line.Typically,this deviation is due to limited output impedance of the current sources,and a voltage-dependent capacitance,CCP.To determine the effects of TSG errors on calibration,a behavioral-level model of the TSG is used for simulation.Starting with a 4-bit flash ADC and large comparator offsets(σis approximately 60 mVfor VR=1 V),we run Monte Carlo analyses and calibrate the ADC using equations(4)-(7)in[1].The ADC differential nonlinearity(DNL)is extracted and characterized with respect to the maximum,non-ideal deviation from(4).

The simulation results are shown in Fig.2.The DNLis expressed in LSBs,and refers to a 4-bit converter.DNL should therefore be below 0.5 LSB for full,nominal accuracy.In Fig.2,an 8-bit resolution is indicated.In practical design,the nonlinear behavior of the TSG circuit is not significant,and the nonlinearity as high as four or five percent can be tolerated.

However,for high-resolution converters,a large ntsgis required.In this case,(3)imposes stricter limitations on Vos,tsgandτt,and for each extra bit,we halve the accepted values.The design of a comparator with small offset and low delay could become quite complex,and to avoid this,we introduce a chopping technique that cancels out the effect of the offset values of the TSG comparators[4],[5].

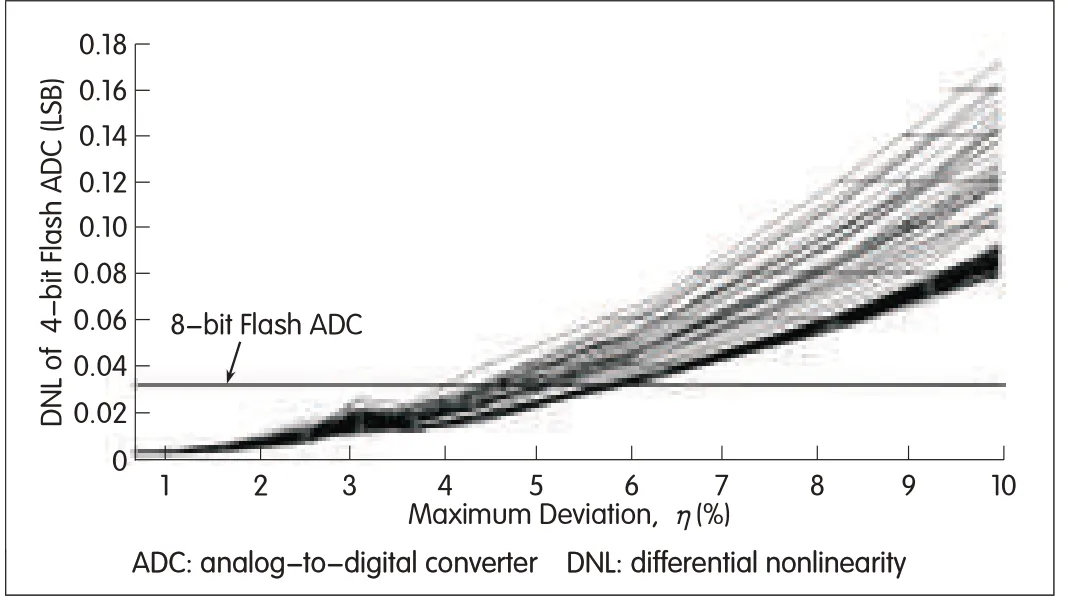
▲Figure 2.DNLof the 4-bit flash ADCversus maximum deviationη for 100 Monte Carlo analyses.

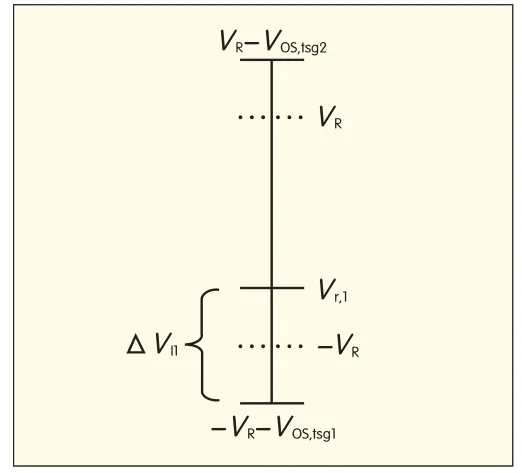
▲Figure 3.Effect of the TSG comparator offset on the reference voltage intervals.

3.1 Chopping

Fig.3 shows the effect of an offset in the lower comparator in the TSG circuit.In this case,the number of samples belonging to the first interval,I1,can be estimated using

whereΔVI1and VFS,including the offset voltages,are the spans of the first voltage interval and the full-scale voltage range,respectively.Replacing these terms with their corresponding values gives

where Vr,1is the ideal reference voltage of the first ADC comparator,VRis the reference voltage,Vos,tsg1is the offset voltage of the bottom comparator,N is the total number of samples,andΔAssumingΔVos,tsgis small,Taylor expansion can be used to approximate(6):

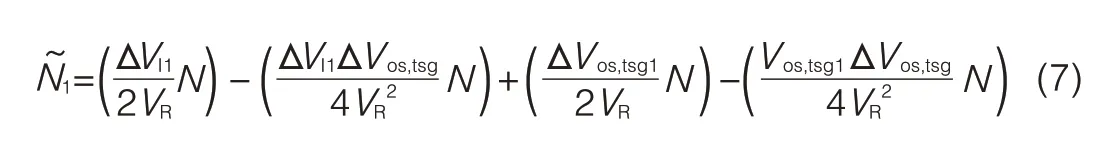
whereΔVI1is the first voltage interval(Fig.3).The last term in(7)is negligible as long as

where VLSBis the LSBvoltage of the ADC.Replacing the value of VLSBin(8)for an n-bit converter,and considering the worst condition,Vos,tsg1=-Vos,tsg2,then

Even for high-resolution converters,(9)dictates that a relatively high offset is tolerable in the TSG comparators.

When the maximum offset is lower than the value estimated in(9),the last term in the Taylor expansion(7)can be ignored.The average value,which is obtained from chopping,is simplified as

where N1,aveis the average value of N1in the two chopping states.The offsets of the TSG comparators are tolerable as long as they are less than the maximum offset defined in(9).

To determine the effects of any TSG comparator offset,a behavioral-level 8-bit flash ADC with full-scale range VR=1 Vis calibrated.All the ADC error sources are set to zero so that only the offset errors of the TSG comparators are introduced.Fig.4(a)shows simulated integral nonlinearities(INLs)and differentialnonlinearities(DNLs)of the converter before chopping.Fig.4(b)shows simulated INLs and DNLs of the converter after chopping.ADC performance degrades significantly as a function of the TSG comparator offsets(Fig.4a).We took the DNL and INLfrom 100 Monte Carlo iterations and saw that by using chopping,the maximum tolerable offset was as high as 80 mVfor VR=1 and n=8.This is a significant improvement using very simple methods.

4 Track-and-Hold

The track-and-hold(T/H)circuit,also called sample-and-hold(S/H)circuit,is an integral part of most ADCs because it makes the converters less sensitive to jitter.In this section,we show how the proposed calibration technique also compensates for the static part of errors introduced by a typical T/H circuit.Such errors include kickback noise,gain,and nonlinearity.The proposed T/H structure(Fig.10)is an active,source-follower-based T/H.It contains input buffers implemented by NMOS source-followers as well as output buffers implemented by PMOSsource-followers.The NMOSdrives the sample-and-hold capacitor,CH,and the PMOSdrives the comparator inputs that form a potentially large capacitive load.

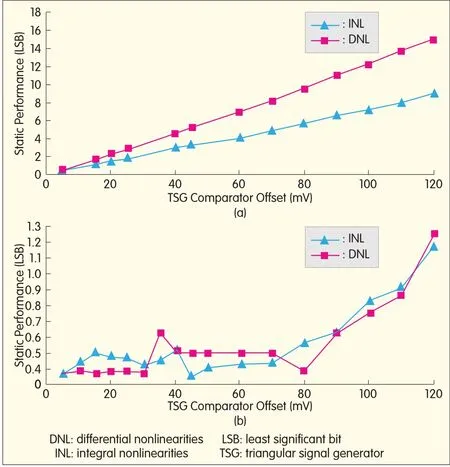
▲Figure 4.INLand DNLof the 8-bitconverter versus TSGcomparator offset(a)before and(b)after chopping.

4.1 Kickback Noise

Kickback noise due to the capacitive coupling from comparator output to input affects both the references and signal inputs.In[1],we observed that by adding trimming switches,some of the kickback noise was suppressed onto the reference ladder.However,a T/Hcircuit with high driving capability(low enough output impedance)is required to diminish kickback on its own output(the comparator inputs).

Calibration relaxes design requirements by compensating for the static part of kickback noise.This can be done by assuming each comparator has zero offset error.The kickback noise on each comparator input is not detrimental unless the input signal is close to the corresponding reference voltage,that is,when the comparator makes a decision.From the point of view of static,kickback noise is deterministic and can be modeled by an equivalent offset voltage at each comparator.However,the amplitude does not depend solely on the input signal;it also depends on its derivative(s).In practice,the amount of kickback noise changes with frequency.To determine the effects of kickback noise in practice,a T/Hcircuit is designed in a 1.2 V,65 nm CMOS process and used in a 4-bit flash ADC.

Fig.5 shows deviation of kickback noise from the average for 15 reference levels.The signal frequency(full-scale sinusoid)is swept,and to isolate kickback noise from other errors—including clock feedthrough(CFT)and charge injection—the sampling switch is bypassed(its drain and source are tied together).Up to about 10 MHz,kickback noise is nearly constant and depends only on the input signal levels.For frequencies higher than 100 MHz,kickback noise amplitude increases significantly.For low frequencies,deviation from the average is nearly constant,which means that the calibration algorithm can calibrate the static part of the kickback noise.For simplicity,we assume the kickback noise for all levels i=1,2,...,2n-1 changes in proportion to the input signallevel,given by

where vk,iis the kickback amplitude,vinis the input signal level andαiandβiare constants.In the first calibration step,the estimated comparator offset i is

where vest1,iis the estimated offset value and Vr,iis the reference level,which can be used as an approximation of the input signal level.vest1,iis added to the reference level by the trimming circuitry[1]and compensates for the offset.The

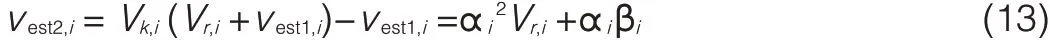
second calibration step gives and the m th calibration step gives

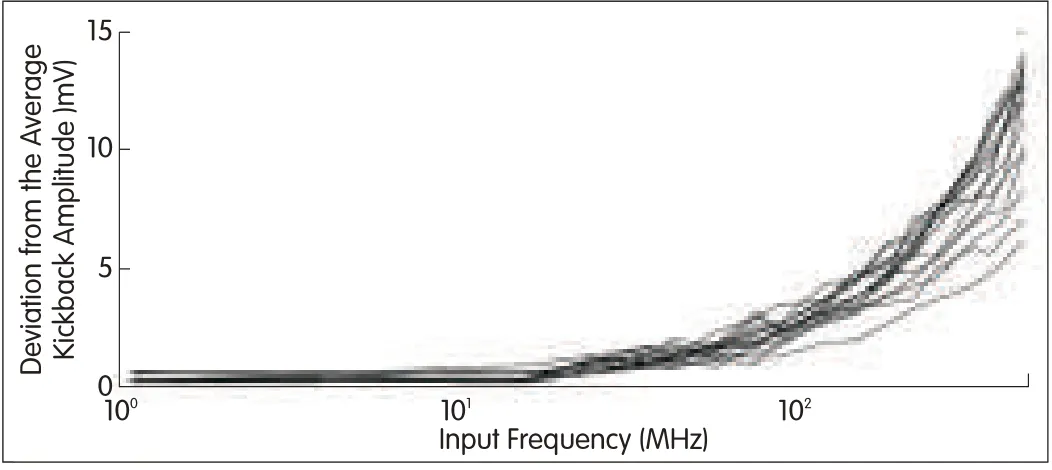
▲Figure 5.Deviation of kickback amplitude from its average versus inputsignalfrequency.

For a nonzero comparator offset,the trip point is shifted from Vr,ito Vr,i-VOS,i,and(14)is modified as

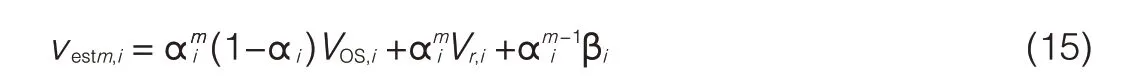
For a typical T/H circuit,we assume thatαiis less than 1 because it is very unlikely the kickback noise is in parity with high input signal levels.This means that the kickback amplitude of the ith comparator is less than the corresponding reference level.In this case,as m increases with calibration iterations,the estimated voltage vestm,iin(15)decreases.The calibration converges and compensates for the static part of the kickback noise.

To verify(15),we examine a 4-bit flash ADC implemented in a 65 nm CMOSprocess with the previously mentioned parameters.To focus solely on the kickback noise,the nominal condition is simulated with zero mismatch.The T/H is omitted,and source impedance is introduced into the input signal generator in order to determine kickback behavior.The ADC response to a full-scale ramp signal is shown in Fig.6.Each ramp corresponds to one calibration step.Before calibration(the first ramp),the ADC suffers DNLerrors and missing codes because of the kickback noise.After seven calibration steps,the algorithm converges and compensates for the kickback noise.

4.2 Gain Errors

Another issue with T/H circuits is gain error.Some effort is required to design a buffer with acceptable gain variations,especially in fine-line CMOStechnologies where process variations can substantially affect the open-loop buffer gain.Using the proposed technique,gain error can be calibrated because the effect of the gain error can be described by a set of comparator offset voltages.The corresponding reference and trimming voltages are then rearranged to compensate for the gain error.The T/H gain error in the calibration algorithm generates equivalent offset errors given by

whereγis the gain error of the T/H circuit.

The T/H circuit is used in a 4-bit flash ADC,and behavioral-level models are used so that the comparators can isolate the gain error.Fig.7 shows the arrangement of the reference voltages of the ADCduring calibration.At first,the reference levels are in their ideal positions.As the calibration proceeds,these reference levels are pushed towards the range of the T/H output.The original ADCrange is shown by the dotted line,and the reference levels are pushed and distributed inside the signal range.Each 0.2μs corresponds to one calibration step.

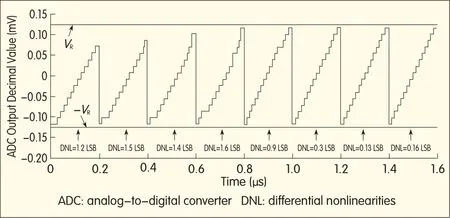
▲Figure 6.Transistor-levelsimulations showing calibration steps and compensation for T/Hkickback errors.

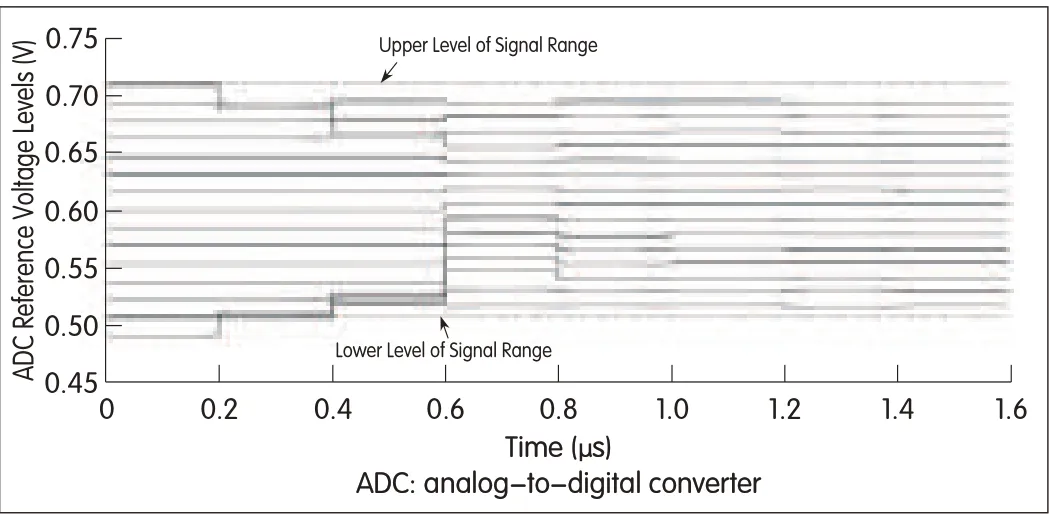
▲Figure 7.Calibration steps showing the compensation for T/Hgain error.

4.3 Distortion and Nonlinearity

Dominant T/H errors include distortion that are due to nonlinearity of the sample-and-hold capacitor.Switch-on resistance is another dominant T/H error.The calibration here is not intended to compensate for any dynamic nonlinear errors.For static errors,the input and output relationship can be described by a relatively well-defined polynomial:

The T/H static nonlinearity can be calibrated as long as the aicoefficients are smallenough.To determine the effect of moderate distortion,the T/H is used in an 8-bit flash ADC.Behavioral-level comparators are used,and the sampling switch is bypassed to avoid kickback.The effect of distortion can then be analyzed in isolation.INLbefore calibration in Fig.8(a)has a maximum absolute value of about 2 LSB.INL after calibration in Fig.8(b)and is improved to about 0.15 LSB.

5 Implementation

Fig.9 shows the proposed calibration system,and an implementation of the calibration algorithm has already been presented in[1].The ADC input is connected to the TSG circuit(PDFgenerator)in calibration mode[1].The 2n-1 comparators produce a thermometer code so that an ADC level is represented by a set of r consecutive 1s at the bottom and s consecutive 0s at the top.The MUXselects a set of 16 comparators and feeds their outputs to the interval-detector block.This block then locates the input signal in the different voltage intervals and produces a 1-of-16(walking-one)code at the block’s output,which indicates the corresponding code value.

For smallerrors,the voltage intervals do not overlap[1],and in the thermometer code,there are normal transitions between 1 and 0,that is,no sparkle errors.However,for large offset errors,the intervals overlap,and this is detected and compensated for by the interval-detector block.

The outputs of the interval detector are applied to the estimation block,which contains an array of counters that record the number of samples belonging to each interval.All offset values are then estimated according to the procedure given in the behavioral-level description of the algorithm[1].The estimated offset values are stored in a 16-word RAM.Each word represents the offset of a comparator in the chosen set.The trimming block in Fig.9 reads the RAM and performs encoding to reduce the word length.It then stores the result in registers that contain 2n-1 words that represent the offset for each comparator.The register word lengths typically depend on the maximum comparator offset because larger offsets result in longer word lengths.

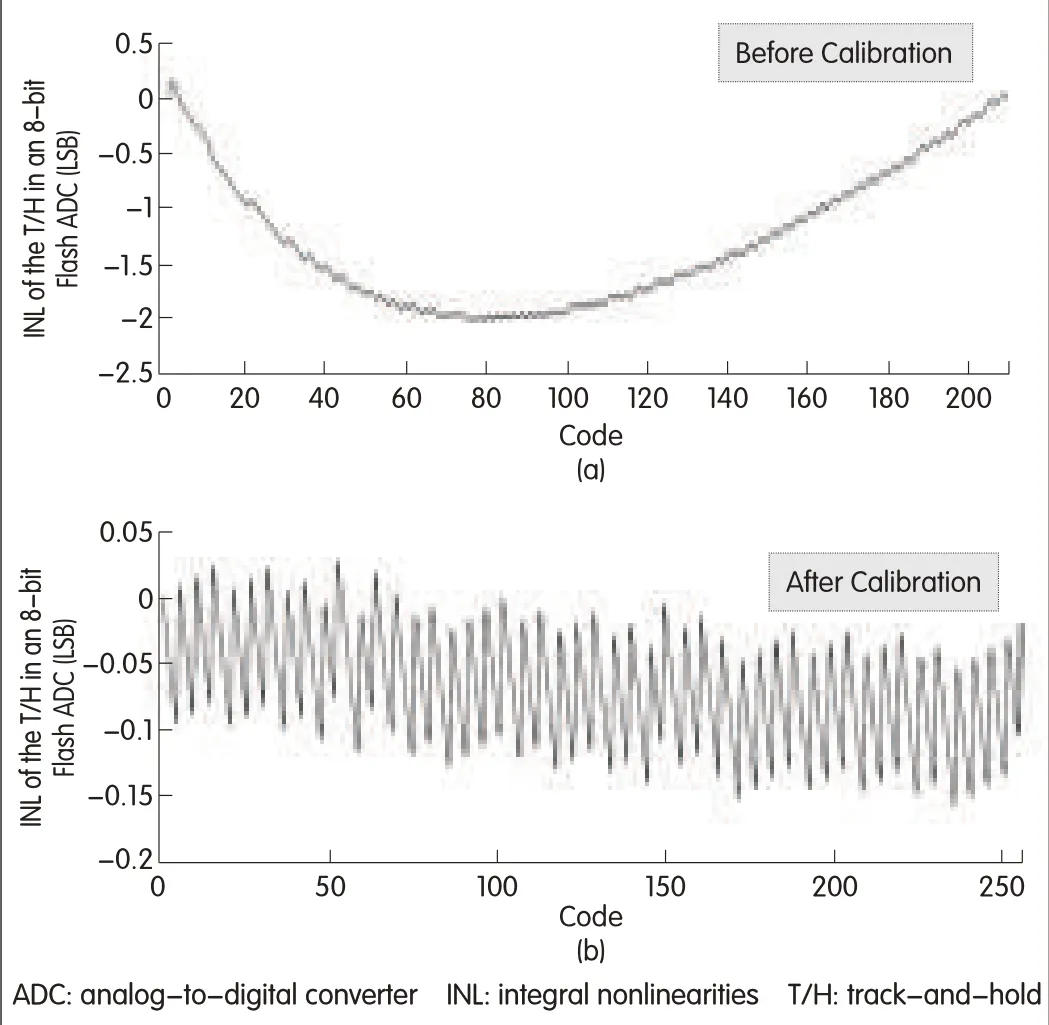
▲Figure 8.INLof an 8-bitflash converter using a T/Hcircuit(a)before and(b)after calibration.

Each register defines the select lines,which in turn control the analog multiplexers(AMUXs)in the reference generator.There is one AMUXassigned to each comparator.Each MUX can select from a batch of reference voltage taps on the resistor ladder.Each input provides a fractional LSB so that a fine voltage step can be added to or subtracted from the MUX output.This output is then used as the new reference voltage for the corresponding comparator.

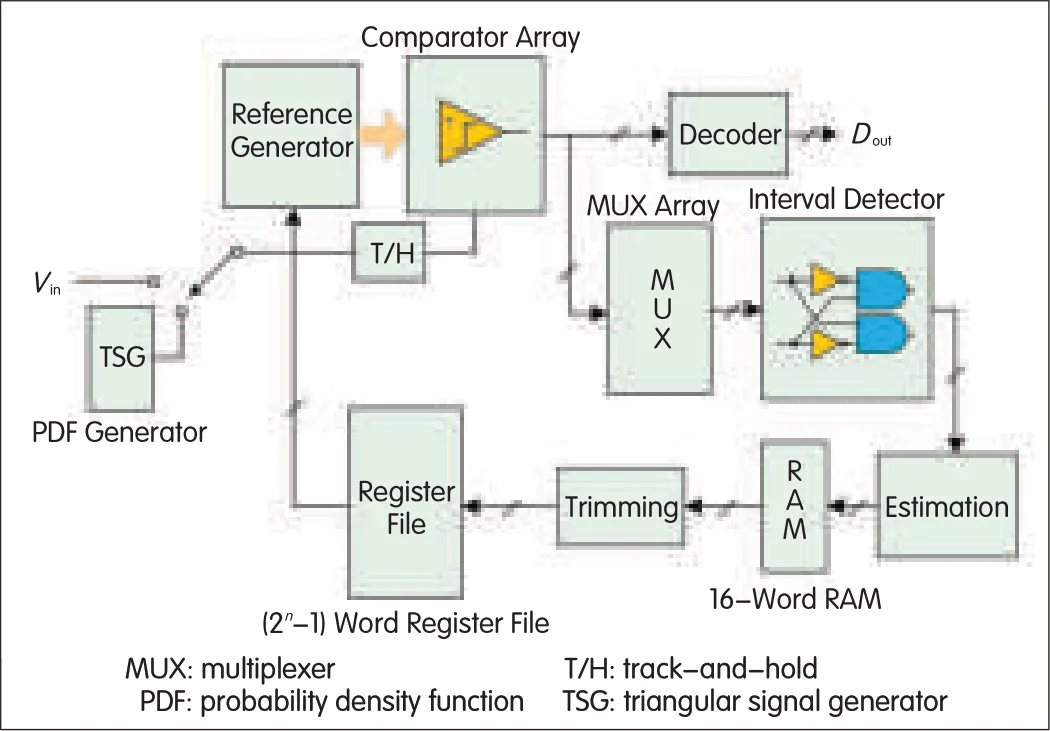
▲Figure 9.Proposed calibration system.

5.1 Complexity

The analog switch area of the AMUXarray is proportionalto

where n is the resolution of the converter,Vos,maxis the maximum static error amplitude covered by the calibration algorithm,VLSBis the LSBvoltage,M is the number of fine sub-LSB steps,and AATGis the area of each TG.Inserting VLSB=2VR/2ninto(18)results in

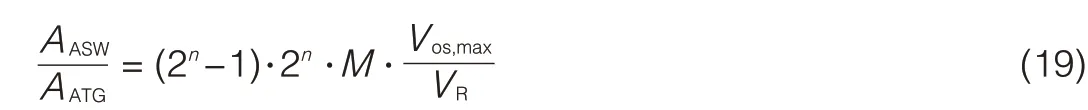
The same equation can be used for the decoder part:the digital MUX(DMUX)array at the output of the comparators is implemented using unity TGs.In this case,the area can be approximated using

where ADTGis the area of the unity TG.The register file

contains 2n-1 words,and each represents the selected lines of the corresponding AMUX.So,similar to(19),we get

where ALis the area of a typical latch used in the register file.According to(19)-(21),the areas of the AMUX,DMUX,and register file grow exponentially in relation to resolution n.The size of the remaining calibration blocks is proportional to the resolution because of the segmented approach[1].With the segmented approach,a considerable amount of calibration hardware grows linearly,rather than exponentially,in relation to converter resolution.

The size of the calibration blocks can be ordered according to the size of the total ADC area:all-digital estimation block,RAM,and trimming block(33%);decoder part of the AMUX array(10%);analog switches of the AMUXarray(6%);TSG circuit(2%);register file(2%);and DMUXarray(1%).This accounts for approximately half the total area of the ADC,which is 0.25 mm2.Unlike the analog area,the calibration area does not scale exponentially as higher resolutions are attained.Using calibration,the analog comparator area can be kept fairly low and,most importantly,analog complexity can be reduced by using standard digital cells.

6 Simulation Results

As a proof-of-concept,a single-ended,5-bit flash ADC is designed in the same 1.2 V,65 nm CMOSprocess used previously.The ADC range is from 475 to 725 mV,which allows a full range of 250 mV(related to the single-ended signal).Fig.10 shows the T/H circuit where a boot-strapped sample switch is used to enhance performance[6].A replica of the input buffer injects the test signal,Vtest,during calibration.Atransmission gate(M3 and M4)is used as a switch to inject the test signal.The gate can be small;in this design it is 25 times smaller than the sample switch,Msw,because the test signal is typically low-frequency.Therefore,the additional parasitic capacitance is small,and the dynamic performance of the T/H remains relatively unaffected.The T/H circuit has a gain loss of approximately-1.7 d B.

Fig.11 shows the ADC reference generator circuit adopted from[7].Areplica of the T/H circuit is used to match the common-mode level of the reference generator with the input signal.A version of the T/H,scaled down 40 times,is used.Corner and Monte Carlo analyses show that the replica matches the original T/H wellwithin one LSB.Any residual errors due to the mismatch are,however,compensated for during calibration.

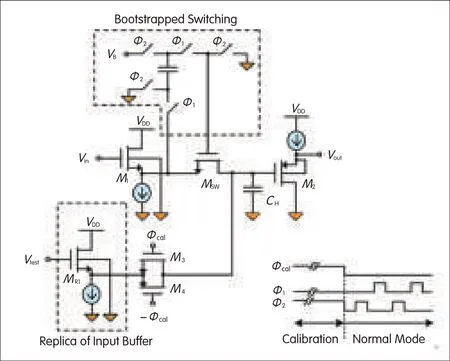
▲Figure 10.T/Hcircuitand injection of the test signal.

The test signalis generated using the TSG circuit in Fig.1.The reference current,ICP,is about 250 nA,and the TSG capacitor is 1 p F.Acomparator with relatively smalloffset and very low kickback is chosen[8].This comparator is power-hungry and slow;it is only used in calibration mode and powered down during normal operation.The TSG comparators have an offset of about 7 mV.The resulting test signal has tolerable nonlinearity of about 1%(Fig.2).

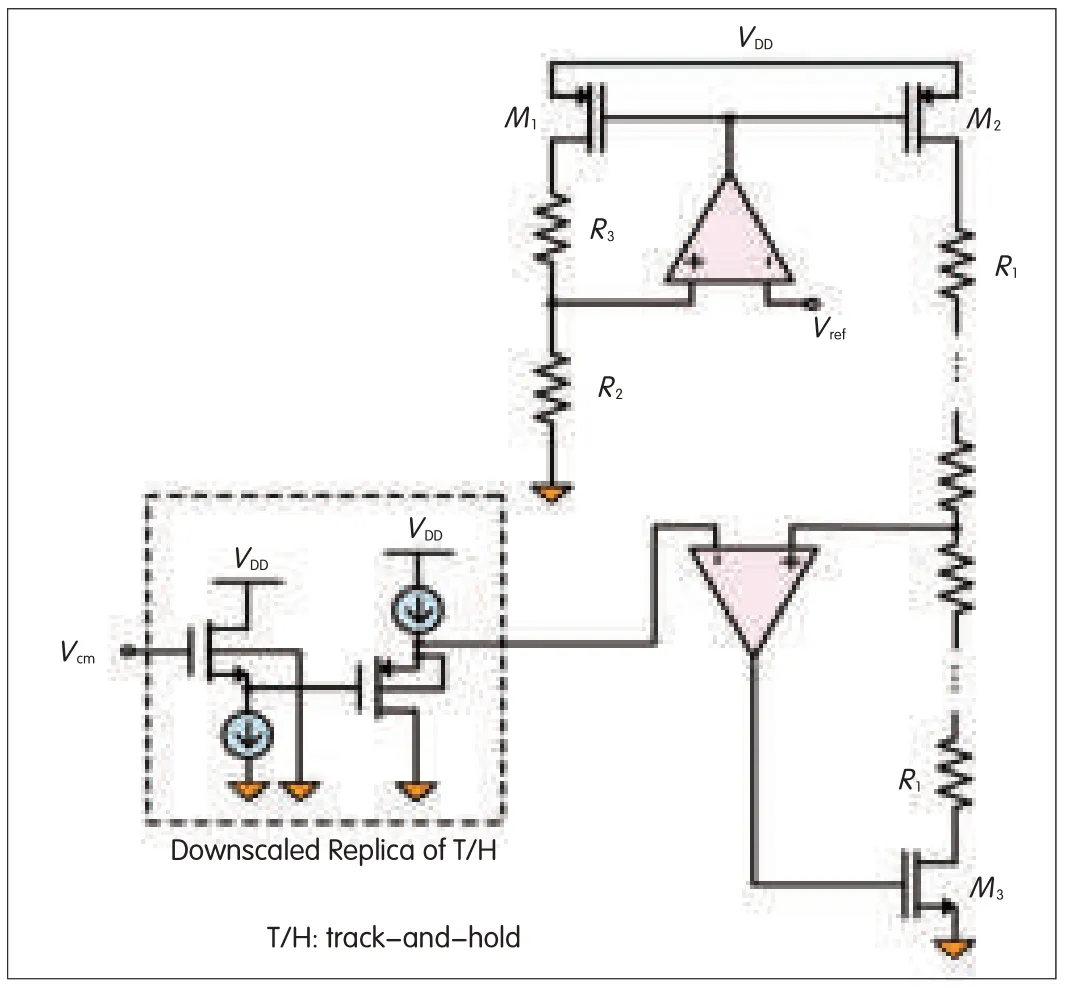
▲Figure 11.Reference generator circuit with downscaled replica of the T/Hcircuit.

The trimming circuit is implemented using a 32-to-1 AMUX array.A set of transmission gates are controlled by 5-bit words.Each TG is about ten times larger than the minimum-sized TG,and there are three fine LSBsteps.The core flash ADC comparators have an input-referred offset of approximately 15 mVand are clocked at 1 GHz;that is,the ADC operating frequency is 1 GHz.Then,ADCis calibrated using a test signal with a ramp frequency of about 500 kHz.

To save simulation time,each step of the calibration is completed with a relatively low number of samples(approximately 2000).The simulated DNL and INL before calibration are shown in Fig.12(a)and(b),and the results after 16 calibration steps,are shown in Fig.12(c)and(d).The DNL is reduced from 2.5 LSB to about 0.7 LSB,and the INL is reduced from 1.6 LSB to about 0.6 LSB.

The proposed technique is effective in calibrating important errors in the structure of the flash ADC(Fig.12).We chose a low number of samples for each calibration cycle in order to decrease the simulation time and prove the effectiveness of the calibration method.Further improvement in DNL and INL in the ADC can be achieved by using a higher number of samples in each calibration cycle.This would,however,affect the setup time of the system,and there would be a trade-off between obtainable resolution and calibration time.In this work,only a single-shot simulation result has been given.In the behavioral-level simulation results in[1,Fig.8],98%of cases were successfulusing an 8-bit ADC with 25 mV comparator offset.In this simulation,using a 5-bit ADC with a 15 mVcomparator offset gives a higher rate of success.

7 Conclusion

The ADC architecture and calibration technique were described in[1],and this follow-up paper focuses on additional errors that arise as a result of moving towards transistor-level implementation.We show how the calibration technique handles errors that arise when different blocks of the flash ADC are implemented.The chosen implementations have a minimally detrimental effect on the ADC because they do not change the comparators.A triangular waveform is generated by a PDFcircuit in which the comparator offsets could cause significant errors that affect calibration.However,using chopping,a large offset value is tolerable,and analog complexity can further be reduced.

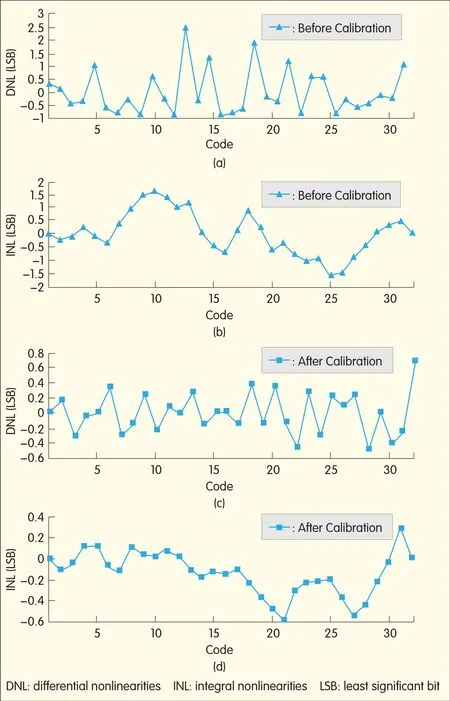
▲Figure 12.(a)DNLand(b)INLof the flash ADCbefore calibration,and(c)DNLand(d)INLafter calibration.

Simulation results for different sub-blocks have also been given.As a proof of concept,a full transistor-level simulation of a 5-bit,0.25 mm2,1 GHz flash ADC in a 65 nm CMOS process was performed.Simulation results show that DNL improved from 2.5 LSB to about 0.7 LSB after calibration,and INL improved from 1.6 LSB to about 0.6 LSB after calibration.We have described how Analog complexity can be traded off against digital complexity and how obtainable resolution can be traded off against system setup and calibration time.