盛秀蘭, 艾 堯, 吳宏偉

(1.東南大學(xué)數(shù)學(xué)系 江蘇南京210096;2.江蘇廣播電視大學(xué)公共課教學(xué)部 江蘇南京210036)

一個類似Burgers方程的數(shù)值解

盛秀蘭1,2, 艾 堯1, 吳宏偉1

(1.東南大學(xué)數(shù)學(xué)系 江蘇南京210096;2.江蘇廣播電視大學(xué)公共課教學(xué)部 江蘇南京210036)

研究了一個類似Burgers方程的初邊值問題的有限差分方法.基于Crank-Nicolson方法,建立了一個兩層線性化隱式差分格式,討論了差分格式的可解性.利用離散能量估計方法證明了差分解在最大模意義下關(guān)于時間和空間的二階收斂性,并用數(shù)值算例驗(yàn)證了理論分析結(jié)果.

類似Burgers方程;隱式差分格式;收斂性;離散能量估計

0 引言

考慮初邊值問題[1]:

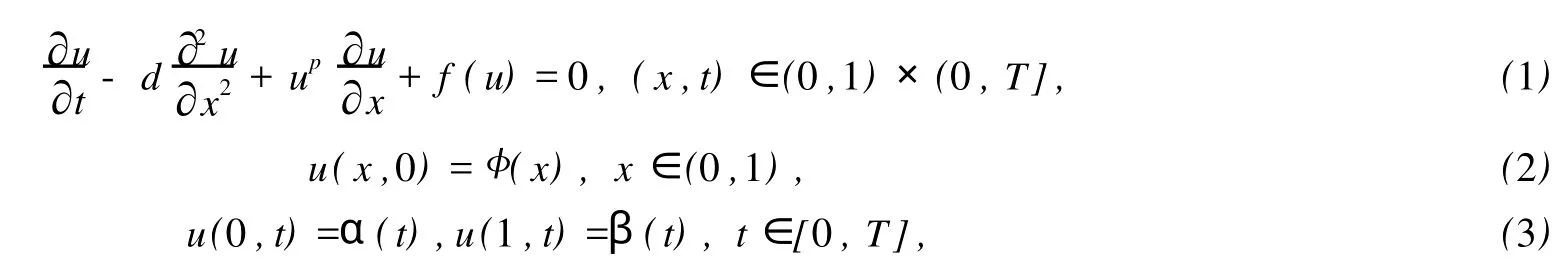
其中,p=1,2,d>0為粘性常數(shù),f(u)是非線性函數(shù),φ(x),α(t),β(t)為已知光滑函數(shù),且滿足相容性條件.

當(dāng)p=1且f(u)≡0時,方程(1)成為著名的Burgers方程,有很多文獻(xiàn)研究了該問題的數(shù)值解法.可以通過Hop f-Cole變換將方程化為一個標(biāo)準(zhǔn)的熱方程,然后用高階差分格式求解[2-4].但是當(dāng)f(u)≠0時,此方法不再適用.文[5]研究了當(dāng)f(u)≡0時保持能量守恒的差分格式,但當(dāng)f(u)非零時能量不再守恒.文[6]給出了一個線性化的差分格式,該格式的截斷誤差是O(τ+h2),但文中沒有給出理論分析結(jié)果.

通過分析以上文獻(xiàn),正如[3]指出的,當(dāng)p=1且f(u)=0,如果對方程(1)直接用差分逼近,得到的線性化格式一般關(guān)于時間的精度是1階的,要得到關(guān)于時間是2階的格式,如用Crank-Nicolson格式,通常格式是非線性的或者是3層以上格式.其原因主要是非線性項(xiàng)uux的線性化離散問題.當(dāng)帶有非線性強(qiáng)迫項(xiàng)后,要構(gòu)造關(guān)于時間2階收斂的線性化兩層格式顯得更為困難.

本文研究當(dāng)p=2時初邊值問題(1)～(3)的線性化差分解法.構(gòu)造了一個關(guān)于時間和空間2階收斂的線性化兩層差分格式.在處理非線性項(xiàng)f(u)的時候,采用與文獻(xiàn)[11]類似的方法,而對非線性項(xiàng)u2ux的逼近,提出了一種新的離散方法.證明了差分格式解的存在唯一性和收斂性.給出了差分格式的解在離散最大模意義下收斂階數(shù)為O(τ2+h2).最后給出了兩個數(shù)值算例,計算結(jié)果顯示本文提出的方法是有效的.

本文假設(shè):

H1問題(1)～(3)存在唯一光滑解,且存在常數(shù)C0,使得對有

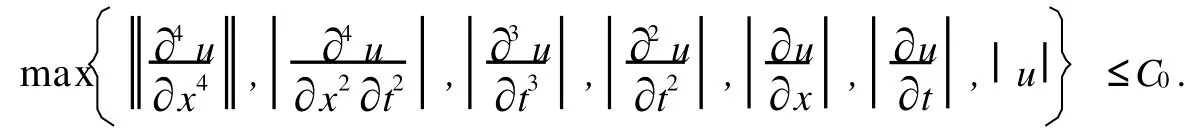
H2函數(shù)f二階可導(dǎo),且存在正常數(shù)C1,δ,使得當(dāng),有

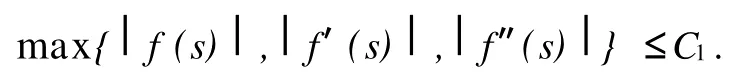
1 記號及差分格式

取正整數(shù)m,n,記h=1/m,τ=T/n,xi=ih,0≤i≤m,tk=τk,0≤k≤n.定義Ωh={xi|0≤i≤={(xi,tk)|0≤i≤m,0≤k≤n}.設(shè){|0≤i≤m,0≤k≤n}為Ωhτ上的網(wǎng)格函數(shù),引進(jìn)記號:

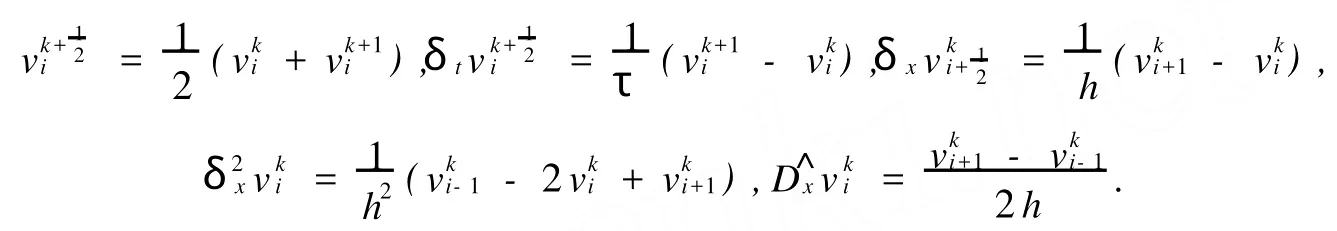
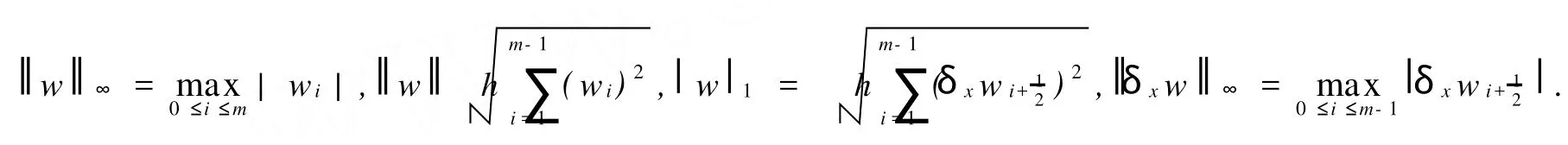
我們構(gòu)造初邊值問題(1)～(3)的差分格式為:

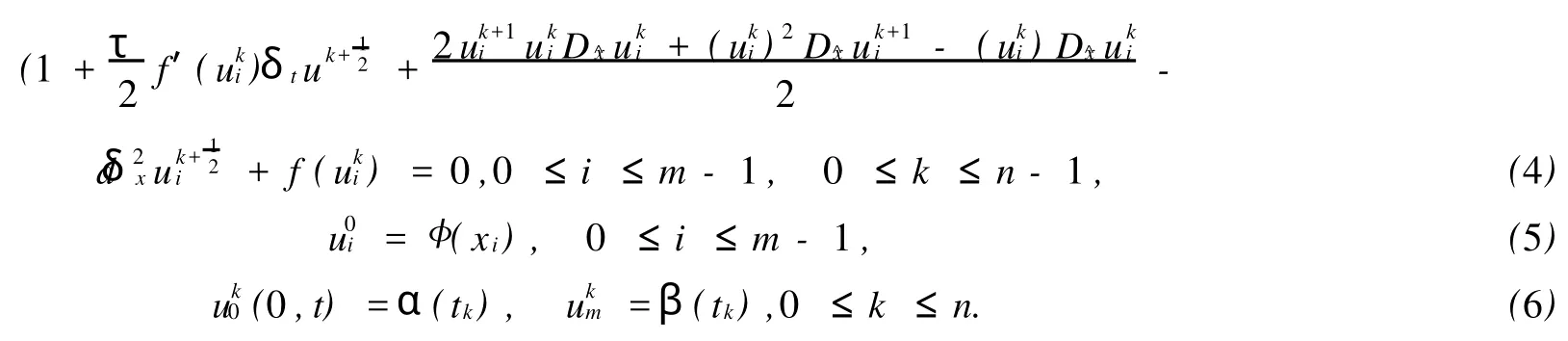
差分格式(4)～(6)是一個兩層線性化的差分格式,對每一固定的時間層k,差分方程的系數(shù)矩陣是3對角矩陣,可以用追趕法求解.

2 差分格式的可解性和收斂性

引理1[12-13]設(shè)v,w∈Vh,則有

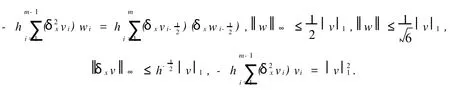
下面的引理2是離散非線性項(xiàng)u2ux的關(guān)鍵.

引理2設(shè)函數(shù)u(t),v(t),w(t)∈C2[0,T],記.則

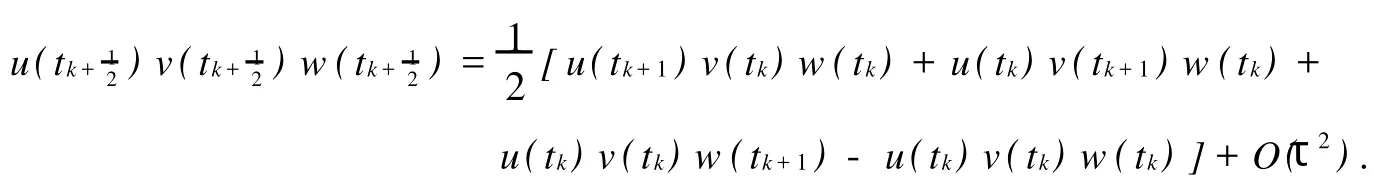
證明記p(t)=(uvw)(t),則由Taylor展開及向前差商得

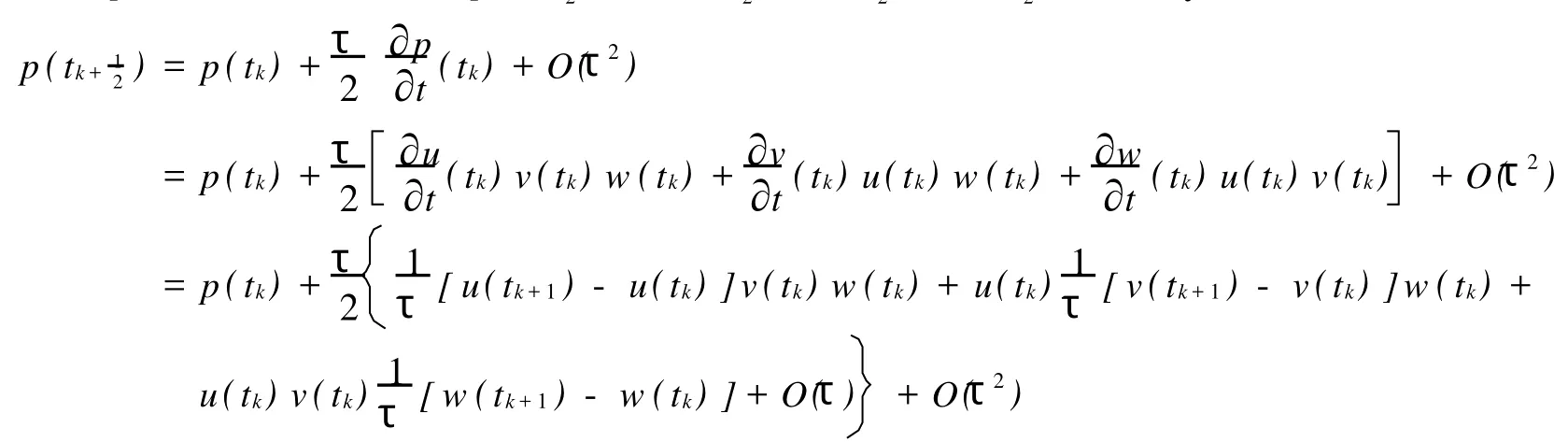
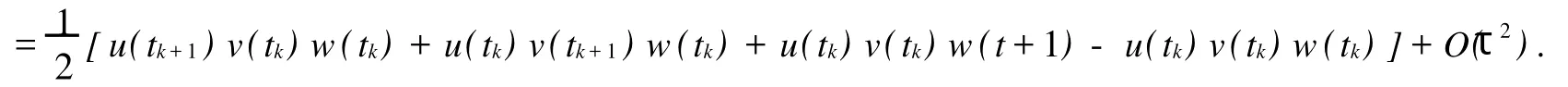
引理2證畢.

利用引理1和引理2以及能量估計和數(shù)學(xué)歸納法,可以得到下面的收斂性估計.

定理1設(shè)u(xi,tk)是問題(1)～(3)的解,滿足差分方程(4)～(6),記,如果φ(x)∈ C[0,1],且存在常數(shù)C0>0,使得,則當(dāng)h,τ充分小且時,有

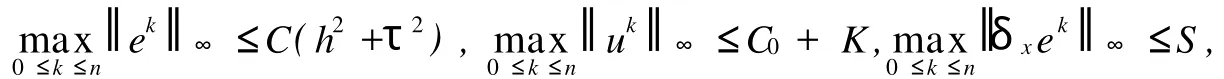
其中,C>0,K>0,S>0是與h,τ無關(guān)的常數(shù).

由定理1可知,當(dāng)步長h,τ充分小時,對固定的k,差分格式(4)～(6)的系數(shù)矩陣嚴(yán)格對角占優(yōu),因此有下面的結(jié)論.

定理2當(dāng)步長h,τ充分小,差分格式(4)～(6)存在唯一解.

3 數(shù)值試驗(yàn)

利用差分格式(4)～(6)計算2個實(shí)例,計算結(jié)果見表1和表2.

例1

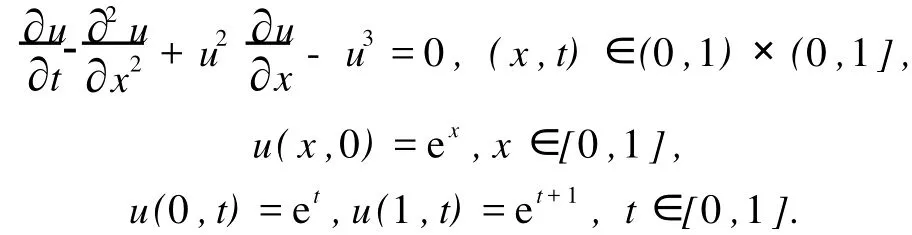
該問題的精確解為ex+1.

例2

表1 例1的不同步長下的誤差和收斂階數(shù)Tab.1 Errorsandconvergencerateaboutthefirstexample

表2 例2的不同步長下的誤差和收斂階數(shù)Tab.2 Errorsandconvergencerateaboutthesecondexample

[1] Bülent S,˙Idris D.A numerical study of the Burgers’equation[J].J Franklin Institute,2008,345(4):328-348.

[2] Brander O,Hedenfalk J.A new formulation of the general solution to Burgers’equation[J].Wave Motion,1998,28 (4):319-332.

[3] Liao Wenyuan.An imp licit fourth-order compact finite difference scheme fo r one-dimensional Burgers’equation[J].App l Math Comput,2008,206(2):755-764.

[4] Yousuf M.On the classof high order time stepping scheme based on Padé’s app roximations for the numerical solution of Burgers’equation[J].App l Math Comput,2008,205(1):442-453.

[5] Anguelov R,Djoko J K,Lubuma JM S.Energy p roperties p reserving schemes fo r Burgers equation[J].Numer M ethods Partial Differential Equations,2008,24(1):41-59.

[6] Kutluay S,Esen A.A linearized numerical scheme for Burgers-like equations[J].App l Math Comput,2004,156(2): 295-305.

[7] Djoko J K.On the long-time stability of a backward Euler scheme fo r Burgers’equation w ith polynomial force[J].Numer Methods Partial Differential Equations,2008,24(6):1371-1387.

[8] Lewandow ski J L V.A markermethod for the solution of the damped Burgers’equation[J].Numer Methods Partial Differential Equations,2006,22(1):48-68.

[9] 孔令江,張超英,譚惠麗,等.用格子Boltzmann方法模擬kdv-Burgers方程的激波解[J].廣西師范大學(xué)學(xué)報:自然科學(xué)版,2003,21(4):1-4.

[10] 洪寶劍,盧殿臣,張大珩.帶強(qiáng)迫項(xiàng)變系數(shù)組合kdv-Burgers方程的顯式精確解[J].廣西師范大學(xué)學(xué)報:自然科學(xué)版, 2007,25(1):17-20.

[11] 吳宏偉.二維半線性反應(yīng)擴(kuò)散方程的交替方向隱格式[J].計算數(shù)學(xué),2008,30(4):349-360.

[12] 孫志忠.偏微分方程數(shù)值解[M].北京:科學(xué)出版社,2004.

[13] Zhou Yulin.App lication of Discrete Functional Analysis to the Finite Difference Method[M].Beijing:International Academic Publishers,1990.

Numerical Solution of a Burgers-like Equation

SHENG Xiu-lan1,2, A I Yao1, WU Hong-w ei1
(1.Department of M athem atics,Southeast University,N anjing 210096,China; 2.D ivision of Public Course,Jiangsu Radio and TV University,N anjing 210036,China)

A second-order finite difference scheme for a Burgers-like equation is p roposed and analyzed.The scheme constructed is a double-deck linearized scheme that can be solved easily by Thomas’algo rithm.The solvability of difference scheme is obtained.It is show n that the difference scheme is convergent in maxim um no rm.The convergence o rder is second-o rder in bo th space and time.Some numerical experiments are conducted to illustrate the theoretical results of the p resented method.

Burgers-like equation;imp licit difference scheme;convergence;discrete energy estimate

O 241.82

A

1671-6841(2010)03-0023-04

2009-11-25

國家自然科學(xué)基金資助項(xiàng)目,編號10871044.

盛秀蘭(1976-),女,講師,主要從事微分方程數(shù)值解研究,E-mail:113525336@qq.com.