不確定時(shí)滯脈沖切換系統(tǒng)的保性能控制
毛北行, 慕小武, 卜春霞
(1.鄭州航空工業(yè)管理學(xué)院數(shù)理系 河南鄭州450015;2.鄭州大學(xué)數(shù)學(xué)系 河南鄭州450001)
不確定時(shí)滯脈沖切換系統(tǒng)的保性能控制
毛北行1, 慕小武2, 卜春霞2
(1.鄭州航空工業(yè)管理學(xué)院數(shù)理系 河南鄭州450015;2.鄭州大學(xué)數(shù)學(xué)系 河南鄭州450001)
研究了一類參數(shù)不確定性和定常時(shí)滯的連續(xù)的脈沖切換系統(tǒng)在任意切換下的保性能控制問題.利用Lyapunov穩(wěn)定性理論與線性矩陣不等式方法,給出了連續(xù)的脈沖切換系統(tǒng)的保性能控制器存在的充分條件,并把這個(gè)條件轉(zhuǎn)化為一個(gè)線性矩陣不等式,便于實(shí)現(xiàn).
脈沖切換系統(tǒng);保性能控制;時(shí)滯
0 引言
切換系統(tǒng)是一類重要的混雜系統(tǒng),它是由一系列子系統(tǒng)和一定的切換規(guī)則構(gòu)成,其中的子系統(tǒng)可能是穩(wěn)定的,也可能是不穩(wěn)定的,切換系統(tǒng)具有這樣的性質(zhì):既使每一個(gè)子系統(tǒng)都是不穩(wěn)定的,通過構(gòu)造切換規(guī)則,也可以保證系統(tǒng)的穩(wěn)定性,反之,既使每一個(gè)子系統(tǒng)穩(wěn)定,切換規(guī)則選得不合適,系統(tǒng)也可能不穩(wěn)定.切換系統(tǒng)已經(jīng)引起了控制界的廣泛關(guān)注并且已取得了很多成果[1-4].另一方面,脈沖現(xiàn)象普遍存在于工業(yè)生產(chǎn)中,近年來,脈沖動(dòng)態(tài)系統(tǒng)的穩(wěn)定性問題已經(jīng)存在較多成果.文獻(xiàn)[5]應(yīng)用Lyapunov函數(shù)直接研究了一類脈沖切換系統(tǒng)的魯棒指數(shù)穩(wěn)定性問題.文獻(xiàn)[6]利用Lyapunov函數(shù)研究了一類擾動(dòng)的脈沖切換系統(tǒng)的魯棒H∞問題,但兩者均沒有考慮時(shí)滯和不確定性.文獻(xiàn)[7]針對(duì)具有不確定性和狀態(tài)滯后的連續(xù)系統(tǒng),提出了無記憶狀態(tài)反饋和靜態(tài)輸出反饋保性能控制,給出了保性能控制律存在的充分條件.
不確定性和時(shí)滯是引起系統(tǒng)不穩(wěn)定和性質(zhì)變壞的主要因素,因此不確定性和時(shí)滯對(duì)系統(tǒng)的控制性能產(chǎn)生巨大影響.文獻(xiàn)[8]研究了具有時(shí)滯的不確定離散脈沖切換系統(tǒng)的保性能控制問題,但討論的是離散系統(tǒng),本文將對(duì)具有時(shí)滯和不確定性的連續(xù)脈沖切換系統(tǒng)的保性能控制問題進(jìn)行研究,給出了系統(tǒng)存在保性能控制器的充分條件.
1 問題描述
考慮以下具有定常時(shí)滯和不確定性的連續(xù)脈沖切換系統(tǒng)
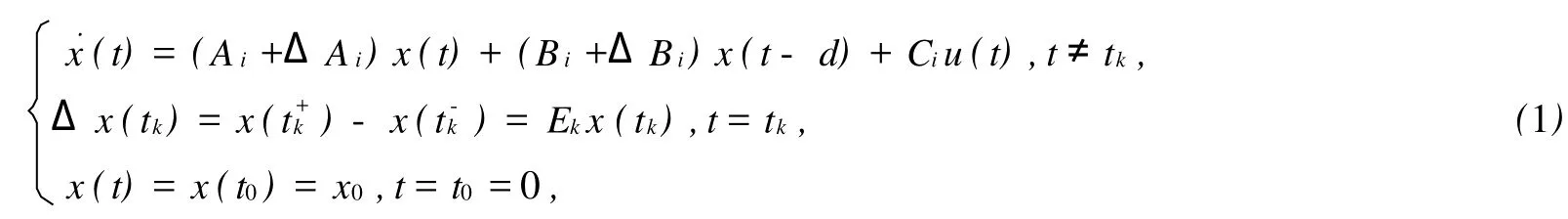
其中,x(t)∈Rn是狀態(tài)向量;u(t)∈Rm是控制輸入向量;Δx(t)是切換脈沖;Ek是脈沖矩陣,只與切換前后2個(gè)子系統(tǒng)有關(guān),與切換時(shí)刻無關(guān),當(dāng)切換規(guī)則一定,它是一系列實(shí)常矩陣,
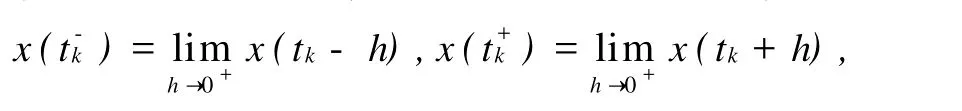
其中,Ai,Bi,Ci是常數(shù)矩陣,ΔAi,ΔBi是未知矩陣,且假設(shè)其具有形式

其中,Mi,Fi,Hi是已知適當(dāng)維數(shù)的實(shí)矩陣,不確定參數(shù)矩陣Γi是滿足ΓTiΓi 系統(tǒng)(1)的性能指標(biāo)定義為 其中,Qi,Ri是給定的對(duì)稱正定矩陣. 反饋控制律為 其中,Ki是待定的反饋增益矩陣,閉環(huán)系統(tǒng)為 問題表述如下:對(duì)系統(tǒng)(1),在性能指標(biāo)(3)的要求下,設(shè)計(jì)一個(gè)無記憶狀態(tài)反饋控制律(4),對(duì)所有允許的不確定性,閉環(huán)(5)是漸近穩(wěn)定的,且存在J*>0使得性能指標(biāo)J≤J*. 引理1 給定適當(dāng)維數(shù)的矩陣Y,D和E,F,則Y+D FE+ETFTDT<0對(duì)所有滿足FFT≤I的矩陣F成立,當(dāng)且僅當(dāng)存在一個(gè)常數(shù)λ>0,使得Y+λDDT+λ-1ETE<0. 引理2(Schur補(bǔ)引理) 設(shè)A,B,C為適當(dāng)維數(shù)的矩陣,則下面3個(gè)式子等價(jià): 定理1若存在正定矩陣Pi,滿足矩陣不等式 其中, 則對(duì)應(yīng)閉環(huán)性能指標(biāo),J≤J*=xT0Pi0x0,且形如(4)的控制律是(1)的一個(gè)狀態(tài)反饋保性能控制律.證明 定義指標(biāo)函數(shù):ξ(t)=[ξ1,…,ξN]T, 其中, 由不等式(6)得 當(dāng)t=tk時(shí),不妨設(shè)系統(tǒng)從子系統(tǒng)i切換到j(luò), 由不等式(7),得 從而對(duì)所有允許的不確定性,閉環(huán)(5)是漸近穩(wěn)定的.下面求(1)的性能上界.由(8)兩邊求積分,得 其中, 則對(duì)應(yīng)的閉環(huán)性能指標(biāo)J≤J*=xT0Pi0x0,且u(t)=WiX-1ix(t)是系統(tǒng)的一個(gè)狀態(tài)反饋保性能控制律. 證明利用Schur補(bǔ)引理2,矩陣不等式(6)可以改寫為 將不等式兩邊分別左乘、右乘以矩陣diag{P-1i,I,I,I,I},并記 即可得矩陣不等式(9). 本文研究了連續(xù)的不確定時(shí)滯脈沖切換系統(tǒng)的保性能控制問題,得到系統(tǒng)存在保性能控制器存在的一個(gè)充分條件,求出了保性能控制律和性能上界,并最終得到一個(gè)線性的矩陣不等式.本文同時(shí)考慮了不確定和時(shí)滯因素帶來的影響,結(jié)果更具一般性. 參考文獻(xiàn): [1] Libezon D,Mo rse A S.Basic p roblem s in stability and design of sw itched systems[J].IEEE Control System s Magazine, 1999,19(5):59-70. [2] Daafouz J,Riedinger P,Iung C.Stability analysis and control synthesis fo r sw itched systems:a sw itched Lyapunov function app roach[J].IEEE Transaction on Automatic Control,2002,47(11):1302-1310. [3] Lee S H,Kim T H,Lim J T.A new stability analysis of sw itched systems[J].Automatic,2000,36(6):917-922. [4] Rober T S,Kumputi SN,Oliver M.A result on common quadratic Lyapunov functions[J].IEEE Transactionson Automatic Control,2003,48(1):110-113. [5] 許弘雷,劉新芝.一類受擾動(dòng)脈沖切換系統(tǒng)魯棒指數(shù)穩(wěn)定[J].控制理論與應(yīng)用,2004,23(11):14-16. [6] 張紅濤,劉新芝.關(guān)于一類脈沖切換系統(tǒng)的魯棒控制[J].控制理論與應(yīng)用,2004,21(2):261-266. [7] 俞立.不確定離散系統(tǒng)的最優(yōu)保性能控制[J].控制理論與應(yīng)用,1999,16(5):639-642. [8] 秦婧文,高睿,劉新芝.具有時(shí)滯的不確定離散脈沖切換系統(tǒng)的保性能控制問題研究[J].山東大學(xué)學(xué)報(bào):理學(xué)版,2009,44 (5):56-61. [9] 俞立.魯棒控制—線性矩陣不等式處理方法[M].北京:清華大學(xué)出版社,2002. [10] 裴冀南.具有時(shí)滯的線性系統(tǒng)的漸近穩(wěn)定[J].四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2001,24(2):151-153. [11] 方建印,王利萍,叢梅艷.一類不確定非線性離散時(shí)滯性系統(tǒng)的魯棒鎮(zhèn)定問題[J].鄭州大學(xué)學(xué)報(bào):理學(xué)版,2006,38(3): 10-16. [12] 卜春霞,鄭寶杰,趙安娜.一類不確定時(shí)滯系統(tǒng)的H∞問題[J].鄭州大學(xué)學(xué)報(bào):理學(xué)版,2005,37(2):33-37. [13] 虞繼敏,季潔坤,莫玉忠.一類線性擾動(dòng)中立型不確定系統(tǒng)的H∞問題[J].鄭州大學(xué)學(xué)報(bào):理學(xué)版,2005,37(3):23-27. Guaranteed Cost Control Problems for a Class of Impulsive Switched System with Time Delay and Uncertain Parameters MAO Bei-xing1, MU Xiao-w u2, BU Chun-xia2 Guaranteed cost control p roblem sare investigated for a discrete impulsive sw itched system w ith norm-bounded uncertain parametersand invariant time delays.Based on Lyapunov theory and linear matrix inequality(LM I)techniques,a sufficient condition fo r the existence of guaranteed cost state feedback controller of impulsive sw itched system is derived.So it is convenient to be realized. impulsive sw itched system;guaranteed cost control;time delay O 231.1 A 1671-6841(2010)03-0007-04 2009-09-07 航空科學(xué)基金資助項(xiàng)目,編號(hào)2008ZE55004;鄭州航空工業(yè)管理學(xué)院青年基金資助項(xiàng)目,編號(hào)Q08SL003. 毛北行(1976-),男,副教授,碩士,主要從事非線性系統(tǒng)研究,E-mail:maobeixing329@zzia.edu.cn.

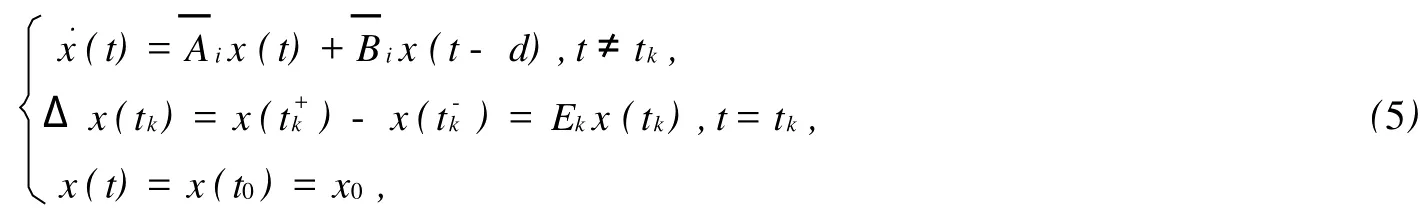
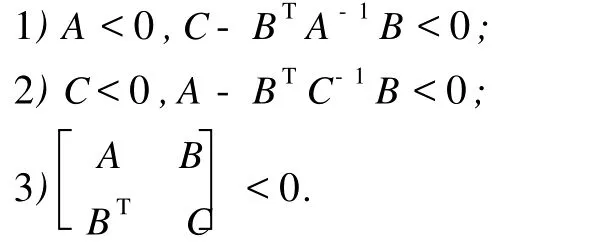
2 主要結(jié)果

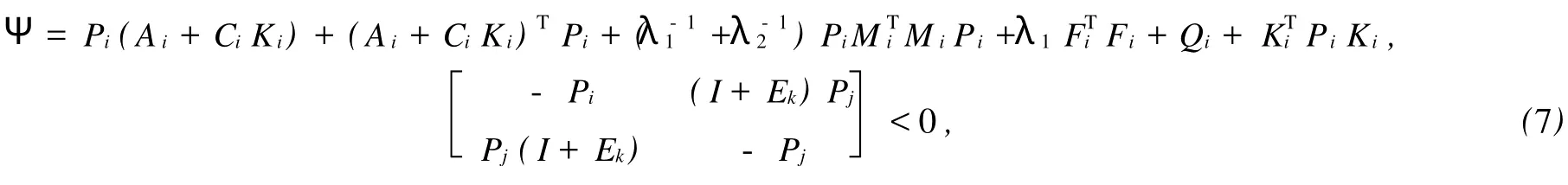

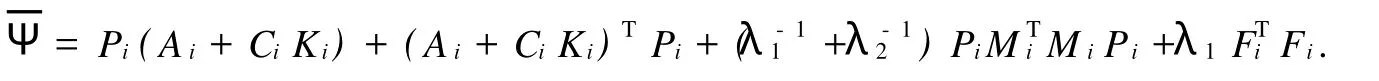
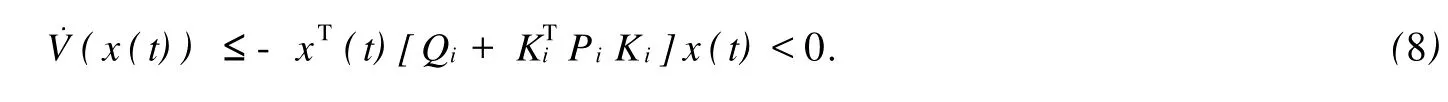
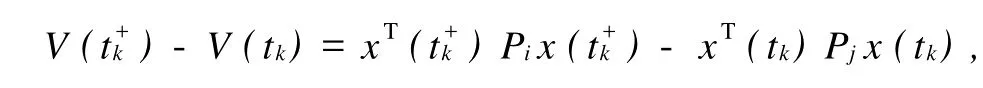
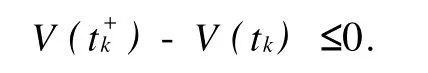
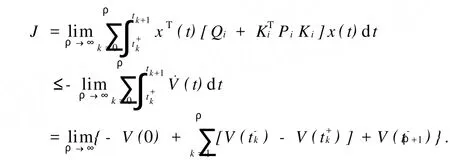
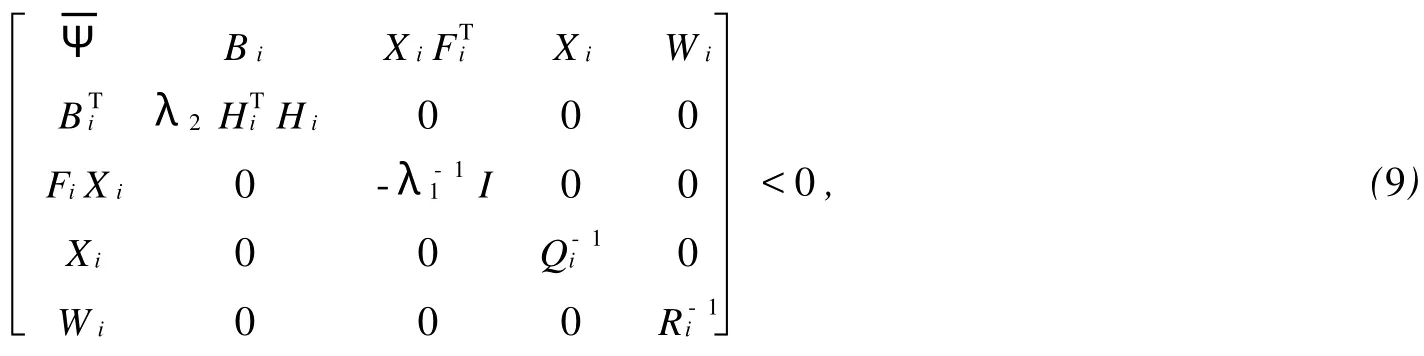
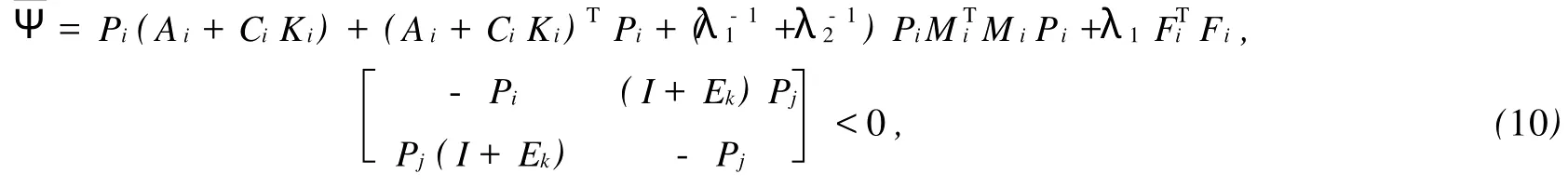
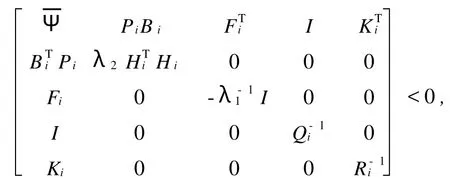
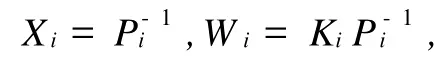
3 結(jié)束語
(1.Department of M ath and Physics,Zhengzhou Institute of Aeronautical Industry M anagement, Zhengzhou 450015,China; 2.Department of M athematics,Zhengzhou University,Zhengzhou 450001,China)

