Efficient single-pixel imaging encrypted transmission based on 3D Arnold transformation
Zhen-Yu Liang(梁振宇), Chao-Jin Wang(王朝瑾), Yang-Yang Wang(王陽陽), Hao-Qi Gao(高皓琪),Dong-Tao Zhu(朱東濤), Hao-Li Xu(許顥礫), and Xing Yang(楊星),?
1State Key Laboratory of Pulsed Power Laser Technology,National University of Defense Technology,Hefei 230001,China
2Advanced Laser Technology Laboratory of Anhui Province,Hefei 230001,China
Keywords: single-pixel imaging,3D Arnold transformation,elliptic curve encryption,image encryption
1.Introduction
Single-pixel imaging (SPI)[1]has gained much attention in recent years due to its potential in recovering 2D or 3D scene information from 1D light signals using single-pixel detectors.This is particularly relevant to the fast-growing modern spatial light modulation techniques.SPI systems have the potential for a wide range of applications in remote sensing,[2-4]laser radar[5-10]and low-dose x-ray medical imaging[11,12]due to the flexible optical field control,high sensitivity and resistance to atmospheric turbulence.
Compared with traditional imaging techniques,SPI lowers the requirements on detectors.As compensation, this technique requires more measurements and is thus timeconsuming.Numerous methods have been put forth to increase the image formation speed and image quality of SPI.By employing image priors such as sparsity,compressive sensing algorithms[13,14]can drastically reduce the measurements required to produce a high-quality image under random illuminations.Instead of random patterns, deterministic modelbased SPI approaches use orthogonal basis patterns,for example the Fourier[15]and Hadamard[16]approaches,for SPI modulation to eliminate redundancy between different illuminations.Additionally,deep learning has been used for SPI[18-21]reconstruction algorithms.The trained deep neural network can be used to improve imaging quality while retaining high computational efficiency.
Apart from SPI modulation and reconstruction methods research,the principle of SPI,which transforms 2D or 3D image data into a 1D light signal,also offers promising prospects in image compression and transmission.However,during data communication,these unusual light signals in public channels can easily attract the attention of eavesdroppers.Traditional techniques for encrypting optical images, such as random phase mask (RPM),[22,23]optical inference principle-based encryption,[24,25]phase retrieval algorithms[25]and computer holography,[26,27]are usually capable of providing high-speed parallel processing and secure transmission of 2D images by hiding information of varied dimensions.In recent years,Laiet al.[28-31]have proposed a series of well-designed chaotic systems to realize high-security image encryption.By controlling the dimensions of chaotic signals, encryption operations can be performed in high-dimensional spaces.
Unlike the traditional encryption methods, the issues of SPI-based optical encryption are now receiving everincreasing attention as they provide an alternative for solving problems in optical information processing.Previous works[32-36]have focused on modulating the target scenes through a series of computer-generated pseudo-random patterns.These patterns are treated as secret keys shared only between the sender of the message and its authorized recipient.The light intensity signals of the single-pixel detector are then encrypted and transmitted as ciphertext to ensure secure communication.Scrambling orthogonal basis patterns is a type of encryption transmission scheme that differs from direct encryption transmission using pseudo-random patterns.[37-41]The message sender utilizes a set of rules to modulate the target light field, typically using only the sampling strategy and scrambling rules of orthogonal basis patterns as the secret key.These methods not only improve the quality of decrypted images but also reduce the key space.In addition to orthogonal basis pattern encryption, there are other types of single-pixel encryption schemes, such as visual cryptography,[42]watermarking and steganography techniques[43-46]and encryption with a metasurface key.[47]
Despite the advantages of single-pixel encryption schemes,existing methods still face several major issues such as severe noise in the decrypted results, difficulty in ensuring key transmission security and complex rules for designing orthogonal basis patterns.To address these issues, we propose an SPI encrypted transmission scheme based on 3D Arnold transformation and elliptic curve cryptography.The proposed method does not require complex pixel permutation rules for orthogonal basis patterns.Instead, it employs Hadamard patterns to illuminate the scene, and then uses the 3D Arnold transformation to permutate the 1D light signals of the single-pixel detector(plaintext information).The transformation parameters serve as the secret key, while the security of key transmission is guaranteed by an elliptic curve-based key exchange mechanism.Compared with existing encryption schemes, our proposed technique not only enhances the security of encryption but also eliminates the need for complicated pattern scrambling rules and solves the problem of secure key transmission.As a result, both the security and quality of information decryption are ensured.In summary,our main contributions can be summarized into three points:
(1) We propose a random scramble method that directly transforms the 1D single-pixel light signals and eliminates the need for the design of a complex illumination pattern.Our proposed method not only greatly enhances the security of transmission of single-pixel detection data but also maximizes the accuracy of decryption results.
(2)We present a 3D Arnold transformation-based 1D signal scrambling method that has achieved satisfactory encryption results on various images while demonstrating state-ofthe-art performance across different sampling rates.
(3) We develop an elliptic curve-based key exchange mechanism with the proposed 1D signal scrambling method.This mechanism further enhances the security of key transmission by overcoming the challenges associated with conventional symmetric single-pixel encryption schemes.
2.Methodology
In this section,we first utilize non-scrambling Hadamard patterns to illuminate the scene.Then,we propose a novel 3D Arnold scramble method for a 1D single-pixel detection signal on the basis of a differential detection system.Finally,we introduce an elliptic curve-based key exchange mechanism to encrypt the Arnold transformation parameters.At the end of this section,we briefly explain how to encrypt and decrypt using the 3D Arnold method and the key exchange mechanism using a practical example.The schematic of whole technique is shown in Fig.1.

Fig.1.Schematic of our proposed technique: (a) signal plaintext generation process, (b) encryption process, (c) decryption process (ECC,elliptic curve cryptography).
2.1.Structural illumination with Hadamard patterns
In a typical SPI framework, a 1D light intensity signalb(i)is obtained by actively illuminating the sceneT(x,y)with pre-designed two-dimensional patternsI(i)r(x,y).The singlepixel detector records the reflected or transmitted signals by the scene
The illumination patterns can be designed in various forms, such as random intensity patterns or orthogonal basis patterns.In our method, we utilize Hadamard basis patterns to illuminate the scene,and the single-pixel detection 1D light signal is mathematically equivalent to the inner product between the Hadamard basis patterns and the scene

Based on differential detection, 1D light signals can be separated into two components,bH+andbH-, which are utilized in the subsequent encryption process.
2.2.The 3D Arnold transformation for single-pixel 1D detection signal
The Arnold transformation,also known as the Arnold cat map,[48]is a method of discrete chaotic mapping that repeatedly folds and stretches input images within a limited region.Due to its well-established chaotic characteristics and easily controllable parameters,it is widely used in digital image encryption.The commonly used Arnold transformation is the 2D form
wherexandydenote the original position of any pixel in the image,x′andy′indicate the transformed pixel location,aandbserve as controlling factors andNis the dimension of the square image.
To achieve more secure and efficient pixel transformations,the 2D Arnold transformation can be extended to higher dimensions.By introducing new parameterscandd, the higher-dimensional 3D Arnold transformation[49]has been developed
wherezrepresents the grayscale value at any pixel location(x,y), andz′denotes the transformed grayscale value.To facilitate computation,we have employed the modified form of the 3D Arnold transformation proposed by Liuet al.[50]
wherepandp′denote the grayscale values at the same pixel location before and after transformation,respectively.Mrepresents the maximum grayscale value of the image, which is usually 255 (for an 8-bit grayscale image from 0 to 255).It implies that not only the pixel positions of the image are disordered,but also the grayscale values of the image are scrambled.This will further enhance the security of image encryption.The plaintext image can be recovered by applying the inverse 3D Arnold transformation to the ciphertext resulting from the following equation:
Therefore, utilizing the 3D Arnold transformation for image encryption would result in a more robust security effect compared with the 2D transformation method.It is difficult for an attacker to obtain accurate results if the encryption key or algorithm remains confidential.
In this paper, we propose the idea of applying the 3D Arnold transformation to 1D light intensity signals.As shown in Fig.1, we transform the single-pixel detection values acquired into 2D matricesH+andH-of light intensity.It should be noted that while pixel values in image encryption applications can be quantified using a grayscale value of 255,the single-pixel measurement values typically differ from image grayscale values.Therefore,in practical implementation,we utilize the maximum value in the light intensity as one of the transmitted parameters for the 3D Arnold transformation of the light intensity matrix.
2.3.Elliptic curve Diffie–Hellman key exchange
Elliptic curve cryptography(ECC)is a public key encryption method proposed by Koblitz and Miller in 1985.[51]It is based on the theory of elliptic curves.By utilizing the discrete logarithm difficulty of the Abel group composed of points on an elliptic curve over a finite field, it can achieve encryption,decryption and a digital signature.By associating addition operations in elliptic curves with modulo multiplication operation in a discrete logarithm,it is possible to establish a corresponding cryptographic system based on elliptic curves.Compared with the traditional public key encryption system RSA,ECC requires a significantly smaller of key size to achieve the same level of security performance.Here, an elliptic curve that satisfies the Weierstrass equation over a finite field Fpis defined as
wherex,y,α,β ∈Fp,and satisfies 4α3+27β2?=0.The security of the elliptic curve encryption mechanism is based on the difficulty of solving the discrete logarithm problem on elliptic curves.Assuming two pointsGandQon an elliptic curve,whereQ=KGfor some integerK.Although it is relatively easy to calculateQusing the four arithmetic operations of finite field,computingKfromGandQis a highly challenging task.Here,Gis referred to as the base point,Kis the private key andQis the public key.
The elliptic curve Diffie-Hellman(ECDH)key exchange mechanism combines elliptic curves with the Diffie-Hellman protocol[52]to provide a shared key exchange method over an insecure channel.The process involves the following steps:
(1) The server publicly selects an elliptic curve and randomly chooses a point on the curve,which is referred to as the base pointG.Simultaneously, a random positive integerKis selected as the private key,while the corresponding public keyPsis generated and made available to the public.
(2) The user selects an arbitrary positive integerNuas their private key based on the elliptic curve and base point selected by the server.Subsequently,a corresponding public keyPu=NuGis generated and made publicly available to the user.
(3) The server and user compute a shared ECDH key based on their respective private keys.
For the server
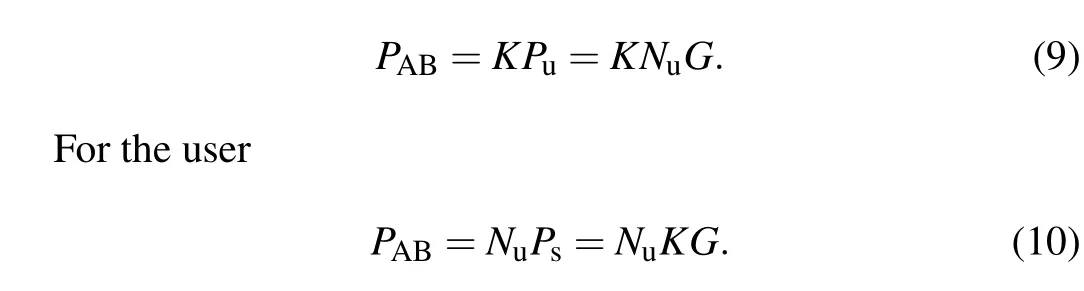
In this paper,we adopt the idea of applying the ECDH key exchange mechanism to the chosen parameters from 3D Arnold transformation.As shown in Fig.1,we first embed the secret key in the 3D Arnold transformation,such asa,b,Mand the iteration times, into an elliptic curve.Subsequently, a private key is randomly selected to generate an exchangeable public key.The key is then further encrypted using the four arithmetic operations of finite field.Finally, the secure transmission of the key in the public channel is realized.
2.4.Encryption and decryption process
The proposed encryption process mainly consists of six steps:
Step 1 Record the light intensity values of an SPI system based on Hadamard differential detection;these are subsequently transformed from the one-dimensional vector format to the two-dimensional differential light intensity matrixH+andH-.
Step 2 Apply 3D Arnold transformation toH+andH-.The transformation parameters such asa,b,c,d,N,Mand the iteration times serve as secret keys.
Step 3 Randomly choose an elliptic curveEp(α,β); a random point on the curve serves as the base pointG.Then the server selects a random positive integerKto generate the public keyPs=KG.All of above information is shared with the user through a public channel.
Step 4 The server embeds the parameters into the selected curve.Consider parameterMas an illustrative example.Pmdenotes a point on the embedded elliptic curve.
Step 5 After receiving the elliptic curve from the server,the user selects a random positive integerNuas a private key,and generates a public keyPu=NuGwhich can be shared in public channel.
Step 6 The server receives the public keyPufrom the user, and generates ciphertext byC=Pm+KPu.The ciphertext and encrypted single-pixel detection values can be shared with the user in a public channel,thus completing the encryption process.
The proposed decryption process mainly consists of three steps:
Step 1 After receiving the ciphertext and encrypted single-pixel detection values from the server,the user decryptsPmby using the private keyNu
Step 2 Extract the 3D Arnold transform parameters fromPmby embedding rules,and apply an inverse 3D Arnold transform to recover the single-pixel detection plaintext.
Step 3 Apply an inverse Hadamard transform algorithm or other compressed sensing algorithms; the original image information can be reconstructed,thus completing the decryption process.
3.Results
In this section the proposed method is verified by both computer simulation and optical experiments.
3.1.Simulation results
To validate our method, we perform computer simulations on Intel CPU i7-12700KF@3.60 GHz hardware with 32 GB RAM.The gray-scale image ‘Cameraman’ is used as the ground truth.
3.1.1.Encryption and decryption process
Firstly, we generate 64×64 Hadamard patterns with a ‘zigzag’ order.[53]The 1D single-pixel detection signal is shown in Fig.2(b).It is obvious that the unencrypted singlepixel intensity values are concentrated and exhibit a conspicuous regularity.If an eavesdropper has a certain knowledge of Hadamard transformation,they can easily identify that this signal has been encrypted using an SPI system.The eavesdropper can directly use the inverse Hadamard transformation to obtain the correct image information, which would expose a significant risk of data leakage.
Secondly, we set the controllable parameters in a 3D Arnold transformation,a=b=3,c=d=7,M=1994,and the iteration times are set as 10.The plaintext of single-pixel light intensity values is directly encrypted into ciphertext via selected parameters.The generated ciphertext signal is depicted in Fig.2(c).It can be observed that the single-pixel light intensity values applying the proposed scrambling method resemble noise, lacking any discernible rules or orders.If an eavesdropper does not have access to the decryption key, using the inverse Hadamard transformation algorithm alone will not be sufficient to obtain accurate target image information,as illustrated in Fig.2(d).
Finally, we achieve encryption using the parameters set in the 3D Arnold transformation through the ECDH key exchange mechanism,as detailed below:
(1) We select an elliptic curve withp= 123457,α= 5376,β= 2438 and randomly choose a pointG=(2225,75856)on the curve.
(2) Considering parameterMas an illustrative example,we utilize the value ofMas the horizontal axis on the curve,of which the embedding pointPmis(1994,104163).We set the server’s private keyK=35,and the public keyPsis(112799,97369).
(3)The user receives elliptic curve parameters andPsin a public channel,and shares the public keyPu=(94953,15581)by setting the private keyNu=95.
(4)We generate ciphertextC=(106784,55261),and the encryption process is completed.
(5)The user decrypts the ciphertext according to Eq.(11),which will recover the controllable parameters of the 3D Arnold transformation.Then, the user applies the inverse 3D Arnold transformation to reconstruct the original single-pixel light signals,and the decryption process is completed.

Fig.2.Simulation results: (a)the ground truth‘Cameraman’;(b)single-pixel detection light signal without encryption;(c)signal encrypted by 3D Arnold transformation;(d)recovered image without the correct key;(e)recovered image with the correct key.
3.1.2.Security analysis
To further illustrate the security of our proposed method,in this section we discuss the security analysis of the proposed method, for example correlation analysis, sensitivity analysis with respect to the key and plaintext.
(1) Correlation analysis We have calculated the correlation coefficient (CC) between plaintext and ciphertext for quantitative evaluation.CCis defined as follows:
whereAandBdenote two different two-dimensional distributions andmandnare the indices of the rows and columns,respectively.In this paper,Arepresents the encrypted image after 3D Arnold transformation andBrepresents the original image.The security of encryption is determined by calculating theCCvalue betweenAandB.The higherCCis,the stronger the correlation between the two images, indicating a lower level of security.Furthermore, if theCCvalue is negative,it indicates that the two images are negatively correlated.We conduct a comparative analysis between the proposed methodology and two baseline SPI encryption techniques: Hadamard patterns permutation (HPP) and random patterns (RP).The grayscale images‘Cameraman’and‘Baboon’are also adopted as two typical ground truths.In addition,theCCvalues under different sampling ratios are also calculated.Table 1 shows theCCvalues for the simulation, whereMbdenotes the permutation block size in HPP.
According to the results presented in Table 1,it can be observed that theCCvalues for the reconstructed images without the correct key are significantly lower than for the other two baseline methods.The results indicate that when applied to the same object, our proposed method yields the smallestCCvalue at sampling ratios of 0.1, 0.25 and 1.When the sampling ratio is 0.5, although theCCvalue obtained by our method is not the minimum it is similar to the comparable values.Meanwhile,for the same object,when the sampling ratio changes, theCCvalues obtained by our proposed method do not change significantly.In other words,our proposed method has the lowest sensitivity to the sampling ratio itself.
(2) Sensitivity analysis An ideal encryption procedure should be sensitive with respect to the secret key, i.e., the change of a single bit in the secret key should produce a completely different encrypted image.We measured the number of pixel changing rate(NPCR)and unified averaged changed intensity(UACI)values to see the influence of changing a single pixel in the original image on the encrypted image using the the proposed method.We take two encrypted imagesCandC′,whose corresponding original images have a difference of only one pixel.NPCR and UACI are defined as

The results of NPCR and UACI are shown in Table 2.According to the results, NPCR and UACI values for the reconstructed images using our method are significantly better than for the other two methods.These results indicate that this method can provide higher security than existing methods.
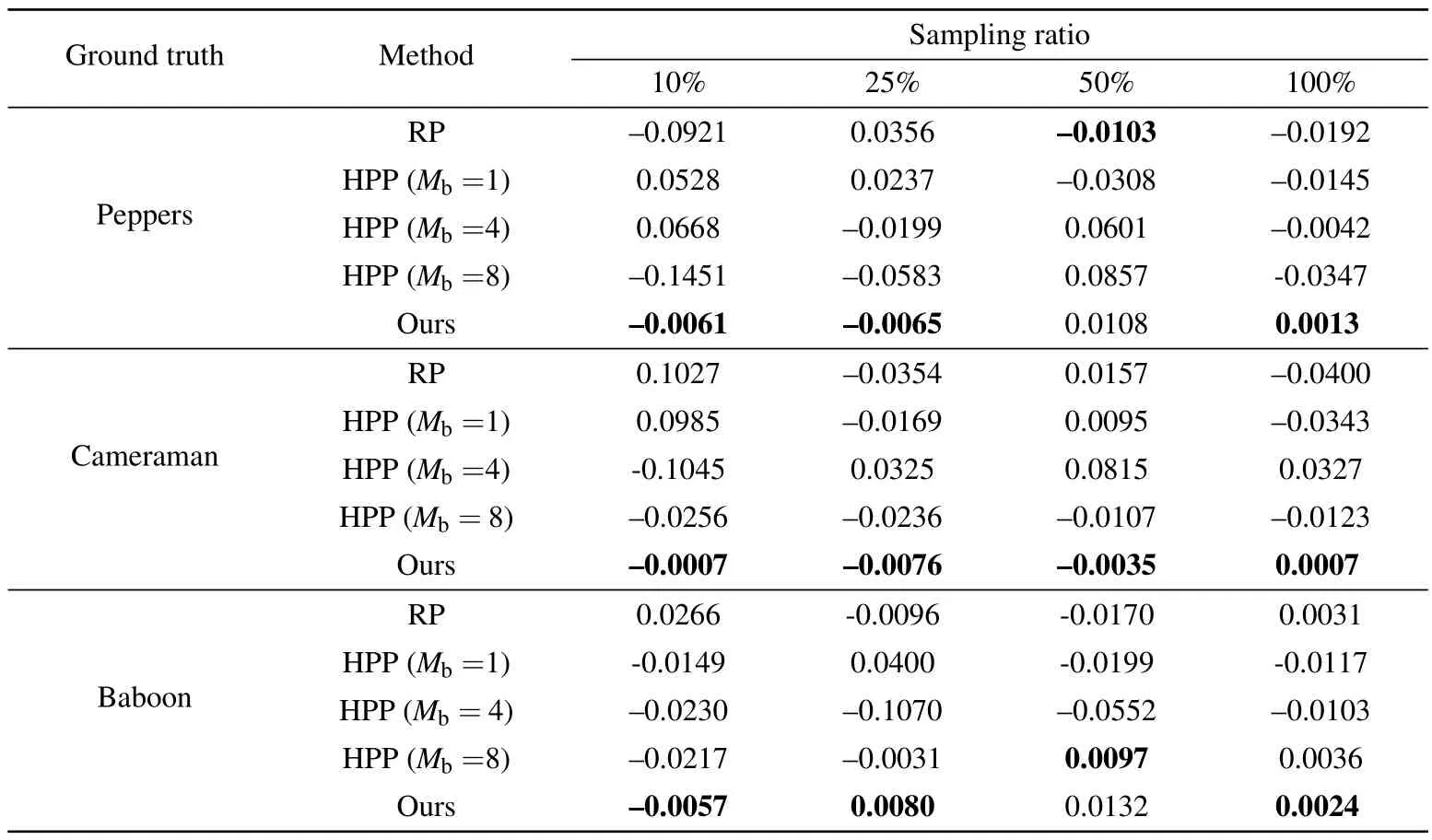
Table 1.Results for CC values.

Table 2.Results for NPCR and UACI values.
3.1.3.Analysis of decrypted image quality
We also conduct a comparative evaluation of the quality of image reconstruction with the correct key.The reconstructed results under different sampling ratios are shown in Fig.3.

Fig.3.Simulation results of the decryption process with the correct key at different sampling ratios.(a1)-(a6)Reconstruction images using the RP method.(b)-(d)Reconstruction images using the HPP method with different pixel permutation parameters Mb.(e1)-(e6)Reconstruction images using our proposed method.
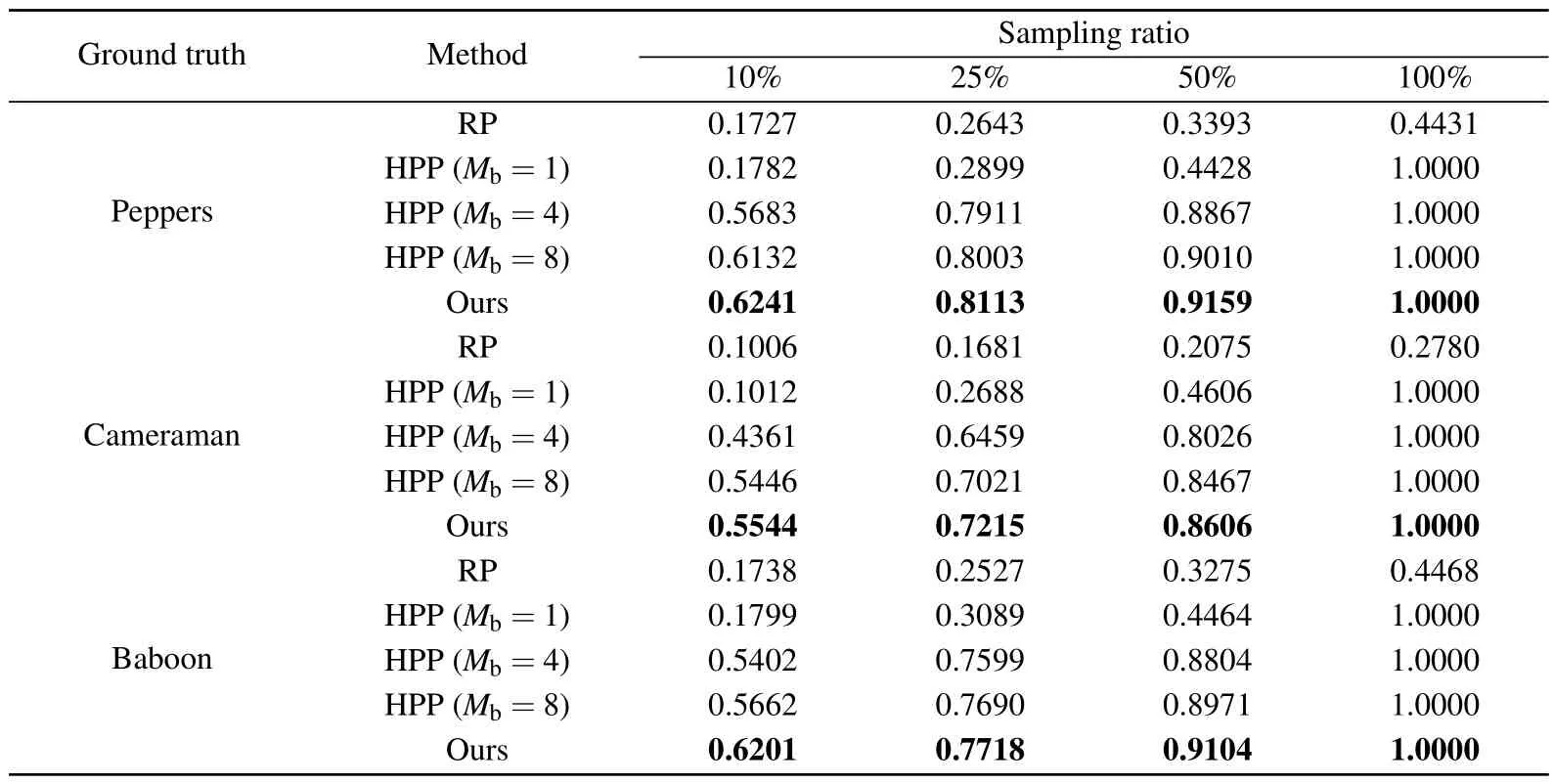
Table 3.The SSIM results of image reconstruction.
As shown in Fig.3, the quality of reconstructed image with the correct key improves as the sampling ratio increases in the three schemes.It is evident that the RP and HPP(Mb=1, 4) methods are more susceptible to the influence of the sampling ratio.Our proposed method exhibits a degree of visual similarity that is comparable to that of the HPP(Mb=8)method, which demonstrates that the proposed technique can achieve a better quality reconstructed image than other two baseline methods.To quantitatively evaluate the quality of reconstruction images,the structural similarity index(SSIM)[54]is employed.
The SSIM results are shown in Table 3.For the same sampling ratio, our proposed method achieves the best SSIM value for different ground truths.Therefore,the above results suggest that our proposed method not only achieves more secure encryption,but also produces a competitive reconstructed image.
3.2.Experimental results
We performed an experiment to demonstrate the proposed technique.A printed character ‘3’ was used as an object.A schematic of our experimental setup is shown in Fig.4.We used a DLP development kit (DLP 4710EVM-LC) for spatial light illumination, and generated Hadamard patterns in a zigzag order.A Si switchable gain detector (Thorlabs PDA100A2)was used to measure the intensity of the reflected light from the object.The electronic signals were transferred to the computer via a data acquisition board(NI USB-6343).

Fig.4.Diagram of the experimental setup:DLP,digital light processing development kit (DLP 4710EVM-LC); detector, single-pixel detector(Thorlabs PDA100A2);DAQ,data acquisition board(NI USB-6343).

Fig.5.Experimental results of encryption and decryption at different sampling ratios.(a)-(c) Reconstruction images using our method.(b)-(j) Reconstruction images using the HPP method with different pixel permutation parameters Mb.(k),(l)Reconstruction images using the RP method.
Figure 5 shows the experimental results of the reconstruction for different sampling ratios.The first(top)panel displays the recovered encrypted image and final decrypted image produced by our proposed method with different sampling ratios.The second panel showcases the original image without encryption for various sampling ratios.The third panel illustrates the recovered encrypted image and final decrypted image produced by HPP with differentMbvalues and sampling ratios.At the bottom of this panel, reconstructions by original Hadamard SPI without encryption are shown for different sampling ratios.Finally, the fourth panel displays the recovered encrypted image and final decrypted image produced by conventional encrypted ghost imaging with random illumination patterns for different sampling ratios.
The quality of the reconstructed image improves as the sampling ratio increases in three schemes.It is evident that the RP and HPP(Mb=1,4)methods are more susceptible to the influence of sampling ratio.Our proposed method exhibits a degree of visual similarity that is comparable to that of the HPP(Mb=8)method.It can be observed that the object scene is not recognizable from the reconstruction algorithm for different sampling ratios.In the second panel,the quality of the decrypted images is unaffected by encryption operation compared with the reconstructed images in the third panel.The experimental results are consistent with the simulation results.
4.Conclusion
In summary, we propose an efficient framework for encrypted transmission of SPI data.We employ direct scrambling of the 1D light signal from the single-pixel detector instead of generating pseudo-random illumination patterns or designing complex permutation rules for orthogonal basis patterns.The improved 3D Arnold transformation in 1D signal encryption operations introduces stronger security for the encryption system.To solve the problem of key transmission in public channels, we construct a secure key transmission mechanism by applying the ECDH key exchange protocol.Simulation and experimental results demonstrate our proposed scheme,ensuring both security and good quality decryption of information.This work generates new insights for encrypted transmission of SPI data and provides a solution for developing a secure SPI data communication system for remote sensing or laser radar.
Acknowledgements
The authors thank Mr Yi Chen and Mr Xie Bo for their precious time and invaluable comments on this work.
Project supported by the National Natural Science Foundation of China(Grant No.62075241).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

