Yuqing Zhang(張宇青) and Youming Lei(雷佑銘),2,?

1School of Mathematics and Statistics,Northwestern Polytechnical University,Xi’an 710072,China

2Ministry of Industry and Information Technology Key Laboratory of Dynamics and Control of Complex Systems,Northwestern Polytechnical University,Xi’an 710072,China

Keywords: logical stochastic resonance,bifurcation,mean first passage time

1.Introduction

In practice, many physical systems are connected to noise.Intuitively it was thought that noise always plays a destructive role.However, with the development of stochastic dynamics it has been discovered that noise can produce unexpectedly ordered behavior in nonlinear dynamical systems.An example of such a phenomenon is stochastic resonance(SR),initially suggested by Benziet al.[1]and Nicolis.[2]Under certain conditions (the combination of external periodic forces,noise and the nonlinearity of the system),an appropriate noise input maximizes the response of the nonlinear system to a weakly periodic signal, giving rise to a ‘resonance’phenomenon.SR has been applied to many fields, including weak signal detection,[3]image processing,[4]biological systems,[5,6]energy harvesting,[7,8]neural networks,[9-11]mechanical fault diagnosis,[12,13]etc.

Logical stochastic resonance (LSR) provides a completely new method for building reliable logic gates, which was initially suggested by Muraliet al.[14]Research has revealed that when two square waves act as input signals, a bistable system can generate a logic output under optimal noise.Moreover, as the noise increases, the success probability of the system response first rises and then falls.Then the LSR phenomenon was confirmed in an electronic circuit model.[15]Inspired by this pioneering study, numerous earlier publications concentrated on the separate study of LSR in bistable or tristable systems.For instance, Gaussian colored noise[16]and non-Gaussian noise,[17]such as sine-Wiener noise,[18]L′evy noise.[19]andα-stable noise,[20]have been shown to produce logic operations in bistable systems.In addition, it has been demonstrated that correlated internal and external noises[21-23]can also produce logic operations in bistable systems.It has also been shown that other elements can produce logic operations in bistable systems,including system parameters,[24]time delay,[25-27]coupling between two subsystems,[28]and periodic and non-periodic forces.[29-31]Since three different inputs correspond to two outputs in a bistable system this may cause information to be lost, making XOR logic unattainable.Storniet al.[32]expanded upon the existing research in bistable systems and applied it to a tristable system,consequently resulting in the attainment of XOR logic.Subsequently Zhanget al.[33,34]researched the LSR phenomenon of a tristable system driven by Gaussian colored noise and non-Gaussian noise, and confirmed the LSR phenomenon in analog circuits; however, for bistable and multistable systems which is better suited to produce reliable logic operations? Luet al.[35]investigated the LSR performance of a tristable system and traditional bistable system.Liaoet al.[36]compared the LSR performance of a proposed quadstable system and tristable system as reconfigurable logic gates.Previous studies had considered two different systems: for the same system with bistable and tristable regions, which is more suitable for generating logic operations? Therefore, we can consider a cross-bifurcation nonsmooth system with a bifurcation parameter resulting in an alteration in monostability,bistability and tristability.

Since it is common for a nonlinear system to bifurcate from a bistable state to a multistable one due to friction and collision,study of stochastic resonance in a bifurcation system is unavoidable.Kanget al.[37]studied a single-mode nonlinear optical system and demonstrated that the dependence of the relaxation rate on the noise intensity in monostable and multistable cases exhibited a large difference.It is well known that the changing of parameters in nonlinear systems can cause bifurcation cascades, in which existing branches of states are eliminated and new states emerge.Nicolis and Nicolis[38]considered a nonlinear stochastic dynamical system with a bifurcation parameter across monostable, bistable and multistable regimes.They came up with analytical equations for the response and optimal responding conditions for the bifurcation parameter, the noise amplitude and the frequency of external excitation based on response theory.Lei and colleagues[39,40]studied a non-smooth system with a controllable parameter that bifurcates as the controllable parameter changes.They discussed the SR phenomenon in bistable and multistable areas.It was demonstrated that the multistability of the system improves the optimal transition rate and the optimal response amplitude of the system.

In this work,we consider a cross-bifurcation non-smooth system with a bifurcation parameter that transits from tristable to bistable regions as the bifurcation parameter changes.Therefore,we focus on the effect of the bifurcation parameter on the LSR in different regions.In Section 2,we describe the cross-bifurcation non-smooth system under Gaussian colored noise excitation.In Section 3,we conduct a bifurcation analysis for this system and derive expressions for the generalized potential function and the mean first passage time(MFPT)in the bistable and tristable regions, respectively.The success probability is introduced to measure the reliability of logic response,and the difference in LSR in bistable and tristable areas is discussed.The conclusions are drawn in Section 4.

2.Cross-bifurcation non-smooth system and measurementof LSR

In this section we consider a cross-bifurcation nonsmooth system under Gaussian colored noise excitation.The Langevin equation of the system has the following form:

whereDis the noise strength andτis the correlation time.

UsingNinputs to generateNsquare waves,a logical correspondence between inputs and outputs can be established.Specifically,Iis a low-amplitude input,I=I1+I2, whereI1andI2encode the two logic inputs.We drive the crossbifurcation non-smooth system with the signalI.The logic inputs can be 0 or 1,so there are four different logic input sets(I1,I2): (0,0), (1,0), (0,1) and (1,1).The signalI1,2has a value of-Kfor a logical 0, whereas it takes on a value ofKfor a logical 1.Since the input sets (0,1) and (1,0) produce the sameI,the four different input conditions(I1,I2)produce three differentIvalues:-2K, 0, 2K.As a result, the input signalIis a three-level aperiodic waveform.

3.Logical stochastic resonance under colored noise

The potential function corresponding to Eq.(1)takes the form

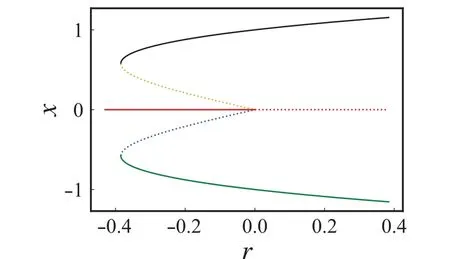
Fig.1.Bifurcation diagram of system(1)on the bifurcation parameter r.At r=-2/9,the system has two saddle-node bifurcations making the system change from monostable to tristable.At r=0, the system has a subcritical pitchfork bifurcation making the system change from tristable to bistable.

3.1.Bistability

In the bistable region,the system has two symmetrical potential wells, but there are three different logical inputs.This results in a memorable output value when the logical input is 0.In other words,the output value is determined by the output value of the previous state.Specifically,if the previous output is-1,then the current output will also be-1,and if the previous output is 1,then the current output will be 1.Therefore,with reference to Table 1 we find that the logic response of the system cannot realize a reliable logic operation,for which a bias parameter is added to deflect the potential.Thus, the Langevin equation is rewritten as

wheref(x)=x-x3+rsgn(x)+GandGis a bias parameter.

As shown in Fig.2,the tilt of the potential function is determined by the bias parameterG.WhenG ＞0, the bistable potential function tilts to the right,as shown by the red dashed line in the figure.When the logic input is 0, the particle will be in the well atx+.With reference to Table 1 we find that in this case the system can implement an OR/NOR logic operation.WhenG ＜0, the bistable potential function tilts to the left,as shown by the green dotted line in the figure.When the logic input is 0,the particle will be in the well atx-.With reference to Table 1 this reveals that the system can implement AND/NAND logic operations.

Fig.2.Potential well for various G values.The blue line denotes the symmetric bistable well, the green line denotes the AND/NAND logic operation and the red line denotes the OR/NOR logic operation.

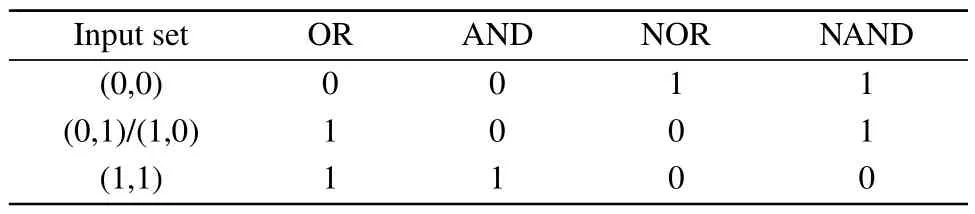
Table 1.For the four logic operations,the connection between the four input sets and the outputs.

The logical output of the system is decided by its state.For example,if its state is in one well,the output can be considered as a logical 1,and if it is in another well,the output can be considered as a logical 0.Specifically for a bistable system with two potential wells atx+andx-,the logical output of the system is considered to be 1 when its state is in right well(x+)and it is considered to be 0 when its state is in left well(x-).The output is thus‘toggled’when the system switches wells.According to Table 1 the system can implement the required types of logic gates.

The potential function corresponding to Eq.(6)takes the form

In the bistable region, pointx3is unstable when the system is non-smooth so the Gaussian approximation cannot be used.Thus, the steepest-descent approximation allows us to estimate the following:

whereNis a normalization constant and the generalized potential functionUghas the following form:

Consider the logic input parameterKto take the value 0.4.Figure 3 displays the response of the system in Eq.(6)at different noise intensitiesDwhen the bifurcation parameterr=0.2 and the bias parameterG=0.3.The red line indicates the logical input and the blue line indicates the output of the system.It can be found that for very weak noise(D=0.01)at some moments the state of the particle depends on the previous state at times,for example[8000,8500],[10000,12000].The particle cannot produce a transition and does not move to the desired potential well.For optimal noise (D=0.2), the particle is located in the left well when the input is-0.8,and the particle is located in the right well when the input is 0 or 0.8.According to Table 1,if statex ＜0 is interpreted as logical output 0 and statex ＞0 as logical output 1, the system produces a stable OR logic behavior,whereas if statex ＞0 is interpreted as logical output 0 and statex ＜0 as logical output 1, the system produces a stable NOR logic behavior.In the same way,by setting the bias parameter atG=-0.3,we can achieve clean AND/NAND gates at an optimal noise intensity.With the enhancement of noise(D=0.5),due to frequent transitions of particles, the system gradually produces the wrong logic outputs.Thus, noise-induced logic operation becomes unreliable and the LSR phenomenon is destroyed.

In order to measure the reliability of noise-induced logic operation, we introduce the concept of success probability.The success probabilityPis expressed as

Fig.3.The logic output x(t)with r=0.2 corresponding to(a)D=0.01,(b)D=0.2, (c)D=0.5.The dashed red line indicates the logical input I, consisting of a combination of I1 and I2 which take the value-0.4 when the logic input is 0 and 0.4 when the logic input is 1.Clearly,when D=0.2,we get the desired OR gate.

whereNis the overall number of runs andSis the number of correct logic outputs.WhenPapproximates to 1, the system generates a reliable logic operation.Using computer simulations to generate sets of logic inputs and continuously inputting different combinations of logic inputs to the system,the success probability can be obtained.The logic input has four possible input sets(I1,I2):(0,0),(0,1),(1,0)and(1,1).Each run is a random permutation of all the above sets,where each signal input set drives the system for a period of time with time step Δt= 0.01 s and 1000 s.Then the obtained output is compared with the desired logic output to obtain the correct probability of this set.When this correct probability is above a certain threshold,the set of logic outputs is considered correct.A run is deemed successful only when all four logic outputs are correct.can be seen that the system appears to have an optimal window of noise, and the optimal window is related tor.Whenr ＞0, the optimal window of noise decreases asrincreases and moves to a greater noise strength.Figure 5 depicts the image of the generalized potential function for different values ofr, from which it can be found that the height of the potential barrier is affected byr.Whenr ＞0,there is a subsequent increase in the potential barrier asrincreases.Therefore asrincreases, a higher noise intensity is required to enable particle transition.WhenI=0 the particle can transit to the right well with appropriate noise excitation, as shown in Fig.5(a),and whenI=-0.8 the particle can transit to the left well with appropriate noise excitation as depicted in Fig.5(b).Thus,the optimal window of noise moves to a greater noise strength asrincreases.Figure 6 shows that in the bistable region the transition rate decreases asrincreases.Thus asrincreases,a larger noise intensity is required to make the system produce the LSR phenomenon.This is consistent with the phenomenon that the optimal window of noise moves to a greater noise strength asrincreases in Fig.4(b).

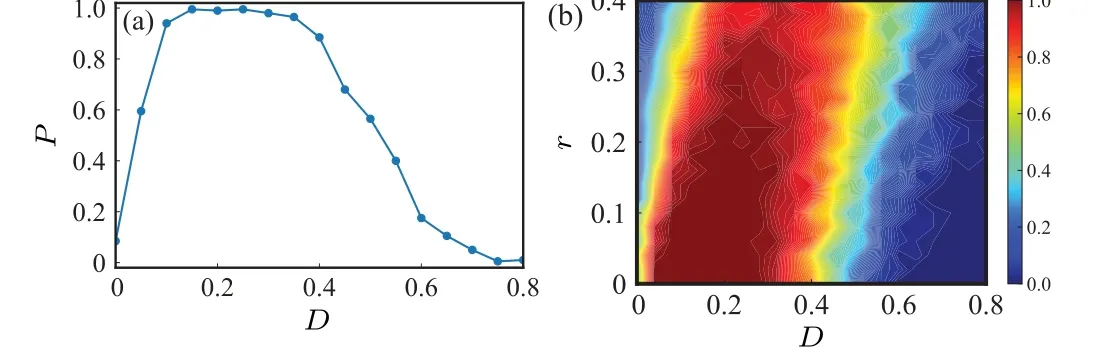
Fig.4.The variation of success probability P with different parameters in the bistable region: (a)noise intensity D for fixed r=0.2; (b)D and bifurcation parameter r.The system appears to have an optimal window of noise that displays resonance phenomenon with a single flat peak as the noise strength varies.The optimal window of noise decreases as r increases and moves to a greater noise strength.

To further investigate the effect of different parameters on LSR, we plot the variation ofPwith different parameters in Fig.4.Figure 4(a)illustrates the variation ofPwith noise intensityDfor fixed parametersr=0.2 andG=0.3.The results show thatPincreases rapidly with increasing noise strength for weak noise, and then stabilizes to 1.The system appears to have an optimal window of noise strength(0.100＜D ＜0.350).The logic response is nearly 100%accurate in an optimal window of the noise,so that the system reliably implements logic operations.As the noise strength continues to increase,the success probability gradually decreases until it tends to 0.The reason for this phenomenon is that the noise strength reflects the amount of energy provided to the particle by the external noise.When the noise strength is small, the energy provided by the noise is too small to support the particle crossing the potential barrier to make the leap between different wells,so that the system cannot produce reliable logic behavior.When the noise strength is too high,the energy provided by the noise is too high, which leads to frequent disorderly transitions between different wells and causes the particle to move in an irregular manner.Therefore, reliable logic behavior cannot be produced.Only when the noise is moderately strong does the energy provided by the noise allow the particle to cross the potential barrier to perform the correct transition behavior between different wells,producing reliable logic behavior.

Further, in Fig.4(b) we can find howPvaries with bifurcation parameterrand noise strengthD.In the figure, it

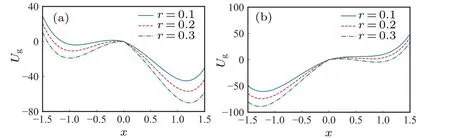
Fig.5.Generalized potential function at different bifurcation parameters r with G=0.3.(a) When I =0, the particle will be located in the right well under noise excitation.(b)When I=-0.8,the particle will be located in the left well under noise excitation.Clearly, the potential barrier increases as r increases.

Fig.6.The variation of transition rate k15 with noise intensity D and bifurcation parameter r in the bistable region.

3.2.Tristability

In the tristable region,in addition to the above logic gates,we can also obtain XOR/XNOR logic.We can obtain all the logic behaviors by defining different outputs.According to Table 2, we can set the output to logical 1 if the particle is in the right well and to logical 0 if it is in the others, for which we can obtain the AND logic gate.Likewise, we can obtain the other logic operations by defining the outputs.

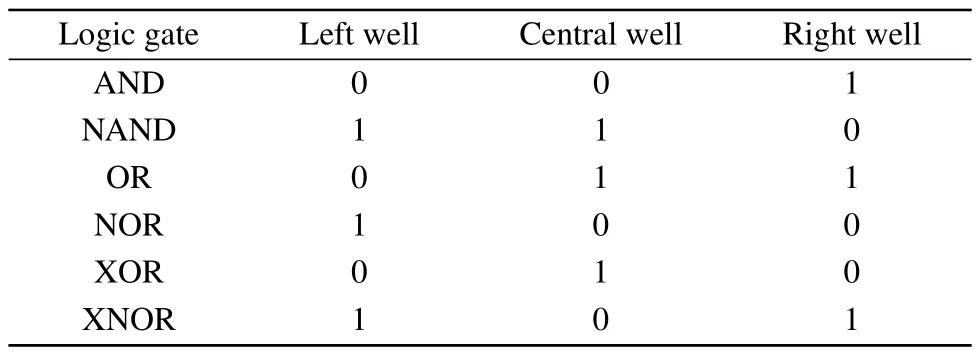
Table 2.For the six logic operations, the connection between the four input sets and the outputs.

For system (1), according to Novikov’s theorem and the unified colored noise approximation method,[41-43]the approximate Fokker-Planck equation is given by

Similar to the calculation in the bistable region, the expressions forT31andT35can be derived as

Since the pointx3is not involved in the approximation process forT13andT53,the expression can be obtained by the Gaussian approximation as

For the case of system(1)in the regionwe consider the logic input parameterKto take the value 0.4.Figure 7 displays the response of the system in Eq.(1) at different noise intensitiesDwhen the bifurcation parameterr=-0.35.For very weak noise (D=0.003), at some moments the particle cannot move to the desired well,for example[4000,5500],[10000,12000],[14000,14500].Therefore,the system cannot generate a reliable logic operation.For optimal noise(D=0.015),the system response yields a reliable logic operation.As the noise continues to increase(D=0.1),the particle transits frequently in the left and right potential wells when the logic input is 0.This LSR phenomenon is destroyed.Comparing with Fig.3,it can be found that the same phenomenon occurs in the tristable region as in the bistable region, where the presence of optimal noise intensity allows the system to produce reliable logic operations.However,the value of the optimal noise strength in the tristable region is much smaller than that in the bistable region.

Fig.7.The logic output x(t) with r = -0.35 corresponding to (a)D=0.003, (b) D=0.015, (c) D=0.1.The dashed red line indicates the logic input I,consisting of a combination of I1 and I2 which take the value-0.4 when the logic input is 0 and 0.4 when the logic input is 1.Clearly,when D=0.015,we can get the desired logic gate.

Further,Fig.8 illustrates the variation of the success probabilityPwith different parameters.In Fig.8(a) we plot the variation ofPwith noise intensityDfor a fixed parameterr=-0.35.It is found thatPincreases rapidly with increasing noise strength for weak noise, and then stabilizes to 1.The system appears to have an optimal window of noise strength(0.008＜D ＜0.026).In the optimal noise window, the logic response is nearly 100% accurate.The success probability gradually decreases as the noise strength increases, until it tends to 0.Compared with Fig.4(a), Fig.8(a) shows that the optimal noise value in the tristable region is much smaller than in the bistable region, and the optimal window interval for noise in the tristable region is also much smaller, indicating that the tristable region is more sensitive to noise.

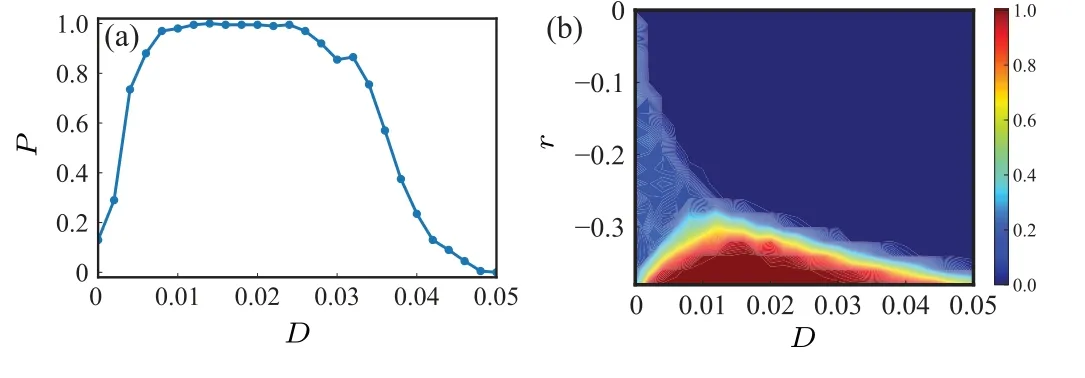
Fig.8.The variation of success probability P with different parameters in the tristable region: (a)noise intensity D for fixed r=-0.35,(b)D and bifurcation parameter r.When r ＜-0.33, the system produces a reliable logic response and the optimal noise interval becomes larger as r decreases.

To further analyze the variation ofPwithrandD, we plot Fig.8(b).It is found that the system cannot generate a reliable logic response when-0.33＜r ＜0.Whenr ＜-0.33,the system generates a reliable logic response and the optimal noise interval becomes larger asrdecreases.Figure 9 depicts the image of the generalized potential functionUgfor different values ofr.From the figure,it can be found that the height of the potential barrier is influenced byr.This shows that asrincreases, there is a subsequent increase in the potential barrier.Therefore, the higher the value ofr, the larger the noise intensity required to enable particle transition.However, for some high values ofr,the height of the potential barrier is too large to cause the particle to transit.Thus, it is impossible to generate a correct logic operation.Figure 10 shows that the range of moderate transition rates increases asrdecreases in the tristable region,which is consistent with the phenomenon in Fig.8(b).Comparing with Fig.4(b),we see that the range of values ofrthat can produce reliable logic operation in the tristable region is much smaller than in the bistable region,and that both the optimal noise values and the corresponding optimal noise interval range are much smaller.Comparing Figs.5 and 9,it is found that the potential barrier height in the bistable region is much higher than in the tristable region, so the bistable region needs a higher noise strength to make the particle transition.The potential barriers from the middle well to the two side wells are much smaller in the tristable region than the barriers in the bistable region, so a small noise may cause the particle to make frequent transitions when initiated in the middle well.Therefore, the optimal band of noise in the tristable region is narrower.Comparison of Figs.6 and 10 reveals that a smaller noise in the tristable region gives a moderate, optimum transition rate.Thus, the tristable region is more sensitive to noise.

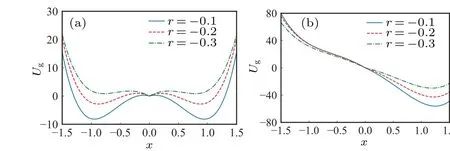
Fig.9.Generalized potential function at different bifurcation parameters r.(a) When I =0, the particle will be located in the middle well under noise excitation.(b) When I =0.8, the particle will be located in the right well under noise excitation.Clearly, the potential barrier increases as r increases.

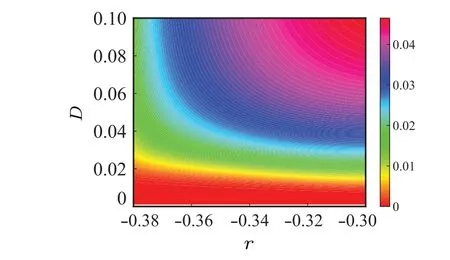
Fig.10.The variation of transition rate k15 with noise intensity D and bifurcation parameter r in the tristable region.

4.Conclusions

In this work,we investigate the logic operation of a crossbifurcation non-smooth system with bistable and tristable regions.By using Novikov’s theorem and the unified colored noise approximation method,we obtain the approximate Fokker-Planck equation and the generalized potential function to analyze the LSR phenomenon with numerical simulations.We numerically simulate the system’s logic operation in the bistable and tristable regions and perform a comparative analysis for the two regions.We show that the tristable region is more sensitive to noise than the bistable region.The optimal noise value in the tristable region is much smaller than that in the bistable region.Furthermore,the range of bifurcation parameters that can produce reliable logic output in the tristable region is much smaller,and the optimal noise strength range is smaller than in the bistable region.Similar results can be supported through the analysis of the generalized potential function and transition rate.We show in this work that tristability significantly enhances the transition rate.For example, this phenomenon is similar to the two-step nucleation mechanism in the crystallization of the protein lysozyme,where the intermediate stable state of proteins was found experimentally to accelerate the crystallization rate since tristability in two-step nucleation improves the transition rate and provides a powerful method of controlling the nucleation process.Similarly,the LSR mechanism in tristable dynamics is more sensitive than in bistable dynamics in the over-damped non-smooth system and can be utilized to implement more reliable logic gates in resonant tunneling diodes and simple circuits,and in monitoring weak targets in water degradation images and so on.Our results can be applied to relative experiments and help in selecting optimum parameters for actual implementations.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant No.12072262)and the Shaanxi Computer Society&Xiangteng Company Foundation.