Gray code based gradient-free optimization algorithm for parameterized quantum circuit
Anqi Zhang(張安琪), Chunhui Wu(武春輝), and Shengmei Zhao(趙生妹),2,?
1Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
2Key Laboratory of Broadband Wireless Communication and Sensor Network Technology(Ministry of Education),Nanjing University of Posts and Telecommunications,Nanjing 210003,China
Keywords: gradient-free optimization,Gray code,genetic-based method
1.Introduction
Parameterized quantum circuits (PQCs) offer a useful way to implement quantum algorithms[1–10]and can demonstrate quantum supremacy in the noisy intermediate scale quantum(NISQ)area.[11–15]PQCs are typically composed of fixed gates, e.g., controlled NOTs, or adjustable gates with phase rotations.Even at low circuit depth, some classes of PQCs are capable of generating highly non-trivial outputs.Usually, the parameter optimization in PQCs involves evaluation of the cost functionC(θ) from the quantum circuit and the computation of the cost function gradient ?C(θ) from the classical computer, where the barren plateau, in which the gradient of cost function vanishes exponentially with the size of system, is an important issue that needs to be carefully considered.[1,16]Various strategies have been suggested to tackle this issue.For instance, Skoliket al.[17]proposed a layer-wise learning optimization method where only a subset of all parameters is updated in each iteration.Additionally,clever parameter initialization and ansatz construction have been shown to enhance the stability and efficiency of training parameterized quantum circuits, thus preventing them from getting trapped in regions of vanishing gradients.[18–20]Nevertheless,further research is needed to assess the effectiveness of these strategies across different problem domains.Therefore,for large-scale parameter optimization problems,gradient-free optimization can be a preferable choice to avoid the barren plateau problem,which is promising for the devices in NISQ.For example,based on Gaussian process regression(GPR)and noisy expected improvement (NEI), a Bayesian optimization(BO)was proposed by Iannelliet al.[21]to provide an estimation of the ground state energy.An efficient method for optimizing the values of parameters by finding the direction and angle of rotation of quantum gates that yield minimum energy in PQCs was proposed by Ostaszewskiet al.[22]for variational quantum eigenvalue (VQE) tasks.However, these works are more effective for smooth optimization surfaces,they may lose their effectiveness for tasks with rough optimization surfaces in the presence of noise.In Ref.[23]the authors represented parameters using regular binary strings and performed iterative optimization within a genetic framework for parameter optimization.Nevertheless, the issue that minor parameter changes can trigger multiple bits to switch arises,causing significant step jumps throughout the optimization process.This phenomenon complicates the task of locating the global optimum.
In this work,we propose a Gray code based gradient-free optimization (GCO) algorithm for optimizing the parameters of parameterized quantum circuits (PQCs).First, for a given PQC, the parameter is encoded into a set of binary strings,called genes.Next, each individual gene is decoded using Gray code into decimal values, which are applied as parameters to the PQC for evaluation,obtaining corresponding cost values for fitness calculation.Then, the fitness values of all individuals are processed as probabilities when the roulettewheel selection strategy is adopted to prepare the parent population.Finally,the crossover and mutation operations are carried out to generate the offspring.The parameters in the PQC are optimized one by one until the cost value satisfies the stop conditions.
The proposed GCO algorithm offers several advantages:(1) The proposed GCO algorithm utilizes Gray code decoding techniques to optimize the parameters of PQCs,leading to improved optimization results for high-dimensional and nonconvex quantum circuit optimization problems,while avoiding the complexity of gradient computation.(2) The Gray code decoding method ensures that the parameters between two iterations only differ by one bit, helpful to avoid local optima in some optimization problems.Moreover,the proposed GCO algorithm enables the control of parameter precision by adjusting the number of bits in genes, which is particularly useful for quantum optimization tasks that require refining parameter values.(3)In the GCO algorithm,the roulette-wheel selection strategy is employed within the genetic framework to map fitness values to selection probabilities,enabling the selection of individuals with higher fitness as the parent population.Simultaneously,this strategy enhances offspring diversity and helps to prevent the algorithm from getting trapped in local optima.(4) The proposed GCO algorithm can optimize multiple parameters simultaneously,thereby the training time is reduced.
2.The Gray code based gradient-free optimization algorithm.
Figure 1 illustrates the framework of the proposed Gray code based optimization algorithm.The optimization process consists of the following steps.In step 1,a group of the initial population ofθmis generated randomly, where each individual is encoded as binary strings termed genes.Hereθmis them-th component of the parameter vectorθ.In step 2, all individuals of genes are decoded into decimals and evaluated in a fixed PQC which is selected according to the optimization task,to achieve cost values costmi(θ),respectively.In step 3,the fitness values are calculated according to the cost with the summation of all the fitness values to 1,and the fitness values are the probabilities to prepare the parent population by using roulette-wheel election strategy.In step 4, the crossover and mutation operations are performed on the parent population to generate the offspring.In step 5,the offspring is decoded and evaluated in the same PQC to check whether the minimum cost min[costm(θ′)] satisfies the stop condition.If the minimum cost does not satisfy the stop condition,updateθm+1;if the minimum cost satisfies the stop condition or the number of iterations is reached, the optimization process is stopped and the optimal parametersθ*are achieved.
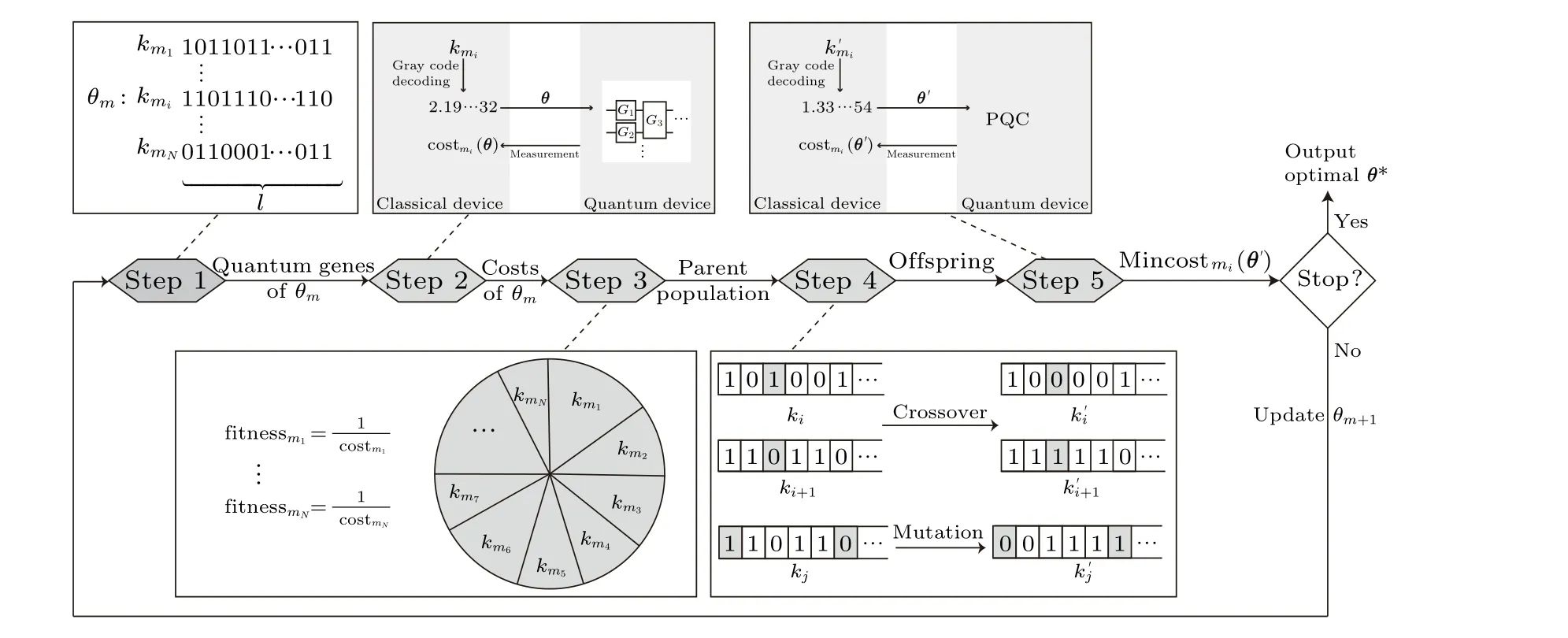
Fig.1.The framework of the GCO algorithm for optimizing parameters in PQC.
The proposed algorithm is detailed in the following.
(1) Generation of genes forθmAssume that theθmofθis optimized at the moment.In our proposed algorithm,θmis represented byNbinary Gray code strings which are randomly generated using a classical device in step 1 of Fig.1 askmi,i=1,...,N,each is called a gene.The number of bits in a gene is determined by the precision of the corresponding decimalθm, and the number after the dot specifies the precision.The range of parameters for a quantum gate is[-π,π].To set the precision of a decimal parameter ton, the number of bits required in genes isl,and their relationship can be expressed
as
therefore,lcan be
(2)Evaluation of individualsAll genes ofθmare evaluated in the quantum device to achieve the cost values.
As shown in step 2 of Fig.1,the genekmiis decoded into decimal value using Gray code and then loaded into the quantum device.Quantum devices in which the quantum gatesGpossess parameters can be referred as parameterized quantum circuits(PQCs).Therefore, when the types of quantum gates are fixed, the result of PQC depends on the parameter vectorθ.The circuit of PQC is determined by the specific optimization task,and as a result,the cost function is also dependent on the optimization task.In the case of a classification task, the optimization typically involves the preparation of the output quantum state of the PQC,denoted asφout,to a particular target quantum state,denoted asφopt.The cost is then calculated by using the fidelity-based approach,
(3) Selection of parent population In step 3 of Fig.1,the parent population is generated using the roulette-wheel selection[24]sampling strategy.The roulette-wheel selection is a method of sampling with replacement based on the probabilities assigned to each individual.This means that the same individual may be sampled more than once,and the higher the likelihood of an individual,the more times it may be sampled.The fitness values of each individual are determined using the cost values obtained in step 2 as follows:
where costmiis theith cost value estimated.Then the fitness values are processed so that all values are equal to 1 by the softmax function as
The parent population is prepared based on their processed fitness values until the sample size reaches the maximum population, as illustrated in step 3 of Fig.1.The processed fitness values are mapped into a circle and the size of area in the circle is corresponding to the probability of selecting individual,kmi,i=1,...,N.As shown in step 3 of Fig.1,km1with the largest size of area in the circle is more likely to be selected;whilekmNwith the lowest probability is less to be selected.
(4) Crossover and mutation operations The crossover strategy and mutation strategy are presented in step 4 of Fig.1.
Crossover The two adjacent parents are grouped together, and each bit position of gene is traversed separately.For each bit position,a bit swap with a certain probability may occur between the two adjacent parents.As illustrated in step 4 of Fig.1,the first 6 bit positions of genes of the two adjacent parents,denoted bykiandki+1,are presented.When traverse at the 3rd position,kiandki+1occur in bit swap.
Mutation Each bit of any gene in the parent population is traversed and may undergo a 0–1 transformation with a certain probability.As illustrated in step 4 of Fig.1,each bit position ofkjis traversed, and 1 to 0 transformation occurs at the 1st bit position and 0 to 1 transformation occurs at the 6th bit position.
(5) Evaluation of offspring In step 5, all genes of the offspring are evaluated in the same PQC as step 2 to achieve cost values.Then the minimum cost value, denoted by min(costm(θ′)),is selected and checked to determine if it satisfies the stop condition.If the minimum cost satisfies the stop condition, the iteration is stopped, and the optimal parameter vector, represented asθ*, is outputted.If the minimum cost fails to satisfy the stop condition, the next component ofθ,θm+1,is updated,and the optimization process is repeated.
The processes of the GCO algorithm are shown as algorithm 1.

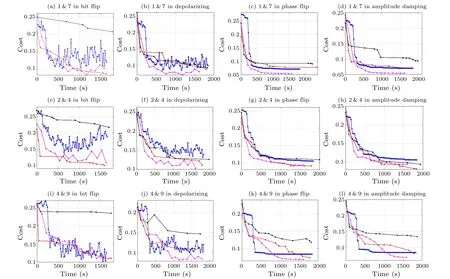
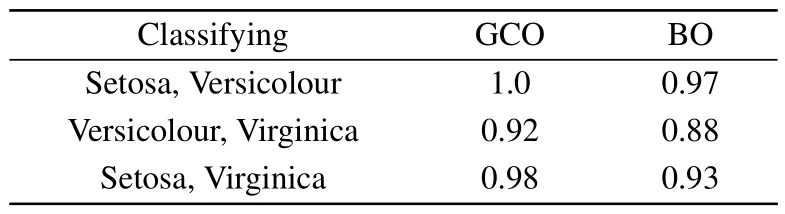
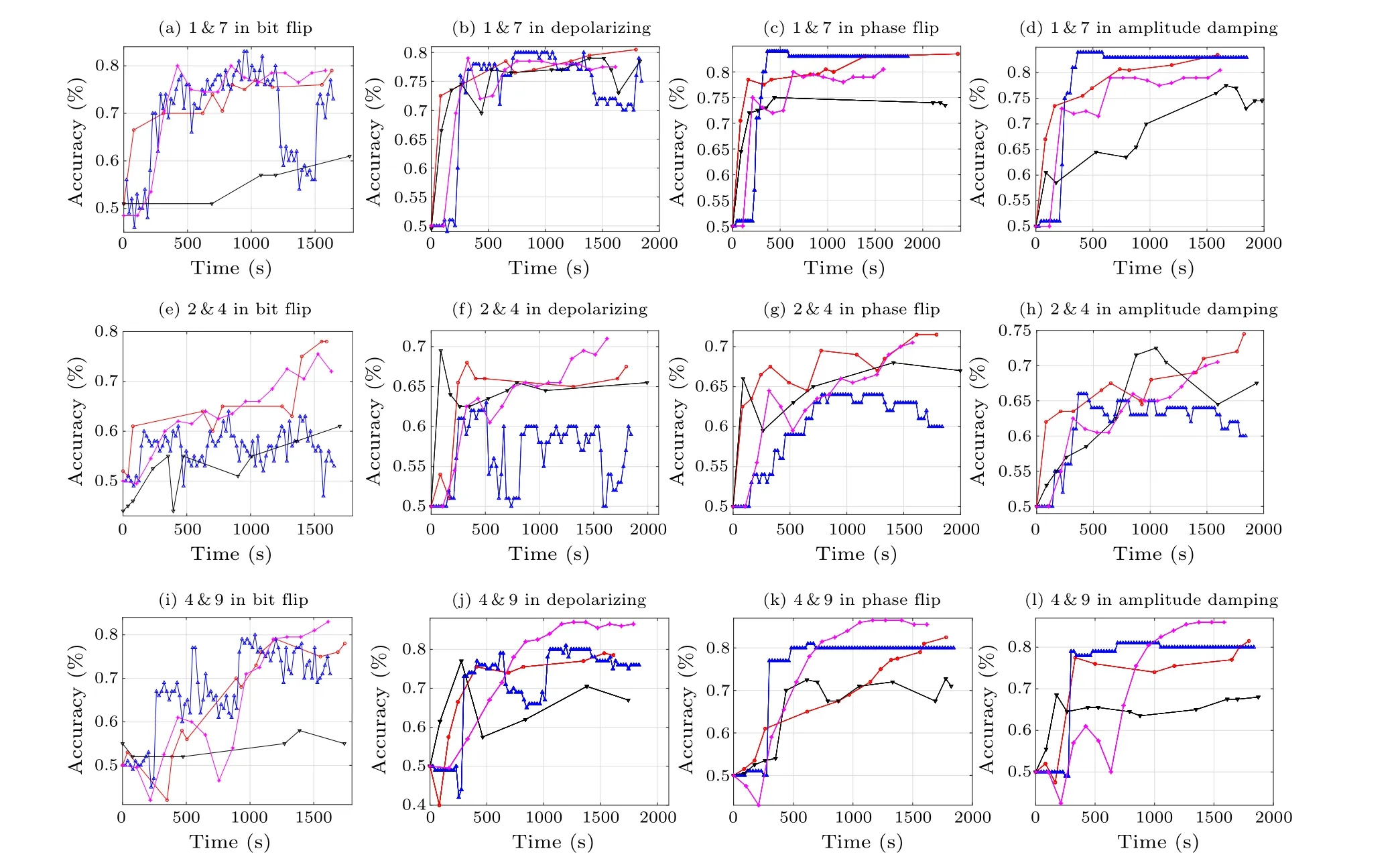
Algorithm 1 The Gray code optimization algorithm Require: Initialize the parameters in the PQC randomly;calculate the number of bits used l according to the precise of parameters n;a stop condition 1.loop 2.Calculate the value of cost function as cost-now 3.for m=1 to M 4.Generate N bit strings of θm randomly,in which each individual has l bits Evaluate the cost of each individual Fitness is calculated by using cost values achieved from step 2 and processed as the probabilities of the roulette-wheel selection sampling strategy to sample the parent population Crossover and mutation are carried out in the parent population to achieve the offspring Evaluate the cost of each individual in the offspring and record the minimum value of costs,min(costm(θ′)),as cost-min 5.if cost-min In this section,the feasibility of the proposed GCO algorithm is demonstrated through classification tasks on Iris and MNIST datasets, which are commonly employed in machine learning and deep learning. To compare the performance of the proposed GCO algorithm,Bayesian optimization(BO)algorithm,[21]binary code based optimization (BCO) algorithm,[23]and an adam-based optimization method, are simulated simultaneously.In this work, the BCO algorithm is almost identical to the GCO algorithm, with the only difference that BCO uses regular binary conversion when decoding from binary to decimal while GCO utilizes Gray code decoding.Gradient-based parameter optimization is the mainstream optimization approach in machine learning.In this simulation, the results of adam-based method are used as a benchmark, facilitating the understanding of the strengths and limitations of the proposed GCO algorithms.The simulations were realized by the PennyLane[25]module in Python.In the training processes, the number of gene bits for the parameters is 10.The probabilities of crossover and mutation are 0.3 and 0.05, respectively.There are 30 circles of all parameters that are trained at one time during the training process for GCO,BO and BCO,15 circles for the adam-based method.The classification tasks of Iris are achieved in the environment without noise, and the tasks in MNIST are achieved in the environment with four typical quantum noise,[26]i.e., bit flip, depolarizing, phase flip, and amplitude damping,under a probability of 5%.In Pennylane,noises are modeled as unitary operation and introduced into the PQC.The PQC we use[27]for the quantum classifier is shown in the Fig.2, two registers are contained in the PQC,A and B, which are used to store the training data and corresponding labels, respectively.During the training process,the training data of two datasetsX1,X2and parametersθare input into the register A, while the labels are input into the register B.The training objective is to ensure that the quantum state of register A forms the same as of register B, that is,U(X1,θ*)|0〉A(chǔ)=|0〉A(chǔ)andU(X2,θ*)|0〉A(chǔ)=|1〉A(chǔ),thus the PQC trains data of two datasets simultaneously by creating a unique mapping between the training data and the labels.After training,the final state of the PQC is|00〉A(chǔ)B+|11〉A(chǔ)B.The quantum gateCU(Xi,θ)is composed of multiple controlledphase gates,and each controlled-phase gate contains one component of the training data and parameter vectors.As a result,the depth of the PQC is dependent on the dimensionality of the training data vector. Fig.2.The parameterized quantum circuit(PQC)for classification tasks(a)and the details for uploading training data Xi and parameter θ into the PQC(b),where Xi=(x1,x2,...,xn)and θ=(θ1,θ2,...,θn). Fig.3.The cost value against the time for the three classification tasks in four types of noise by using GCO (red), BO (blue), BCO (black), and the adam-based method(pink)algorithms. Table 1.The accuracy by using GCO and BO for Iris dataset. For Iris dataset, we discuss the performance of the GCO and BO algorithms.Here, 40 training samples and 10 testing samples are randomly selected from each class,with three different subsets used.Specifically, the PQC for the classification task on the Iris dataset consists of 2 qubits with 10 serial controlled quantum gates.The numerical experiments are conducted five times, and the average results are listed in Table 1.From Table 1,it is obvious that the GCO algorithm outperforms the BO algorithm in terms of accuracy for all three subsets of the Iris dataset. For MNIST dataset, we randomly select 2000 training samples and 500 testing samples for each class,which are subsequently resized into 16 dimensions.Specifically, the PQC for the classification task on the MNIST dataset consists of 2 qubits with 34 serial controlled quantum gates.To evaluate the performance of three optimizing algorithms, we perform numerical simulations on the classification tasks for both similar handwritten digits (1&7) and difficult-to-recognize digits(2&4 and 4&9). The results of the proposed GCO, BO, BCO and adambased algorithms for the three classification tasks 1&7, 2&4,and 4&9, are evaluated in terms of cost value against time in Fig.3.In comparison to the BO,BCO and adam-based algorithms, the GCO algorithm maintains the ability for continuous convergence during the training process for four types of noise.It hints that the GCO algorithm is robust and has some resistance to the noisy environment.While the BO algorithm only has good robustness against phase flip and amplitude damping noises, the BCO algorithm exhibits both lower convergence capability and poorer robustness compared to the BO and GCO algorithms.The adam-based optimization method fluctuates in bit flip and depolarizing noises and shows good performances in phase flip and amplitude damping noises.However, overall, the adam-based method consistently converges,indicating robustness to four types of noises. Fig.4.The classification accuracy against the time respectively for the three classification tasks in four types of noise by using GCO(red),BO(blue),BCO(black),and the adam-based method(pink)algorithms. The classification accuracies of the GCO,BO,BCO and adam-based algorithms against time during the training process are shown in Fig.4.In comparison to the BO, BCO and adam-based algorithms, the GCO algorithm consistently demonstrates enhanced classification accuracy regardless of the noise type.Notably, the GCO algorithm achieves accuracy levels of around 0.8 for the 1&7 task, over 0.7 for the 2&4 task, and around 0.8 for the 4&9 task.It indicates the effectiveness of the GCO algorithm in noisy environments for the three classification tasks.Conversely, the BO algorithm’s performance is influenced by both the classification task and the specific noise type.It exhibits significant accuracy fluctuations when subjected to bit flip and depolarizing noise environments.Moreover,in comparison to the 1&7 and 4&9 tasks,the BO algorithm achieves lower accuracy in the 2&4 task,reaching below 0.65.Meanwhile, the BCO algorithm consistently shows poor accuracy performance across various noise types and classification tasks.The adam-based optimization method shows less improvement in the early stages of training processing in environments with four types of noise,but it eventually achieves higher classification accuracy than other optimization methods.Additionally, in some classification tasks, such as the task 4&9,it can achieve higher accuracy.This is due to the fact that gradient-based optimization methods are better suited for searching within local regions, allowing for more precise parameter optimization values. In this work, we have proposed a GCO algorithm for a parameterized quantum circuits(PQCs).The parameters in a PQC are expressed as binary strings and are decoded in Gray code way to keep Hamming distance.In the training process,an genetic-based method is adopted to generate the next generation so as to update the parameters of the PQC iteratively.One parameter is optimized in each iteration, so that the proposed GCO algorithm has a shorter time for optimization.Furthermore, we simulate the GCO algorithm for classification tasks in two datasets,and compare the results with those using the BO algorithm and the GCO algorithm.The simulation results show that the GCO algorithm has a good ability to resist the noises and makes better optimization performance in the optimizing processes, both for the similar handwritten digits and the difficult-to-distinguish handwritten digits. Acknowledgments This work was supported by the National Natural Science Foundation of China (Grant Nos.61871234 and 62375140),and Postgraduate Research&Practice Innovation Program of Jiangsu Province(Grant No.KYCX190900).3.Result and discussion

4.Conclusion
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

