Quantum synchronization with correlated baths
Lei Li(李磊), Chun-Hui Wang(王春輝), Hong-Hao Yin(尹洪浩),Ru-Quan Wang(王如泉),?, and Wu-Ming Liu(劉伍明),§
1School of Physical Science and Technology,Inner Mongolia University,Hohhot 010021,China
2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
Keywords: quantum synchronization,entanglement,quantum coherence,nonequilibrium reservoir
1.Introduction
Synchronization is a universal phenomenon that is widespread in natural and social sciences.[1,2]In physical systems,one of the synchronization emerges spontaneously without an external driver, is called spontaneous synchronization, instead, is forced synchronization, also known as entrainment.In classical systems, synchronization has been studied extensively.[3]And it has recently attracted much attention in the quantum regime,[4]where both spontaneous synchronization[5–19]and entrainment[20–27]have been explored in a variety of systems including spins, and harmonic and nonlinear oscillators.Significance of quantum synchronization have also been recently reported in experiments.[28,29]
Dissipation, either global or local, is known to induce synchronization among quantum oscillators and spins, either in the steady state or in the transient relaxation dynamics.[30]Quantum synchronization of spin that interacting collectively with a common dissipative environment have been carried out,recently.[5,12,18,31,32]However, only a very limited number of studies have been reported on the local dissipation induced quantum synchronization.Especially we have not seen any reports about the effect of locally nonequilibrium reservoir on synchronization.
Quantum correlation is one of the key resources for quantum information processing and quantum technologies.[33–36]Spontaneous mutual synchronization emerges as a result of some temporal correlation between the local dynamics of the subsystems of the system of interest.And certain well-known measures of quantum and total correlations contained in the global system, e.g., entanglement, quantum discord, and mutual information,have been explored to pinpoint their relation to the emergence of mutual synchronization between the local evolution of the subsystems.[4]Indeed, there exists no general connection between the onset of synchronization and the behavior of correlations in the global system.For example,recently Karpatet al.have shown that correlations in the global system play no relevant role for the dynamical synchronization of local observables by means of a collision model.[16]Lastly, the relationship between quantum coherence and synchronization has also been studied in a bioinspired vibronic dimer system.[37]
In this paper, we consider the effect of nonequilibrium reservoir on quantum synchronization of system spins, including the influences of quantum correlation and coherence of reservoir.We propose a framework based on collisional models,[38–59]which allows us to analyze the quantum effect of reservoir in the functioning of quantum synchronization of system.Our setup,depicted in Fig.1,consists of two system spinsSAandSB.Each of these is in contact with a reservoir modeled by the repeated interaction of ancillas.These ancillas are first prepared in a state with coherence at effective temperaturesT1andT2, respectively, and then undergo a unitary evolutionU, which correlates them before their interact with the systemsSAandSB.We study if, and how the synchronization of system can be affected by the quantum correlation and coherence of reservoir,and which one is the key to affect quantum synchronization.
The manuscript is organized as follows.In Section 2,model and figures of merit are introduced.In Section 3 we study the effect of nonequilibrium reservoir on intrasystem synchronization in detail,and the conclusions are given in Section 4.
2.Model and figures of merit
2.1.Model
We consider the system to be composed of two coupled qubits described by theXXZHamiltonian
whereJ,?,andBiare the interaction strength,anisotropy and local magnetic field, respectively.The operatorsσxi,σyi,σziare the Pauli matrices for the qubiti(i=1,2).As[Sz,HS]=0(Sz=σz1+σz2),the total magnetization is a conserved quantity.Notice that we set ˉh=kB=1 throughout this paper.
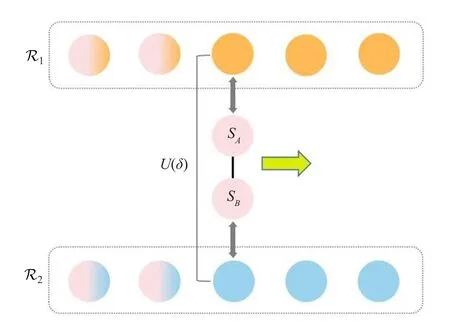
Fig.1.Sketch of the protocol: a pair of ancillas come from reservoir ?1 and ?2 respectively, collide to each other under a unitary operation U(δ).Then this correlated ancillas in the global state ρE (Eq.(5))collide with the system’s spins SA and SB.
We assume that each qubit of the system interacts with two reservoirs?1and?2respectively,and each reservoir consisted of a stream of uncoupled qubits(we call ancillas)whose logical states are{|0〉,|1〉}.The interaction between the system qubit and a ancilla only lasts for a short timeτduring which the interaction Hamiltonian is given by
where the operators ?σji(j=x,y,z)are the Pauli matrices for a ancilla interacting with the system qubiti.The coefficientγdetermines the strength of the interaction.Additionally each ancilla is subject to the local Hamiltonian
wherei=1,2 andHE=HE1+HE2.
2.2.Quantum synchronization
Spontaneous quantum synchronization between a pair of quantum systems can be said to emerge through the establishment of coherent oscillations in the expectation values of their local observables, and it is generally possible to observe this behavior by just looking at the dynamics of these expectation values.We adopt the well-known Pearson correlation coefficientC12,which is a standard tool in statistics for identifying correlations between two data sets, as our figure of merit for the detection of synchronous behavior.[4]Given two discrete variablesxandy,linear correlation between them can be measured by the Pearson coefficient,which is given as
where ˉxand ˉydenote the averages ofxandyover the data sett.C12is a bounded function which satisfyC12∈[-1,1].WhileC12=0 indicates that the two variables are completely uncorrelated,C12=1 andC12=-1 points out a full positive and negative linear correlation,respectively.In our work,the variables in question are the expectation values of the local observables of the system qubitsSAandSBin thexdirection,namely,Consequently, based on the definition of the Pearson coefficient[Eq.(4)],completely positive and completely negative correlations imply fully synchronized and fully antisynchronized behaviors between the local expectation values, respectively.As we sampleC12over a sliding data window along the total evolution time, we can obtain a time-dependent Pearson coefficient to probe how the oscillations become phase locked over time.And to get a smooth behavior in the Pearson coefficient evolution,we allow the adjacent data windows to partially overlap for a certain interval.
2.3.Repeated interactions
In order to investigate the effect of reservoir on quantum synchronization between two qubits of system, we correlate the ancillas with a unitary transformationU, and their state becomes

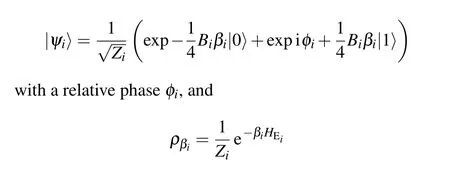
wherepi ∈[0,1],is the thermal state.Hereβi=1/TiandZi=Tr[e-βiHEi]are the inverse temperature and the partition function, respectively.Notice that the diagonal elements of statesρEiandρβiare identical, and compared with the thermal state, the off-diagonal elements of stateρEiare nonzero ifpi ?=0.In this case the effective temperature of the reservoir is defined by its diagonal elements.
We assume that the unitaryUin Eq.(5) correlating the ancillas of reservoir is a partial swap operation

Whenδ=0 equation(9)is reduced into an identity operator and indicates that there is no interaction between two ancillas;and whenδ=π/2 equation (9) is reduced into a fully swap operator and represents a complete exchange of quantum state information between them.
3.Quantum synchronization
In the following,we investigate the roles of quantum correlation of reservoirs on synchronization behaviors between system spins.We suppose that the pair of system spins is uncorrelated initially,i.e.,

3.1.Thermal state
Firstly we consider initial thermal states of two reservoirs,i.e., Eq.(8) withpi=0, and the density matrix of two ancillas after the unitaryU(δ) becomes Eq.(A2) in Appendix A.From the numerical calculation, we find that even though the Pearson coefficient can eventually approaches 1 with a long enough evolution time,the expectation values of the local observables become extremely small.In other words,the system has reached its steady state before the transient synchronization appears.Therefore in this case even though the Pearson coefficient can arrive at 1 finally,there is no visibility for this synchronization.Based on this, when the Pearson coefficient has not reached 1 before the expectation value of the local observable decays to 10-4of the initial value,we say that the two qubits can not be synchronized.It is worth emphasizing that the magnitude of this value makes no qualitative difference to the following results in this paper.In order to investigate the roles of quantum correlation of reservoir on synchronization,we calculate the entanglement between the two ancillas after the unitaryU(δ).It shows that the entanglement is always zero,and the full details are given in Appendix A.
3.2.State with coherence

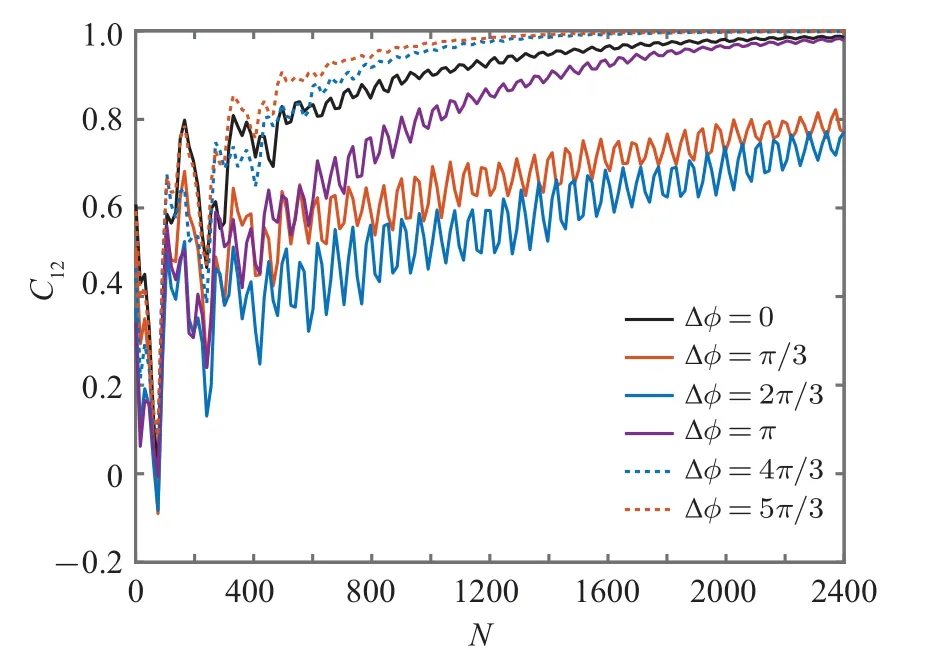
Fig.2.Pearson coefficient C12 in terms of the number of collisions N for initial state (8) with p1 = p2 =0.9 and different phase differences ?φ[?φ =0,π/3,2π/3,π,4π/3,5π/3], which is plotted for data windows of 140 collisions with partial overlaps of 125.Parameters: J =0.1, ?=1,B1/B2=1.2,T1=2T2=2,γ =0.3,and δ =π/32.
In Figs.3(a)–3(c),we display the final value of the Pearson coefficientC12after 2400 collisions taking place between the system and the reservoir particles in terms of the phase difference ?φ,figure 3(a)is in the weak coupling regime withδ=π/32, figure 3(c) is in the strong coupling regime withδ=π/4,and figure 3(b)is an intermediate case withδ=π/8.
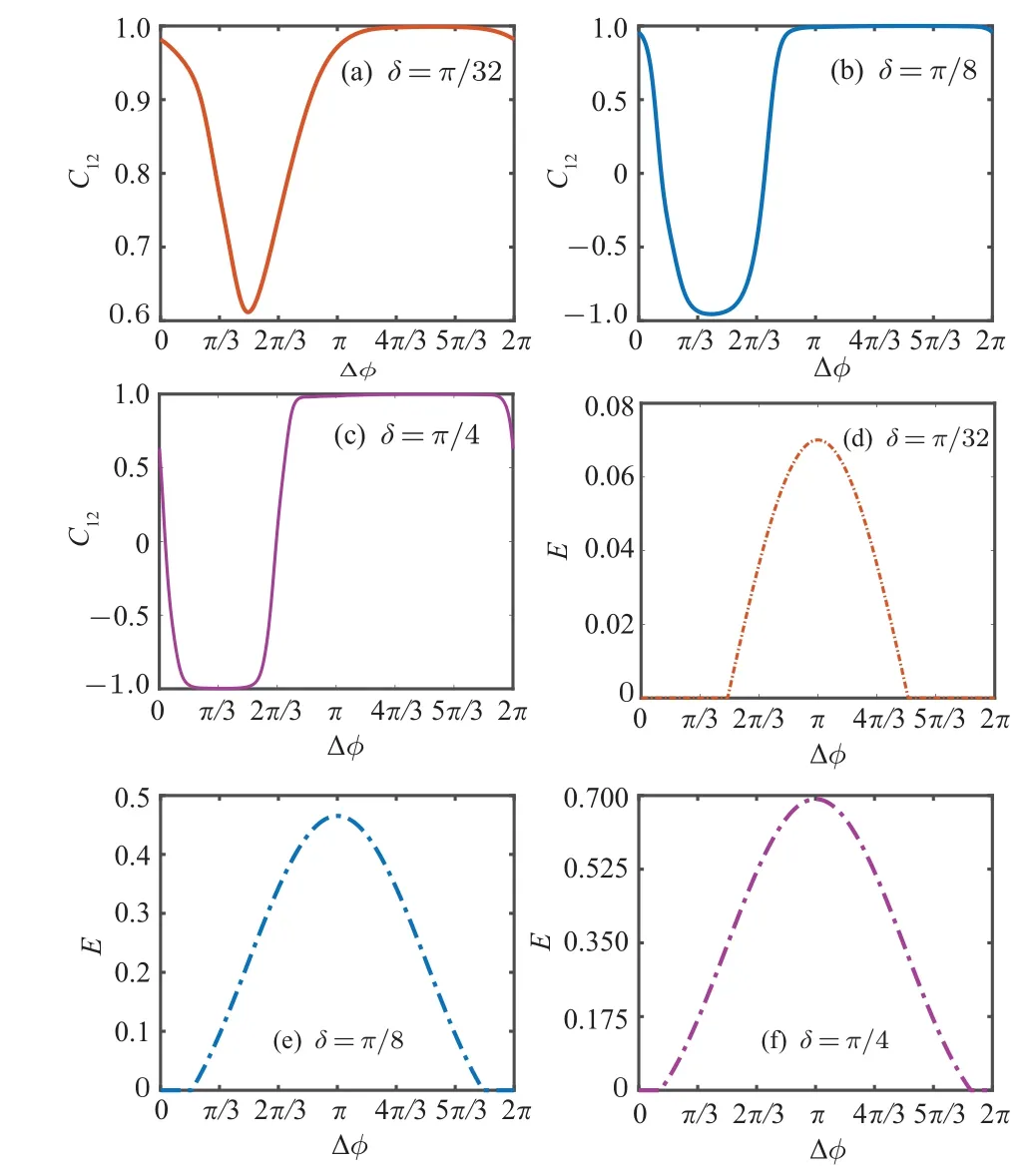
Fig.3.(a)–(c) Synchronization diagram displaying the final value of the Pearson coefficient C12 after a time interval of N =2400, as a function of the phase difference between two ancillas [?φ], in the weak (δ =π/32)-and strong (δ =π/4)-coupling regimes for panels (a) and (c) respectively,and δ =π/8 which results in an intermediate case for panel (b).(d)–(f)Quantum entanglement between the two ancillas [Eq.(A1)] as a function of ?φ, in the weak (δ =π/32)- and strong (δ =π/4)-coupling regimes for panels (d) and (f) respectively, also δ =π/8 is an intermediate case of panel(e).For all plots the other parameters are the same as those in Fig.2.
Also the phase difference can influence the time for system spins to get synchronized.And the synchronization–antisynchronization transition between system spins can be realized by manipulating ?φin the strong coupling regime(Fig.3(c)).Physically, this can be easily understood as follows.As all four qubits(system+two ancillas)are interacted after state preparation,thus if one scans the phase difference of the ancillas would change the phase difference of the system,and two system qubits are in synchronization(the phase difference between two system qubits is 0)or anti-synchronization(the phase difference between two system qubits isπ).As mentioned above,the synchronization behaviors show a much stronger response in the strong coupling regime in contrast to the weak coupling regime.In order to investigate this in detail,we calculate the entanglementEbetween the two ancillas after the unitaryU(δ)as a function of ?φ.Figure 3(d)(δ=π/32)and figure 3(f) (δ=π/4) are the weak- and strong-coupling regimes respectively, and figure 3(e) is an intermediate case withδ=π/8.It can be seen that the range of synchronization and the speed of the establishment of synchronization can be improved with the increase of entanglement.Thus,we clearly demonstrates an example of the dynamical establishment of reservoir entanglement-induced spontaneous mutual synchronization in spin chain locally coupled to two independent environments.In all,we can control the synchronization behaviors of system spins by manipulating the phase difference between two reservoirs and the quantum entanglement of reservoir.
In Fig.4(a), the final value ofC12after 3500 collisions between the system and the reservoir particles is shown as a function of left bath temperatureT1, atT2=1 for different phase differences (?φ= 2π/3,π,4π/3).We show that increasing the temperature gradient,T1-T2,speeds up the emergence of synchronization between system spins for fixed ?φ.In Fig.4(b),we present the entanglement between the two ancillas of reservoir(Eq.(A1))as a function ofT1.As expected,the entanglement is increased with the increase of temperature gradient.In other words,the entanglement of reservoir has an essential impact on the establishment of synchronization between system spins.
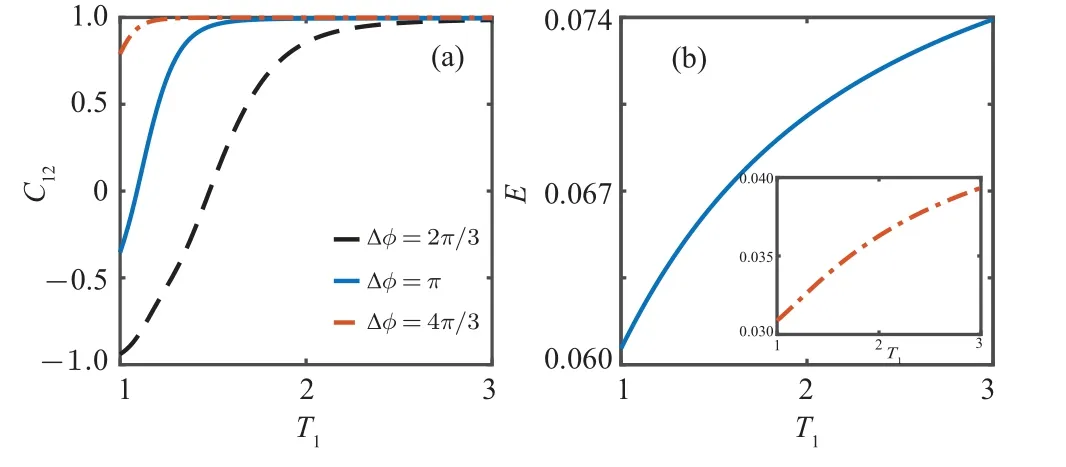
Fig.4.(a)Synchronization diagram displaying the final value of the Pearson coefficient C12 after a time interval of N =3500, as a function of left bath temperature T1,at T2=1 for different ?φ.(b)Quantum entanglement between the two ancillas [Eq.(A1)] as a function of T1, with ?φ =π (the blue solid line)and ?φ =2π/3,4π/3(the red dot–dashed line).For all plots the other parameters are the same as those in Fig.2.
4.Conclusion
In this paper,we have investigated the nonequilibrium effects of reservoir on quantum synchronization of the system.We have considered two-qubitXXZchain coupled independently to their own reservoirs,and the reservoirs are modeled by the so-called collisional model.In our framework, two reservoir particles, initially prepared in a thermal state or a state with coherence.In order to investigate the roles of quantum entanglement of reservoir, we have correlated two reservoir particles through a unitary transformation and afterward interact locally with the two quantum subsystems.For initial thermal states of two reservoirs,it has no synchronization and the quantum entanglement of two reservoir particles is zero.However, for the initial states of two reservoirs with coherence, the synchronization between system spins can be controlled by manipulating the phase difference and the quantum entanglement between two reservoir particles.And the degree of synchronization and the speed of the establishment of synchronization have be improved with the increase of entanglement.It means quantum entanglement of reservoir is the key of controlling quantum synchronization of system qubits.We expect that these properties revealed in this paper can help one to gain some insight into the connections between entanglement and quantum synchronization.
Appendix A
For the initial states of two reservoir particles with coherence (Eq.(8)), the density matrix after the unitaryU(δ) can be expressed as
where
Here we letβ2=1,φ2=0,B1/B2=1.2, andp1=p2.For initial thermal states of two reservoirs (p1=p2=0) withβ1=β2/2=1/2,equation(A1)becomes
Acknowledgments
Project supported by the National Natural Science Foundation of China(Grant Nos.12147174 and 61835013)and the National Key Research and Development Program of China(Grant Nos.2021YFA1400900,2021YFA0718300,and 2021YFA1400243).
All the authors would like to thank Prof.Jian Zou and Dr.Kun-Jie Zhou for fruitful discussions.
- Chinese Physics B的其它文章
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution
- Characteristics of cell motility during cell collision

