Analytical solution to incident angle quasi-phase-matching engineering for second harmonic generation in a periodic-poled lithium niobate crystal
Li-Hong Hong(洪麗紅), Ya-Ting Qiu(邱雅婷), Xiao-Ni Li(李曉霓),Bao-Qin Chen(陳寶琴), and Zhi-Yuan Li(李志遠(yuǎn)),?
1State Key Laboratory of High Field Laser Physics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China
2School of Physics and Optoelectronics,South China University of Technology,Guangzhou 510640,China
Keywords: nonlinear frequency conversion,transmission,reflection,lithium niobate
1.Introduction
Laser has a limited wavelength range since it has been invented.[1]Due to the discovery of second-harmonics generation (SHG), the boom of nonlinear optics was opened.The interaction of laser light with diverse nonlinear crystals,[2–6]leading to various nonlinear optical processes such as SHG, sum-frequency generation (SFG), difference-frequency(DFG),and others,offers a powerful and versatile way to generate new optical frequencies and provides a wealth of possibilities to expand the wavelength range of lasers.For the process of SHG,the dispersion of nonlinear media makes the fundamental wave (FW) and the second-harmonic wave (SHW)have different phase velocities in the dielectric material of nonlinear crystal, resulting in a phase-mismatching.To satisfy the phase matching conditions, the birefringence phase matching (BPM)[7,8]and quasi-phase matching (QPM)[9–16]technologies have been explored and become two commonly used technical methods.Compared with the limitations of BPM, QPM is more preferred by virtue of its high nonlinear susceptibility tensor, flexible nonlinear medium selection, as well as various tuning methods,which can compensate phasemismatching by modulating the sign of nonlinear coefficients.As an attractive nonlinear optical material, lithium niobate(LN) crystal possesses some superior features such as excellent nonlinear optical properties, broad transparency range,and more uniquely, capability to build microstructures with ferroelectric domain inversion that enables QPM.[17,18]Many second-order nonlinear effects[19–25]have been fully developed within the LN nonlinear crystals including periodic poled lithium niobate (PPLN) crystal.Recently, people have realized the specific-wavelength SHG output by the PPLN crystal,and the broad-band SHG output via the chirped periodic poled lithium niobate (CPPLN).It is also worth mentioning that in recent years,with the rapid development of thin film technology on lithium niobate insulators and related surface micronano manufacturing technology,lithium niobate has been used to achieve a series of miniaturized, integrated, high-quality,high-performance photonic functional devices.[26–30]
The physical understanding of various nonlinear optical processes in LN crystals involve solution of transport of FW within LN crystal, its excitation of SHW, the transport of SHW, and the mutual interaction and coupling between FW and SHW.The physics is a little bit complicated, and the corresponding mathematics is also some certain troublesome, especially when considering that LN crystal and many other nonlinear crystals are anisotropic materials rather than simple isotropic materials.There have existed some schemes that extensively only investigate the reflection and transmission of incident wave from isotropic medium to uniaxial crystal interface,[31–39]such as the classical electromagnetic theoretical analysis method.[37–39]However, the implementation of a specific SHG in PPLN crystal usually utilizes the collinear configuration where the pump FW light and generated SHW light beam is parallel.This geometric configuration has some limitations for expanding the nonlinear frequency conversion range.First, the pump light is normally incident upon the PPLN nonlinear crystals.In this case,QPM for a single wavelength that is designed to match the specific PPLN pitch size of inverted ferroelectric domains can be intelligently achieved,but not for other wavelengths, thus the bandwidth is limited.As far as we know, very rare reports were presented on the generation of narrow-band tunable SHG based on QPM technology via a PPLN crystal.
In this work, we theoretically investigate the noncollinear configuration of SHG via QPM in a PPLN crystal,where the pump light impacts the PPLN crystal surface at different angles,and explore a new way to expand the bandwidth of SHG for a single PPLN crystal via incident angle tuning.We calculate the reflection coefficient and transmission coefficient at air-crystal interface in LN crystal and derive the coupled-wave equations to describe the interaction between FW and SHW non-collinearly transporting in crystal.We analyze the phase mismatching when the light is incident at different angles,study the walk-off effect between the transmission FW and SHW in LN crystal, and investigate the accomplishment of QPM via the angle tuning in a PPLN crystal with first-order QPM structure at different pump laser wavelength.We wish to create a complete theoretical system to quantitatively evaluate the SHG process uncovering the reflection and transmission of pump light at the air-crystal surface across a wide range of incident angles at different incident pump wavelengths,and explore the possibility to realize narrow-band tunable lasers by simply controlling the incident angle in a PPLN crystal working in the framework of QPM technology.Surely,such a study should have an important practical significance in actual experiments and laser architectures.
study should have an important practical significance in actual experiments and laser architectures.
2.Principle of oblique incidence angle tuning for SHG
2.1.Theoretical model establishment and crystal interface analysis
In our physical mode, az-cut LN crystal is used as the nonlinear medium, and the schematic configuration is shown in Fig.1(a).The extraordinary crystalline axis of LN sample is along thezaxis, while its ordinary crystalline plane is coplanar with thexoyplane.We presume that a beam of TEpolarized pump light with electromagnetic field components(Ez,Hx,Hy)and the wave vectorkiis incident on the LN crystal surface from air at an angleαwithyaxis, and transports within thexoyplane.Further analysis with the specific illustration of the incident light at the interface of the two media(air and LN crystal)is displayed in Fig.1(b).As we know,the refractive indexn0,relative dielectric constantεr1and relative permeabilityμr1of air,the relative permeabilityμ1of crystal are all of values 1.The relative dielectric constantε1in this case is equal toεzin crystal for FW.In such a scheme, the pump light transmitted into the LN crystal is extraordinary light, and the refractive index of FW and SHW is defined asn1andn2respectively.The scheme we adopted guarantees the use of the maximum nonlinear polarization tensord33(about 27 pm/V)of the crystal,which is the most favorable configuration for driving an efficient nonlinear frequency up-conversion process and corresponds to the extraordinary refractive index surfaces of the crystal ellipsoid.Maximum spatial overlap of fieldE1zandE2zdistributions can be achieved.Therefore,the refractive indexn1of the FW and the refractive indexn2of the SHG refer to the refractive index of extraordinary light in the LN crystal.The angle of the transmitted FW wave vectork1with theyaxis isβ, and that of SHW vectork2with theyaxis isγ.Notably, we approximately regard the LN crystal as an infinite crystal,as in most textbooks of nonlinear optics.Considering the transmission and reflection of FW at the LN crystal front (first) surface, the crystal will be a semi-infinite crystal so that the influence from the back(second)surface can be neglected.
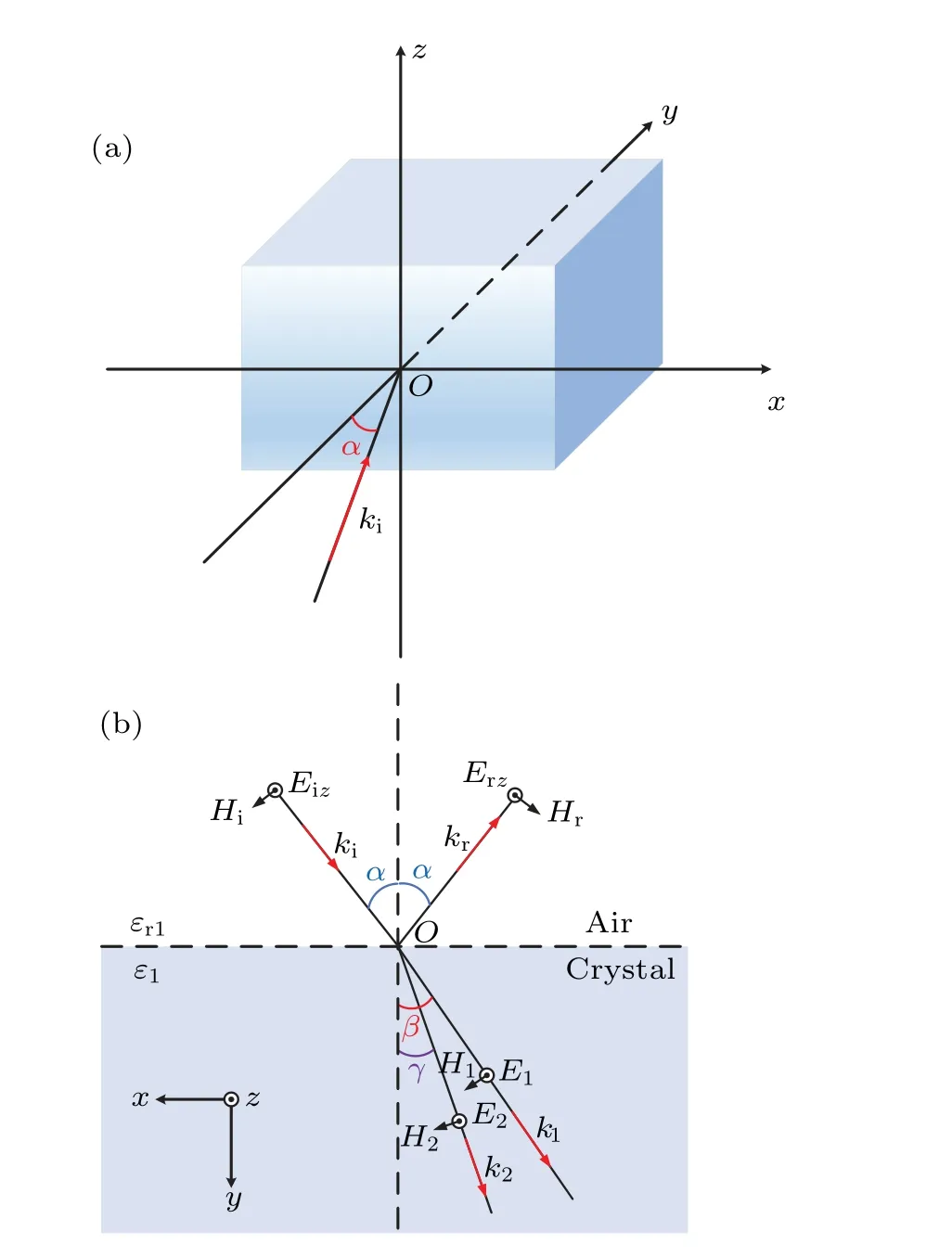
Fig.1.(a) Schematic configuration of a z-cut LN crystal in the air, a TEpolarized pump light reaches on the crystal surface in xoy plane at an angle α with y axis.(b)The cross-sectional view of the light propagations and electromagnetic field analysis of incident wave, reflection wave, transmission wave(FW), and SHW from air to LN crystal, responding to wave vectors ki, kr,k1(kt), k2, respectively. εr1 and ε1 are the relative dielectric constants of air and crystal for transmission wave(FW).α is incident(also the reflection)angles of FW,β and γ are the transmission angle of FW and SHW,respectively.
Here, the FW and SHW light involved are both electromagnetic waves so that all their physical and chemical properties are dictated by the space–time evolution of electromagnetic field.Therefore, we can conduct our analysis from the following set of Maxwell’s equations for a monochromatic incident FW light with angular frequencyω1,which are

2.2.Obliqueincidence nonlinear coupled wave theory for FW and SHW
In the reflection and transmission model of the air-crystal interface,we consider two nonlinear conversion processes simultaneously, including FW exciting SHW (ω1+ω1=ω2)and SHW coupling with FW (ω2-ω1=ω1) in LN crystal.Since the wave equations are used to describe the propagation and interaction of light waves in a general medium,we derive the nonlinear coupled-wave equations starting from the wave equations,which can be written as
wherePNL(ω1) andPNL(ω2) are second-order nonlinear polarizations, and they are new radiation sources of FW and SHW in LN crystal.E1andE2represent the electric fields for monochromatic wave at the angular frequencyω1of FW andω2of SHW in crystal.Note that these two electric fields have only thez-component polarization, so we can obtain the scalarPNL(ω1),PNL(ω2) from the nonlinear polarizationPNL(ω2)=P(2)(ω2)e-iω2t=?zε0χ(2)E1E1andPNL(ω1)=P(2)(ω1)e-iω1t=?z2ε0χ(2)E2E*1, where the second-order nonlinear susceptibility tensor isχ(2)=2d33for the general LN crystal.Further, the wave functions for the transmitted FW and SHW are supposed to be
whereE10,E20are the electric field amplitudes of FW and SHW, assumed to be varying slowly along theydirection.k1x,k2x,k1y, andk2ydenote the components of transmission FW vectork1and SHW vectork2in thexandydirections, which satisfyk21=k21x+k21yandk22=k22x+k22y.Thus we havek1x=k1sinβ=(ω1/c)n1sinβandk2x=k2sinγ=(ω2/c)n2sinγ.Considering the photon momentum conservation between incident FW light, transmitted FW light, and generated SHW light in thexdirection, we find 2k1x=k2x=2kix=2(ω1/c)sinαand the phase mismatching inxdirection can be written as
By substitutingE1,E2,PNL(ω1),PNL(ω2), ?kx, ?kyinto Eqs.(5)and(6),we eventually derive the coupled-wave equations for SHG in a general LN crystal in the case of the slowlyvarying amplitude approximation, which can be expressed in the following form:

For convenience, we refer to ?kyas the oblique-incidence phase mismatching, which closely relies on the incident angleαand the pump wavelengthλ1.
When the pump light strikes the nonlinear crystal with different incident angles, it can be noticed obviously that the propagation of FW and SHW wave vectorsk1,k2are noncollinear, due to the unequal anglesβandγcaused by the dispersionn1?=n2of the LN crystal.Spontaneously,the transmission of FW and generated SHW will encounter a walk-off effect.We define the walk-off distance from FW and SHW in thexdirection as walk-off length ?x=|xFW-xSHW|.Here,xFW=ytanβandxSHW=ytanγare the tangential position of FW and SHW light beam at the crystal length ofy,corresponding to different incident angleα.The walk-off length can be expressed by
According to Eq.(14), it can be intuitively observed that the walk-off length ?xis intrinsically controlled by the incident angle, the pump wavelength and the crystal length.After a simple calculation, we find that the walk-off length changes with incident angle and incident wavelength.
2.3.Rigorous solutions of oblique-incidence coupled wave equations in PPLN
The theoretical model described above for the reflection and transmission of pump light at the surface of an LN crystal and the coupling theory are also applicable to a PPLN crystal.Due to the phase mismatching caused by the dispersion between FW and SHW in general LN crystals,the PPLN crystal can effectively solve this problem with its own lattice structure via the QPM technique.Here,we select a PPLN crystal with first-order QPM structure to achieve a higher conversion efficiency.In this case,the PPLN crystal can provide an auxiliary reciprocal lattice vector (RLV) to compensate for the phase mismatching ?ky, thus we can achieve the QPM condition?km=?ky-Gm=0,whereGm=m(2π/Λ)is them-th-order RLV provided by the PPLN crystal,Λis the period length.The length of the positive and negative poling domains is both half of the poling period for the PPLN crystal, and the duty cycleDis 50%.In this case,we callχm(χm=2χ(2)/π=4d33/π)the effective second-order nonlinear polarization coefficient for first-order QPM.[16]Subsequently, the nonlinear coupledwave equations(11)and(12)can be rewritten as
Under the small signal approximation theory, the pump FW light is not depleted during the whole coupling process,and its intensity obeys?E10/?y=0 such thatE10=constant.Additionally,the initial boundary conditions between FW and SHW areE10(y)=E10(0),E20(0)=0, where the 0 oryin the bracket represent the chosen position in theydirection of PPLN crystal.Eventually,via solving Eq.(16),we can obtain the analytical expression of amplitude of SHW as
whereE00represents the initial electric field amplitude of the incident pump wave.By means of calculating the average Poynting vector, we can get the relations between the field amplitude and field energy of incident wave,the transmission FW and the generated SHW in crystal.Then, we can derive the conversion efficiency of SHW in the form of
whereI00is the initial intensity of the incident pump wave.In comparison to the case of small signal approximation, there is a consumption of FW energy under the general large signal theory.This means that the amplitude of the pump wave is a variant, varying with the propagation distance, and thus?E10/?y ?=0.Combining the initial boundary conditions ofE10(0)=E00?=0 andE20(0)=0, we further solve both the nonlinear coupled-wave equations(15)and(16)to find rigorous solutions.Notice that, the 0 oryin the bracket represent the chosen position in theydirection of PPLN crystal.The analytical expressions of field amplitude for FW and SHW can be derived as
Ultimately,the conversion efficiencies of FW and SHW at different incident angles when reflection and transmission are considered,can be explicitly calculated as
It can be clearly seen that the conversion efficiencies of FW and SHW are closely related to the transmission coefficientt(as seen in Eq.(3)).Besides,the crystal length,the nonlinear polarization tensor,the wavelength of incident light as well as the field amplitude of pump wave are several key factors that determine the conversion efficiencies of FW and SHW.
Up to now, the nonlinear coupled-wave equations have been established for the pump light incident upon the crystal at different angles and fully considering the reflection and transmission of the interface,and the corresponding SHG conversion efficiencies of a PPLN crystal have been delicately solved under the large and small signal theories.All the details of electromagnetic wave transport properties and nonlinear conversion can be demonstrated and solved.Based on the analytical solution,we can evaluate not only qualitatively but also quantitatively the transmission behavior and tunable characteristics of the SHG process in a PPLN crystal at the QPM interaction under the oblique-incidence pump configuration of laser architecture.
3.Simulation results
3.1.Reflection and transmission of interface
In order to visualize the effect of reflection and transmission at the LN and PPLN crystal interface,we assume that the specific wavelength of incident pump light is 1064 nm, and calculate the corresponding refractive index of FW by Sellmeier formula.[40]Here,the influence of incident angle on reflection and transmission(r,t,R,T)is explored according to Eqs.(3)and(4),and the results are clearly illustrated in Fig.2.
It can be seen from Fig.2(a) that the reflection coefficient of the incident light increases with the incident angle from 0?to 90?while the transmission coefficient decreases with the increasing incident angle.As adequately described in Fig.2(b), when the angle of incidence gets larger, the reflectivity of light energy also increases but the transmittance falls down monotonously.These phenomena are consistent with the rule that the more light is reflected, the less light is transmitted,andvice versa.Fig.2.(a)Field and(b)energy reflection and transmission for FW plane wave laser beam incident from air to LN and PPLN crystal at various oblique anglesα.
3.2.Walk-off effect of FW and SHW
In accordance with Eq.(14),the walk-off length ?xis intrinsically controlled by the incident angle and incident wavelength, besides the crystal length.At a fixed incident pump wavelength of 1064 nm, together with the length of LN and PPLN crystal isy=10 mm, the tendency of walk-off length?xin dependence on the incident angleαis calculated and plotted in Fig.3(a).Further,we investigate the trend of walkoff length ?xwith respect to incident wavelength at a fixed incident angle of 30?for a 10-mm-length LN and PPLN crystal in Fig.3(b).

Fig.3.The walk-off length of FW and SHW beams as a function of(a)incident angle at the wavelength of 1064 nm and (b) pump wavelength at the incident angle of 30?in LN and PPLN crystals.
As can be seen from Fig.3(a), the larger incident angle makes the FW and SHW transmit in two different routes separately, which easily causes the walk-off in thexdirection.Moreover, as the incident wavelength turns longer, the walkoff length will get shorter for a specific incident angle.It can be concluded that, a suitable incident wavelength or incident angle can suppress the walk-off effect to some extent.For efficient nonlinear coupling, we prefer to get a slight walk-off effect by choosing a smaller incident angle or a longer incident wavelength.
3.3.Matched wavelength of incident pump laser
In accordance with phase mismatching formula,as shown in Eq.(13),it can be accurately calculated that the phase mismatching is|?ky|=0.901 μm-1, in the situation where the incident pump light wavelength is 1064 nm and the incident angle is 0?.Them-th-order RLVGmof the single specific PPLN sample used in our numerical simulations is represented asGm=m(2π/Λ)=?ky,which compensates for the value of phase mismatching via QPM technique.For such a fixed phase mismatching ?kyfor an identified PPLN sample,we can investigate the phase matching wavelength of incident pump lightλ1varying with the incident angleα, and the result is displayed in Fig.4.
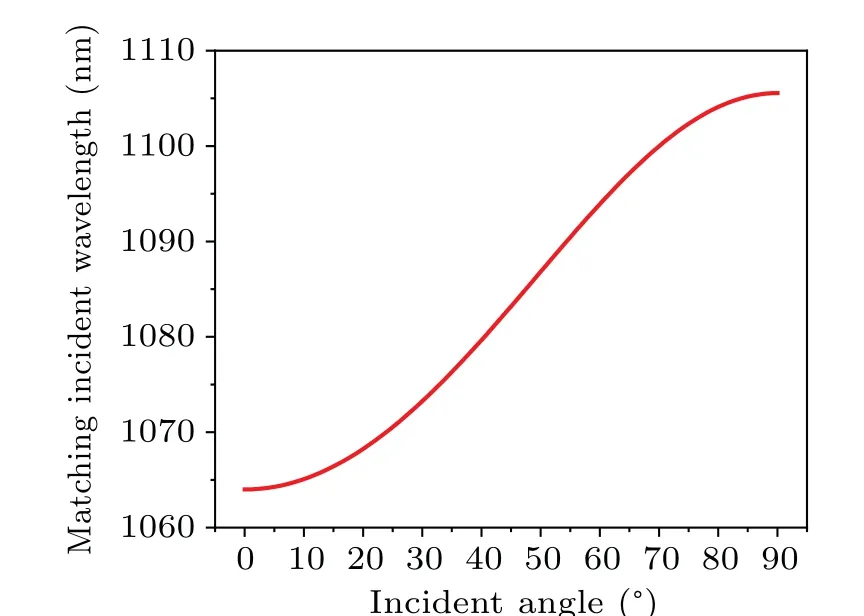
Fig.4.The phase matching wavelength of pump light as a function of incident angle for phase mismatching|?ky|=0.901μm-1 at the wavelength of 1064 nm between transmission FW and generated SHW in crystal.
Note that there is a specific matching incident wavelength at a specific angle of incidence, which corresponds one by one.Further analysis, we can find that the phase matching wavelength of pump light increases monotonically when the incident angle becomes larger.What needs illustration is that in most experimental cases, the Brewster angle is the first choice,which is mainly to minimize the reflected light energy and maximize the transmitted light energy, so as to improve the conversion efficiency of related experiments.However,in our model,we are mainly concerned with the extent to which a tunable spectrum bandwidth range can be achieved by introducing the 0?to 90?of incident angle engineering, which shows a trend of monotonic increasing.Besides, the conversion efficiency of the SHW gradually decreases with the increasing incident angle.That is to say,a compromise between the high conversion efficiency and tunable narrow-band bandwidths is fully taken into account in our scheme, rather than preferring the angle of least reflection.Under this scheme, if the range of incident angles can be idealized from 0?to 90?the phase matching wavelength of the FW can tune in the range of 1064 nm–1105.6 nm, with a rather large bandwidth of about 41.6 nm,which obviously is much larger than in the usual way of temperature or period fine tuning.According to our theoretical calculations,when the temperature of the PPLN crystal rises from 20?C–200?C by temperature tuning and the pump light stays at 0?incident on the crystal,the FW tuning range is 1063.66 nm to 1081.03 nm with a tuning range of 17.37 nm.The tuning range of this method is more limited than the angle tuning method proposed in our study.In addition, there are several problems with temperature tuning, including the requirement for high-precision temperature control equipment,the effect of temperature drift on wavelength stability,and the long response time of high-low temperature switching,and the crystal life is easy to degrade at high temperature.Indeed, it has been reported earlier that the output wavelength can be tunable by designing a single PPLN crystal with a fan structure, or by cascading multiple crystals to form different periodic structures,but with a complicated experimental setup and low conversion efficiency.In contrast,our method provides a new degree of freedom for efficient and tunable narrow-band second harmonic generation by introducing single incident angle modulation in PPLN crystals.In other words, one can simply adjust and match the incident angle corresponding to a given incident wavelength for the output the different wavelengths of SHW,and this would effectively break the limitation that a single PPLN crystal can only achieve a specific wavelength matching.Thus, it is possible to realize the nonlinear process of generating tunable narrow-band wavelength output for a single PPLN crystal based on angle-engineering.
3.4.RLVs distributions and dispersion curves
As has been pointed out,a single PPLN crystal can match different wavelengths of incident FW by choosing the corresponding appropriate incident angle.Here, the sample we use is az-cut PPLN crystal with the dimensions of 5 mm(x)×10 mm (y)×1 mm (z).The poling period of the PPLN crystalΛ=6.974 μm is given byΛ=6.974 μm (m=-1),and the duty ratio is 1:1.Distribution of RLVs and the phase mismatching dispersion curves at incident angle 0?,20?,40?,and 60?in PPLN crystal with QPM structure are calculated and plotted in Fig.5.
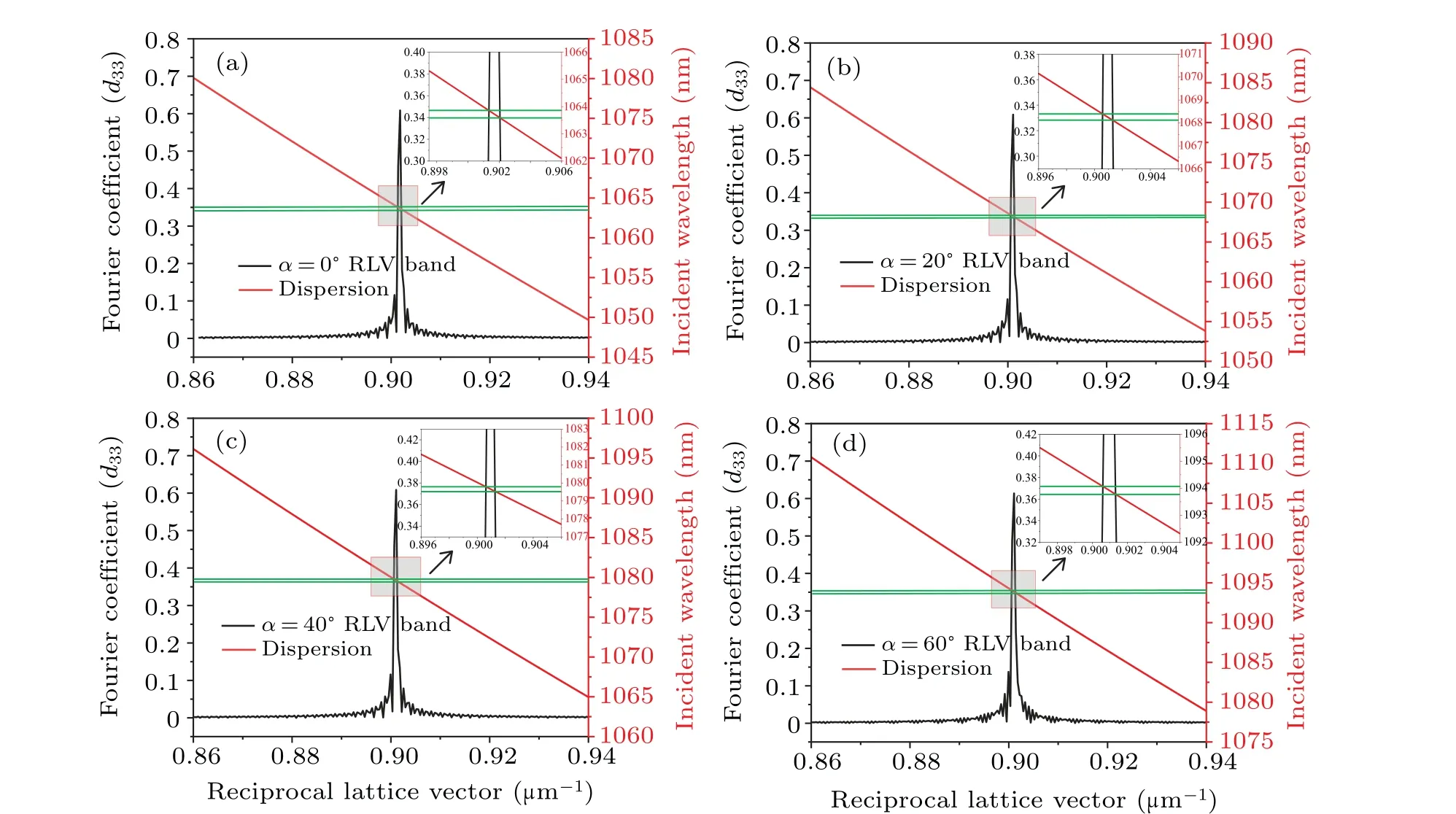
Fig.5.Distribution of RLVs and the phase mismatching dispersion curves at incident angle(a)0?,(b)20?,(c)40?,and(d)60?,respectively in PPLN crystal with first order QPM structure.
As shown in Fig.5(a),when the incident angle isα=0?,the RLV provided by PPLN crystal presents a sharp peak,and the peak value is with high Fourier coefficient of (2/π)d33.What is more, the phase mismatching dispersion curve intersects the RLV peak right at 0.901 μm-1, which exactly matches the central wavelength of 1064 nm.It means that the designed PPLN crystal can compensates the specific phase mismatching|?ky| = 0.901 μm-1between FW and SHW when SHG occurs at the incident wavelength of 1064 nm.For easy comparison, when the incident angles are 20?, 40?, and 60?, respectively, and the results are depicted in Figs.5(b)–5(d).Evidently,for a specific PPLN crystal,the incident wavelength for phase matching will change when the pump light is incident at different angles, so as to achieve QPM.In more detail,the intersection of the RLV and the phase mismatching dispersion curve occurs at the pump wavelengths of 1064 nm,1068.3 nm, 1079.7 nm, and 1093.9 nm at incident angles of 0?, 20?, 40?, and 60?, respectively.Meanwhile, the peak of the RLVs remains at|?ky|=0.901 μm-1, and the matching wavelength of pump light turns longer when the incident angle is larger.One thing worth noting is that, the actual incident angle cannot be set to 90?because the PPLN crystal does not have a corresponding domain structure alongxdirection.Therefore, when the incident angle changes from 0?to 90?the PPLN crystal with first order QPM design is appropriate for phase-mismatching compensation at incident wavelength 1064 nm–1105.6 nm, which corresponds to the output SHW of 532 nm–552.8 nm, with a considerable tunable bandwidth of 20.8 nm.This marks the realization of narrow-band tunability for the SHW in an angle-engineered PPLN crystal by means of regulating the incident angle in match with the pump wavelength.
3.5.SHW conversion efficiency
Finally,we fully consider the reflection and transmission at the crystal surface and discuss how the incident wavelength modulates the SHW conversion efficiency under general large signal theory.Similarly, we continue to analyze the incident angle of 0?,20?,40?,and 60?.The amplitude of the incident wave isE00=6×106V/m,which has great influence on the conversion efficiency.At the same time, the results in Fig.6,based on our model, also depend on the various parameters given by the analytic Eqs.(21) and (22) we derived, including the electric field amplitude,the crystal length,the incident angle, etc.Under the reflection and transmission model, the conversion efficiency of SHW is a function of phase matching wavelength of pump light at different incident angles, as displayed in Fig.6.This is based on the lattice inverse vector obtained from the Fourier transform of the crystal domain structure in Fig.5 to further calculate the conversion efficiency in the corresponding matching wavelength range, which is a reasonable explanation for why our final numerical simulation result is not a symmetric Gaussian distribution.
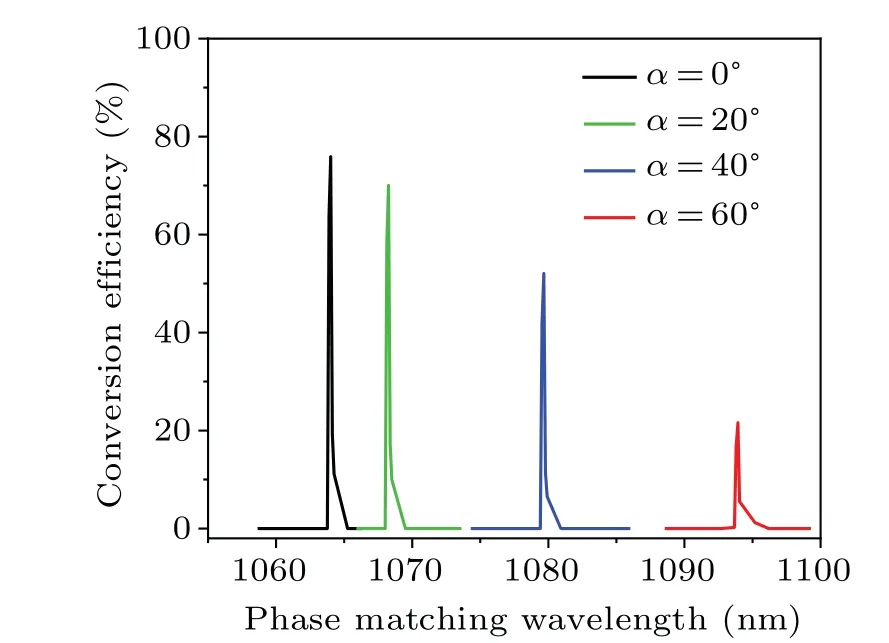
Fig.6.The conversion efficiency of SHW as a function of phase matching wavelength of the FW when the incident angles is 0?(black line),20?(green line),40?(blue line),60?(red line),respectively.
From Fig.6, SHG efficiency decreases obviously as the incident angle gets larger at a certain incident wavelength.When the pump light is incident at angles 0?, 20?, 40?,and 60?the incident wavelengths of 1064.0 nm, 1068.3 nm,1079.7 nm,and 1093.9 nm can be chosen to reach a maximum SHG efficiency about 75.9%, 70.1%, 52.1%, and 21.6%, respectively.These results can be explained from two aspects.Firstly, as the incident angle increases, the amplitude of the electric field(E10)entering the PPLN crystal will gradually decrease under the consideration of interface transmission.Forα=0?,the field amplitude of FW transmitted into the crystal is 3.81×106V/m, and it drops sharply to 1×106V/m when the incident angleαincreases to 80?.On the other hand,with the increased incident angle, the interaction length of FW in the crystal becomes significantly shorter, which reduces the conversion efficiency of SHW to some extent.Under the condition that other conditions remain unchanged, we also can try to increase the anti-reflection film plating at the outlet end to increase the light output energy, so as to further improve the conversion efficiency at a large angle.It demonstrates that for a certain incident angle, we can find a specific incident wavelength to get a maximum SHG efficiency, i.e., the optimum phase matching incident wavelength or optimum phase matching incident angle.Thus,we can ideally extend the incident angles from 0?to 90?and get narrow-band tunability of the incident wavelengths from 1064 nm to 1105.6 nm in the particular PPLN crystal through QPM schemes, resulting in narrow-band tunable SHW output.
4.Conclusions
In summary, we have proposed an angle-engineering QPM scheme and shown that the incident angle of pump laser light can be harnessed as an alternative versatile tool to engineer QPM for high-efficiency SHG in a PPLN crystal, in addition to conventional means of period adjusting or temperature tuning.We have provided a nonlinear optical theoretical system to investigate nonlinear SHG process in PPLN crystal under different incident angles of pump light.First, we have established the formalism of nonlinear coupled wave equations for SHG suitable for oblique incidence, fully considering the reflection and transmission of FW pump light at aircrystal surface.Second, under both the small signal approximation model and the general large signal model, we have rigorously solved the coupled-wave equations and derived the explicit analytical expressions of SHW field intensity and the SHG conversion efficiency for both artificial LN crystal and PPLN crystal.For a PPLN crystal, a well-established effective nonlinear coefficient model has been adopted.Finally,we have systematically analyzed the walk-off effect and the phase mismatching of FW and SHW in dependence on incident angle or pump wavelength within LN crystal and PPLN crystal.
We have performed systematic numerical simulations for a PPLN crystal with first order QPM structure to confirm our theoretical predictions for several interesting phenomena based on the exact analytical solution of the general largesignal theory.We have determined the one-to-one correspondence between the pump incident light wavelengths and the phase matching incident angle of pump light.The results show that the narrow-band tunable SHG output covers a range of 532 nm–552.8 nm at the ideal incident angles from 0?to 90?.Yet, this bandwidth has already been much larger than in the usual way of temperature or period phase matching tuning,which is on the order of 1 nm.Besides, the conversion efficiency of the SHW gradually decreases with the increasing incident angle, and this might be improved by anti-reflection coating on the LN crystal surface.
The proposed angle-engineering scheme has offered an alternative route to realize tunable QPM with a considerable broad bandwidth for high-efficiency SHG against pump laser for a pre-designated PPLN crystal,and this scheme has a superior performance compared with conventional means of period adjusting or temperature tuning in terms of tunability bandwidth.Moreover,the developed analytical theory and formalism,which fully consider the reflection and transmission at the air-crystal interface,would offer an efficient theoretical system to evaluate quantitatively the nonlinear frequency conversion processes and help to obtain the maximum SHG conversion efficiency by selecting an optimum incident wavelength and incident angle in a specially designed PPLN crystal.The angleengineering QPM scheme and associate analytical formalisms can be readily extended to handle other nonlinear optical processes such as SFG and DFG.Together they would be very helpful for the design of tunable narrow-band pulse nanosecond,picosecond,and femtosecond laser devices via PPLN and other microstructured LN crystals.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.11974119), the Science and Technology Project of Guangdong Province, China(Grant No.2020B010190001), the Guangdong Innovative and Entrepreneurial Research Team Program (Grant No.2016ZT06C594), the National Key Research and Development Program of China (Grant Nos.2018YFA, 0306200,and 2019YFB2203500),and the Science and Technology Program of Guangzhou City(Grant No.2023A04J1309).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

