一道數(shù)學奧林匹克選拔題的探究與推廣
2024-01-19 13:00:34鄭劍暉
中學數(shù)學研究(江西) 2024年2期
鄭劍暉
福建省莆田第五中學 (351100)

本題內(nèi)涵豐富,由之可得到一些有用的結(jié)論,并進一步變換出一系列數(shù)學競賽試題和數(shù)學問題.

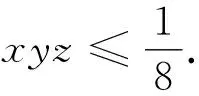
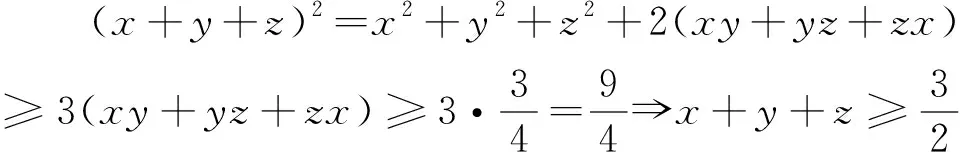
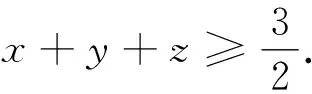
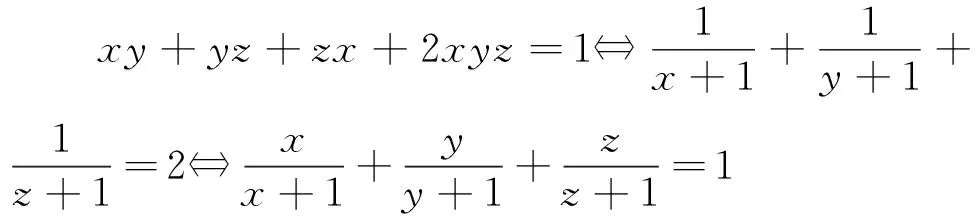
結(jié)論3 設x,y,z是正實數(shù),且xy+yz+zx+2xyz=1,則x+y+z≥2(xy+yz+zx).
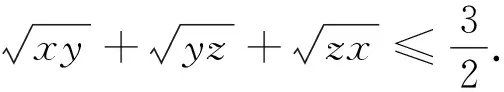
由以上結(jié)論還可以變換出一系列數(shù)學問題.
題1 (2014年羅馬尼亞數(shù)學競賽試題)已知x,y,z>0,且xyz+xy+yz+zx=4,求證:x+y+z≥3.

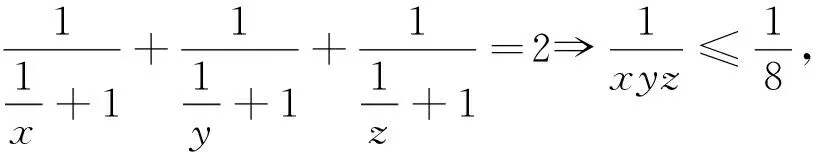
這就分別得到并證明了如下試題:

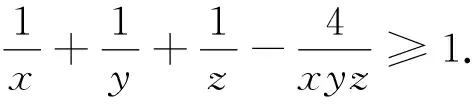
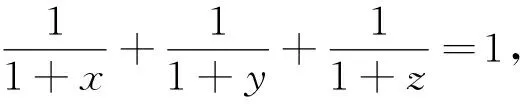
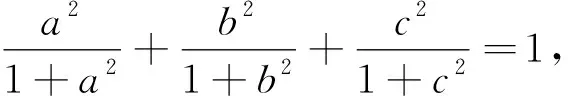
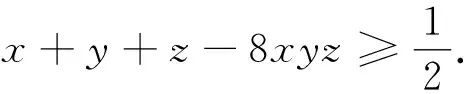
題7 (2004年地中海地區(qū)數(shù)學奧林匹克試題)已知x,y,z是正數(shù),且xy+yz+zx+2xyz=1,證明:2(x+y+z)+1≥32xyz.
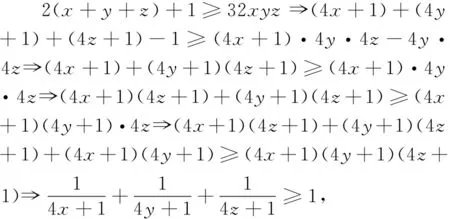
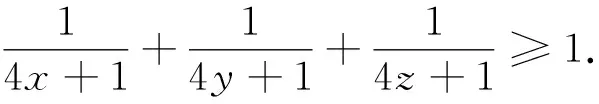
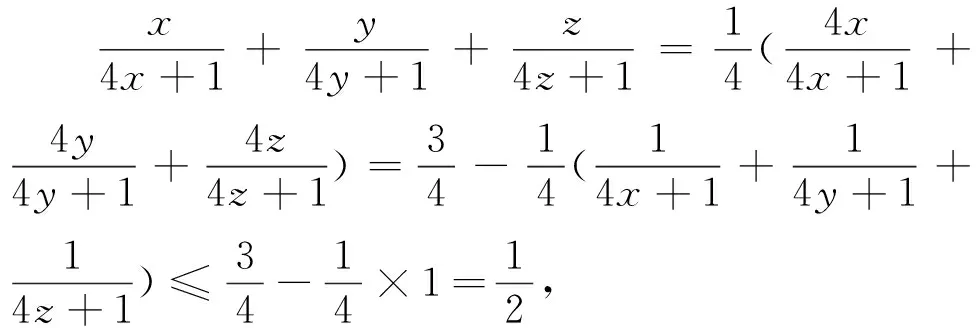
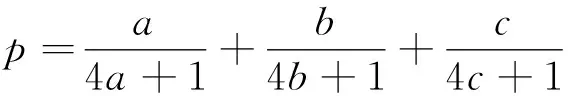
題10 (2005年哈薩克斯坦數(shù)學奧林匹克試題)已知a,b,c>0,且abc=a+b+c+2,求證ab+bc+ca≥2(a+b+c).
題11 (1996年越南數(shù)學奧林匹克試題)設x,y,z∈R+,且xy+yz+zx+xyz=4,證明:x+y+z≥xy+yz+zx.
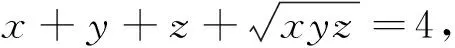
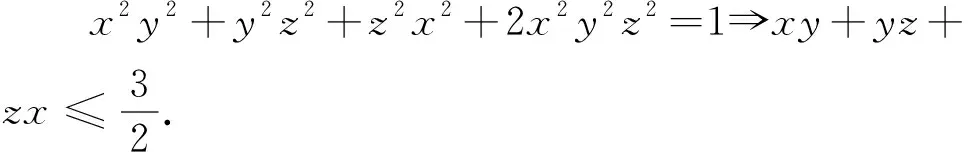
猜你喜歡
海峽姐妹(2020年4期)2020-05-30 13:00:18
中學生數(shù)理化·七年級數(shù)學人教版(2019年9期)2019-11-25 07:34:34
海峽姐妹(2019年4期)2019-06-18 10:39:12
海峽姐妹(2017年3期)2017-04-16 03:06:37
小雪花·成長指南(2016年1期)2017-02-13 10:29:30
中學生數(shù)理化·七年級數(shù)學人教版(2016年9期)2016-12-07 08:28:52
中學生數(shù)理化·七年級數(shù)學人教版(2016年8期)2016-12-07 07:25:19
中國衛(wèi)生(2016年11期)2016-11-12 13:29:24
小雪花·成長指南(2016年3期)2016-04-20 06:24:08
小雪花·成長指南(2016年2期)2016-03-16 06:38:56

