Multiplicative eccentricity resistance-distance of unicyclic graphs with a given parameter
Hong Yunchao, Miao Lianying
(School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China)
Abstract:The multiplicative eccentricity resistance-distance ξ?R(G) of a graph G is the sum of the product the corresponding eccentricity of vertices and the resistance-distance between the pairs of vertices of all unordered pairs of vertices on the graph. In this paper, we use the transformation method to characterize the extremal graphs having the maximum, the second maximum, the minimum and the second minimum multiplicative eccentricity resistance-distance among n-vertex unicyclic graphs, respectively. Moreover,we characterize the extremal graphs having the maximum, the second maximum and the third maximum multiplicative eccentricity resistance-distance among n-vertex unicyclic graphs with given maximum degree ?, respectively.
Keywords: resistance-distance, unicyclic graph,multiplicative eccentricity resistance-distance
1 Introduction
Throughout this paper, all considered graphs are simple and connected. LetG=(VG,EG) be a graph with vertex setVGand edge setEG.dG(x) is the degree of vertexxinG. The distancedG(x,y)between two verticesxandyofGis defined as the length of a shortest (x,y)-path inG. The eccentricityεG(x) (for simplicity,ε(x)) of a vertexxis the distance betweenxand a furthest vertex fromx. LetPn,CnandSnbe the path, the cycle and the star onnvertices, respectively. IfE0?E(G), we denote byG-E0the subgraph ofGobtained by deleting the edges inE0. IfE1is the subset of the edge set of the complement ofG,G+E1denotes the graph obtained fromGby adding the edges inE1. Similarly, ifW?V(G), we denote byG-Wthe subgraph ofGobtained by deleting the vertices ofWand the edges incident with them. For simplicity, we writeG-xy,G+xyandG-xinstead ofG-{xy},G+{xy} andG-{x}.
In[1],Klein D J and Randi? Mintroduced a new distance function named resistancedistance in 1993,which is defined to be the effective resistanceRG(x,y)between verticesxandyinG. This distance has proven to have a number of interpretations and applications over a widely variety of fields[2-5]. There is a family of resistive descriptorsF(G) studied in mathematical chemistry, with the general formula
whereRG(x,y)is the effective resistance between verticesxandyandfG(x,y)is some real function of the vertices.
IffG(x,y)≡1, it is the well-known KirchhoffindexKf(G), proposed by Klein D J and Randi? M in [1].Kf(G) was defined by the sum of the resistance-distances of all pairs of vertices of a graphG.Kfv(G) was defined by the sum of the resistancedistance of vertexvto the other vertices in the graphG. This index has very nice purely mathematical and physical interpretations (for example, see [6]), and has been investigated extensively in mathematical, physical and chemical literatures, for more detail information the readers are referred to recent papers[7-10] and references therein.In [11], Chen Haiyan and Zhang Fuji introduced naturally an indexR?(G) named multiplicative degree-Kirchhoffindex from the relations between resistance-distance and the nomalized Laplacian spectrum. It is defined exactly by equation(1) when takingfG(x,y) =dG(x) ·dG(y). Comparing with this index, Gutman Ivan, Feng Linhua and Yu Guihai[12]proposed the additive degree-KirchhoffindexR+(G) which can also be obtained by lettingfG(x,y)=dG(x)+dG(y)in equation(1). Some interested properties and relations among these three Kirchhoffian indices are obtained,see[13-17]and references therein.
Motivated by these works above,Li Shuchao and Wei Wei[18]defined the eccentricity resistance-distance sumξR(G) from equation(1) by takingfG(x,y) =ε(x)+ε(y).Some mathematical properties and extremal problems onξR(G) are considered. Further,Hong Yunchao et. al.[19]defined the multiplicative eccentricity resistance-distanceξ?R(G) from equation(1) by taking
whereε(·) is the eccentricity of the corresponding vertex andRG(x,y) is the effective resistance between verticesxandy. Some mathematical properties and extremal problems onξ?R(G) are considered, see [20-21].
In this paper, we concentrate still on unicyclic graphs. A graphGis called a unicyclic graph if it contains exactly one cycle. LetG=U(Ck;T1,T2,··· ,Tk) be the unicyclic graph withCk=v1v2···vkv1as the unique cycle inG, and for eachi(1 ≤i≤k), letTibe the component ofG-(V(Ck)-vi). Obviously,Tiis a tree.Denote |G| = |VG| for a graphG, then anyn-vertex unicyclic graphGwith a cycle onkvertices is of the formU(Ck;T1,T2,··· ,Tk), whereIn particular, ifTi=P|Ti|andviis one terminal vertex ofP|Ti|,then we denoteTiasP|Ti|for 1 ≤i≤k.Obviously, ifTiis trivial, thenTi=P1for 1 ≤i≤k.
For convenience, letU(n,k) be the set of all unicyclic graphs onnvertices containing cycleCk,Skndenote the graph obtained from cycleCkby addingn-kpendant edges to one vertex ofCk,Pkndenote the graph obtained by identifying one end-vertex ofPn-k+1with any vertex ofCk,U(n)be the unicyclic graph withnvertices. LetPl-1be the path with the verticesv1,v2,··· ,vl-1, the graphT(l,i,1) be constructed fromPl-1by adding one pendant edge to the vertexvi(2 ≤i≤l-2), the unicyclic graphU(Ck;T(l,i,1))(k≥3,2 ≤i≤l-2,l+k=n+1) be the graph obtained from cycleCkby joiningv1ofT(l,i,1) to a vertex ofCk.
We study some mathematical properties ofξ?R(G). As their applications, the extremal graphs with the maximum, the second maximum, the minimum and the second minimum multiplicative eccentricity resistance-distance among unicyclic graphs are characterized, respectively. Moreover, we characterize the extremal graphs of the maximum, the second maximum and the third maximum multiplicative eccentricity resistance-distance ofn-vertex unicyclic graphs with given maximum degree ?, respectively.
The following lemma that will be used in the proof of our main results.
Lemma 1.1[1]Letxbe a cut vertex ofGandu,vbe vertices belonging to different components ofG-x. ThenRG(u,v)=RG(u,x)+RG(x,v).
Lemma 1.2[1]LetCkbe a cycle with lengthkandv∈Ck. Then
Lemma 1.3[22]LetGbe a connected graph with a cut-vertexvsuch thatG1andG2are two connected subgraphs ofGhavingvas the only common vertex andV(G1)∪V(G2)=V(G). Letn1=|V(G1)|-1,n2=|V(G2)|-1. Then
2 Some transformations and proofs
In this section, we introduce some transformations which will increase or decreaseξ?R(G). For convenience, in the following of our context, for any two verticesx,yofG(resp.G′,G′′), letε(x) =εG(x) (resp.ε′(x) =εG′(x),ε′′(x) =εG′′(x)) andRxy=RG(x,y) (resp.R′xy=RG′(x,y),R′′xy=RG′′(x,y)).
Lemma 2.1[20]Given a connected graphGwith a cut vertexuanddG(u)≥3.LetPk+1=uu1u2···ukandPt+1=uv1v2···vt(k≥t)be two pendant paths attaching atu, and setG′=G-vt-1vt+ukvt, thenξ?R(G′)>ξ?R(G).
Given three disjoint connected graphsG1,G2and a pathP=vv1···vt-1vt, letu1∈VG1,u2∈VG2. Suppose thatHis the graph obtained fromG1andG2by identifyingu1andu2tou. We call this procedure an identification operation[22],which denoted by the formula (H,u) = (G1,u1)⊕(G2,u2). LetGbe a connected graph constructed by identifyingvinPanduinH, that is (G,u) = (H,u)⊕(P,v).LetG′be the graphs formed by the identification operation as follows:
The graphsGandG′are depicted in Fig. 1.
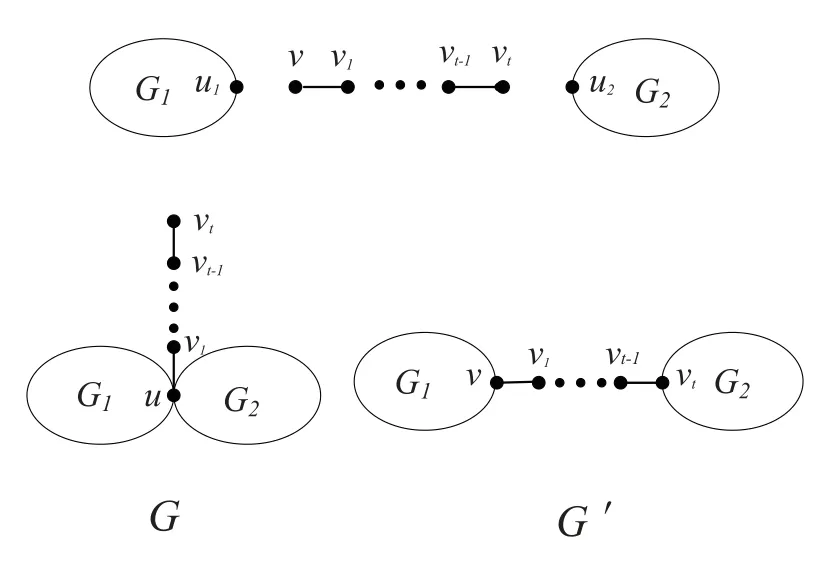
Fig. 1 Graphs G and G′ in Lemma 2.2
Lemma 2.2[20]LetGandG′be the graphs defined above. Thenξ?R(G′)>ξ?R(G).
Lemma 2.3[20]Letuandvbe two vertices inG1such that the distance betweenuandvis the diameter ofG. LetG,G′andG′′be the graphs formed by the identification operation as follows:
Then
(i) IfKfv(G1)≥Kfw(G1),ξ?R(G′)>ξ?R(G);
(ii) IfKfu(G1)≥Kfw(G1),ξ?R(G′′)>ξ?R(G).
Lemma 2.4[20]LetCk(k≥4) be an end cycle inG, anduk-3,uk-2,uk-1be three successive vertices lying inCk,as shown in Fig. 2. LetG′=G-uuk-1+uk-3uk-1,thenξ?R(G′)>ξ?R(G).
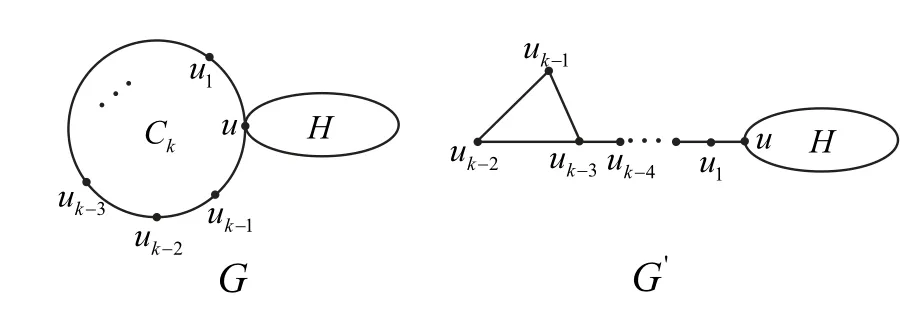
Fig. 2 Graphs G and G′
Lemma 2.5[19]LetHbe a connected graph andK1,p+1be a star with centerv.LetGbe the graph obtained fromHandK1,p+1by identifying a vertex ofH, sayu,with a pendant vertex of the star. LetG′be the graph obtained fromGby moving all the pendant edges fromvtou. Thenξ?R(G)≥ξ?R(G′), the equality holds if and only ifHis a trivial graph.
Lemma 2.6[19]Letu(resp.v) be a vertex ofGsuch that there arep(resp.q)pendant verticesu1,u2,...,up(resp.v1,v2,...,vq) attached atu(resp.v). Let
Then eitherξ?R(G)>ξ?R(G′) orξ?R(G)>ξ?R(G′′).
LetCkbe a cycle withk-vertices(k≥3),Tibe a tree withi-vertices(i≥2) andT1,tbe a star with a center vertexv′. Letu,v∈Ckands∈Ti. LetG′andG′′be the graphs formed by the identification operation as follows:
The graphsG′andG′′as shown in Fig. 3.
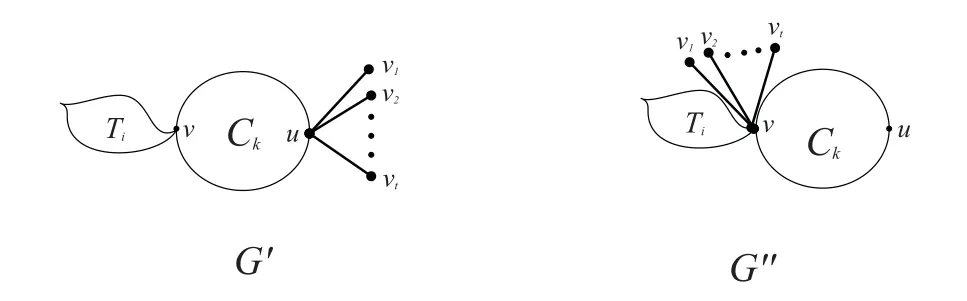
Fig. 3 The graphs G′ and G′′ in Lemma 2.7
Lemma 2.7LetG,G′,G′′be the graphs defined above, thenξ?R(G′)>ξ?R(G′′).
ProofLetH=VTi{v} andW={v1,v2,··· ,vt}. Note that
Hence, one hasVG′=VG′′=VG∪W, and
This gives
Therefore, it is easy to see that
Further, we have
Letx0be a vertex with the minimum eccentricity inVCkofG′′, that is, there isε′′(x0) =min{ε′′(x),x∈VCk}. Note thatξ?R(G′) -ξ?R(G′′) =ξ1+ξ2andv1∈W.Then we have
Hence,ξ?R(G′)>ξ?R(G′′).
Lemma 2.8Among all graphs inU(n,k)(n≥5,k≥4),thenξ?R(Skn)>ξ?R(Sk-1n).
ProofLetG=Skn,G′=Sk-1nand (G,u) = (Ck,u)⊕(Sn-k+1,u), (G′,u) =(Ck-1,u)⊕(Sn-k+2,u). LetH=G-(Sn-k+1-u),H′=G′-(Sn-k+1-u). According to the construction ofSknand, it is easy to see thatε(x)≥ε′(x) for anyx∈VG.
By Lemmas 1.2 and 1.3, we have
Hence by a direct calculation, we have
Therefore, it is easy to see thatξ?R(G)-ξ?R(G′)>0 fork≥8.
Now we consider 4 ≤k≤7. Here we only showξ?R(G) >ξ?R(G′) fork= 4.Similarly,ξ?R(G)>ξ?R(G′) holds fork=5,6,7.
Whenk=4,G′=S3n,G=S4n, we have
So whenk=4,ξ?R(G)>ξ?R(G′).
To sum up, we haveξ?R(Skn)>ξ?R(Sk-1n)(n≥5,k≥4).
3 Main results
In this section, we will determine the elements inU(n,k) with the maximum, the second maximum, the minimum and the second minimum multiplicative eccentricity resistance-distance by the transformations which we have obtained.
3.1 Extremal unicyclic graph with the maximum and the second maximum ξ?R(G)-value
Theorem 3.1LetG∈U(n,k) withn≥5, thenξ?R(G)≤ξ?R(P3n).
ProofLetG=U(Ck;T1,T2,··· ,Tk) be a any unicyclic graph. By repeating Lemma 2.5,we transform all the pendant tree of each vertex on the cycle of the unicyclic graph into a pendant path, so get
Take the largest diameter on the cycle of the unicyclic graph, determine its two endpoints,and by repeating Lemma 2.3 to transform the pendant path of other vertices on the cycle to the endpoints, respectively. By repeating Lemma 2.1, we transform all pendant paths at each endpoint into one path; By Lemma 2.2, connect one of the remaining two pendant path to the vertex of degree 1 of the other one. In each of these transformations, the multiplicative eccentricity resistance-distance is increasing,hence we haveξ?R(U(Ck;P|T1|,P|T2|,··· ,P|Tk|)) ≤ξ?R(Pkn). By Lemma 2.4, we haveξ?R(Pkn)≤ξ?R(P3n).
It is easy to see that we haveξ?R(G)≤ξ?R(P3n).
Theorem 3.2LetG∈U(n,k)-P3nwithn≥5, then
ProofBy Lemmas 2.1, 2.2, 2.3, 2.4 and 2.5, the graph inU(n,k) with the second maximum multiplicative eccentricity resistance-distance must be one of a graph in {U(C3;P1,P2,Pn-3),P4n,U(C3;T(n-2,n-4,1))} (as shown in Fig. 4).
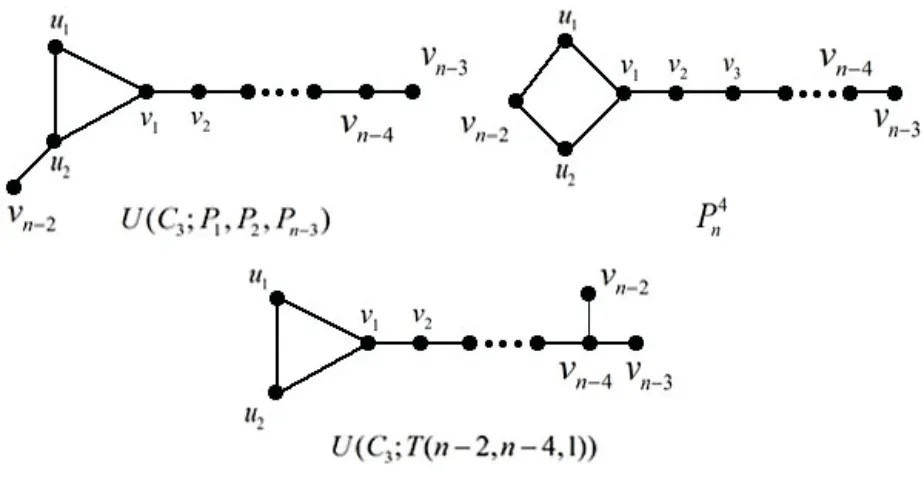
Fig. 4 The graphs U(C3;P1,P2,Pn-3),P4n and U(C3;T(n-2,n-4,1))
For the transformation fromU(C3;P1,P2,Pn-3)toP4n,it is easy to see thatε(x)=ε′(x) for anyx∈VG. Therefore, we have
LetH=U(C3;P1,P2,Pn-3)-(Pn-3-v1),H′=P4n-(Pn-3-v1). By Lemmas 1.2 and 1.3, we obtain
Hence by a direct calculation, we have
Therefore, it is easy to see thatξ?R(U(C3;P1,P2,Pn-3))-ξ?R(P4n)>0 forn≥5.
So we haveξ?R(U(C3;P1,P2,Pn-3))>ξ?R(P4n)(n≥5).
LetU(C3;P1,P2,Pn-3) =H0+u2vn-2, thenU(C3;T(n-2,n-4,1)) =H0+vn-4vn-2. It is obvious to see thatε(x)≥ε′′(x),Rxy=R′′xyfor any {x,y}?VH0andfor anyx∈VH0.
Therefore, we obtain that
Whennis even, we have
Similarly, whennis odd, we still obtain that
To sum up, we haveξ?R(G)≤ξ?R(U(C3;P1,P2,Pn-3))(n≥5).
Corollary 3.1Among all graphs inU(n,k),P3nandU(C3;P1,P2,Pn-3) are the graphs with the maximum and the second maximum multiplicative eccentricity resistance-distance, respectively.
3.2 Extremal unicyclic graph with the minimum and the second minimum ξ?R(G)-value
Theorem 3.3LetGbe a unicyclic graph of ordern(n≥5), then we have, the equality holds if and only ifG=S3n.
ProofAccording to Lemmas 2.3, 2.5, 2.6, 2.7 and 2.8, using the same method as Theorem 3.1, we have obtained the result thatξ?R(G)≥ξ?R(S3n).
By a direct calculation, we have
In what follows we determine the unique graph inU(n,k) having the second minimumξ?R(G)-value.
Theorem 3.4LetG∈U(n,k)-S3n(n≥5), thenξ?R(G) ≥9n2-36n+25, the equality holds if and only ifG=S4n.
ProofBy Lemmas 2.3, 2.5, 2.6, 2.7 and 2.8, the graph inU(n,k) with the second minimum multiplicative eccentricity resistance-distance must be one of a graph in {U?1,U?2,S4n} (as shown in Fig. 5).
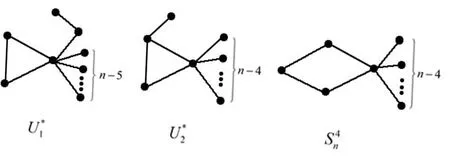
Fig. 5 The graphs U?1,U?2 and S4n
By direct calculation, we have
Sincen≥5, so we get
Thenξ?R(U?1)>ξ?R(S4n),ξ?R(U?2)>ξ?R(S4n). Hence our result holds.
Corollary 3.2Among all graphs inU(n,k)(n≥5),S3nandS4nare the graphs with the minimum and the second minimum multiplicative eccentricity resistance-distance,respectively.
Corollary 3.3Among all graphs inU(n,k)(n≥5),ξ?R(S3n) ≤ξ?R(G) ≤ξ?R(P3n)holds.
Corollary 3.4Letk0be a fixed positive integer andk0≥3, among all graphs inholds.
4 The multiplicative eccentricity resistance-distance of unicyclic graphs with given maximum degree
In this section, we determine the maximum multiplicative eccentricity resistancedistance ofn-vertex unicyclic graphs with maximum degree ?, and characterize the extremal graphs.
For convenience, we employ the following notion. LetTn,?[23]be the tree onnvertex obtained from a pathPn-?+1and empty graphby joining one end-vertex ofPn-?+1with every of. Anddenote the set of the graphs obtained fromPkt(t≤n-1) by attachingn-tpendent edges to one vertex such that its degree achieves maximum degree ?among all vertices. It is obvious thatSnn=Pnn=Cn.
LetGn,?be the set ofn-vertex graphs with maximum degree ?andU(n,k,?)be the set ofn-vertex unicyclic graphs with maximum degree ?, as we work with connected graphs only, the case ?= 1 becomes possible onlyn= 2. Similarly, for?=2 the only elements ofU(n,k,?)are the pathPnand the cycleCn. Thus,we may assume that 3 ≤?≤n-1 holds in the sequel. We start our proofs with a very simple lemma.
Lemma 4.1Assume that the vertex of maximum degree belongs toV(Tk). Then
ProofRepeating the transformation of Lemma 2.5, we have
Similarly, it is obvious to see that
And so on and so further, we get the conclusion that
Then the result follows.
Lemma 4.2LetG∈U(n,k,?),G?and assume that the vertex of maximum degree belongs toV(Tk). Thenξ?R(G)<ξ?R(H) for anyH∈
ProofSuppose thatG0=U(Ck;T1,T2,··· ,Tk)has the maximum multiplicative resistance-distance amongU(n,k,?).
Claim 1For eachi,Tiis a path withuias one of its end vertices.
For eachi,W(Ti) is maximal if and only ifTiis a path and it is easy to observe thatWui(Ti) is maximal if and only ifTiis a path withuias one of its end vertices.Henceε(ui) andKfui(G) are going to increase. For anyG=U(Ck;T1,T2,··· ,Tk) ,we have
Therefore, Claim 1 holds.
Claim 2Ifk Suppose to the contrary that there exists at least two trees such that they all have more than one vertices. LetTiandTjbe two such trees. By Claim 1,TiandTjare both paths. Leta≠uiandb≠ujbe end vertices ofTiandTj, respectively. Without loss of generality, assume thatKfa(G0) ≥Kfb(G0). Letcbe the neighbor ofbandG′0=G0-cb+ab. Now we show thatξ?R(G′0)>ξ?R(G0). For any two verticesx,ydifferent fromb, letH=G-cb, thenG′=H+ab, we haveRxy=,ε′(x)>ε(x) for anyx,y∈VH. it is obvious to see that Let vertexx0be the vertex with the minimum eccentricity inHofG0, that is, there isε(x0)=min{ε(x):x∈VH}. Then SinceKfa(G0) ≥Kfb(G0),Rab It follows thatξ?R(G′0)>ξ?R(G0),it is contradict to the choose ofG0,which implies Claim 2. By Claims 1 and 2 yield Lemma 4.2, as desired. Lemma 4.3For anyG∈Gn,?, it holds thatξ?R(G) ≤ξ?R(Tn,?) with equality if and only ifG=Tn,?. ProofLetube the vertex with maximum degree ?, we consider the following three cases. Case 1IfGis tree, letTi(i= 1,2,··· ,?-1,?) be the component ofuandG=G(u;T1,T2,··· ,T?). By Lemma 2.5, we have Assume thatP|Tj|is the longest path, by repeating use Lemma 2.1, we have wherePmbe thej-th component path. SinceG(u;P2,··· ,P2,Pm,··· ,P2)∈Tn,?, thenξ?R(G)≤ξ?R(Tn,?)with equality if and only ifG=Tn,?. Case 2IfGis not tree, then there exists a cycle inG. Without loss of generality, assume that the vertex with maximum degree ?not in the cycle. By similar arguments as above, according to Lemmas 2.1, 2.4 and 2.5, we can easily getξ?R(G)≤ξ?R(G(u;P2,··· ,P2,P(C3),··· ,P2)),whereP(C3)be thej-th component path and the cycleC3lied in the this path. Since for any the graphGofn-vertex, we haveξ?R(G) ≤ξ?R(Pn). It is obvious to see that Therefore, we getξ?R(G)≤ξ?R(Tn,?). The same is true when there exists at least two cycles inG. Case 3IfGis not tree, then there is a cycle inGand the vertex with maximum degree ?in the cycle, we can prove it in the same method, and we will not repeat the statement here. To sum up, we obtained thatξ?R(G) ≤ξ?R(Tn,?) holds, the equality if and only ifG=Tn,?. According to Lemmas 4.1 and 4.3, the number of the maximum degree less values is greater, i.e. when only need to discuss only one of the maximum degree situation can be. Theorem 4.1LetG∈and 3 ≤k≤n,thenξ?R(G)≤ξ?R(),the equality holds if and only ifG=. ProofBy Lemma 4.3,ξ?R(G)(G∈) achieves maximum only ifGis one of two special graphs in(as shown in Fig. 6). LetU′(Ck,?)(U′′(Ck,?),respectively)be this kind of graph of(a)((b),respectively)in Fig. 4. By Lemma 2.5, it is obvious to see that LetG0=U′′(C3,?)-{vwi}+{uwi}(i= 1,2,··· ,?-3), where graphs,U′′(C3,?) andG0are depicted in Fig. 7. Fig. 7 The graphs ,U′′(C3,?) and G0 By Lemma 2.6, we haveξ?R()>ξ?R(G0). LetH=U′′(C3,?)-{vwi}(i=1,2,··· ,?-4,?-3), then we haveH=G0-{uwi}(i=1,2,··· ,?-4,?-3). It is easy to see that Hence we get So we haveξ?R(G0)=ξ?R(U′′(C3,?)). We obtainξ?R(P3n,?)>ξ?R(U′′(C3,?)). Clearly,the resultξ?R(G)≤ξ?R() holds with the equality holds if and only if Theorem 4.2LetG∈U(n,k,?)-(n≥6), thenξ?R(G)≤ξ?R(). ProofBy Lemmas 4.1, 4.2 and 4.3, the graph inU(n,k,?) with the second maximum multiplicative eccentricity resistance-distance must be one of a graph in(as shown in Fig. 8). Where let the pendant edges ofubeuwi(i=1,2,··· ,?-3) in. And let Fig. 8 The graphs ,and LetH=-(C4-u). For the transformation fromto, it is easy to see thatε′(x)=ε(x) for anyx∈VG,=Rxyfor any {x,y}?VH. Hence, we have Whenn-?is odd, we have Hence we haveη5> 0. Similarly, whenn-?is even, we still obtain thatη5> 0.Therefore, we obtain thatξ?R()-ξ?R() =η4+η5> 0. It is easily check thatξ?R()>ξ?R() forn≥6. LetH?=-(u2vn-?-u),then=H?+w1vn-?. For the transformation fromto, it is easy to see thatε?(x) =ε′(x) for anyx∈VG,=for any {x,y}?VH?. Hence we get So we getξ?R()>ξ?R()(n≥6). To sum up, we haveξ?R(G)≤ξ?R()(n≥6). By Theorem 4.2, we get maxCombining with Theorem 4.1, we have the following corollary. Corollary 4.1Among all graphs inU(n,k,?)(n≥6),,andthe graphs with the maximum,the second maximum and the third maximum multiplicative eccentricity resistance-distance, respectively. Above the extremal graphs with the maximum multiplicative eccentricity resistancedistance among the unicyclic graphs with fixed number of vertices and maximum degree is characterized. In the case of minimal values,the extremal graphs are difficult to characterize, to determine the minimum multiplicative eccentricity resistance-distance is also hard, hence this study will be a very challenge work.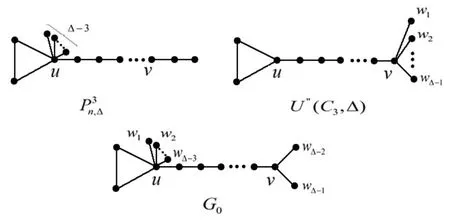

 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)2023年4期
純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)2023年4期
- 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)的其它文章
- 外推的MHSS迭代法求解一類大型稀疏的復(fù)對稱線性系統(tǒng)
- Research on multi-factor stock selection model based on random forest algorithm
- 一類離散無向圖模型誘導(dǎo)的概念類的樣本壓縮方案
- 一類高維多響應(yīng)變量誤差模型的極小極大下界
- Almost primes in generalized Piatetski-Shapiro sequences
- On primes in kth-power progressions on average
