吳婷婷, 韓 菲, 孫文靜

(新疆師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 新疆 烏魯木齊 830017)

0 引言

十八世紀(jì)產(chǎn)生了偏微分方程這門學(xué)科,一開始偏微分方程問題主要來源于物理和幾何問題,偏微分方程的研究在十九世紀(jì)得到了飛快地發(fā)展,這門學(xué)科現(xiàn)在已經(jīng)成為當(dāng)代數(shù)學(xué)中不可缺少的一部分,許多領(lǐng)域中的數(shù)學(xué)模型都可以用偏微分方程來描述.在偏微分方程課程的學(xué)習(xí)中,曲面的平均曲率是一個非常重要的概念,并且,平均曲率方程在幾何偏微分方程中也是一個基礎(chǔ)且重要的一類方程,因此,很多數(shù)學(xué)家研究其解的存在性并給出解的先驗估計.

假設(shè)Ω是Rn中的光滑有界區(qū)域,u是Ω上的光滑函數(shù).那么u的圖的平均曲率可以表示為

設(shè)u是定義在[0,1]上的光滑函數(shù),則對應(yīng)的曲線的曲率為

(1)

平均曲率方程通常具有以下兩種形式,當(dāng)描述的u(·,t)的圖是以平均曲率的大小和方向移動的曲面時,描述的方程可以表示為

當(dāng)描述的u(·,t)的圖是以平均曲率大小沿著xn+1的方向移動時,描述的方程可以表示為

對于上述兩種形式的平均曲率方程已經(jīng)被很多學(xué)者研究[1-5].

Guan[6]研究了當(dāng)n≥2時,下面的預(yù)定夾角邊界值條件的平均曲率方程

趙曉陽考慮的是下面的平均曲率流方程[7]

其中fz(x,z)≥-κ,κ>0,Ω∈Rn為有界的C3區(qū)域,n≥2,T為固定的正常數(shù),并且得到估計

接下來,研究與式(1)相關(guān)的方程

(2)

其中f(x,u,Du)是定義在Ω×R×Rn上的光滑函數(shù).

基于拋物偏微分方程解的梯度估計證明[9-10],構(gòu)造合適的輔助函數(shù),利用極大值原理推出一類拋物型方程中關(guān)于f依賴于x,u,Du時解的梯度估計的結(jié)果.

1 主要結(jié)果

(3)

(4)

u(x,0)=u0(x) ,x∈Ω

(5)

fz(x,z,p)≥-κ,κ≥0

(6)

(7)

|ψ(x)|C3(Ω)≤L2

(8)

(9)

引理1[8]假設(shè)對于固定的T>0,u∈C3(Ω)×[0,T]是方程(2)的解,并且有|u|≤M0,如果f(x,p,z)∈C1(Ω×[-M0,M0]×Rn)滿足不等式(6)和不等式(7),則對任意的子區(qū)域Ω′?Ω,可以得到

下面將給出一些定義和符號,并且對ut進行估計.

記Ω為Rn中的有界區(qū)域,n≥2,?Ω∈C3,并且記

d(x)=dist(x,?Ω),Ωμ={x∈Ω:d(x)<μ},

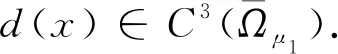
|Dν|+|D2ν|≤C(n,Ω)x∈Ωμ1

νiDjνi=0,νiDiνj=0,|ν|=1,x∈Ωμ1

(10)

定義

Cij=δij-νiνj,x∈Ωμ1,

對于向量ξ∈R2,記ξ′表示具有第i分量為Cijξj的向量.所以

(11)

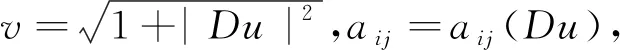
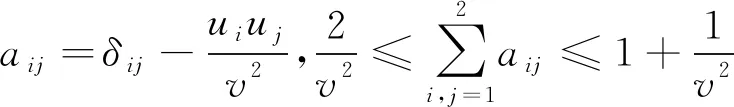
(12)

引理2 對于方程(3)-(5),假設(shè)fu≥-κ.則有估計式

先假設(shè)t0>0,則有兩種可能性

(a)x0∈?Ω.將方程(3)兩邊分別對t進行求導(dǎo),得到

(13)

而

(14)

將式(13)代入式(14)可得

(fu(x,u)+k)e-κtut-fpl(x,u,Du)e-κtult.

由于fu≥-κ,則e-κtut滿足橢圓方程的強極值原理.由邊界條件可以得到utν=ψt=0,與Hopf引理矛盾.所以情況(a)不存在.

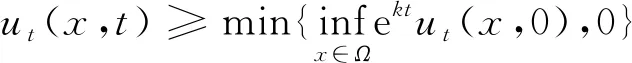
接下來證明定理1.根據(jù)Ma-Xu[4]中的方法,令w=u-ψ(x)d,選取下面的輔助函數(shù)

其中μ0是一個小于μ1的正常數(shù),α,λ是正常數(shù),并將在之后給出.

情形1x0∈?Ωμ0∩Ω.通過引理2,可以得到梯度估計.

情形2x0∈?Ω.證明方法與文[7]一致.

如果Φ(x)在(x0,t0)∈?Ω×[0,T′]處達(dá)到最大值,那么在(x0,t0),有

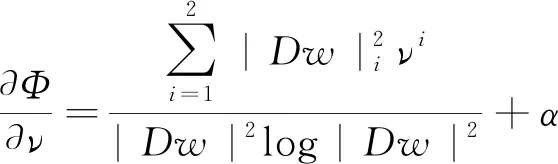
(15)

因為

wi=ui-ψxid-ψνi

(16)

在邊界?Ω上有

(17)

結(jié)合式(10),式(11)和式(17),可以得到

(18)

接下來,有

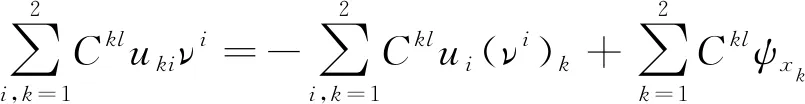
(19)

將式(19)代入到式(18)中,并結(jié)合式(4),式(15),有

(20)

根據(jù)式(16)可以在邊界上得到

|Dw|2=|Du|2-ψ2.

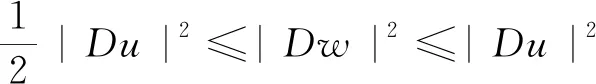
(21)

|Dw|2≥50

(22)

將式(21)和式(22)代入到式(20)中,可以得到

(α-|ψ|C0(Ω×[-M,M])-C0)|Dw|2log|Dw|2

=|Dw|2log|Dw|2>0,

其中取α=|ψ|C0(Ω×[-M,M])+C0+1,C0為只依賴于n,Ω的正常數(shù),有

和Hopf引理矛盾,那么可以得到|Du|(x0)≤C.

情形3x0∈Ωμ0.在這個假設(shè)下,x0是Φ的臨界點.在這里,使用w在x0處選擇一個特殊的坐標(biāo)系,使得

w1(x0,t0)=|Dw|(x0,t0)>0,w2(x0,t0)=0.

因為w=u-G,G=ψ(x)d,則wk=uk-Gxk,

因此,在(x0,t0)處,有

w1=u1-Gx1=u1-ψx1d-ψν1,

0=w2=u2-Gx2=u2-ψx2d-ψν2.

在(x0,t0)點,可以假設(shè)

u1≥200(|ψ|C0(Ω×[-M,M])+1) ,

否則,可以得到|Du|(x0)的界限,那么

通過前面的準(zhǔn)備,可以將|Du|(x0,t0)的估計分成3個步驟.正如之前所描述的,所有的計算都是在固定點(x0,t0)來進行的.

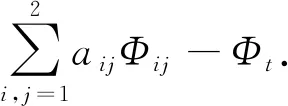
繼續(xù)對Φt求導(dǎo)數(shù)

根據(jù)方程(3)

(23)

下面將得到|Dw|2的一階和二階導(dǎo)數(shù)

(24)

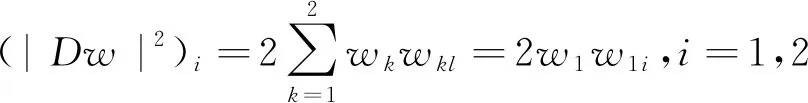
(25)

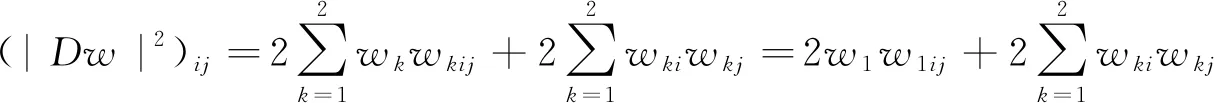
(26)

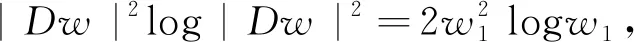
(27)

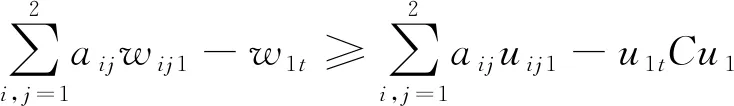
(28)

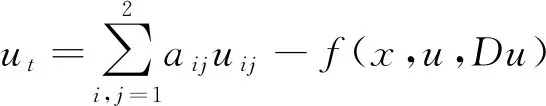
(29)

其中D1f=fx1+fuu1+fpmum1.根據(jù)式(12)可以得到

(30)

通過式(30)和式(29),可以得到

(31)

將式(31)代入到式(28),有

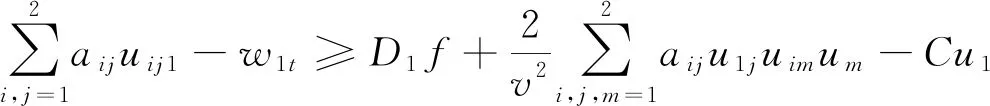
(32)

通過式(32)和式(27),得到

(33)

最后,將繼續(xù)對式(33)的每一項進行估計.然后就結(jié)束證明并得到估計式(9).

根據(jù)Φi(x0,t0)=0和式(25),可以得到對i=1,2

w1i=-αw1logw1vi

(34)

將w1i=u1i-Gx1xi代入到式(34)中,根據(jù)選擇的坐標(biāo)系,可以得到對i=1,2

u1i=-αw1logw1vi+Gx1xi

(35)

通過式(34)和式(35),可以得到

(36)

并且根據(jù)不等式(6)和不等式(7),可以得到

(37)

將式(36),式(37)代入到式(33)中,最終得到

因此得到了在x0∈Ωμ0點的界限|Du|(x0,t0).

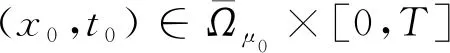
定理3的證明對于T>0,方程(7)在Ω×[0,T]上是一致拋物線方程.由定理1,引理2和ut估計,并結(jié)合偏微分方程的標(biāo)準(zhǔn)理論可以完成定理2的證明.

2 總結(jié)

研究結(jié)果主要是推廣趙曉陽的拋物方程中關(guān)于f只依賴于x,u時該方程解的C0估計和C1估計,即拋物方程中關(guān)于f依賴于x,u,Du時該方程解的C0估計和C1估計.