Absorption spectra and enhanced Kerr nonlinearity in a four-level system
Hao-Jie Huangfu(皇甫浩杰), Ying-Jie Du(杜英杰),2,?, and Ai-Hua Gao(高愛華)
1School of Physics,Northwest University,Xi’an 710069,China
2Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
Keywords: double electromagnetically induced transparency(EIT),Autler–Townes splitting,Kerr nonlinearity,four-wave mixing
1.Introduction
Third-order nonlinearities, including Kerr nonlinearity,four-wave mixing (FWM), Raman effect and so on, have attracted considerable interests in these years due to their promising applications such as optical quantum computing,quantum logic gates and nonlinear optical control.[1–9]Atoms interacting with coherent radiation fields can give rise to many interesting physical phenomena, such as electromagnetically induced transparency (EIT),[10,11]Autler–Townes(AT) splitting,[12,13]electromagnetically induced absorption(EIA),[14,15]coherent population trapping(CPT)[16,17]and so on.In the past decades, researchers have conducted extensive studies on various kinds of nonlinearities caused by destructive and constructive quantum coherence in atomic systems with different energy level structures.[18–22]For a threelevel EIT system, the Kerr nonlinearity was measured by applying an optical ring cavity and obtained a greatly enhanced Kerr nonlinearity consistent with theory.[23]However,in three-level systems, significant nonlinear susceptibilities rely on a low-intensity coupling field, which may result in a heightened loss of the probe field.Compared to threelevel systems,four-level systems have a more intricate energy level configuration, resulting in a comparatively complex absorption spectrum involving more absorption peaks and transparency windows.[24]Additionally,four-level systems provide more manipulation means for effective control of absorption,dispersion, and nonlinearity.[25]Thus, the Kerr nonlinearity can be greatly improved by selecting appropriate controllable parameters.[26,27]In a four-level inverted-Y coherent system,a large optical nonlinearity at the single photon level which leads to the phase shift overπin Rydberg excitons media was obtained.[28]Alotaibi and Sanders introduced double–double EIT in the four-level tripod-type system,and obtained a greatly enhanced nonlinear optical susceptibility in the region of the second transparency window.[29]Moreover, in the four-level N-type system, EIT can suppress the linear absorption and greatly enhance the nonlinear susceptibilities by increasing the Kerr nonlinearity by several orders of magnitude compared to the traditional three-level system.[30]Shenget al.studied the power of the additional switching beam to control the magnitude,as well as the sign of the Kerr nonlinearity in a four-level N-type atomic system.[31]Therefore,the four-level configurations are indeed an efficient model for nonlinear effects,with significant benefits over three-level configurations.
As the intensity of the coupling field increases, the EIT will be replaced by AT splitting.[32]Many works in previous papers for Kerr nonlinearity were based on the EIT system, whereas the work based on AT splitting was hardly reached.For AT splitting, the large nonlinear susceptibilities can be achieved with large coupling detunings and strong coupling fields, and need not worry about the loss of the probe field.These large nonlinear susceptibilities can effectively excite third-order nonlinear effects such as FWM and Raman effect.Literatures show that quantum entanglement based on FWM is related to such coherent systems with large detunings.[33,34]Glorieuxet al.proposed that the generation of FWM in a double-Λ system driven by a far-detuned pump,and obtained quantum-correlated beams.[34]It is worth noting that the double-Λ system is essentially a four-level N-type system even if the conjugate light is considered,where two pumps and a seed correspond to the three fields of the four-level Ntype system, respectively.Motivated by the above work, we apply strong coupling fields and large detunings to explore the Kerr nonlinearity and FWM of the four-level N-type system,and attempt to control of the nonlinearities by adjusting the detunings of the coupling fields.An important result of our study is that under AT splitting due to strong optical fields,far coupling detunings can lead to an increase of three orders of magnitude in the third-order nonlinearity and the associated FWM intensity.Our study may provide guidance for the achievement of strong FWM in experiments.In addition,this work can contribute to a systematic understanding of the linear and nonlinear properties of the four-level N-type system.
In this paper,we set up the probe field to be coupled to a transition of the four-level N-type system,allowing the probe field to balance both the three-level Λ-type EIT scheme and the three-level V-type EIT scheme.To begin with, we study the absorption spectra under the combined contributions of the Λ-type system and the V-type system,taking into account the EIT in the weak coupling fields and the AT splitting in the strong coupling fields.Afterwards,we examine the Kerr nonlinearity using an iterative method based on perturbation theory.We discuss in detail the enhancement of the Kerr nonlinearity under large detunings of the coupling fields and finally investigate the FWM associated with the Kerr nonlinearity.
2.Theoretical model and calculation
The four-level N-type system is shown in Fig.1, which can be formed by atomic Rubidium87Rb.The hyperfine levels 52S1/2,F= 1 and 2 of87Rb are chosen to be|1〉 and|3〉, 52P1/2,F=1 to be|2〉 and 52P3/2,F=2 to be|4〉, respectively.The weak probe fieldεpwith a frequency ofωpis used for the atomic transition between levels|2〉and|3〉,with a corresponding Rabi frequency of 2?p=μ23·εp/The control fieldεcwith a frequency ofωcand the signal fieldεswith a frequency ofωsare used for the atomic transitions|2〉-|1〉 and|4〉-|3〉, with corresponding Rabi frequencies of 2?c=μ21·εc/and 2?s=μ43·εs/,respectively.Here,μijdenote the dipole moments of the atomic transitions, andεicorrespond to the electric field amplitudes.The spontaneous decay rates from|2〉to|3〉,|4〉to|3〉, and|2〉to|1〉are 2γ23,2γ43, and 2γ21, respectively.The relaxations of|1〉to|3〉and|2〉to|4〉are 2γ13and 2γ24,respectively.
In the interaction picture, the Hamiltonian under the dipole and rotation-wave approximation is given by
in whichδ=ωp-ω23,?c=ωc-ω21and?s=ωs-ω43are the detunings of the probe, control and signal fields, respectively,andωijis the atomic transition frequency between levels|i〉and|j〉.The dynamic evolution of the system is governed by the master equation of the density matrix
here,Λρrepresents the atomic damping to the background modes andρis the density matrix operator.The density matrix equations of motion can be written as
whereM22=-2(γ21+γ23+γ24),M43= i?s-γ43,M42=-[i(δ-?s)+(γ21+γ23+γ43+γ24)],M41=-[i(δ-?c-?s)+(γ43+γ13)],M32=-[iδ+(γ21+γ23+γ24)],M31=-[i(δ-?c)+γ13],M21=[i?c-(γ21+γ23+γ24+γ13)].The above equations are constrained byρ11+ρ22+ρ33+ρ44=1 andρ*ji=ρij.


The solutions of the zeroth-order density matrix equations provide the constant terms for the first-order density matrix equations,thus making the first-order density matrix equations solvable and leading to a unique and deterministic solution.Similarly, the solutions of thei-th-order density matrix equations provide the constant terms for the(i+1)-th-order density matrix equations, making the (i+1)-th-order density matrix equations solvable.Thei-th-order density matrix equations are as follows:


3.Results and discussion
3.1.Analysis of linear absorption
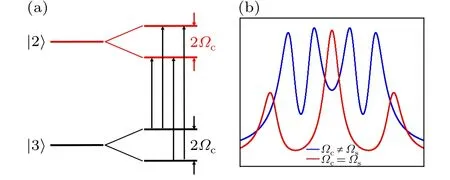
EIT converts to AT splitting in the increase of the coupling fields.Figure 2 shows the absorption of the probe field at different?c.In Fig.2(a), there are three absorption peaks and two transparent windows at?s=1.The central peak is the strongest, forming an EIA, with the two equal peaks on both sides being lower than the EIA.Here neither?cnor?sleads to complete energy level splitting or complete quantum coherence,so quantum coherence and AT splitting exist simultaneously.In this case,if we consider partial AT splitting,the absorption of the triple-peaked frame can be easily explained.As?c=2,level|2〉undergoes a strong AT splitting and forms two sets of V-type EIT systems with levels|3〉and|4〉,but owing to the weak coherence of the V-type system(?s=1),weak EITs appear at the absorption peaks on both sides.Therefore,as?cincreases,the AT splitting increases and the transparent window at the resonance becomes wider and deeper,while the weak EITs on both sides are maintained.The above discussion is the probe absorption at?s=1, where both quantum coherence and AT splitting are possible and the situation is relatively complicated.The following discussion turns to the probe absorption at?s=5, as shown in Fig.2(b), where the AT splitting plays an important role.We find that the probe absorption spectra show four peaks as?c=1,2,3,4,and the transparent windows on both sides of the absorption spectra widen with the increasing?c.Contrastly, as?c=5, triple peaks appear for the probe absorption spectra, and the height of the central peak is twice than that of the two side bands.Figure 4 provides an explanation for the cause of the above absorption spectra.The AT splitting of levels|2〉and|3〉depends on?cand?s,and their splitting widths are 2?cand 2?s,respectively, so that the sub-transition from|3〉to|2〉will have four transition paths,as shown in Fig.4(a).As?c=?s,two of the four transition paths have equal frequencies,eventually leading to three absorption peaks, with the central absorption peak being twice as high as either peaks;while?c/=?s,four absorption peaks appear corresponding to four transition paths with different frequencies,as shown in Fig.4(b).
The impact of the changes in?son the absorption of the probe field is shown in Fig.3.The absorption at?c=1 and?s=1 in Fig.3(a) is consistent with Fig.2(a).As?sincreases, the level|3〉 splits, but?c/=?sleads to the inconsistency of the two splits of levels|2〉 and|3〉, forming four absorption peaks.Although as?s= 2, it still shows three absorption peaks, the central absorption peak is a partial superposition of two adjacent absorption peaks.Since?cis unchanged, the transparent windows on either side remain constant and the distance between the two EIT windows is 2?s.The probe absorption at?c=5 is shown in Fig.3(b), it is doubtless that there is a significant AT splitting at the level|2〉.First, as can be seen, the probe absorption at?s=1 is the same as in Fig.2(a).As?s=2,3,4,the AT splitting at level|3〉becomes clear.As is mentioned,since?c/=?s,the splitting is unequal,thus leading to four absorption peaks.Finally,at?s=5,this case is consistent with Fig.2(b).
In a word, the number of absorption peaks is closely related to the AT splitting,when the splits of upper level|2〉and lower level|3〉 are identical, two of the four transition paths have equal transition frequencies, and the probe absorption shows three peaks; if the splits of upper level|2〉 and lower level|3〉are not identical,the probe absorption usually shows four peaks,and the distance between a pair of peaks always remains twice of the Rabi frequency of the corresponding field.Since?cdetermines the splitting of upper level|2〉 and?sdetermines the splitting of lower level|3〉, it shows three absorption peaks for?c=?sand partially four absorption peaks for?c/=?s.The schematic diagram of the AT splitting is given in Fig.4(a),and the corresponding absorption spectra at?c=?sand?c/=?sare shown in Fig.4(b).
3.2.Analysis of Kerr nonlinearity
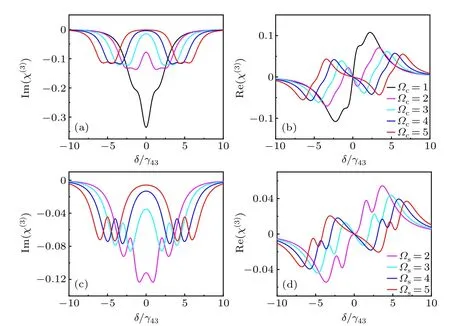
Using iterative calculations,we can obtain the Kerr nonlinearity of the system.Figure 5 displays the imaginary and real parts of the Kerr nonlinear susceptibility.The Kerr nonlinear absorption and nonlinear coefficients for different?cat?s=1 are given in Figs.5(a)and 5(b).It can be observed that when?c=1, the Kerr nonlinear absorption exhibits strong nonlinear gain at the zero probe detuning,which corresponds to an EIA in the linear absorption as shown in Fig.2(a).As?cincreases, quantum coherence weakens, and AT splitting increases,and consequently the gain at the zero probe detuning decreases,corresponding to an increasingly large transparency window in the linear absorption also as shown in Fig.2(a).Each nonlinear absorption shows four gain peaks, with faint concave gains on both sides corresponding to the weak EITs in the linear absorption.Overall, the gain in the Kerr nonlinearity corresponds to the absorption in its absorption spectrum,which reflects the reverse relationship between the Kerr nonlinearity and the linear absorption spectrum.Figure 5(b)shows the real part of the Kerr nonlinear susceptibility under the same conditions.It can be observed that there is a strong Kerr nonlinear coefficient at?s=?c=1, corresponding to the strong quantum coherence from the EIA.The rest of the Kerr nonlinear coefficients have double rounds of dispersion and satisfy the Kramers–Kronig relations with the imaginary part.The variation of the Kerr nonlinear absorption and the Kerr nonlinear coefficient with?sat?c= 1 are shown in Figs.5(c) and 5(d).Since the case?s=1 is consistent with Fig.5(a), it is not discussed here to avoid repetition.From Fig.5(c), it can be observed that for?s=2, there are four gain peaks, with the pair in the midest partially overlapping,corresponding to the overlap of two peaks in the linear absorption as shown in Fig.3(a).As?sincreases,there are still four gain peaks, but the distance between the central pair of peaks increases, correlating to the AT splitting caused by?s.The evident gain concaves on both sides are a result of the EIT or AT splitting of the Λ system consisting of levels|1〉,|2〉and|3〉.In the Kerr nonlinear coefficient shown in Fig.5(d), the quadruple rounds change can be observed,and also satisfy the Kramers–Kronig relations with its imaginary part.
3.3.Enhanced Kerr nonlinearity and FWM
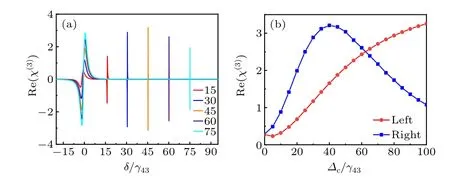
Motivated by Ref.[34], the nonlinear effect of strong four-wave mixing can be excited via far detunings of the coupling fields in the four-level N-type system.Here,we focus on the effect of large detuning of the optical field on the Kerr nonlinearity.In Figs.6(a) and 6(b), the signal detuning is given by 100 and the control detuning by 15,30,45,60,75,respectively, with identical Rabi frequencies of 5 for the coupling fields.We find that two dispersions occur,one of which gradually approaches the resonance position of the probe field with the growth of the control detuning, while the other is sharper and its position depends on the control detuning,both of them showing normal dispersion.The amplitude of the dispersion for the former gradually increases with the growth of the control detuning,while that of the latter has an increase in the first period and then followed by a decrease, with the inflection point being at?c=40,as shown in Fig.6(b).It indicates that the significantly enhanced Kerr nonlinearity can be obtained via large detunings of the control field, and the Kerr nonlinearity can be managed by adjusting the two detunings of the coupling fields.
The Kerr nonlinearity is also correlated with an FWM or Raman effect, and we useto describe the FWM process.[36]For many cases, for example, a degenerate two-level atomic system, the control and signal fields are a common field,in which case the detuning of the control and signal fields remains identical.[37]Figure 7 shows the evolution of the FWM with the variation of the equal detunings of the control and signal fields.It is evident that there are two peaks for the FWM,with one being sharp and the other being normal.The sharp one occurs at the position ofδ=?c,whose peak value grows with the increase of the detuning?c(s)in the graph.The other otherwise happens beside the resonant position of the probe field, whose peak value also increases with the growth of the detuning?c(s),and whose position gradually moves towards the resonant position of the probe field.To illustrate the effect of the detunings?c(s)on the intensity of the FWM,we define the parameterQbeing the ratio of the intensity of FWM with the detuning to that without the detuning.Figure 7(b) provides the ratioQas a function of the detunings?c(s)for the FWM intensity for the normal one.As?c(s)are small, e.g.,?c(s)=1, the ratio is about 2.2.As?c(s)increases,the ratio increases rapidly,reaching 34 for?c(s)=10 and reaching 105 for?c(s)=20.However, as?c(s)increases further,the growth rate slows down,and at?c=200,the ratio is as high as 495.This fact indicates that a significant FWM can be achieved via providing large detunings of the coupling fields in the present atomic system,and thus the intensity of the FWM can be managed by adjusting the coupling detunings.
4.Conclusion
We have explored the linearity and the nonlinearity of the four-level N-type coherent system.As the two coupling fields are weak,the absorption spectrum is principally influenced by EIT or EIA,and as the two coupling fields are strong,the absorption spectrum is controlled by the AT splitting.A threepeak absorption spectrum has emerged as the Rabi frequencies of the two coupling fields are equal,while a four-peak absorption spectrum has turned up as the Rabi frequencies of the two coupling fields have a big difference.We have found that the Kerr nonlinear absorption has an opposite behaviour to the linear absorption under the same condition.Although the Kerr nonlinearity is small as the detunings of the coupling fields are small, it can reach a growth of three orders of magnitude at large detunings of the coupling fields.Using the detunings of the coupling fields, we can control the Kerr nonlinearity and the intensity of the FWM.The proposed FWM scheme provides a practical approach for the experimental preparation of squeezed states and multipartite entanglement in an atomic system.
Acknowledgment
Project supported by the Open Subject of the State Key Laboratory of Quantum Optics and Quantum Optics Devices(Grant No.KF202209).
- Chinese Physics B的其它文章
- The application of quantum coherence as a resource
- Special breathing structures induced by bright solitons collision in a binary dipolar Bose–Einstein condensates
- Effect of short-term plasticity on working memory
- Directional-to-random transition of cell cluster migration
- Effect of mono-/divalent metal ions on the conductivity characteristics of DNA solutions transferring through a microfluidic channel
- Off-diagonal approach to the exact solution of quantum integrable systems

