Straight and twisted Weyl nodal line phonons in Ho2CF2 material
Xin-Yue Kang(康鑫越), Jin-Yang Li(李金洋), and Si Li(李思),?
1School of Physics,Northwest University,Xi’an 710127,China
2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China
Keywords: topological quasiparticles,topological phonons,straight nodal lines,twisted nodal lines
1.Introduction
In the past decade, there has been a significant surge of research interest in the topological quasiparticles that emerge around band degeneracy points in condensed matter systems.[1–3]Based on the dimension of the band degeneracy within the Brillouin zone(BZ)in momentum space,topological quasiparticles can be categorized as zero-dimensional(0D)node points (such as Weyl and Dirac semimetals),[4–8]onedimensional(1D)nodal lines[9–19]and two-dimensional(2D)nodal surfaces.[20–23]Due to these degeneracies in topological quasiparticles, the low-energy electron excitations are endowed with various exotic physical properties.
Topological quasiparticles were studied in electronic band structures at first and then the study was extended to bosonic and even classical systems, such as photonic crystals,[24–26]acoustic systems,[27–29]and electric circuit networks.[30–32]Phonons are the fundamental bosonic excitations in a crystal material,describing the collective motion of an atomic lattice.Unlike electronic fermions,phonons are not constrained by the Pauli exclusion principle.Consequently,the entire frequency range of a phonon spectrum can be experimentally explored.Recently,topological quasiparticles in phonons have been attracting a great deal of attention.[33–42]
As an interesting type of topological quasiparticles,topological nodal line semimetals, which are band degeneracy curves between the conduction and valence bands in a BZ,have been attracting significant interest due to their variety of intriguing properties, such as drumhead-like surface states,[10]anisotropic electron transport,[12]an unusual optical response and circular dichroism,[43–45]possible surface magnetism and superconductivity,[16,46–48]and density fluctuation plasmons and Friedel oscillations.[49]In addition, topological nodal lines can be classified into various types based on their geometry, such as nodal rings,[13–15]nodal chains,[50,51]nodal links,[52–54]and even nodal knots.[55,56]These topological nodal lines all have closed configurations.Recently,straight nodal lines and twisted nodal lines that extend in a certain direction and traverse the entire bulk BZ have been discovered, and several concrete materials hosting such nodal lines have been proposed.[18,38,57–60]However, the number of candidates is still very limited.Hence,there is a need to explore more realistic materials that can realize straight and twisted Weyl nodal lines.
In this work, through first-principles calculations and symmetry analysis,we report that Ho2CF2material hosts both straight Weyl nodal lines and twisted Weyl nodal lines in its bulk phonon spectrum.We find that the crossing points between the top two phonon bands form two straight Weyl nodal lines at the BZ boundary and six twisted Weyl nodal lines within the BZ.Here, all the straight and twisted Weyl nodal lines extend along thekzdirection and across the entire BZ and they are topologically distinct from those which do not penetrate the BZ.The results of symmetry analysis and the nontrivialπBerry phase are demonstrated.The corresponding nontrivial surface states are revealed.We also construct a tight-binding (TB) model to capture these nodal lines.Our findings suggest an exceptionally suitable platform for experimentally exploring the intriguing properties of straight and twisted Weyl nodal line phonons.
2.Crystal structure
Ho2CF2belongs to the rare earth carbide fluoride compounds and it has been successfully synthesized in experiments.[61]The crystal structure has been determined by a quantitative analysis of the x-ray diffraction data(the crystal structure data area=b=3.6567 ?A andc=6.3171 ?A).[61]Ho2CF2crystalizes into a trigonal structure with space group No.164 (P3m1), which can be generated by the following symmetry elements:S+6andC′′2.The crystal structures of Ho2CF2and the BZ are schematically shown in Fig.1.The Wyckoff positions of the Ho,C and F atoms are 2d(1/3,2/3,0.2098),1a(0,0,0)and 2d(1/3,2/3,0.6175),respectively.
3.First-principles methods
The density functional theory (DFT) was employed for first-principles calculations,utilizing the projector-augmented wave method as implemented in the Viennaab initiosimulation package.[62–64]The exchange–correlation functional employed the Perdew–Burke–Ernzerhof[65]realization within the generalized gradient approximation.The plane wave energy cutoff was set to 600 eV and the BZ was sampled using aΓcenteredkmesh of size 15×15×8.The convergence criteria for energy and force were set to 10-7eV and 10-3eV/?A,respectively.The structure is fully optimized.The optimized lattice parameters for the Ho2CF2area=b=3.638 ?A andc=6.416 ?A,which are close to the experimental values(a=b=3.6567 ?A andc=6.3171 ?A).The force constants and phonon spectra were obtained using the density functional perturbation theory in combination with the Phonopy package.[66]The irreducible representations of the phonon spectra were calculated using the PhononIrep package.[67]The surface states were calculated using the Green’s function method based on the WannierTools package.[68–70]
4.Results
4.1.Straight and twisted Weyl nodal line phonons
The phonon spectrum of Ho2CF2obtained from firstprinciples calculations is shown in Fig.2(a).From Fig.2(a),one can observe that three phonon bands(the 13th to the 15th bands) between 10.8 THz and 18 THz separate from other phonon bands and entangle together.Among the three phonon bands, the crossing between the top two phonon bands (14th and 15th)forms a twofold degenerate along theK–Hpath and linear band-crossing points along theΓ–KandH–Apaths.Via a careful scan of the BZ,we find that these degenerate points form two straight Weyl nodal lines along pathsK–HandK′–H′at the BZ boundary and six twisted Weyl nodal lines within the BZ, as shown in Figs.2(b) and 2(c), respectively.Particularly, the phonon band structure around the straight and twisted Weyl nodal lines is very ”clean”, since the crossing points of the nodal lines are located in the gap between the 14th and 15th phonon bands and there are no other extraneous bands nearby.Meanwhile, the nodal lines are exposed in a large frequency window with a width of about 1 THz.The frequency of the nodal lines can be inferred from the dip in the phonon density of states.The clean phonon band structure,the large frequency window and the small frequency variation on the nodal lines make Ho2CF2an almost ideal candidate for experimental studies of straight and twisted Weyl nodal line phonons.

Here, both the straight and twisted Weyl nodal lines traverse the whole BZ in thekzdirection.This type of nodal line is topologically different from those that do not traverse the BZ because the former cannot be continuously contracted to a point,while the latter can.Mathematically,the BZ is topologically equivalent to a three-dimensional torus denoted as T3.Closed loops on T3can be categorized based on their fundamental homotopy groupπ1(T3)=Z3, which is described by three integers representing the number of times the loop winds around each of the three directions.[18]From this perspective,the nodal lines that do not traverse the BZ belong to the trivial class withZ3=(0,0,0), while the nodal lines discussed here belong to the class(0,0,1).
Since the straight and twisted Weyl nodal lines extend along thekzdirection and display strong anisotropy in the dispersion relation, they may result in pronounced anisotropic transport.
4.2.Symmetry protection and Berry phase
The straight Weyl nodal lines along pathsK–HandK′–H′are protected by two independent symmetries:PTsymmetry andC3zsymmetry.Phonons are intrinsically spinless and the presence ofPTsymmetry requires that the Berry phase associated with any closed path must be quantized into multiples ofπ.[71]In this context,the Berry phase is given by the equation
Here,the Berry phase is computed for a locally gapped spectrum along a closed path?.The term|un(k)〉 represents the periodic part of the Bloch eigenstate.For a nodal line,we can calculate its Berry phaseγ?for a closed path?encircling the nodal line.Through DFT calculations,we find that the Berry phases for the straight Weyl nodal lines along pathsK–HandK′–H′are-πandπ[see Fig.2(b)],respectively,showing that the straight nodal lines are topologically nontrivial.

Similarly, the twisted Weyl nodal lines are protected by thePTsymmetry andC′′2symmetry.ThePTsymmetry requires that the Berry phase for any closed path encircling the twisted Weyl nodal line is±π,which is also confirmed by our DFT calculations, as shown in Fig.2(c).The two crossing phonon bands near the nodal point on the twisted Weyl nodal line have different IRRsAandB[along the pathΓ–KandH–A,as shown in Fig.2(a)],which correspond to the oppositeC′′2eigenvalue 1 and-1.
4.3.Drumhead-like surface states
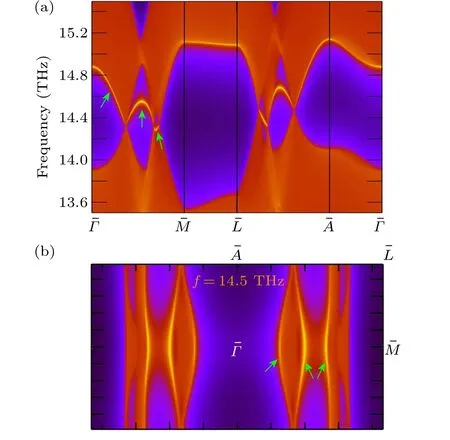
One of the important signatures of the topological nodal line is the presence of drumhead-like surface states at the sample surface.[10]In Fig.3,we plot the calculated surface phonon spectrum for the (100) surface of Ho2CF2.One indeed observes a surface band connecting the nodal points that correspond to the nodal line in the bulk, as indicated by the green arrows in Fig.3.The surface band connects the nodal lines through the surface BZ boundary.We also plot the isofrequency surface contour at 14.5 THz of the (100) surface in Fig.3(b).
4.4.TB model
To further characterize the straight and twisted Weyl nodal lines,we construct a TB model based on the symmetry requirements.We consider one atom occupying the Wyckoff position 1a(0, 0, 0) within a unit cell with three p-like basis orbitals(px,py,and pz)in each site.We consider the nearestneighbor hopping,the spinless TB model is constructed using the MagneticTB package[72]and the model is given by
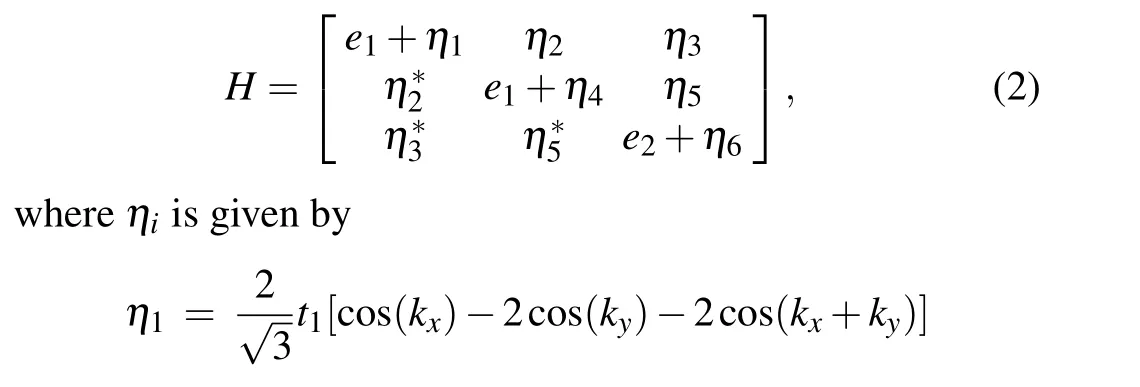
whereei,tiare real model parameters and the wave vectors are measured in units of the respective inverse lattice constant.The phonon bands calculated by the TB model are shown in Fig.4,which shows that our TB model accurately captures the dispersion features of the straight and twisted Weyl nodal line phonons in Ho2CF2.

5.Conclusion
In conclusion, we have theoretically predicted the existence of both straight and twisted Weyl nodal line phonons in Ho2CF2.These nodal lines traverse the whole BZ along thekzdirection.The results of the symmetry analysis and Berry phase calculations indicated that these nodal lines have symmetry protection and are topologically nontrivial.In addition,drumhead-like surface states occur on the (100) surface.We have constructed a TB model to describe these nodal lines.In an experiment, the bulk straight and twisted Weyl nodal line phonons can be directly probed in neutron scattering[73]and x-ray scattering[74](for example,the helical nodal lines in the phonon spectrum of MoB2have been probed by inelastic xray scattering[38]), and the surface states could be probed by high-resolution electron energy loss spectroscopy,[75]helium scattering,[76]and THz spectroscopy.[77,78]Our results offer a promising platform for exploring the intriguing physics associated with straight and twisted Weyl nodal line phonons.
Acknowledgment
Project supported by the National Natural Science Foundation of China(Grant No.12204378).
- Chinese Physics B的其它文章
- The application of quantum coherence as a resource
- Special breathing structures induced by bright solitons collision in a binary dipolar Bose–Einstein condensates
- Effect of short-term plasticity on working memory
- Directional-to-random transition of cell cluster migration
- Effect of mono-/divalent metal ions on the conductivity characteristics of DNA solutions transferring through a microfluidic channel
- Off-diagonal approach to the exact solution of quantum integrable systems

