胡建軍,王 偉,李恒杰

(蘭州文理學(xué)院 數(shù)字媒體學(xué)院, 甘肅 蘭州 730010)

Smart[1]提出一種有效的在跡1橢圓曲線上求解離散對數(shù)的方法,Monnerat[2]較為詳細(xì)地描述了跡1橢圓曲線上求解離散對數(shù)的實(shí)施方法,Bradley[3]介紹了跡1橢圓曲線上求解離散對數(shù)的具體實(shí)踐. 20多年來,學(xué)者們針對跡1橢圓曲線的理論研究較多[4-6],這些研究成果對于信息安全和密碼學(xué)的應(yīng)用起到了積極的作用,然而學(xué)者們對跡1橢圓曲線的攻擊實(shí)踐研究關(guān)注度不夠,對于理解和應(yīng)用跡1的橢圓曲線的研究也是不夠的[7-9].

在跡1橢圓曲線上求解離散對數(shù)的實(shí)質(zhì)是利用擴(kuò)域上點(diǎn)的扭曲特征,通過約減和形式對數(shù)理論解決離散對數(shù)問題[10-12].為了較好地理解跡1橢圓曲線的理論成果及了解算法攻擊的實(shí)施過程和效果,論文給出求解離散對數(shù)的實(shí)踐方法,利用Hensel提升理論,將素?cái)?shù)域Fp的點(diǎn)提升到p上,再通過約減和形式對數(shù)的方法求解離散對數(shù)問題,分析了該方法的計(jì)算效率,最后通過實(shí)例驗(yàn)證了該方法的正確性和有效性.

1 橢圓曲線的性質(zhì)及Nigel Smart攻擊

1.1 橢圓曲線的性質(zhì)

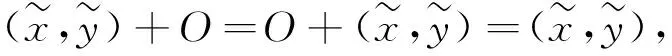
(1)

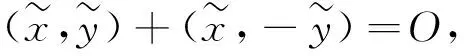
(2)

(3)

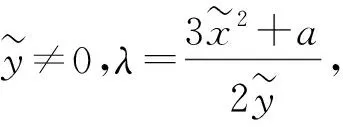
x3=μ2-x1-x2,(x1,y1)+(x2,y2)=(x3,μ(x1-x3)-y1),

(4)

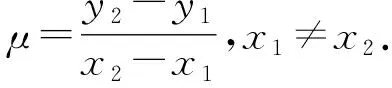
性質(zhì)1橢圓曲線的跡與階滿足N=p+1-t,其中t為橢圓曲線的跡.

跡為1的橢圓曲線稱為反常曲線(anomalous).反常曲線的階等于點(diǎn)的個數(shù),即N=p.

定義域K的最小素?cái)?shù)子域的階稱為域K的特征,記為char(K).

因?yàn)橛欣頂?shù)域和實(shí)數(shù)域不存在最小素?cái)?shù)子域,因此有理數(shù)域和實(shí)數(shù)域的特征為0.

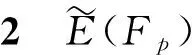
性質(zhì)3設(shè)p是p-adic下的有理數(shù)域,則char(p)=0.

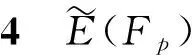
1.2 Nigel Smart攻擊

設(shè)E(p)是的擴(kuò)域,p),Q∈E(p),P和Q是和的縱坐標(biāo)的Hensel提升,Q-mP=R∈E1(p).

Nigel Smart攻擊過程基于如下事實(shí)

特別地,有

定義

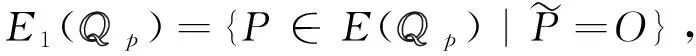
則

有

pQ-pmP=pR∈E2(p).

(5)

定義兩個映射

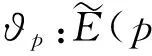
(6)

ψp:E1(p)→pp,P

(7)

用ψ映射對式(5)兩邊的每一項(xiàng)取p-adic橢圓曲線對數(shù),得

ψp(pQ)-mψp(pP)=ψp(pR)≡0(modp2),

(8)

(9)

由式(6)的定義,得

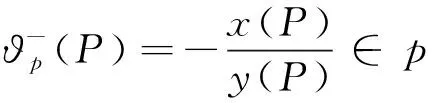
(10)

其中:x(P)和y(P)分別表示點(diǎn)P的橫坐標(biāo)和縱坐標(biāo).

由式(7),(10),得

(11)

利用式(9),(11)可以快速求解跡1橢圓曲線的離散對數(shù).

1.3 點(diǎn)的Hensel坐標(biāo)提升

令f(x,y)=y2-x3-ax-b,則f(x,y)≡0(modp).由于橢圓曲線p上的元素的坐標(biāo)值都落在[0,p2)之內(nèi),因此用O(p3)做點(diǎn)的坐標(biāo)的邊界,選擇點(diǎn)和p上橫坐標(biāo)x的值相同.由Hensel提升理論可知,點(diǎn)的縱坐標(biāo)y的p-adic擴(kuò)張為y=c0+c1p+c2p2+….由于

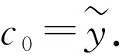
故

故

2 算法分析與設(shè)計(jì)

提升橢圓曲線點(diǎn)的目的是利用橢圓曲線的扭曲點(diǎn)求解離散對數(shù)問題.由點(diǎn)坐標(biāo)邊界O(p3)可知,可以將一個坐標(biāo)表示成一個3元組(h1,h2,h3).p-adic數(shù)的冪的范圍為[-3,2].

根據(jù)p-adic數(shù)的除法運(yùn)算法則,分母最左邊的第一個數(shù)不能為零,因?yàn)榱銢]有乘法逆元,因此,當(dāng)分母最左邊的第一個數(shù)為零時,需要移位解決,這樣一來,坐標(biāo)計(jì)算中的一些相關(guān)變量也要隨之移位處理.為了能夠處理相關(guān)變量,式(3),(4)中的斜率公式只能用分?jǐn)?shù)表示.

在pP或pQ的運(yùn)算中,由于p是奇數(shù),因此最終一步只能是做加法運(yùn)算才能使點(diǎn)投射到無窮遠(yuǎn)點(diǎn).在這種情形下,只有考慮加法斜率中分母最左邊的第一個數(shù)為零的情形.當(dāng)加法斜率中分母最左邊的第一個數(shù)不為零時,坐標(biāo)中與斜率無關(guān)的變量不受影響,因此其他變量不做移位處理;當(dāng)加法斜率中分母最左邊的第一個數(shù)為零時, 坐標(biāo)中與斜率無關(guān)的變量都受影響,因此,其他變量要根據(jù)零的個數(shù)做從左向右移位的處理,零的個數(shù)為移位的次數(shù),處理的方式是每個與分母無關(guān)的變量乘以分母;最后做加法運(yùn)算(減法轉(zhuǎn)換成負(fù)數(shù)做加法運(yùn)算).點(diǎn)運(yùn)算根據(jù)兩個是否相同,給出式(12),(13)兩種表達(dá)式.

倍點(diǎn)坐標(biāo)計(jì)算公式

(12)

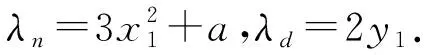
點(diǎn)加坐標(biāo)計(jì)算公式

(13)

其中:μd(1)表示分母的第一個值,μn=y2-y1,μd=x2-x1.

根據(jù)最后一次計(jì)算到無窮遠(yuǎn)點(diǎn)的加法運(yùn)算可知,x的坐標(biāo)表達(dá)式形式為c-2p-2+c-1p+c0+O(p),y的坐標(biāo)表達(dá)式形式為c-3p-3+c-2p-2+c-1p+O(p0).

兩個p-adic數(shù)的3元組,相乘需要2次加法,相除需要6次加法,如果將p-adic數(shù)的加法記為一次基本運(yùn)算,則上述算法做一次點(diǎn)運(yùn)算共需24次加法運(yùn)算.根據(jù)“平方乘”算法,進(jìn)行pP或pQ點(diǎn)運(yùn)算的次數(shù)為log2p,從而整個算法進(jìn)行p-adic數(shù)運(yùn)算的時間復(fù)雜度為O(24log2p+6),兩個點(diǎn)需要的存儲空間為12p.如果p按照160位長度計(jì)算,計(jì)算兩個點(diǎn)需要240個字節(jié)的存儲空間.

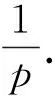
3 實(shí)例驗(yàn)證與分析

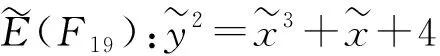
O,(0,2),(0,17),(1,5),(1,14),(5,1),(5,18),(6,6),(6,13),(8,7),(8,12),(9,1),(9,18),(10,8),(10,11),(11,4),(11,15),(14,8),(14,11).

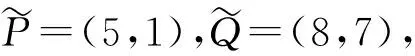
P=(5+O(193),1+13·19+10·192+O(193)),

Q=(8+O(193),7+14·19+3·192+O(193)).

19P的計(jì)算過程如下

2P=(9+18·19+3·192+O(193),18+16·19+18·192+O(193)),

4P=(8+1·19+10·192+O(193),12+16·19+11·192+O(193)),

8P=(14+5·19+12·192+O(193),11+2·19+3·192+O(193)),

9P=(1+12·19+O(193),14+6·192+O(193)),

18P=(5+7·19+10·192+O(193),18+5·19+16·192+O(193)),

19P=(9·19-2+12·19-1+O(190),8·19-3+5·19-2+O(19-1)),

同理計(jì)算出19Q點(diǎn)的坐標(biāo)

上述過程結(jié)果與文獻(xiàn)[3]有較大差異,主要是第2個及以后的數(shù)均不相同,但最終結(jié)果是相同的.文獻(xiàn)[3]沒有給出計(jì)算過程及結(jié)果,因此很難與其做對比.

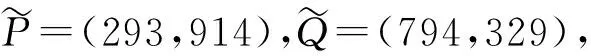
P=(293+O(1 0193),914+308·1 019+857·1 0192+O(1 0193)),

Q=(794+O(1 0193),329+561·1 019+465·1 0192+O(1 0193)).

1 019P的計(jì)算過程如下

3P=(885+847·1 019+794·1 0192+O(1 0193),113+714·1 019+435·1 0192+O(1 0193)),

6P=(483+668·1 019+953·1 0192+O(1 0193),97+700·1 019+694·1 0192+O(1 0193)),

7P=(763+808·1 019+701·1 0192+O(1 0193),442+454·1 019+917·1 0192+O(1 0193)),

14P=(248+611·1 019+319·1 0192+O(1 0193),862+959·1 019+619·1 0192+O(1 0193)),

15P=(353+538·1 019+99·1 0192+O(1 0193),741+48·1 019+76·1 0192+O(1 0193)),

30P=(582+332·1 019+79·1 0192+O(1 0193),208+723·1 019+209·1 0192+O(1 0193)),

31P=(349+76·1 019+180·1 0192+O(1 0193),526+940·1 019+880·1 0192+O(1 0193)),

62P=(451+226·1 019+490·1 0192+O(1 0193),763+328·1 019+617·1 0192+O(1 0193)),

63P=(87+315·1 019+351·1 0192+O(1 0193),396+731·1 019+759·1 0192+O(1 0193)),

126P=(16+325·1 019+162·1 0192+O(1 0193),851+618·1 019+575·1 0192+O(1 0193))

127P=(564+707·1 019+349·1 0192+O(1 0193),339+147·1 019+370·1 0192+O(1 0193)),

254P=(334+597·1 019+257·1 0192+O(1 0193),207+785·1 019+585·1 0192+O(1 0193)),

508P=(747+42·1 019+399·1 0192+O(1 0193),416+490·1 019+969·1 0192+O(1 0193)),

509P=(430+834·1 019+175·1 0192+O(1 0193),162+462·1 019+440·1 0192+O(1 0193)),

1 018P=(293+645·1 019+542·1 0192+O(1 0193),105+402·1 019+651·1 0192+O(1 0193)),

1 019P=(867·1 019-2+309·1 019-1+O(1 0190),950·1 019-3+557·1 019-2+O(1 019-1)),

同理計(jì)算出1 019Q點(diǎn)的坐標(biāo)

1 019Q=(210·1 019-2+952·1 019-1+O(1 0190),300·1 019-3+872·1 019-2+O(1 019-1)),

305·1 019+632·1 0192+O(1 0193),

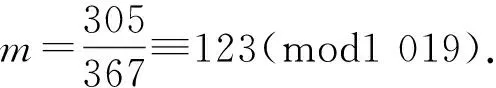
上述過程結(jié)果與文獻(xiàn)[2]有較大差異, 主要是第2個及以后的數(shù)均不相同,但最終結(jié)果是相同的.實(shí)例1的域空間大小比實(shí)例2小,但是無論兩個實(shí)例的域空間大小如何,計(jì)算結(jié)果都是正確的,這說明算法是正確和有效的.

4 結(jié)束語

文中給出了Nigel Smart思想的攻擊過程,其中實(shí)例部分通過C++編程實(shí)現(xiàn).文章解決了如何通過實(shí)踐去理解和應(yīng)用研究成果,同時該方法對于橢圓曲線的安全性的研究具有一定的參考價值.