二維連續(xù)型隨機(jī)變量函數(shù)的獨(dú)立性探討
丁尚文, 寧榮健
(1. 合肥工業(yè)大學(xué) 宣城校區(qū)基礎(chǔ)部,安徽 宣城 242000; 2. 合肥工業(yè)大學(xué) 數(shù)學(xué)學(xué)院,合肥 230601)
0 引 言
對(duì)于二維隨機(jī)變量(X,Y),X和Y之間的內(nèi)在聯(lián)系是人們關(guān)注的問題之一.目前在大多教材中,只介紹了X和Y的獨(dú)立性以及相關(guān)性等問題,由此不能完全地反映X和Y之間的內(nèi)在聯(lián)系.目前,二維隨機(jī)變量(X,Y)函數(shù)的獨(dú)立性研究比較少,也只是在個(gè)別例題中出現(xiàn)驗(yàn)證某二維連續(xù)型隨機(jī)變量(X,Y)函數(shù)的獨(dú)立性,并沒有一般性的結(jié)論,因此本文將對(duì)二維連續(xù)型隨機(jī)變量函數(shù)(X,Y)函數(shù)的獨(dú)立性作一點(diǎn)探討.目的是進(jìn)一步豐富和完善相關(guān)教學(xué)內(nèi)容,為教師培養(yǎng)學(xué)生創(chuàng)新意識(shí)和能力提供素材.
設(shè)二維隨機(jī)變量(X,Y)的密度函數(shù)為
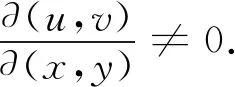
1 主要結(jié)論
為討論問題需要,先由《概率論與數(shù)理統(tǒng)計(jì)》教材[1]中定理3.7.4和文獻(xiàn)[2]中定理2得下列兩個(gè)引理.
引理1設(shè)二維隨機(jī)變量(X,Y)的密度函數(shù)為
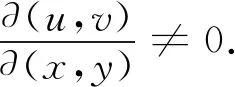
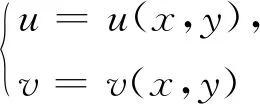
引理2二維隨機(jī)變量(X,Y)的密度函數(shù)為
其中D為單連通區(qū)域,f1(x,y)>0,則X和Y相互獨(dú)立的充要條件為D為正矩形區(qū)域,且f1(x,y)是可變量分離的.
引理2中,“f1(x,y)是可變量分離的”是指存在一元函數(shù)g(x)和h(y),使得f1(x,y)=g1(x)h(y).
由上述兩個(gè)引理即得
定理1在引理1中,若Duv為單連通區(qū)域,則U和V相互獨(dú)立的充要條件為Duv為正矩形區(qū)域,且g(u,v)是可變量分離的.
由定理1不難發(fā)現(xiàn)以下兩個(gè)問題:
一般而言,這并非易事,可根據(jù)區(qū)域D的特征采取一些變換.比如,如果D是矩形(未必是正矩形),可采取平移變換和旋轉(zhuǎn)變換將其變?yōu)檎匦?如果D是圓形區(qū)域,可采用平移變換和極坐標(biāo)變換將其變?yōu)檎匦?如果D是曲邊梯形區(qū)域,可考慮采用某些分式變換將其變?yōu)檎匦蔚?
如果找到U=u(X,Y),V=v(X,Y)同時(shí)滿足上面兩條,則U和V相互獨(dú)立,否則不相互獨(dú)立.由于涉及面太廣,本文從下面從幾個(gè)情形作一點(diǎn)探討.
情形一區(qū)域D:a 是可變量分離的.考慮到(X,Y)在D內(nèi)服從均勻分布,當(dāng)(u,v)∈Duv時(shí),f1(x(u,v),y(u,v))=常數(shù),因此g(u,v)=f1(x(u,v),y(u,v))|J|是可變量分離的. 作為結(jié)論1的應(yīng)用,下面列舉幾個(gè)例子. 為驗(yàn)證其正確性,對(duì)(ii)和(iv)通過直接求(U,V)的密度函數(shù)證明U和V相互獨(dú)立. (ii) 當(dāng)0 所以(U,V)的分布函數(shù)為 由引理2知U和V相互獨(dú)立. (iv) 當(dāng)0 所以(U,V)的分布函數(shù)為 由引理2知U和V相互獨(dú)立. 情形二 二維正態(tài)分布 證法1利用二維正態(tài)分布的性質(zhì)知,(U,V)服從二維正態(tài)分布.因此U和V相互獨(dú)立等價(jià)于U和V不相關(guān),即Cov(U,V)=0.由于DX=DY=1,Cov(X,Y)=ρ,進(jìn)而有 Cov(U,V)=Cov(aX+bY,cX+dY)=(ac+bd)+ρ(ad+bc)=0. 因此當(dāng)且僅當(dāng)(ac+bd)+ρ(ad+bc)=0時(shí),U和V相互獨(dú)立. 故當(dāng)且僅當(dāng)(ac+bd)+ρ(ad+bc)=0時(shí),g(u,v)可變量分離,從而U和V相互獨(dú)立. 證法1和證法2的結(jié)果完全吻合.從證明過程看,證法1比較簡(jiǎn)潔,這是由于證法1運(yùn)用了二維正態(tài)分布的性質(zhì),起點(diǎn)比較高. 情形三 圓盤區(qū)域內(nèi)的分布 對(duì)于圓盤區(qū)域可采取平移變換和極坐標(biāo)變換,可將變?yōu)檎匦螀^(qū)域.為方便起見,假定圓心在坐標(biāo)原點(diǎn),半徑為a(a>0). 結(jié)論3設(shè)二維隨機(jī)變量(X,Y)的密度函數(shù)為 由定理1即得R和Θ相互獨(dú)立. 作為結(jié)論3的應(yīng)用,有 (i) 若(X,Y)的密度函數(shù)為 則R和Θ相互獨(dú)立. 為驗(yàn)證其正確性,下面直接求(R,Θ)的密度函數(shù)來證明R和Θ相互獨(dú)立. 當(dāng)0≤r<1,0≤θ<2π時(shí),(R,Θ)的分布函數(shù)為 此時(shí)(R,Θ)的密度函數(shù)為 進(jìn)而可得(R,Θ)的密度函數(shù)為 由引理2知R和Θ相互獨(dú)立. (ii) 設(shè)(X,Y)的密度函數(shù)為 則R和Θ相互獨(dú)立. (iii) 設(shè)(X,Y)的密度函數(shù)為 則R和Θ相互獨(dú)立. 下面再討論一下二維正態(tài)分布N(0,0,1,1,ρ)在極坐標(biāo)變換下,R和Θ的獨(dú)立性問題. 當(dāng)ρ≠0時(shí),由于 不可分離變量,所以R和Θ不相互獨(dú)立. 當(dāng)ρ=0時(shí),由于 可分離變量,且區(qū)域0≤R<+∞, 0≤Θ<2π為正矩形區(qū)域,所以R和Θ相互獨(dú)立. 情形四 其他情況舉例 例1設(shè)隨機(jī)變量(X,Y)的密度函數(shù)為 是可變量分離的. 由定理1,U和V相互獨(dú)立. 由定理1,U和V相互獨(dú)立. 例3設(shè)平面區(qū)域D為x 對(duì)任意的實(shí)數(shù)a,b,求E(XaYb). 當(dāng)a+b≠-2,a-b≠0時(shí), 若b≠-1,則 若b=-1,有a≠-1,則 綜上,當(dāng)a+b≠-2,a-b≠0時(shí),有 同理可得 當(dāng)a+b≠-2,b-a=0,即a=b≠-1時(shí), 當(dāng)a+b=-2,b-a≠0時(shí),有b=-a-2,a≠-1, 當(dāng)a+b=-2,b-a=0,即a=b=-1時(shí), 故(U,V)的密度函數(shù)為 由定理1知U和V相互獨(dú)立,且其邊緣密度函數(shù)分別為 進(jìn)而求得 因此 二維連續(xù)型隨機(jī)變量內(nèi)在聯(lián)系的內(nèi)涵非常豐富,牽涉到諸多方面.本文只是對(duì)二維連續(xù)型隨機(jī)變量函數(shù)的獨(dú)立性問題做了一點(diǎn)探討,僅是冰山一角,而且研究尚不夠深入和完整.比如對(duì)于任意的二維連續(xù)型隨機(jī)變量(X,Y),是否均存在函數(shù)U=u(X,Y)和V=v(X,Y),使得U和V相互獨(dú)立?換言之,(X,Y)的密度函數(shù)f(x,y)具有什么樣的特征時(shí),才存在函數(shù)U=u(X,Y)和V=v(X,Y),使得U和V相互獨(dú)立?二維離散型隨機(jī)變量是否也有類似的結(jié)論?此外,對(duì)于二維隨機(jī)變量(X,Y),是否均存在函數(shù)U=u(X,Y)和V=v(X,Y),使得U和V不相關(guān)?以及還有哪些理論能夠更好地體現(xiàn)X和Y之間的內(nèi)在聯(lián)系. 作者借此拋磚引玉,歡迎大家積極參與到二維隨機(jī)變量內(nèi)在聯(lián)系的研究和挖掘中來,豐富概率論的理論和方法.鑒于作者水平有限,不足之處敬請(qǐng)各位同仁批評(píng)指正. 致謝作者非常感謝相關(guān)文獻(xiàn)對(duì)本文的啟發(fā)以及審稿專家提出的寶貴意見.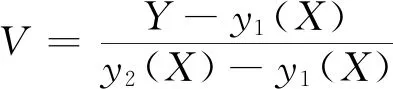
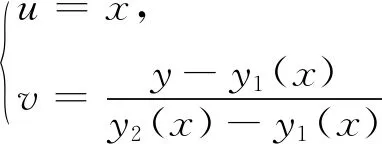
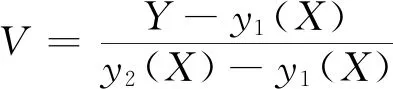
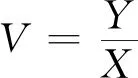
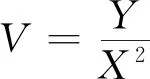
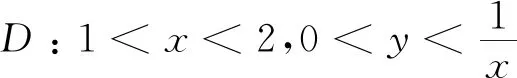
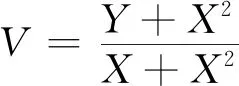
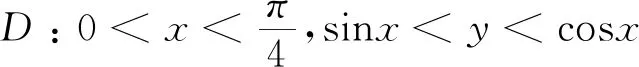

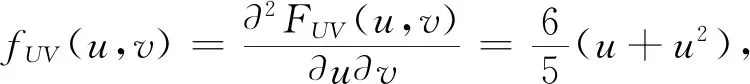
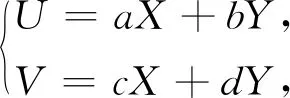
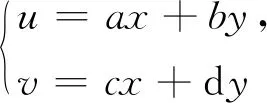
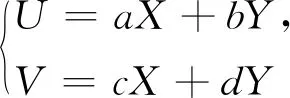
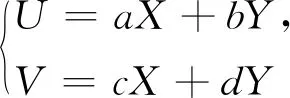
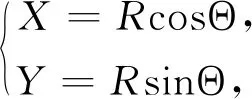
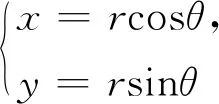
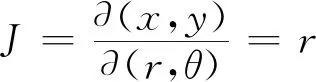
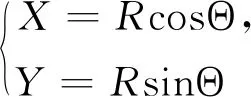
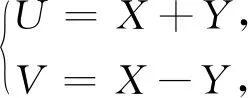
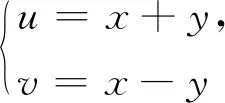
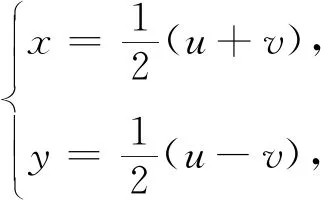

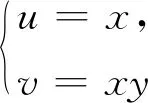
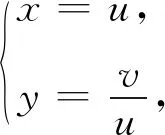

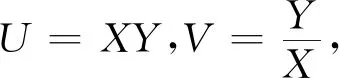
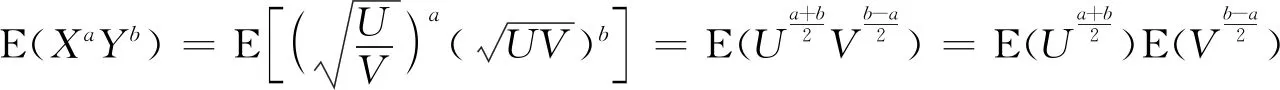
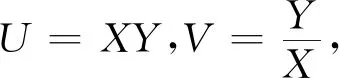
3 結(jié) 論

