安徽省南陵縣城東實(shí)驗(yàn)學(xué)校 鄒守文 (郵編:241300)

1 引言

Romanian Mathematical Magazine問(wèn)題1132(Proposed by Marin Chirciu-Romania)為:

在△ABC中,求證[1]:

(1)

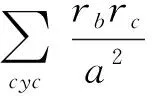
2 主要結(jié)果

定理1在△ABC中,有

(2)

(3)

定理2在△ABC中,有

(4)

(5)

3 定理的證明

3.1 定理1的證明

證明設(shè)△ABC的三邊長(zhǎng)為a,b,c,由(s-a)ra=(s-b)rb=(s-c)rc=sr,有

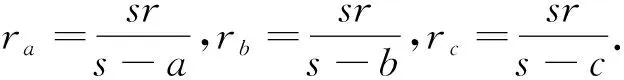
又由Gerretsen不等式s2≥16Rr-5r2,有

故(2)式成立.

又由Gerretsen不等式s2≤4R2+4Rr+3r2,有

故(3)式成立,從而定理1得證.

3.2 定理2的證明

在[2]中,已證得

(6)

由(3)(5)式,有

故(4)式成立.

因?yàn)?/p>

結(jié)合(2)式,有

故(5)式成立,從而定理2得證.

3 結(jié)論的討論

綜合(2)(3)式,有:

(7)

聯(lián)合(4)(5)式,得到一個(gè)不等式:

(8)

除此之外,還能夠得到一個(gè)恒等式:

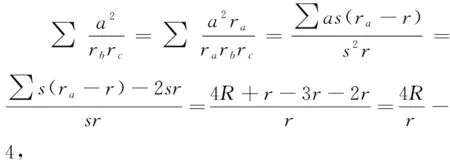
(9)