Zhuoqun Zheng(鄭卓群), Han Li(李晗), Zhu Su(宿柱), Nan Ding(丁楠), Xu Xu(徐旭),

Haifei Zhan(占海飛)4,5,?, and Lifeng Wang(王立峰)1

1State Key Laboratory of Mechanics and Control for Aerospace Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

2School of Management Science and Information Engineering,Jilin University of Finance and Economics,Changchun 130117,China

3College of Mathematics,Jilin University,Changchun 130012,China

4College of Civil Engineering and Architecture,Zhejiang University,Hangzhou 310058,China

5School of Mechanical,Medical and Process Engineering,Queensland University of Technology,Brisbane 4001,Australia

Keywords: carbon nanothread,size effect,natural frequency,modal shapes,molecular dynamics simulation

1.Introduction

Due to their excellent physical and chemical properties,[1]low-dimensional carbon nanostructures are ideal materials for a broad range of applications, such as nanoscale resonator-based nanoelectromechanical systems,[2,3]flexible electronics,[4]and next generation devices.[5]Carbon possesses innumerable allotropes due to its different hybridization states,including sp1,sp2,and sp3bonds as well as their combination.In past decades, the sp2bonded carbon nanostructures, such as carbon nanotubes (one-dimensional, 1D) and graphene (two-dimensional, 2D), have received huge intensive interests from academic and engineering communities.Thanks to the recent successful synthesis of carbon nanothreads (1D)[6,7]and diamane (2D),[8]the sp3bonded carbon nanostructures are receiving an increasing research focus.

Compared to well-known sp2bonded carbon nanostructures,the novel sp3bonded carbon nanostructures have unique properties.For instance, the graphene layer has supreme inplane mechanical properties but hardly maintains a flat configuration in experiments.[9]However, recent successfully synthesized diamane has been predicted with excellent in-plane and out-of-plane mechanical properties,[10]which is a good candidate for nanoscale mechanical resonators.[11]Besides 2D structures,1D sp3bonded carbon nanothreads(NTH),recently synthesized through high-pressure solid-state reaction of benzene at room temperature,[6]are quite different from the carbon nanotubes(CNT).The CNT suffers from lateral flattening(or buckling),[12]while previous works report that mechanical properties of the NTH are tunable.[13–16]Unlike the CNT’s flat surface, NTH possesses a fully hydrogenated surface, which can be further functionalized without the introduction of additional defects.[17]It is known that functionalization is able to effectively improve the interfacial load transfer efficiency.Hence,due to the high interfacial load transfer efficiency,NTH and its functionalized structures are suitable for the applications as reinforcements for carbon nanofibers[18–20]and polymer nanocomposites.[21]

One of the differences of NTH from CNT is the diameter.It is reported that the diameter of NTH is less than 0.5 nm[22,23],while the diameter of CNT is usually larger than 0.5 nm.Such ultra-fine characteristic enables NTH to have encouraging applications, such as nanoscale mechanical resonators for mass sensing.It is reported that NTHs demonstrate an extreme mass resolution (～0.58 yg) which is almost one order of magnitude higher than that of CNTs (～10 yg), and a high quality factor which is generally two times than that of CNTs.[24]These intriguing features suggest that NTHs could be highly attractive candidates for high performance nanoscale mechanical resonators.However, the ultra-fine characteristic of NTHs may introduce the size effect,which could influence NTHs’transverse vibrations.Therefore,before designing and fabricating the NTH-based nanoscale mechanical resonators,it is necessary to comprehensively understand the transverse vibration characteristics of NTHs.

From a theoretical perspective,several theories are available for describing the size effect of nanomaterials, including nonlocal theory[25]and modified couple stress theory(MCST).[26]There have been lots of previous works[27–30]focusing on theoretical modeling of micro/nano-beams considering the size effects.However,all these theories contain scale parameters, which are usually related to the materials.These parameters are hardly obtained from experiments, especially for such novel materials.Molecular dynamics simulation is a powerful tool for calibration of the scale parameter.[31,32]To this end, this work aims to investigate the transverse vibrational properties of ultra-fine NTHs through large-scale molecular dynamics (MD) simulations.MCST-based Timoshenko beam model is utilized to describe the size effect of NTHs’free vibrations.The length scale parameterlof MCST is calibrated based on the MD simulation results.Furthermore, it is found that the MCST has a limited influence on the modal shapes.

2.Methodology

2.1.Atomistic simulation

Figure 1(a) shows the structure of the NTH considered in this work.Compared with other topologically distinct NTHs,[33]the tube(3,0)NTHs contain a relatively regular and uniform structure.The simple and consistent state of the tube(3,0)NTH makes its vibrational properties free from the influences originating from topological factors,such as asymmetric cross-sectional shape and pre-strain.Hence, it is suitable for the study focusing on the size effect of ultrafine structures.

To acquire its free vibration characteristics, a series of MD simulations have been performed.In these simulations, the widely used adaptive intermolecular reactive empirical bond order (AIREBO) potential was employed to describe the C–C and C–H atomic interactions of the NTH.[34,35]Recent works showed that this potential can well reproduce or predict the mechanical properties of different carbon nanostructures,[36–38]including the NTH.[39–41]To avoid the spurious high stress at potential high bond strain, the cut-off distance of the AIREBO potential was chosen as 2.0 ?A.[42–44]The NTH sample was first optimized by the conjugate gradient minimization method.[45]Then, initial settings were applied.As shown in Fig.1(a),in order to mimic the clamped–clamped(CC)beam,the two ends(two unit cells each)of the NTH were fixed.While one end was fixed and the other one remained free for the cantilever (clamped—free, CF) beam.The initial temperature of the moving part was set to 10 K.The relatively low temperature was used to eliminate the influence of thermal fluctuations on the vibration behaviors of NTHs.After that,the free vibration of the NTH was actuated.Since the velocity excitation and the displacement excitation have the same effect in inducing free vibrations,[46]a sinusoidal velocity excitationv(x) along NTH’s length direction was applied.To actuate different vibration modes, excitation functions similar to corresponding vibration modes were used as illustrated in Fig.1(b),

where,A0is the actuation amplitude,kis the order of vibration mode,andLis the effective length of the NTH which excludes the fixed edges.A convergence study had been conducted on the magnitude of the actuation amplitudeA0(see supporting information S1 for details).In order to avoid the introduction of geometric nonlinearity and large thermal fluctuations,A0was chosen as 0.1 ?A/ps.In this study, the first four modes of free vibration were considered.So,kwas chosen to be 1, 2,3 and 4,respectively.The NTH sample was oscillating freely under an energy conserving(NVE)ensemble for 4 ns.

Fig.1.(a) Schematic view of the NTH sample with different boundary conditions, (b) the profile of the initial actuations for different vibration modes and boundary conditions.

For obtaining basic mechanical parameters of tube (3,0)NTHs, tensile and torsional tests were performed by applying the MD simulations.In this part, an NTH sample with the length of 7.56 nm was tested under a canonical ensemble(NVT)by using a Nosé–Hoover thermostat.[45,47]For tensile tests, the sample was stretched under a low strain rate of 10-7fs-1.And for torsional tests,the sample was twisted under a low rotation rate of 3×10-7rad·fs-1.The tensile or torsional load was applied to one end of the sample, with the other end being fixed.

A small timestep of 0.5 fs was used for all simulations,and non-periodic boundary conditions for the simulation box were applied in all directions.All simulations were performed by using the open-source large-scale atomic/molecular massively parallel simulator(LAMMPS)code.[48]

2.2.Classical beam theories

Based on the previous studies of tube (3,0) NTHs, the persistence length is approximately 130 nm at 300 K.[14]In our studies, the maximum length of NTH is no more than 30 nm,which means it can be treated as a beam.Meanwhile,the cross-section of the tube(3,0)NTH is usually considered to be a circle with the diameterdof 0.5 nm,[14]as shown in Fig.1(a).Two classical beam theories,Euler–Bernoulli beam theory and Timoshenko beam theory,are utilized to investigate the NTHs’free vibration characteristics.

According to the classical Euler–Bernoulli beam theory,the governing partial differential equation is

whereEis the Young’s modulus,Iis the moment of inertia,ρis the density andAis the cross-sectional area.w(x,t) is the beam’s transverse displacement,xis position andtis time.For the classical Euler–Bernoulli beam,the rotational angleφequals to?w/?x.

For the classical Timoshenko beam theory,the governing partial differential equation is

whereGis the shear modulus,Kis the shear cross-sectional shape factor andφ(x,t)is the rotational angle.After eliminatingφin Eq.(3),the governing partial differential equation can be expressed as

Different boundary conditions are considered in free vibrations.The clamped–clamped boundary conditions are

The clamped–free boundary conditions are

By applying the above boundary conditions, characteristic equations of the Euler–Bernoulli beam and Timoshenko beam can be obtained respectively.However, these equations have no explicit expressions.Therefore,the natural frequencies and vibration modes are determined by numerically solving.

2.3.Theoretical models considering size effect

According to the MCST developed by Yanget al.,[26]the strain energy density for a linear isotropic elastic material is given by

whereσ,ε,χandmare the Cauchy stress,the classical strain and symmetric curvature tensors,and the deviatoric part of the couple stress tensor, respectively.The tensors are defined as follows:

wherei,j=1,2,3 represent thex,yandzdirections, respectively.uandθare displacements and rotation vectors.lis the material length scale parameter.λis the Lame’s parameter which is defined byλ=Eν/((1+ν)(1-2ν)),whereνis the Poisson’s ratio.

The motion equations of Timoshenko beam based on the MCST can be obtained as

The corresponding boundary conditions are

for clamped–clamped beams and

for clamped–free beams.

The modified Fourier series method combined with the penalty function method is utilized to numerically calculate the natural frequencies and corresponding vibration modes.[49,50]

3.Results and discussion

3.1.Calibration of mechanical parameters

For the purpose of investigating the transverse free vibration properties theoretically, basic mechanical parameters of NTHs including Young’s modulus, shear modulus and Poisson’s ratio are needed.Since NTHs’ static mechanical properties may be different from the bulk diamond due to the size effect caused by their ultrafine structures,MD simulations are used to determine these mechanical parameters.

Through the uniaxial tension of the NTH sample,Young’s modulus is extracted from the initial linear regime of the stress-strain curve.As illustrated in Fig.2(a), by fitting the data with the strain up to 2%, the tube (3,0) NTH shows the Young’s modulus of 1036 GPa, which is consistent with the known result (1089 GPa),[14]and the value of bulk diamond(1143 GPa).[51,52]The Poisson’s ratio is also calculated based on the uniaxial tension simulation,which is defined as the ratio of diameter change to length change.Figure 2(b) shows the MD results of Poisson’s ratio with the strain from 1% to 2%, which vary considerably between-0.15 and 0.2.Such fluctuation may be resulted from the irregular cross-sectional shape of this ultrathin structure and the thermal fluctuation of the simulation.By averaging these values,the Poisson’s ratio is calculated to be 0.03,which agrees with the Poisson’s ratio of bulk diamond(≈0.07[51,52]).

Fig.2.Tensile tests of the NTH sample.(a)Tensile stress as a function of strain.The red point shows the stress when the sample is under 2%strain.The black line is the fitted line based on the data with the strain up to 2%.(b)Poisson’s ratio with the strain from 1%to 2%.

Torsional tests are applied to the sample to gain its shear modulus.The torque-angle data are shown in Fig.3(a).It is clear to see the torque-angle data experience relatively large fluctuations,which may be caused by temperature.The torque-angle curve can be fitted to a functionT=GIpθ/L,whereIpis the polar moment of inertia.The shear modulus is calculated to be 199 (±7) GPa.To ensure the correctness of the calculation, strain energy is also utilized to determine the shear modulus.Figure 3(b) reveals the data of strain energy changing with the twisted angle.Similarly, the strain energy varies largely.By fitting the strain energy data to a functionVε=GIpθ2/2L,the shear modulus is determined as 195 (±12) GPa, which is consistent with the above result.However,this is quite different from the value of bulk diamond(537.9 GPa[53]and 535 GPa[51]).We suppose that such difference may be related to its ultrafine structure,the surface effect and geometric assumptions of its cross section.In all, an averaged shear modulus of 197 GPa is adopted for the following calculation.

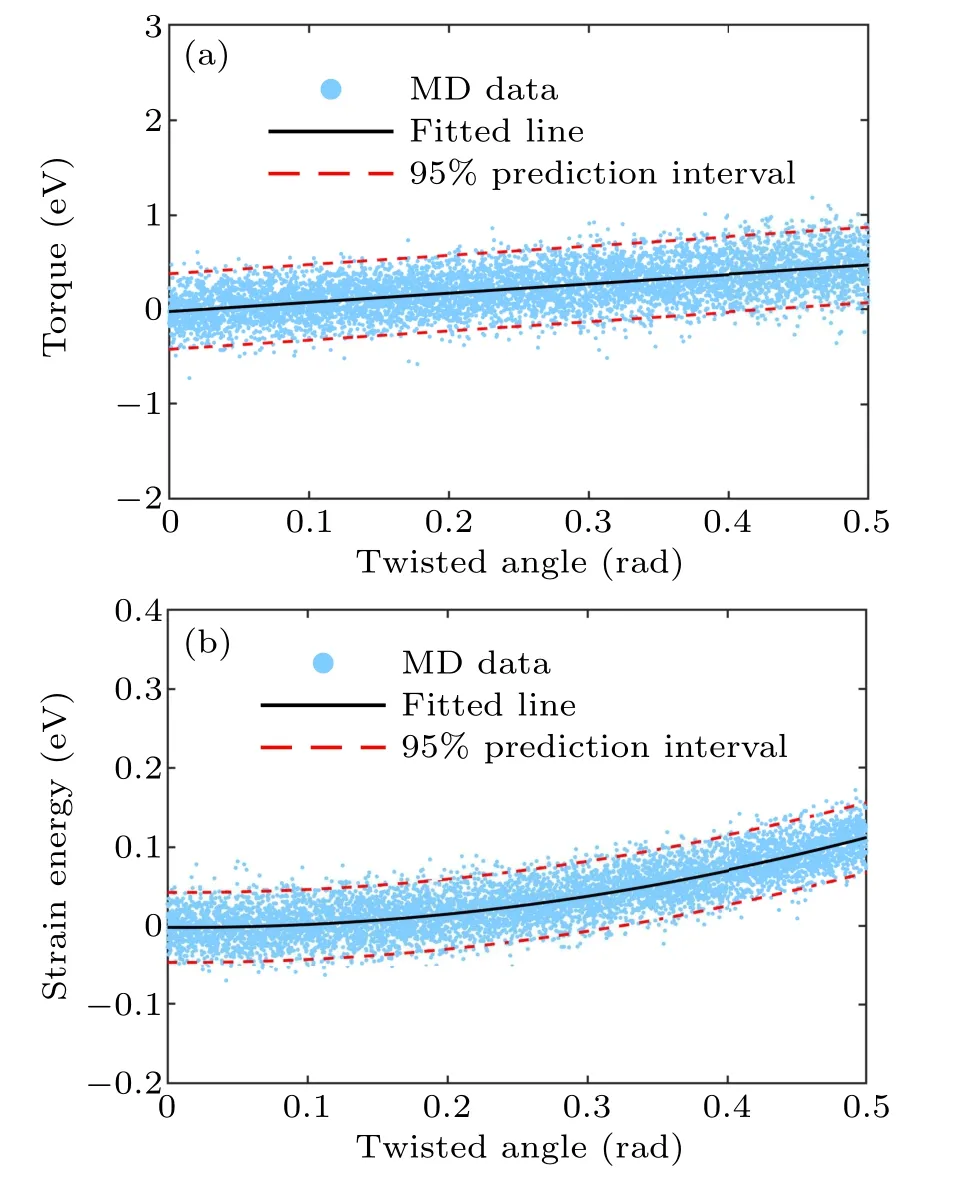
Fig.3.Torsional tests of the NTH sample.(a)Torque vs.twisted angle.(b) Strain energy vs.twisted angle.The black lines are the fitted lines based on the data with the angle up to 0.5.

3.2.Size effect in free vibrations

From MD simulations of transverse free vibrations,time history of center of mass of the NTH can be obtained.By applying the fast Fourier transform (FFT) on the trajectory of certain parts, the frequencies of corresponding vibration modes can be determined.Figures 4(a)–4(d) present the 1st to 4th order frequencies under the clamped–clamped boundary constraint in black dots.With above mechanical parameters, the frequencies of classical beam theories are also depicted in Figs.4(a)–4(d).In order to analyze the difference between the results of MD simulations and classical theories,the difference is defined as Diff=(ftheory-fMD)/fMD.Figure 4(e) shows the difference of first four order frequencies.It is found that the frequencies of Euler–Bernoulli beam are larger than those of MD simulations,while the frequencies of Timoshenko beam are smaller than those of MD simulations,especially when the sample length is small.The clamped–free boundary constraint is also considered (see supporting information S2).Similar phenomena are found when the NTHs are under the clamped–free boundary constraint.

With the decrease of the slenderness ratio, especially when the value is smaller than 20,the differences between the results of MD simulations and classical theories(both Euler–Bernoulli beam and Timoshenko beam)become larger.Similar phenomena can be found in clamped–free NTHs(see supporting information Fig.S2 for detailed results).It seems that size effect exists in transverse free vibrations of NTHs.For Euler–Bernoulli beam theory,it is known that shear deformation and moment of inertia are not considered,which might be one of the reasons for the difference in frequencies.However,the difference in the Timoshenko beam cannot be explained by a similar perspective.Hence,these results indicate the existence of the size effect.

Recall Subsection 3.1,the Young’s modulus,shear modulus and Poisson’s ratio of NTHs are all from MD simulations.In other words,the mechanical parameters used in the calculations of classical theories represent the static elastic properties of NTHs at this scale.Therefore, in order to capture the size effect shown in transverse free vibrations of NTHs, classical beam theories need to be modified.Scale parameters are introduced to refine the classical beam theories, such as nonlocal theory and MCST.The literature[54]suggests that nonlocal theory can account for the softening stiffness of nanobeam and MCST can induce the stiffness-hardening effect.Based on above results, the Timoshenko beam with MCST is investigated in following sections.

3.3.Calibration of the scale parameter

As illustrated in Subsection 2.3, MCST contains a scale parameterl,which is dependent on materials.However,to the best of our knowledge,there are no direct reports for the scale parameters of such novel ultrafine NTHs.In order to apply the MCST-based Timoshenko beam theory for the transverse vibration analysis of NTHs,it is necessary to provide the value of scale parameterl.The scale parameters in the range from 0 nm to 0.3 nm are investigated.

Fig.5.Variation of frequencies of clamped–clamped NTHs predicted by MCST with respect to 1/L2 and length scale parameter l: (a) first order mode,(b)second order mode,(c)third order mode,and(d)fourth order mode.The black points show the results of atomistic simulations.

In Fig.5, variation of the 1st to 4th order frequencies based on MCST under clamped–clamped boundary condition is depicted with respect to 1/L2for different values ofl.From the curves with different length scale parameterl,it is seen that MD simulation results are close to the results ofl=0.1 nm.In order to obtain a more accuratel,the values of 0.05 nm,0.1 nm and 0.15 nm are considered.Table 1 presents the detailed data of the first four order frequencies of NTHs with slenderness ratio smaller than 20 and the corresponding absolute value of differences.Based on the average differences of the 1st to 4th order frequencies,the length scale parameterlis estimated as 0.1 nm.

Free vibrations of the NTHs under clamped–free boundary condition are also investigated for the calibration of length scale parameterl.Similar trends can be found in these cases (see supporting information Fig.S3 and Table S1 for detailed results).These results indicate that the length scale parameterlis estimated as 0.1 nm.It is consistent with the above results.

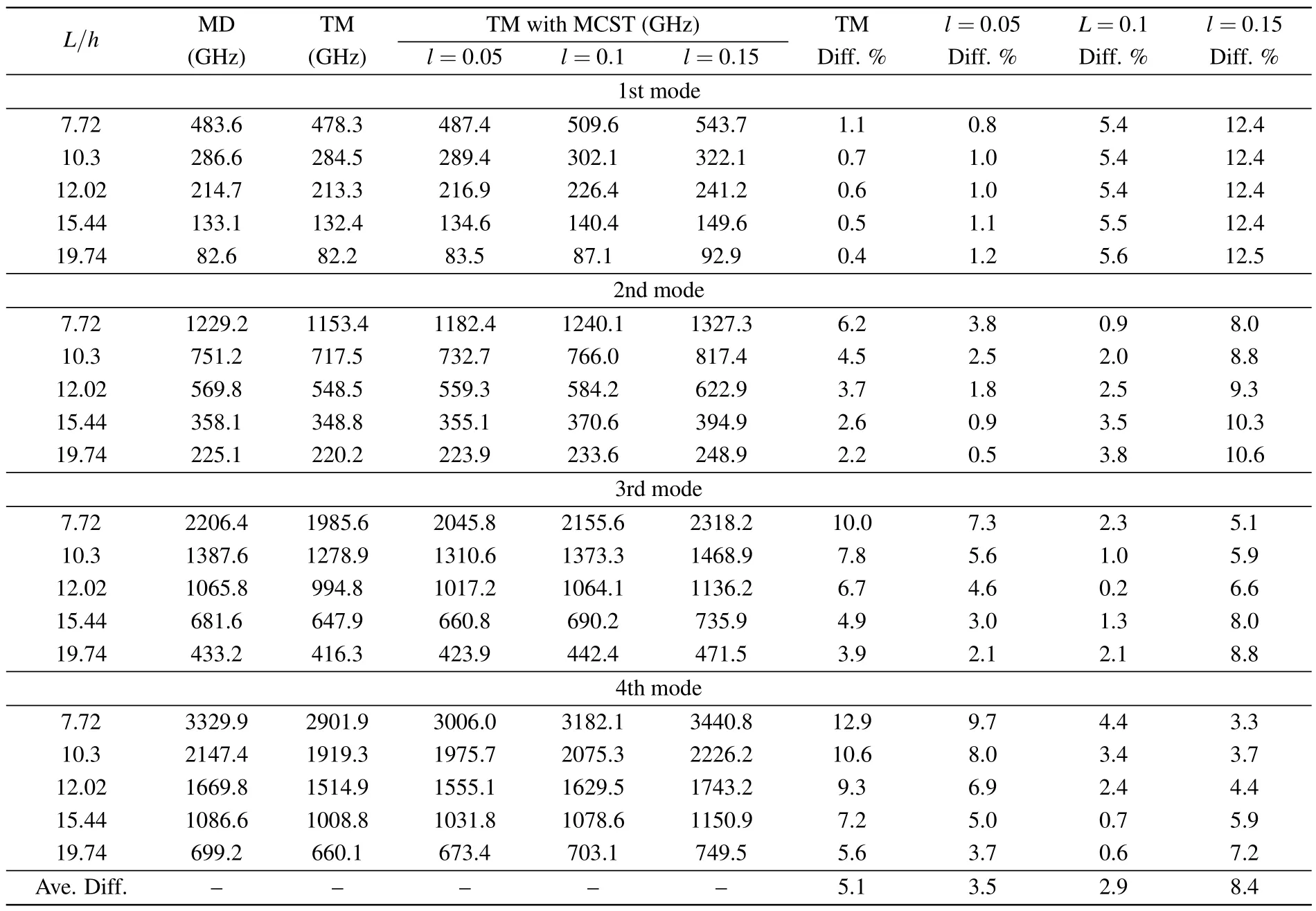
Table 1.Frequencies of the NTH under clamped–clamped boundary constraint.

3.4.Modal shapes

Subsequently,the first four order modal shapes of NTHs’vibrations are studied.Since the length scale parameterlin MCST plays an important role in the analysis of short NTHs(with relatively small slenderness ratio),a 5.15-nm-long clamped–clamped NTH is chosen.

In Fig.6, the modal shapes obtained by MD simulations are shown in black points, while the modal shapes calculated by MCST-based Timoshenko beam theory are presented in different lines dependent on the different values ofl.From the left panel of Fig.6, it is seen that the lines almost overlap with each other and basically agree with MD results.It seems that the introduction of MCST has little effect on the modal shapes.However, by zooming in the modal shapes of NTHs’ends in the right panel of Fig.6,it is interesting to note that the modal shapes calculated by MCST-based Timoshenko beam theory are closer to those obtained by MD simulations with the increase ofl.It is due to the different clamped–clamped boundary conditions between classical Timoshenko beam and MCST-based Timoshenko beam.By comparing Eqs.(5) and (10), it is found that the introduction of MCST brings?w/?x(0)=0 and?w/?x(L)=0 into the boundary conditions.With the constraint of the first derivative of transverse displacement, the curves of MCST-based Timoshenko beam tend to flat when they are close to the ends.Therefore, the introduction of MCST mainly affects the clamped–clamped boundary conditions and makes the modal shapes a little closer to those of MD results.

Modal shapes of the NTHs under clamped–free boundary condition are also investigated (see supporting information Fig.S4 for detailed results).It is found the modal shapes from theory calculation have a deviation from those obtained by MD simulations.Such deviation may be resulted from the one-end-free boundary condition.For the atomic model, it is known that the edge effect occurs at the free end of NTH.Both classical and MCST-based Timoshenko beam theories cannot capture the edge effect.Therefore, there is a deviation in the modal shapes between theories and MD simulations.Nevertheless, the introduction of MCST still can make the modal shapes a little closer to those of MD results.

Fig.6.Variation of modal shapes of the 5.15-nm-long clamped–clamped NTH predicted by MCST with respect to length scale parameter l: (a)first mode, (b) second mode, (c) third mode, and (d) fourth mode.The black points show the results of atomistic simulations.The right panels are the enlarged figures of the red boxes on the left.

4.Conclusion

Based on a series of large-scale molecular dynamics simulations, we study the transverse free vibrations of the ultrafine carbon nanothreads targeting the NTH-based nanoscale mechanical resonators.By taking the tube(3,0)NTH as representative structure,different boundary conditions,including the clamped–clamped and clamped–free constraints, are considered.Size effect is found in the transverse free vibrations of NTHs.From a theoretical perspective,the MCST-based Timoshenko beam theory is utilized for describing the size effect in free vibrations of the ultrafine NTHs.The results show that it is appropriate to choose 0.1 nm as the length scale parameterl.Furthermore,for the modal shapes of the first four order vibrations, it is found that the introduction of MCST makes the modal shapes at the clamped boundary a little closer to those of MD results.Overall,it is revealed that to some extent the MCST-based Timoshenko beam theory can well describe the transverse vibration characteristics of the ultrafine NTHs,which shed light on the design and fabrication of the NTHbased nanoscale mechanical resonators.

Acknowledgments

Project partially supported by the National Natural Science Foundation of China (Grant No.12102176), the China Postdoctoral Science Foundation (Grant No.2022M711617),and the Natural Science Foundation of Jiangsu Province of China (Grant No.BK20210274).Partially supported by the High Performance Computing Platform of Nanjing University of Aeronautics and Astronautics.