Li-Na Luan(欒麗娜), Mei-Yu Zhang(張鎂玉), and Lin-Cheng Wang(王林成)

School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords: Floquet dynamical quantum phase transitions,periodic kick,XY spin chains

1.Introduction

Quantum phase transitions(QPTs)have attracted a great deal of attention for decades.Different from traditional phase transitions,QPTs are solely driven by quantum fluctuations,[1]and in the context of quantum information theory,[2]such quantum phenomena have been deeply investigated and many essential properties have been revealed.[3–5]In recent years,dynamical quantum phase transitions (DQPTs), which have gained much attention as an extended study of QPTs to the non-equilibrium case, have been theoretically investigated in different physical dimensions, and huge progress has been provoked by the experimental observations,[6–21]for example, quenching dynamics between different Floquet topological phases is simulated by quantum walking dynamics,where DQPTs and underlying dynamical topological order parameters (DTOPs) are characterized by interference-based measurement experiments.[10]DQPTs concern the nonanalytic behaviors in many-body systems after a sudden change of the parameters,so-called quantum quench,[11]and appear whenever the time evolved state becomes orthogonal to the initial state,which are often measured by the Fisher zeros in the context of Loschmidt amplitudes.[12,22–24]Furthermore, DQPTs have also been extended to reveal the changes of topological invariants for quenched topological quantum systems.[25–27]

The Floquet theory serves as a highly controllable and versatile tool in quantum control,and has revealed many nontrivial effects in periodic driven quantum systems,[28–38]especially the topological quantum system.[29–31,35,38–45]Floquet DQPTs, which exhibit exotic new properties in many nonequilibrium quantum many-body systems beyond quenches,have been proposed in time periodically driven Floquet quantum systems.[18]Different from conventional DQPTs usually observable only in transient time scales,the non-analytic cusps in the return rate of Floquet DQPTs are found to recur periodically in time with a non-decaying global profile.[46–50]As an extended research area of DQPTs, richer non-equilibrium phases and intrinsic features have been revealed in timeperiodic driven quantum systems and experimentally verified for Floquet DQPTs, and the related problems have become one of the most attractive areas of developing nonequilibrium research topics.Research of Floquet DQPTs has been extended to various quantum systems, such as the spin chain model,[47,49]synchronized periodic driving systems,[51]dissipative systems,[52]periodically driven topological systems,[53,54]and periodic quenching topological systems.[50]Many non-equilibrium phases have been revealed in time-periodic driven quantum systems and experimentally verified.[18,44–46,54]

In order to deeply understand the essential nature of Floquet DQPTs, some exactly solvable periodically timedependent models have also been proposed, and it has been shown that,when a periodical driven system is initialized in a periodic quenched Floquet topological phase,the Floquet system can also show topologically nontrivial signatures.[50]As we know,δ-function periodic kicking is another special periodic driving and may provide an interesting analytical solvable model, which may also change the system and induce new phenomena,for instance,periodic behavior may result in a new phase diagram in a topological system,changes the critical point of the quantum phase transition, etc.[55–58]It is an interesting topic to consider effect of periodic kickings in Floquet systems with DQPTs.

The exactly solvable transverseXYspin chain[59]has been widely used to investigate quantum phase transitions by many kinds of perspectives from quantum information theory,[60–71]such as the Loschmidt echo,[72]ground state fidelity,[73]quantum entanglement,[74,75]and geometric phase.[76–80]TheXYspin chain model has also been experimentally realized and studied, such as the relation between geometric phase and the ground state quantum phase transitions,[81]the geometric phase of the ground state of the three-self-spinXYmodel using nuclear magnetic resonance(NMR) technology.[82]A periodically drivenXYspin chain has been proposed as an analytically solvable model to study changes of quantum phase transitions.Floquet DQPTs of pure and mixed states in an extendedXYmodel driven periodically by a staggered magnetic field are also investigated.[47]Motivated by the above studies, in this paper we propose an analytically solvable periodic driven model, which consists of the usual transverseXYspin chain under periodic kicking, to study the Floquet DQPTs emerging in such a system.The critical properties and phase diagram of the model will be changed by the periodic kicking,by both the kicking strength and kicking period.For each micromotion of the periodic driven, we will show that the Floquet DQPTs will appear, which can be verified by the Loschmidt echo, the geometric phase, or even the dynamical topological order parameter.It is a simple and analytically solvable Floquet system and we believe that the Floquet DQPTs in the periodic kicking systems are also valuable used to reveal the essential mechanism of the intrinsic features of Floquet DQPTs.

The remainder of the paper is arranged as follows.In Section 2,we introduce the exact solution of the Floquet effective Hamiltonian of the periodically kickedXYspin chain.In Section 3, we study the Floquet DQPTs emerging in the micromotion of the Floquet dynamics,by considering the eigenstate and the ground state of the effective system as initial states respectively,and discuss the Floquet DQPTs of the system from different physical quantities characterization.Finally,we summarize our study in Section 4.

2.Transverse XY spin chains under periodic kickings

In this section,we briefly give the solution of our model.Consider the transverseXYspin chain under the periodic kicking,whose Hamiltonian can be expressed as

whereH0is the Hamiltonian for originalXYspin chains,i.e.,

andH1(t) is the driving Hamiltonian, which consists of periodic kicking alongz-direction,

In the above expressions,are the usual Pauli operators atl-site in the chain;λandγare the strength of the transverse field and the anisotropy parameter of theXYcoupling;αis the kicking strength; andTis the driving period.We will always consider the periodic boundary condition for our system.

The Hamiltonian of the transverseXYspin chainH(t)can be mapped to a quasi-Fermion system by the Jordan–Wigner transformation,

and by the discrete Fourier transformation in the case of periodic boundary condition,

one can obtain the quasi-Fermion form Hamiltonian

where the kernel Hamiltonian ishk(t)=h0,k+h1,k(t), which is defined as

Assume that theδ-pulses kick is added at momentT1for each period,then each period of time will be divided into two parts by the kick,T=T1+T2.However,different evolutions of the state can always be obtained by a unitary transformation,i.e.,

where we have defined two forms of the unitary-transformequivalent effective Hamiltonian, i.e., ～heff,kis the effective Hamiltonian defined by assuming theδ-kick added at the end of each period,while the effective Hamiltonianheff,kis defined for a general case of the kicking time.The above unitary operator determines the dynamics at timet=nT,n=0,1,2,...of the system.For many more periods, the system will only obtain an extra phase factor exp(-iheff,knT).

Using the definition (9) for the effective Hamiltonian by one period of evolution,we can analytically obtain ～heff,kas

where we have defined

and

Then, the effective Hamiltonianheff,k=ξkσ·nkwithnk=(nk,x,nk,y,nk,z)will have the same eigenvalues with ～heff,k,andnkreads

One can easily verify that,in the case ofα=0 andT2=0,the above effective Hamiltonian can be simplified to the originalXYspin-chain HamiltonianH0.

The kicking strengthαand kicking periodTwill change the effective Hamiltonian of the system,and different time intervals of the periodicδ-kick added on the system will result in different micro-motions, giving possible chances for the Floquet DQPTs in each period of time evolution.In the present study, we only consider one periodic micromotion during the stationary evolution of the system,i.e,the initial state for each period keeps the same,except for a phase factor.

Assume that the initial state for each period is|ψk(0)〉and the periodicδ-kicks are added during arbitrary timeT1in every period,i.e.,each period of evolution have been divided into two parts,0＜t ＜T1andT1＜t ＜T,(T=T1+T2),then the evolution of the system in one period can be expressed as|ψk(t)〉=Uk(t)|ψk(0)〉,with the time-dependent evolution operator defined as

3.Floquet DQPTs in the periodically kicked XY spin chain

In this section, we consider the eigenstate as well as the ground state of the effective Hamiltonian as the initial state of the system, which ensures the same evolution for each period except a phase factor,and we show that multiple Floquet DQPTs can emerge in the micromotion for each period of the Floquet dynamics.Some physical quantities have been used to characterize the Floquet DQPTs in the periodically kickedXY-spin system,e.g.,the rate function of return amplitude,the Pancharatnam geometric phase and the dynamical topological order parameter have been calculated, and these concepts are briefly introduced in Appendix.

3.1.Eigenstate as the initial state

Consider that the initial state for each period of the Floquet system is given by the eigenstate|χ±,k〉 of the effective Hamiltonian,i.e.,

which satisfies

or equallyheff,k|χ±,k〉=±ξk|χ±,k〉,then the state for any momentumkcan also be obtained as

By Eq.(15), we can obtain the return amplitude (see Eq.(A1)in Appendix),i.e.,

for 0＜t ＜T1,and

forT1＜t ＜T.We numerically simulate the quantum phase transition properties of the periodic kicking on the spin chain from the two aspects of the kicking strength and time.In the case ofGk(t)=0,both the real part and imaginary part should be zero,which will result in the following condition:

for 0＜t ＜T1,and

forT1＜t ＜T.The equations can be used to determine the critical momentumkcand the corresponding critical timetc.

Fig.1.The return amplitude |Gk(t)| of the system for momenta k ∈(-π,π), λ =0.5, t ∈(0,2π), T1 =π and T =2π: (a) γ =0.15, (b)γ =1.

Fig.2.[(a)–(d)] The return amplitude |Gk(t)| of the system for momenta k ∈(-π,π), γ =1, λ =0.5, α =1.5π and T =2π: (a)T1/T =0.1, (b) T1/T =0.4, (c) T1/T =0.6, (d) T1/T =0.9.[(e)–(h)] The rate function of return amplitude f(t) with the kicking time for one period T ∈(0,2π): (e)T1/T =0.1,(f)T1/T =0.4,(g)T1/T =0.6,(h)T1/T =0.9.The black dotted line represents the boundary line of the periodic kicking time t=T1/T.

The anisotropy parameterγcharacterizes the transformation from the Ising chain to theXXspin chain of the system,and it may affect the properties of the Floquet DQPTs.Figure 1 shows the numerical results of the return amplitude versus the kicking strength, where we have setα ∈(0,2π) andT1/T=0.5.From the above analytical expressions and the numerical simulations,we can clearly find that with the increasingγ ∈(0,1], more zero points appear, and the DQPTs may appear several times with the kicking strength varies.Thus,a feasible strategy for researching richer Floquet DQPTs can be provided by the anisotropy of the spin chain.

Theδ-kicks may be added at arbitrary moment in each period, which will result in different regular patterns of Floquet DQPTs.Figures 2(a)–2(d) shows the return amplitude|Gk(t)|withγ=1,λ=0.5 and different ratios ofT1toT2.We can find that theδ-function kick added in each period may hinder or postpone the emergence of the Floquet DQPTs points.Figures 2(a)–2(d) also show a clear regularity of symmetry with time distribution of the two stagesT1andT2before or after the kick.

The explicit expression of the return rate functionf(t)(see Appendix) of the periodical kicking system can be obtained by definition

in the case of 0＜t ＜T1,and

in the case ofT1＜t ＜T.

Figures 2(e)–2(h)show the rate functionf(t)with different kicking times forT1/T=0.1,0.4,0.6,0.9,where we have sett ∈(0,2π),γ=1,λ=0.5, andT=2πin the calculation.The rate functionf(t) consistently shows the mutation inflection points with the return amplitude|Gk(t)|.In each period,mutation inflection points will emerge if the time distribution is long enough before or after the kick, which indicates the same principle for the emergence of Floquet DQPTs.In the thermodynamic limit,the rate function of return amplitude(A1),and its time derivative becomes a non-analytic time function at the critical time, and the rate function graphs are consistent with the return amplitude shown in Figs.2(a)–2(d),respectively.The mutation inflection points off(t) more intuitively reflect the critical time of Floquet DQPTs,which are consistent with the former results.Figures 2(e)–2(h)can also capture the regularity of symmetry with time distribution of the two stagesT1andT2before or after the kick.

The Floquet DQPTs of the system can also be characterized by the Pancharatnam geometric phase (see Eq.(A3) in Appendix),and the geometric phase of the system can be expressed in detail as

in the case of 0＜t ＜T1,the first stage before kicking,and

in the case ofT1＜t ＜T,the second stage after kicking.

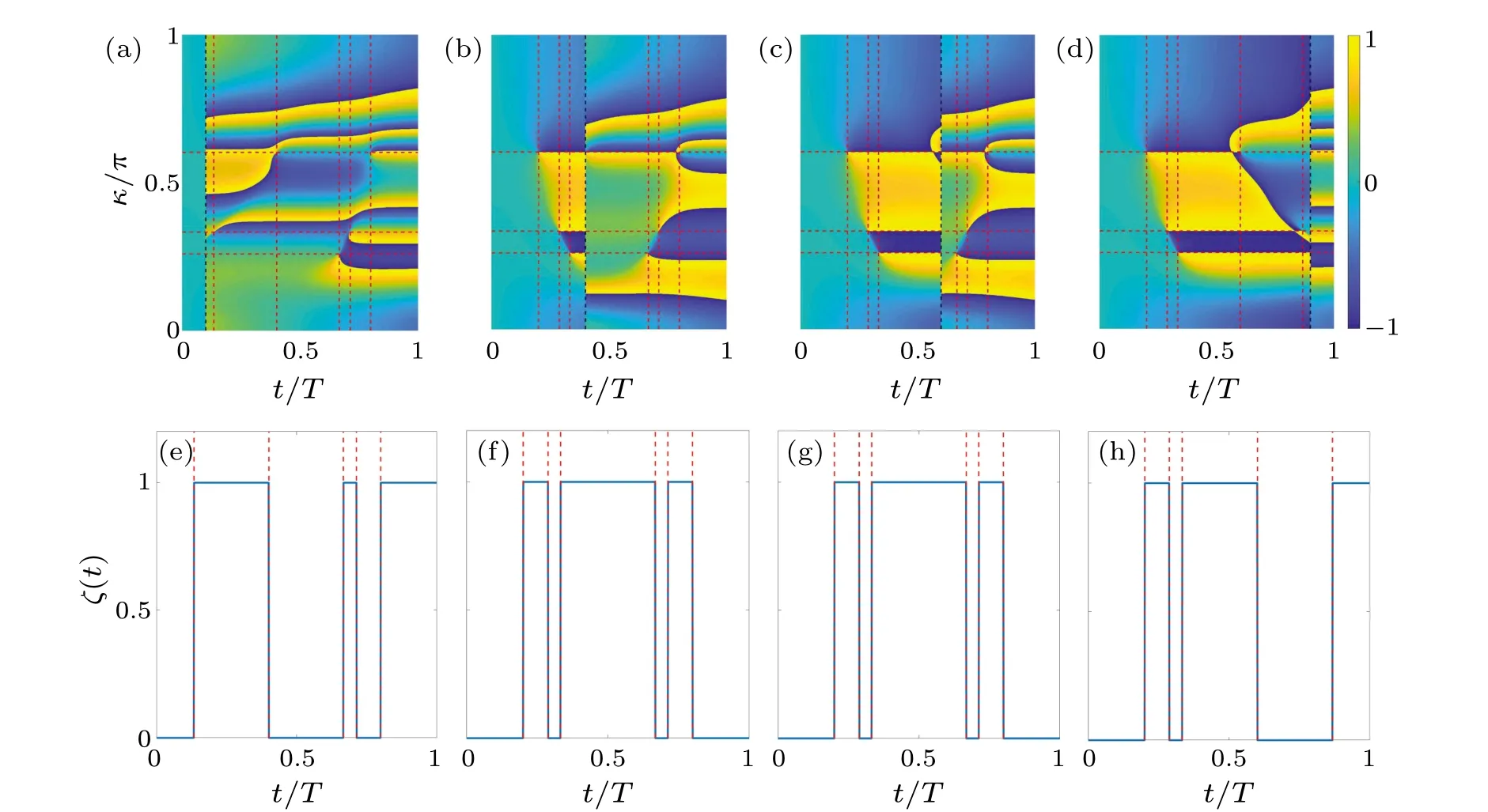
Fig.3.[(a)–(d)]The Pancharatnam geometric phases (t)with different kicking time distributions for fixed period T ∈(0,2π):(a) T1/T =0.1, (b) T1/T =0.4, (c) T1/T =0.6, (d) T1/T =0.9.[(e)–(h)] The order parameter ζ(t) with different kicking time distributions for fixed period T ∈(0,2π): (e) T1/T =0.1, (f) T1/T =0.4, (g) T1/T =0.6, (h) T1/T =0.9.Other parameters of all pictures are set as γ =1,λ =0.5,α =1.5π,and T =2π.The black dotted line represents the boundary line t=T1/T that separates the two kicking periods,and the red dotted line represents the the critical time tc of Floquet DQPTs.

Figure 3 shows the geometric phase for one period of the periodically kicked system,γ=1,λ=0.5.We have also set the parameters of all figures asT=2π, and setT1/T=0.1,0.4, 0.6, 0.9 for Figs.3(a)–3(d), respectively.For each figure, the intersection of the horizontal red dashed line and the vertical axis corresponds to the critical momentumkc,and the intersection of the vertical red dashed line and the horizontal axis represents the critical timetc.We have set(t)in the range from-πtoπ, neglecting the difference of 2πfor the geometric phase.The Floquet DQPTs have been captured by the geometric phase, showing a jump from-πtoπfor a periodT ∈(0,2π).It clearly shows that the critical time for the system to present Floquet DQPTs is consistent with the previously studiedGk(t)andf(t).

The dynamical topological order parameterζ(t)with different kicking time distributions for fixed periodT ∈(0,2π),γ=1,λ=0.5 have also been shown in Fig.3.The parameters of these figures have been set asT=2π,andT1/T=0.1,0.4,0.6,0.9 for Figs.3(e)–3(h),respectively.The dynamical topological order parameterζ(t)exhibits a perfect quantization as a function of time between changing times of two DQPTs.The change times are exactly corresponding to the critical points shown in Fig.2,which means that the abrupt jumps in the dynamic topological order parameterζ(t)consistently reflect the onset of Floquet DQPTs.In the absence of the Floquet topology, there is no direct correlation between Floquet DQPTs,fixed points,and dynamic topological order parameters,which are closely connected whenζ(t)=0, which indicate that the emergence of dynamic topological phenomena is protected by the Floquet topology.

3.2.Ground state as the initial state

Now, we consider that the initial state of the system is prepared as the ground state of the effective Hamiltonian,|ψk(0)〉=|Geff〉,which satisfies

and for each period,the analysis result of the return amplitude can be expressed as

According to Eqs.(8) and (14), one can obtain the analysis result ofG(t),

and for the conditionG(t) = 0, i.e., the DQPT appears at the time instances at which at least one factor becomes zero,whenever there is a modeksatisfying

In the case of 0＜t ＜T1,in order to find the Fisher zeros on the complex plane,one can extend ittoz=τ+it,which means

and thus we obtain

similarly,in the case ofT1＜t ＜T,one can obtain

Then, we will simulate the quantum phase transition properties of the periodic kick on the spin chain from the two aspects of the kicking strength and time.

Firstly, we consider the effect of the kicking strength to analyze the return amplitude of Floquet DQPTs.The returned amplitude of the system changes withαfor the driving periodT1/T=0.5,as shown in Fig.4,with the value range ofαbeing (0,2π).From the above exact calculations and the numerical simulations, we can conclude that the DQPTs appear as the kicking strength varies.This provides a feasible strategy for studying the DQPTs.

Figures 5(a)–5(d) show the numerical rate function, i.e.,Eqs.(32) and (33), where we have setγ=1,λ=0.5, andT1/T=0.1,0.4,0.6,0.9.The kick in each period can also hinder or postpone the emergence of the Floquet DQPTs points.The regularity of symmetry with time distribution of the two stagesT1andT2before or after the kick have also been shown in these figures.Several phase transition points may emerge in the rate functionf(t)for sufficiently long time of the stage separated by the kick.

The dynamical topological order parameterζ(t)can also display the Floquet DQPTs of the system,as shown in Fig.5,where we have setγ= 1,λ= 0.5 in the calculation.We have considered different kicking time distributions for the fixed periodT ∈(0,2π), and setT1/T= 0.1, 0.4, 0.6, 0.9 for Figs.5(e)–5(h), respectively.The rate function of return amplitudef(t), as well as the dynamic topological order parameterζ(t),consistently indicates the Floquet DQPTs points.The abrupt jumps in the dynamic topological order parameterζ(t) also correctly reflect the onset of Floquet DQPTs, indicating that the emergence of dynamic topological phenomena is also protected by the Floquet topology.

From the results of the former two examples,we can find that periodic kickings added on the spin chain system can also induce and detune the Floquet DQPTs,and different physical quantities can consistently characterize the emergence of Floquet DQPTs in the system.Since both the eigenstate and the ground state of the effective Hamiltonian as the initial state of evolution can ensure the same evolution for each period evolution of the system, our model may be used to predict the Floquet DQPTs of the system for some long time stable states of the periodically kicked systems.TheXYspin chain can be experimentally realized in many physics systems or simulated by simply systems, such as the nuclear magnetic resonance (NMR) technology,[81,82]the negatively charged nitrogen-vacancy center in diamond.[18]Our system may also be experimentally realized in such systems with extra periodic changedδ-pulse sequence kicking fields, the physical quantities such as geometric phase can be similarly measured.[18,81,82]

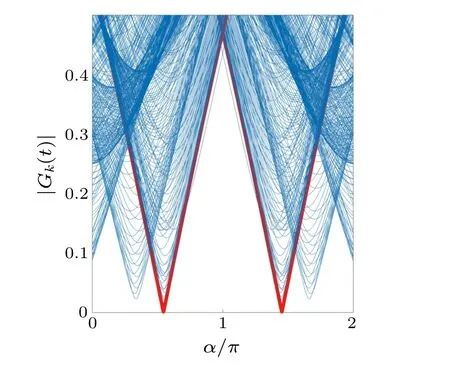
Fig.4.The returned amplitude |Gk(t)| of the system for momenta k ∈(-π,π), t ∈(0,2π).We have set γ =1, λ =0.5, T1 =π, and T =2π in the calculation.

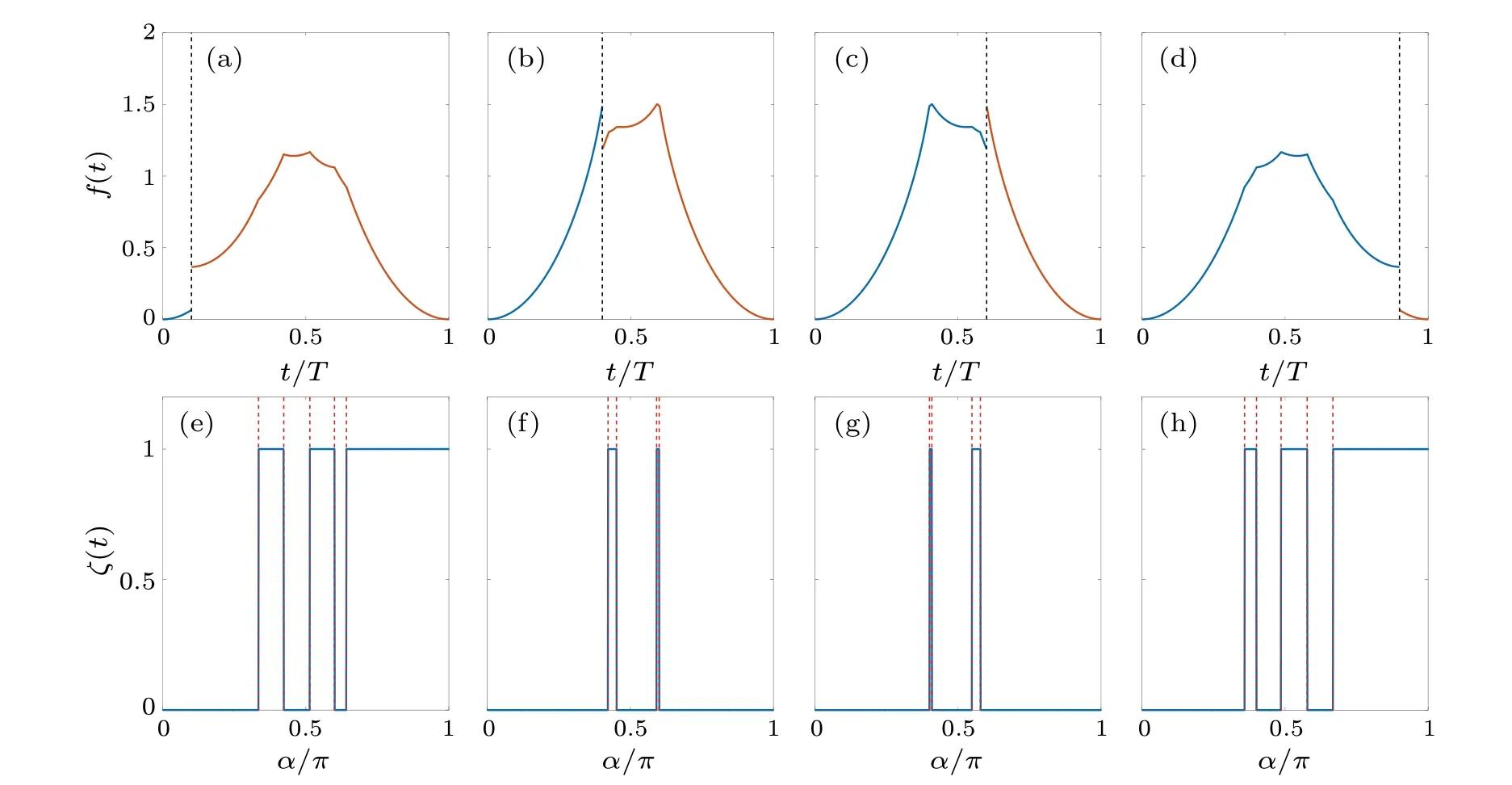
Fig.5.[(a)–(d)]The rate function f(t)of the system with momenta k ∈(-π,π)and period T =2π: (a)T1/T =0.1,(b)T1/T =0.4,(c)T1/T =0.6,(d)T1/T =0.9 in the calculation.(e)–(h)The order parameter ζ(t)with different kicking time distributions for fixed period T ∈(0,2π): (e)T1/T =0.1,(f)T1/T =0.4,(g)T1/T =0.6,(h)T1/T =0.9 in the calculation.Other parameters of all pictures are set as γ =1,λ =0.5,α =1.5π and T =2π.The black dotted line represents the boundary line of the periodic kicking time t=T1/T.

4.Conclusion

In summary, we have proposed and investigated a new analytically solvable model for Floquet DQPTs, i.e., the Floquet DQPTs of theXYspin chain under the periodic kicking drive.We obtain the exact expression of the Floquet effective Hamiltonian,and investigate the Floquet DQPTs emerging in the micromotion of the Floquet dynamics.By considering the eigenstate and the ground state of the effective Hamiltonian,we discuss the return amplitude,the rate function of the return amplitude,the geometric phase,and the dynamical topological order parameter of the system, and show that all these physical quantities consistently display critical points for each period of the Floquet DQPTs.The periodic kicking can induce a new phase diagram for theXYspin chain,and also induce the Floquet DQPTs of the system,where multiple FDQPTs within each driving period will be introduced,which are affected by tuning both the anisotropy of the spin chain and the kicking parameters.

To effectively control closed non-equilibrium quantum many-body systems may pave the way to the development of quantum technologies,while periodic kicking,as a special time-periodic driven system, provides a new kind of controllable system,which may also suggest new methods in controlling on the other quantum many-body systems.

Acknowledgment

This work was supported by the National Natural Science Foundation of China(Grant No.11475037),and the Fundamental Research Funds for the Central Universities (Grant No.DUT19LK38).

Appendix A: Some physical quantities used to characterize the Floquet DQPTs

In the main text, we have used the following physical quantities to characterize the emergence of Floquet DQPTs.Here,we give a brief introduction about these physical quantities.

(1)Return amplitude of Floquet DQPTs As we know,Loschmidt echo,or the return amplitude,has been widely used to identify DQPTs,[12,16]which is defined by the overlap between the initial state and its time-evolved state out of equilibrium.For the initial state|ψ(k,0)〉, the return amplitude at a later timetcan be obtained by

which tell us that,in the case that the finial state is orthogonal to the initial state,Gk(t)=0,the corresponding values in parameter space will result in a non-analyticity in the associated dynamical free energy,and form a dense set of thermodynamic limits.It has been studied that,when this set crosses the imaginary time axis at a critical time,a real-time Fisher zero ofGk(t)will appear.[18]This is analogue to the Lee–Yang theory of the phase transitions.In the following study,the return amplitude will also be used to show the non-analyticity in time-domain for the Floquet DQPTs.

(2)Rate function of return amplitude For theNlattice sites in the spin chain, the rate function of return amplitude|Gk(t)|for a many-particle Floquet state is defined as

In the case of ln|Gk(t)|2diverging,f(t) will disappear at a certain critical time and momentum, thus the rate function of the return amplitude can be used to characterize the Floquet DQPTs by revealing the existence of the non-analytical integral value in the range ofT ∈(0,2π).

(3)Pancharatnam geometric phase The Pancharatnam geometric phase is given by the difference between the total phase of the return amplitudeGk(t) and the dynamic phase,under non-adiabatic conditions,i.e.,

(4) Dynamical topological order parameter Dynamical topological order parameter (DTOP) is proposed to characterize the emergence of DQPTs,[26]which is dynamically defined in the real-time evolution of a quantum many-body system, represented by a momentum space winding number of the Pancharatnam geometric phase of the Brillouin zone,i.e.,

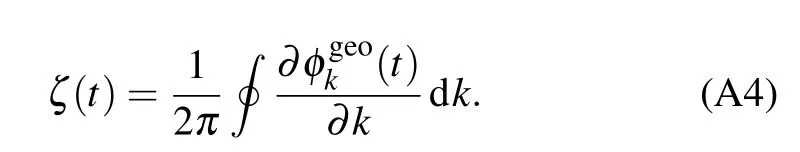
Becauseshows aπphase flip at the critical momentum in the momentum-time plane,the DTOP sticks to a quantized value generally and shows a jump of unit magnitude at every DQPT,i.e.,DTOP can change its integer value at discrete times where the so-called dynamical quantum phase transitions occur.Sinceζ(t)makes a quantization jump when time passes the critical time of the Floquet DQPT,DTOP serves as a dynamical analog of an order parameter,and is capable of resolving if the topology of the system Hamiltonian has changed over the kicking.