Jie Wang(王杰), Jun-Cheng Liang(梁俊成), Zi-Fa Yu(魚自發(fā)), An-Qing Zhang(張安慶),Ai-Xia Zhang(張愛霞), and Ju-Kui Xue(薛具奎)

College of Physics and Electronics Engineering,Northwest Normal University,Lanzhou 730070,China

Keywords: spin–orbit coupled spin-1 Bose–Einstein condenses,collective excitations,nonlinear modes coupling

1.Introduction

Ultra-cold atomic gases provide an ideal platform for exploring novel spin–orbit(SO)coupling physics,owing to their unprecedented levels of control[1–4]and precision in experiments.In ultra cold atomic gases, SO coupling can be generated by the two-photon Raman coupling technique.[5–9]Recently,SO-coupled spin-1 Bose–Einstein condensates(BECs)have been successfully achieved in experiments through Raman coupling among three hyperfine states of atoms,[2,10]thus paving the way to explore the rich physics of SO-coupled spin-1 BECs.Theoretical predictions and experimental observations of SO-coupled spin-1 BECs render various novel ground-state phases including plane wave phase, stripe phase and zero-momentum phases,etc.[11–14]

The collective excitation also provides an effective tool for exploring the physics of the condensates,and can be used to identify the phase transition of the system dynamically.The collective excitation of the spin-1/2 BECs with SO coupling has been widely and deeply explored experimentally[7,15]and theoretically[16,17]by using the sum rule approach[18]and the Bogoliubov spectrum analysis.[19]It is found that the collective dynamics is trivial for conventional condensates and the collective oscillation is harmonic.[20,21]However, the collective dynamics of the trapped spinor BECs is complex.Meanwhile,because of emergence of nonlinearity,a lot of interesting phenomena in the collective excitations of BECs,such as frequency shift,[22]mode coupling,[23–25]damping,[26,27]collapse and revival of oscillations,[28,29]are observed.

Recently, elementary excitations of SO-coupled spin-1 Boses gases are studied in free space, and it is found that phonon modes of different phases have different structures of rotons.[12,13,30]Noticeably, in trapped SO coupling spin-1 cold-atomic systems, an analogy of Hall response can be detected through collective excitations.[31]In Ref.[32],the collective excitation of a quasi-one-dimensional SOcoupled spin-1 BEC at finite temperatures for antiferromagnetic spin interactions was studied by utilizing the Hartree–Fock–Bogolyubor–Popov approximation.Moreover, the spin dynamics of spin-1 condensates in an external magnetic field is studied,[33]which exhibits a variety of periodic oscillations and provides theoretical support for interactions-driven oscillations.In general, because of coupling effects (induced by SO coupling and Raman coupling) and strong nonlinearity(induced by density-dependent interaction and spin-dependent interaction),rich nonlinear modes coupling(harmonic,anharmonic and irregular dynamics) should exist in SO-coupled spin-1 BECs.Accordingly,the nonlinear modes coupling will result in rich nonlinear spin dynamics.However, those are still open subjects.Particularly, the physical mechanism of generating anharmonic collective dynamics and the transition of harmonic-anharmonic dynamics in different phases of the system are still unclear.

In this paper, we study collective dynamics of SOcoupled spin-1 BECs in harmonic potential bath analytically and numerically.Using variational approaches, the coupled equations of motions for the center-of-mass coordinate of the condensate and its width are derived.Then, two low energy excitation modes in breathing dynamics and dipole dynamics are obtained analytically,which are in agreement with the numerical results of solving the Gross–Pitaevskii equation.We find that the dipolar dynamics for center-of-mass motion and the breathing dynamics for width variation of condensate are coupled through the spin dynamics induced by the SO coupling.This leads to the emergence of multiple external collective modes.Thus,the dipolar and breathing oscillation will be the superposition of the multiple harmonic oscillations,which generates an anharmonic collective dynamics.Furthermore,in anharmonic oscillations, breathing oscillations can be induced by excited dipole oscillations, and vice versa.Interestingly, spin-dependent interactions play an important role in collective excitation.In dipole dynamics, two degenerate low-energy excitation modes become non-degenerate as spindependent interaction increases.In breathing dynamics,however,when spin-dependent interaction is absent,the breathing dynamics is decoupled from spin dynamics and dipole dynamics, in which the breathing oscillation is harmonic.Particularly, we find that the collective dynamics is distinct in different phases,which is revealed both analytically and numerically.

The paper is organized as follows.In Section 2, based on the mean field approximation, we obtain the Hamiltonian of SO-coupled spin-1 BECs in a quasi-one-dimensional harmonic potential.In Sections 3 and 4,the variational equation of the system is obtained by minimizing the Lagrange density and the ground state phase of the system is analyzed in detail.In Sections 5, two low energy excitation modes in dipole dynamics and breathing dynamics are obtained analytically and verified numerically.Then the physical mechanism causing the anharmonic oscillation is discussed and the coupling effect of spin dynamics and breathing dynamics is emphasized,which leads to the phenomenon that the dipole (breathing)mode induces the breathing(dipole)mode in anharmonic oscillation.Finally in Section 6 we present conclusions.

2.The model

We study the collective dynamics of SO-coupled spin-1 BECs in harmonic potential.The SO coupling is characterized by equally weighted Rashba and Dresselhaus SO coupling.[7]The SO coupling only exists in the ?xdirection and mainly affects the collective dynamics in the ?xdirection, while the dipole oscillations in the ?yand ?zdirections are still harmonic oscillations,and the oscillation frequency is the harmonic potential frequency in that direction.Furthermore, when the strength of the trapping potential in the ?yand ?zdirections is much larger than the frequency of the trapping potential in the ?xdirection, the transverse degrees of freedom of the system are frozen such that the dynamics of the system only occurs in the ?xdirection.Therefore, we consider the onedimensional case and discuss the nonlinear mode coupling caused by SO coupling in the ?xdirection.According to the recent experiments[34,35]about the realization of SO-coupled spin-1 BECs, the dynamics of the BECs trapped in harmonic trap can be expressed by a dimensionless mean-field Gross–Pitaevskii equation (GPE) for normalized spinor wave functionΨ=(ψ1,ψ0,ψ-1)Tas[13,36]

3.The variational analysis

Now, the selection of the proper form of the trial functions is crucial.In our case, a natural choice is a Gaussian,i.e.,we take

whereφ(x)is a normalized Gaussian function

with the widthR, the center-of-mass positionx0, momentumkalong ?xdirection and the variational rate of radiusδof the wave packets.Here,αandβare variational parameters of the related phases of the two spin states.In particular, the average spin polarization〈Fz〉=M=∫(|ψ1|2-|ψ-1|2)dxand spin tensorcan be measured in experiment.Notice that the parameters(R,k,δ,α,β,x0,M,mz)are all time dependent.The nonlinear dynamics is controlled by a set of coupled Gross–Pitaevskii equations.However, the problem of solving the Gross–Pitaevskii equations can be formulated as a variational problem that minimizes the Lagrangian density.Upon substitute the spinor wave function into the Lagrangian￡=∫[(i/2)(Ψ*˙Ψ-Ψ˙Ψ*)-Ψ*(h0+hint)Ψ]dx,one can obtain

where

Applying the Euler–Lagrangian equations?￡/?qi-d(?￡/?˙qi)/dt=0, whereqi={k,R,M,mz,x0,α,β,δ}, we arrive at

Equations (6)–(9) describe the wave packet dynamics of the system, while Eqs.(10)–(13) give the spin dynamics of the system.It is clear that, because of spin-momentum locking and spin-dependent interaction [Eqs.(7), (10), and (11)], the wave packet dynamics and the spin dynamics are coupled.As discussed in the following sections, the ground state and the dynamics of the system are well described by the Eqs.(6)–(13).The variational analysis with Gaussian ansatz is widely used in studying the dynamics of trapped interacting Bose gas.In literature,[43,44]an intensive study of the reasonability of Gaussian ansatz and variational method was also provided.The reasonability of our variational results obtained with Gaussian ansatz(3)is further well confirmed by numerical simulations of the full GPE(1).

4.The ground state

The ground state of the system can be obtained by solving the equations of steady state,i.e., ˙qi=0.We find the SO coupled BECs condensate into the momentum statek=kmin=2γM.Thus, the ground state phases of the system can be determined by the order parameterM.WhenM=0, the condensates are in zero momentum state.On the contrary, whenM/=0, the condensates are in nonzero momentum state.In addition,by substituting the solutions of the steady state equations into Eq.(5),we can numerically obtain the ground state energy of the system.Then, the ground states of the system can be determined.

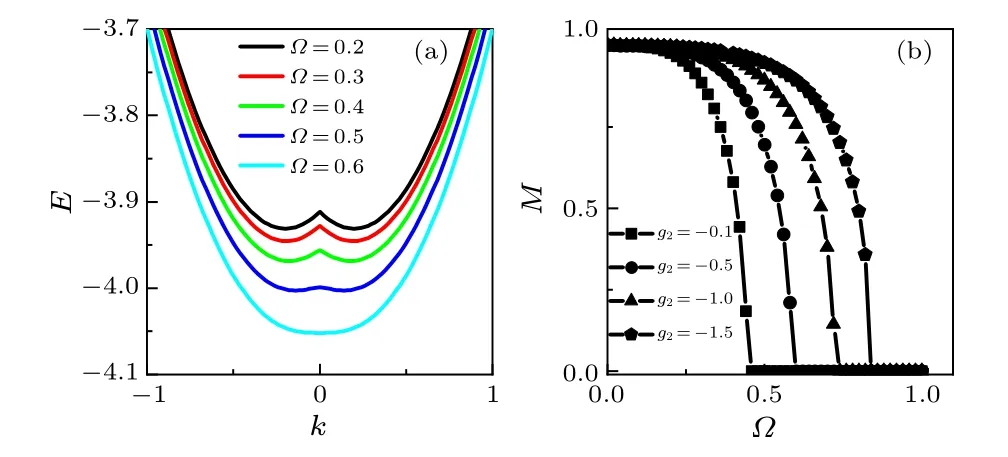
Fig.1.(a)The energy band of the system as a function of k for different Ω with g2=-0.5.(b)The average spin polarization|M|against Ω for different g2.We set g0=1,γ =0.1,ω =0.1,and Δ =-4.

To identify the ground state phases of the system,we plot the energy band structure and average spin polarization|M|with differentΩin Fig.1.It is obvious that,withΩincreasing, the spin polarizationMdecreases from a finite value to zero and the band structure changes from a double degenerate minimum withk/= 0 to a single degenerate minimum withk= 0.This proves that the system has undergone a phase transition.ForM/=0, the atoms condense in thek=±2γMstate, the energy band structure has a double well structure.In this case, there are different numbers of atoms in the two spin statesmF=1 andmF=-1,thus the condensates are in a magnetized state(spin polarized state)with nonzero momentum.ForM=0, the atoms condense in the zero momentum state,and the band structure presents a parabolic structure.In this case,the two spin statesmF=±1 have the same number of atoms, thus the condensates are in an unmagnetized state with zero momentum.

5.The collective excitation

To analyze the dipolar and breather modes, we consider the weak perturbation around the equilibrium stateqi0of Eqs.(6)–(13).Substitutingqi=qi0+δqiinto Eqs.(6)–(13),the linearized equations for collective dynamics are acquired as follows:

5.1.Dipolar dynamics

Firstly, we only focus on the dipolar oscillation, and assume that the width of condensate still remains unchanged under the weak excitation,i.e.,δR=0.Based on Eqs.(14)–(16),one can obtain

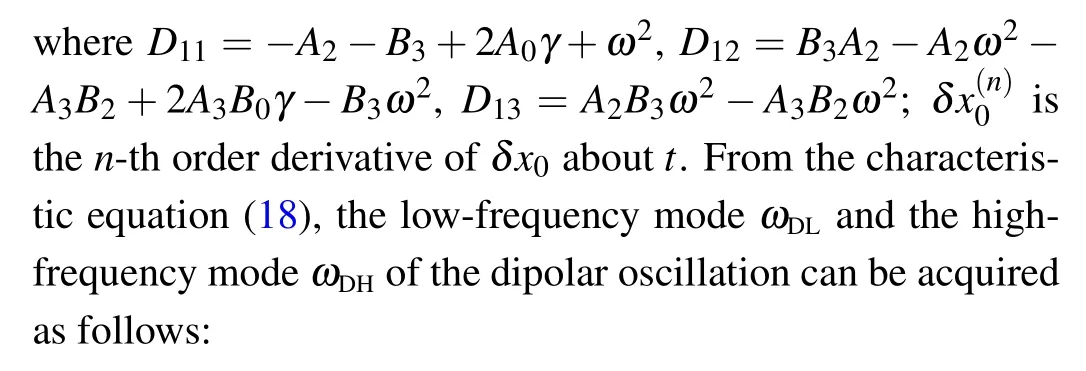
where

and the dipolar oscillation can be described by

withδx0being the initial deviation of the center-of-mass from the equilibrium position.

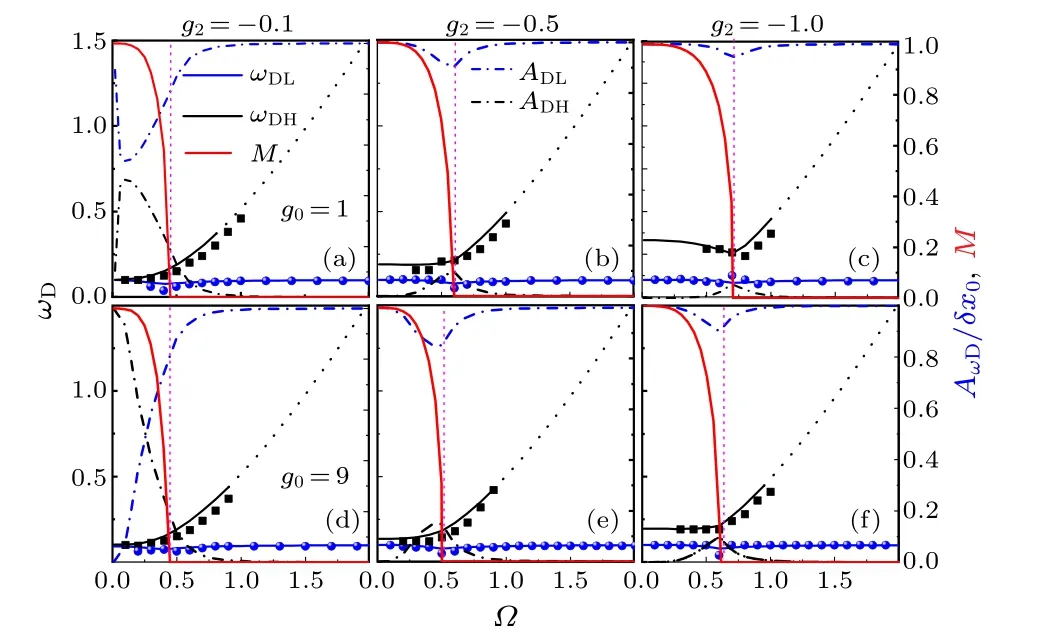
Fig.2.Frequency and the corresponding amplitude of the dipolar oscillation versus Ω for different g0 and g2,where γ =0.1,Δ =-4,and ω =0.1: (a)–(c)for g0 =1, (d)–(e)for g0 =9.The corresponding M in the ground state is represented by the solid red line,the dashed black line is the higher-frequency mode with zero amplitude.The results of direct numerical simulation of GPE(1)is represented by symbols.The red dashed line marks the phase transition point.

For a conventional condensate, the dipolar oscillation is trivial, its frequency is just the harmonic-trap frequency and is independent of SO coupling, RC and inter-atomic interactions.However, for an SO coupled condensate, the dipolaroscillation frequency is different from the trapping frequency.The coupling effect of SO coupling, RC and atomic interactions is generation of two external dipolar modes, which can lead to the dipolar dynamics in the superposition of the two harmonic oscillations.When one of the two external frequencies is the inherent frequency, and the amplitude of the other external frequency vanishes, the dipolar oscillation is harmonic, otherwise it is the anharmonic dipolar oscillation.Whether the dipolar oscillation is harmonic depends on the competition between the two external modes, this is demonstrated in Eqs.(21) and (22) and clearly shown in Fig.2.In Fig.2, the phase transition pointΩ=Ωcis represented byM=0.WhenΩ=0 and|g2| is small [see Figs.2(a) and 2(d)],the two modes degenerate to the trapping frequency,i.e.,ωDL=ωDH=ω.With the increase of|g2|,the two degeneracy frequencies are split apart,and the larger the|g2|is,the more obvious the split is.However,the largerg0weakens the effect ofg2onωDH[see Figs.2(d)–2(f)].As shown in Fig.2, the lower-frequency modeωDLdoes not change much and keeps at trapping frequency asΩincreases, i.e.,ωDL～=ω, whereas the higher-frequency modeωDHalways increases withΩ, especially in theΩ ＞Ωcregion.When the system is deeply in the unmagnetized phase (Ω ?Ωc), the dipolar oscillation is harmonic withωDL=ω(ADL=1 andADH=0).However,around the phase transition point (Ω ≈Ωc), the collective excitation of the system is complicated and anharmonic.In this case, many modes will be excited.When the system is in the fully magnetized phase (Ω ?Ωc), the amplitudeADHcorresponding to modeωDHdisappears and the dipolar oscillation is also harmonic withωDL=ω.In this case,M →1 andmz →1,nearly all atoms condense in the spin state ofmf=1(i.e.|Ψ-1|2→0,|Ψ0|2→0 and|Ψ1|2→1),it can be approximated that the system is nearly one-component,spin dynamics disappears,so dipolar oscillation is harmonic.

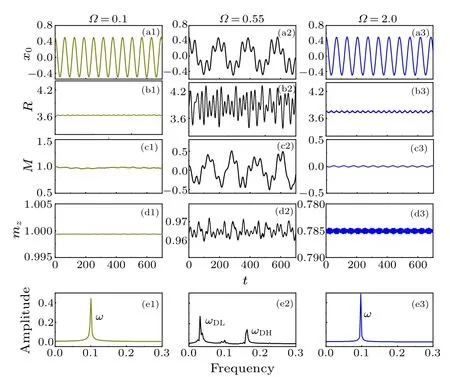
Fig.3.The dipolar dynamics started in the fully magnetized phase with Ω =0.1(a1)–(e1),in the magnetized phase near phase transition point with Ω =0.55 (a2)–(e2), and in the deep unmagnetized phase with Ω =2.0(a3)–(e3).(e1)–(e3)The corresponding spectrum analyses of dipolar oscillation.We set γ=0.1,g0=1,g2=-0.5,δx0=0.5,δR=0,ω =0.1,and Δ =-4.

To confirm the variational prediction,with small displacement of the center mass position of wave packets from the ground state, we perform direct numerical simulations of full GPE(1)using the fourth-order Runge–Kutta method,and the dipolar dynamics in the different phase regions is depicted in Fig.3.Meanwhile, the numerical results of the two dipolar modes are also shown in Fig.2, we find that the variational results are in good agreement with the numerical simulations.When the condensates are perturbed in nearly fully magnetized phase[see Figs.3(a1)–3(e1)],as predicted by variational analysis[see Fig.2],the amplitude of higher-frequency modeADHis zero, the dipolar oscillating is harmonic withωDL=ω[see Fig.3(e1)].In this case,M →1 andmz →1[see Figs.3(c1)–3(d1)], the spin dynamics disappears, the breathing dynamics cannot be excited,R ≈R0[see Fig.3(b1)].When the condensates are excited in a magnetized phase near the phase transition point[see Figs.3(a2)–3(e2)],where the dipolar dynamics and the breathing dynamics are strongly coupled due to SO coupling [see Eqs.(14)–(17)], the dipolar oscillation is anharmonic and its oscillation frequency is the superposition of two modesωDLandωDH[see spectrum analysis in Fig.3(e2)].In addition, the dipolar dynamics induces complex and irregular breathing dynamics and spin dynamics[see Figs.3(b2)–3(d2)].When the condensates are excited in the deep unmagnetized phase [see Figs.3(a3)–3(e3)], where the dipolar dynamics and the breathing dynamics are decoupled due toM=0 [see Eqs.(14)–(17)], the dipolar oscillating is harmonic, the dipolar dynamics cannot induce the breathing dynamics and spin dynamics[see Figs.3(b3)and 3(d3)].

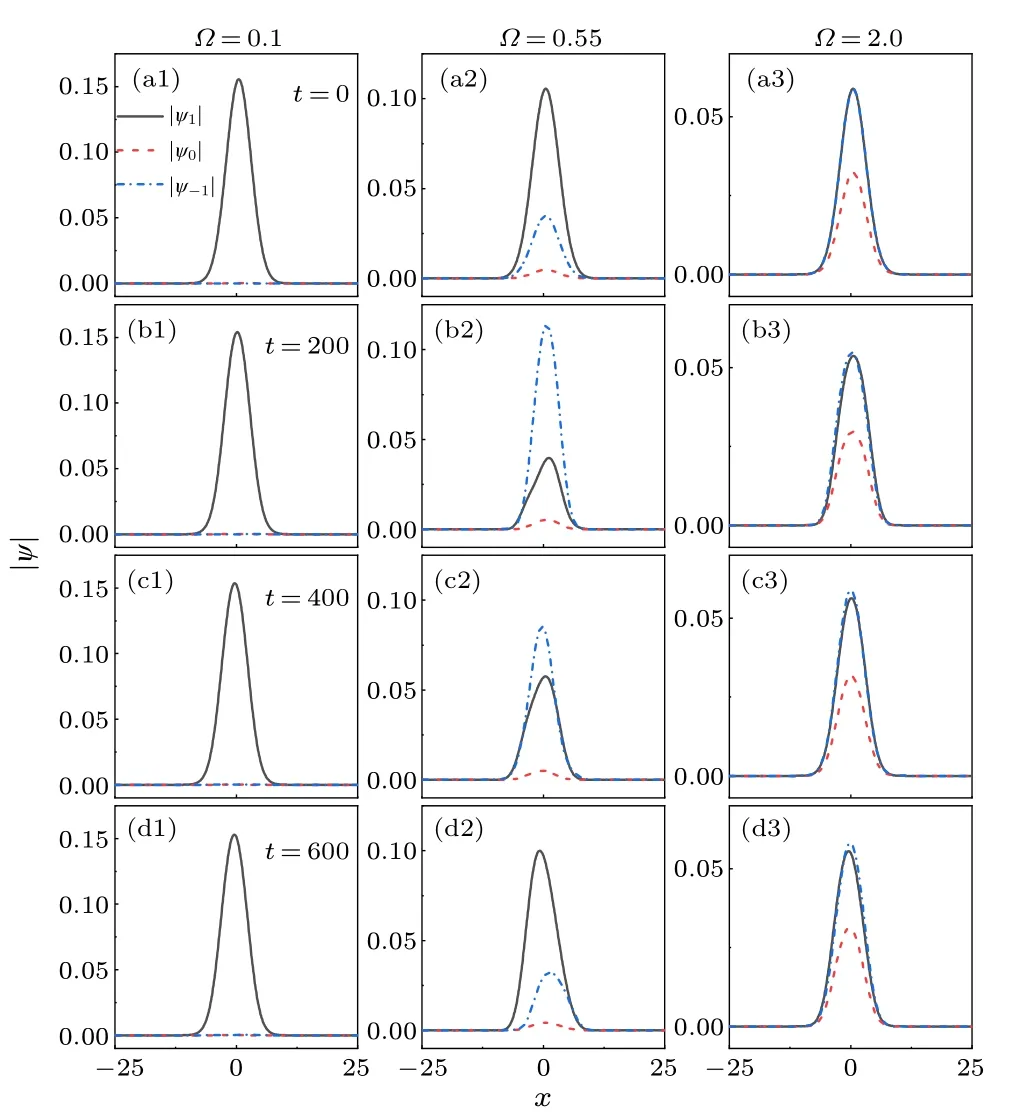
Fig.4.Time evolution of the three pseudo spin states |ψ1|, |ψ0| and|ψ-1| in the fully magnetized phase with Ω =0.1 (the first column),in the unmagnetized phase near phase transition point with Ω =0.55(the second column) and in the deep magnetized phase with Ω =2.0(the third column).We set g0 =1, g2 =-0.5, γ =0.1, ω =0.1, and Δ =-4.

The corresponding wave packets in different ground state phases are shown in Fig.4.The wave packets|ψ1|,|ψ0| and|ψ-1| are always Gaussian like.In the case of full magnetized phase[see Figs.4(a1)–4(d1)],M →1,mz →1,only one component|ψ1| exists and there is almost no spin exchange between the spin components|ψ1| and|ψ-1|.However, in the magnetized phase near phase transition point,the dynamic behaviors of two pseudo spin components|ψ1|and|ψ-1|are different[see Figs.4(a2)–4(d2)],the strong spin exchange can be observed evidently.In addition,|ψ1|and|ψ-1|are almost coincided in the deep unmagnetized phase [see Figs.4(a3)–4(d3)],M=0, the spin exchange between two pseudo spin components is very weak in this case.We conclude that strong spin dynamic induces strong coupling of dipolar and breather modes,which results in anharmonic and complex wave packets dynamics and spin dynamics.The numerical simulation confirm the variational predictions.

5.2.Breathing dynamics

When considering the breathing dynamics under the weak excitation, the mass center of condensates can be regarded to be at rest, i.e.,δx0=0.Based on Eqs.(15)–(17), one can obtain

whereD21=-(A2+B3+C1),D22=-A1C2-A3B2+A2B3+A2C1+B3C1-B1C3,D23=A1B3C2-A1B2C3+A3B2C1-A2B3C1-A3B1C2+A2B1C3;δR(n)is then-th order derivative ofδRaboutt.From Eq.(23), the low-frequency modeωBLand the high-frequency modeωBHof the breathing oscillation can be acquired as follows:

where

The breathing oscillation can be described by

where

withδR=R-R0being the deviation of width fromR0initially.

The inherent frequency of the breathing oscillation for a conventional condensate iswhich depends on the harmonic trapping and atomic interactions.However, the breather modes are complex for spinor BECs, which is related to SO coupling, RC, harmonic trapping, and atomic interactions.Obviously, under a weak excitation,the breathing dynamics of trapped BECs with SO coupling is also the superposition of the two harmonic oscillations with frequenciesωBLandωBH.The competition of the two breather modes is clearly depicted in Fig.5.

Similar to dipolar dynamics, when one of the two external frequencies is the inherent frequency, and the amplitudes of the other external frequencies vanish [see Eqs.(27a) and(27b)], the breathing oscillation is harmonic, otherwise it is anharmonic.Whether the breathing oscillation is harmonic depends on the competition between the two external modes,which is demonstrated in Eqs.(26) and (27).In addition,the spin-dependent interactiong2has an important effect on breathing dynamics.In particular, wheng2= 0, breathing dynamics is decoupled not only from spin dynamics but also from dipolar dynamics due to coefficientsC2=0 andC3=0[see Eq.(17) or Eqs.(8) and (9)].In this case, the breathing oscillation is also harmonic withωB0.Meanwhile, different from the dipolar mode, the two breather modes do not degenerate wheng2is small andg2only has a greater influence onωBHmode.However,the largerg0weakens the effect ofg2onωDH[see Figs.5(d)–5(f)].As shown in Fig.5, the lower-frequency modeωBLalways varies around the inherent frequencyasΩincreases.Contrarily, the higherfrequency modeωBHalways increases withΩ, especially in theΩ ＞Ωcregion.When the system is in the fully magnetized phase(Ω ?Ωc),M →1,mz →1,spin dynamics disappears,the breathing dynamics is harmonic with high-frequency modeωBH.The breathing dynamics around the phase transition point(Ω ≈Ωc)is also complex for the reasons similar to that of the dipolar mode,i.e.,strong coupling of breathing dynamics and spin dynamics occurs.However, when the system is deeply in the unmagnetized phase (Ω ?Ωc),M=0, the spin and breathing dynamics are decoupled,the breathing oscillation is also harmonic withωBL～=ωB0(ABL=1 andABH=0).

Fig.5.The same as Fig.2 but for the breathing oscillation.

To prove the variational predictions, with the weak perturbation of wave packet width from the ground state, the breathing dynamic behaviors of different phase regions are obtained by numerical simulation [see Fig.6].Meanwhile,the numerical simulation results of the two breather modes are also shown in Fig.5.We find that variational results are also in good agreement with the numerical simulations.When the condensates are disturbed in nearly fully magnetized phase [Figs.6(a1)–6(e1)], as predicted by variational analysis [Fig.5], the amplitude of lower-frequency modeωBLis zero, and the breathing oscillation is harmonic withωBH.In this case,the dipolar dynamics and spin dynamics are not excited [see Figs.6(b1)–6(e1)].When the condensates are excited in a magnetized phase around the phase transition point,the breathing oscillation is anharmonic[see Fig.6(a2)]due to dipolar dynamics and spin dynamic behaviors are excited[see Figs.6(b2)and 6(c2)].At the same time,breathing oscillation frequency is the superposition of two frequenciesωBLandωBH[see spectrum analysis in Fig.6(e2)].When the condensates are excited in the deep unmagnetized phase[see Figs.6(a3)–6(e3)],where the breathing dynamics and the dipolar dynamics are decoupled due toM= 0 [see Eqs.(14)–(17)], the breathing oscillation is harmonic,and the breathing dynamics cannot induce the dipolar dynamics and spin dynamics [see Figs.6(b3)–6(e3)].Interestingly, in this case, although the spin tensormzis excited, it has weak effect on the collective dynamic of the system.

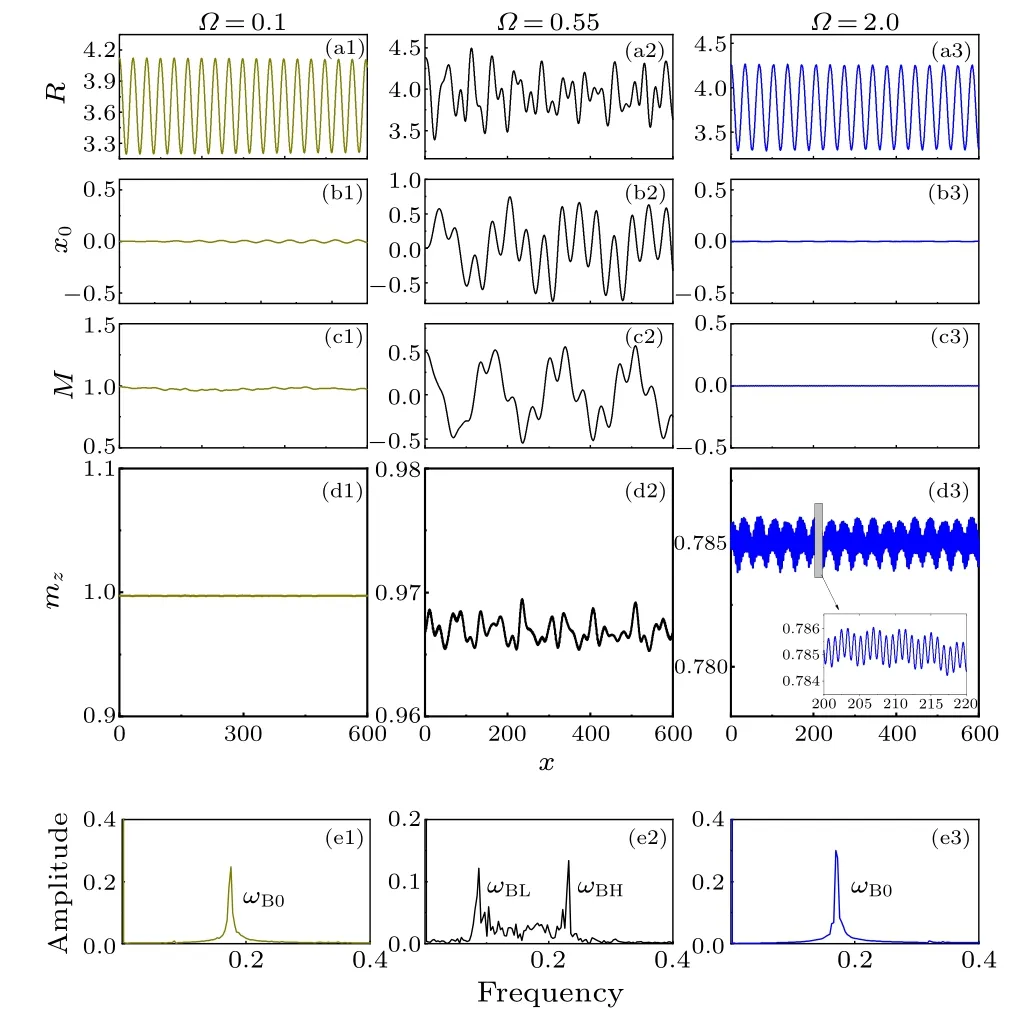
Fig.6.Breathing dynamics started in the fully magnetized phase with Ω =0.1(a1)–(e1),in the magnetized phase near phase transition point with Ω = 0.55 (a2)–(e2), and in the deep unmagnetized phase with Ω =2.0(a3)–(e3).(e1)–(e3)The corresponding spectrum analyses of breathing oscillation.We set g0 =1, g2 =-0.5, γ =0.1, δR=0.5,δx0=0,ω =0.1,and Δ =-4.The inset in(d3)is a larger view of the gray area.

In breathing dynamics, the corresponding wave packets dynamics in different ground state phases are shown in Fig.7.In the fully magnetized phase [Figs.7(a1)–7(d1)],M →1,mz →1, the condensates keep in themF=1 state during the breathing dynamics.The numerical results well confirm the variational predictions.In the magnetized phase near phase transition point [Figs.7(a2)–7(d2)], the wave packets of the two spin components|ψ1| and|ψ-1| are obviously different,and there is an obvious spin exchange between|ψ1|and|ψ-1|during the time evolution.However,in the deep unmagnetized phase[Figs.7(a3)–7(d3)],M=0,the wave packets of the two spin components|ψ1|and|ψ-1|almost coincide,and there is no spin exchange between|ψ1| and|ψ-1| in the time evolution.

Fig.7.Time evolutions of the three pseudo spin states |ψ1|, |ψ0| and|ψ-1|in the fully magnetization phase with Ω =0.1(the first column),in the magnetized phase near phase transition point with Ω =0.55(the second column)and in the deep unmagnetized phase with Ω =2.0(the third column).We set g0=1,g2=-0.5,γ=0.1,ω=0.1,and Δ=-4.

6.Conclusions

In summary,we have characterized the collective excitations of interacting SO-coupled spin-1 BECs in harmonic potential.We analytically predict the dipolar and breather modes in collective excitations,which are well confirmed by the numerical results.The collective behaviors of the BECs can be regarded as the superposition of the multiple harmonic oscillations induced by the coupling effects of SO coupling,RC and atomic interactions.Therefore, the collective oscillations can translate between harmonic and anharmonic, which depends on the competition of the multiple external collective modes.In addition,the dipolar dynamics and breathing dynamics can be coupled due to the cooperative effect of spin momentum locking and spin-dependent interaction, and behaves distinct characters in different phases.Interestingly, in anharmonic oscillations, breathing oscillations can be induced by excited dipole oscillations, and vice versa.Our results provide theoretical evidence for identifying, exploring and manipulating the ground sate phases and collective dynamics of a system experimentally.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos.12164042, 12264045,11764039, 11475027, 11865014, 12104374, and 11847304),the Natural Science Foundation of Gansu Province (Grant Nos.17JR5RA076 and 20JR5RA526),the Scientific Research Project of Gansu Higher Education (Grant No.2016A-005),the Innovation Capability Enhancement Project of Gansu Higher Education (Grant Nos.2020A-146 and 2019A-014),and the Creation of Science and Technology of Northwest Normal University(Grant No.NWNU-LKQN-18-33).

Appendix A: The dimensional reduction of the model

The GPE describing the three-dimensional trapped SOcoupled spin-1 BECs can be written as

whereΨ=(ψ1,ψ0,ψ-1)Tis the spinor wave function,px=-iˉh?x,p⊥=-iˉh(?y+?z),g0=4πˉh2(a0+2a2)/(3m),g2=4πˉh2(a2-a0)/(3m), ～Ωis the RC strength, and ～Δis the quadratic Zeeman strength.We consider an SO coupling characterized by an equally weighted Rashba and Dresselhaus SO coupling.The SO coupling only exists in the ?xdirection and mainly affects the collective dynamics in the ?xdirection, while the dipole oscillations in the ?yand ?zdirections are still harmonic oscillations, and the oscillation frequency is the harmonic potential frequency in that direction.Furthermore,when the strength of the trapping potential in the ?yand ?zdirections is much larger than the frequency of the trapping potential in the ?xdirection,the transverse degrees of freedom of the system are frozen such that the dynamics of the system only occurs in the ?xdirection.Therefore, we consider the one-dimensional case and discuss the nonlinear mode coupling caused by SO coupling in the ?xdirection.The threedimensional wave function can be decomposed into

where

A constant is ignored in Eq.(A4).Comparing Eqs.(A4)with(A1), we can find that the dimensional reduction of the GPE only causes a correction for the strength of interactions.

The obtained dimensionless parameters can be estimated according to the relevant experimental parameters.[7,34,39]Taking the wavelength of the Raman laser asλR= 804.3 nm,trapped potential frequencyωx=2π×20 Hz andωy=ωz=2π×400 Hz and atomic numberN=10000, then the oscillator lengths in the ?xdirection and the transverse direction arel0=2.41 μm andl⊥=0.571 μm, respectively; SO couplingγ～4, RC strengthΩ～0–100 and quadratic Zeeman strength|Δ|～0–35 are experimentally adjustable to a large extent.For87Rb atoms, the scattering lengtha0=5.387 nm anda2=5.313 nm,then the reduced density-dependent interactiong0～200 and spin-dependent interactiong2～-1 can be obtained.However, for23Na atoms, the scattering lengtha0=2.646 nm anda2=2.919 nm,theng0～53 andg2～2.Therefore, the physical parameters used in this paper are all within the ranges of experimental parameters.

Appendix B:Linearization coefficients

The linearization coefficients mentioned in Section 3 are given as follows:

whereM,mzandRare taken in the ground state and are determined by Eqs.(6)–(13).