北京師范大學(xué)貴陽(yáng)附屬中學(xué) (430079) 李嘉鈴

1.預(yù)賽試題

題目(2022年全國(guó)高中數(shù)學(xué)聯(lián)賽四川預(yù)賽第6題)若△ABC的三邊a,b,c滿(mǎn)足a2+b2+3c2=7,則△ABC面積的最大值為.

這是一道只有一個(gè)條件的求三角函數(shù)面積的最值問(wèn)題,注意到已知等式中a,b,c均帶平方,且a與b是對(duì)稱(chēng)的,所以在選擇面積的表示方法時(shí)就要充分考慮到這些因素,為下一步求最大值做好鋪墊.

2.多解探究

記△ABC面積的最大值為S.

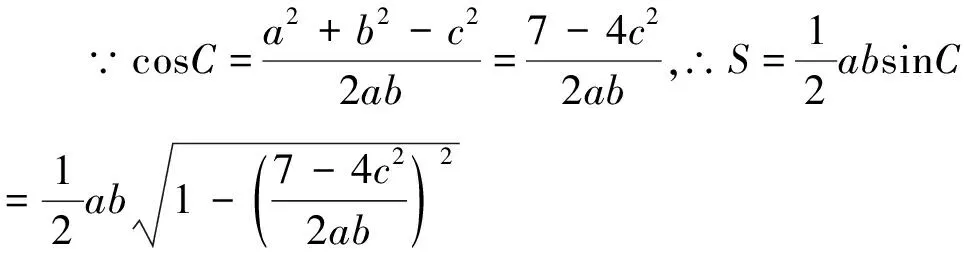
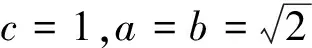
解法2：(利用海倫—秦九韶公式,再轉(zhuǎn)為二次函數(shù)處理)

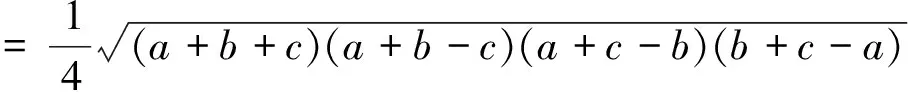
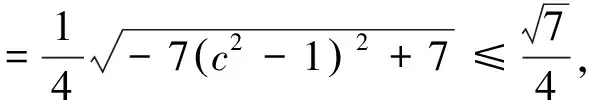
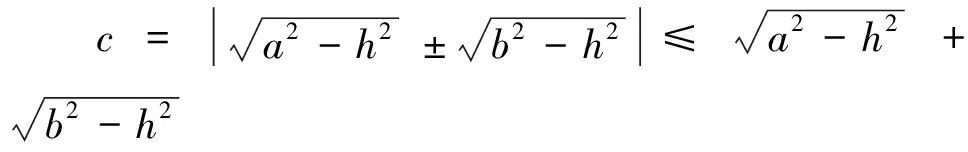
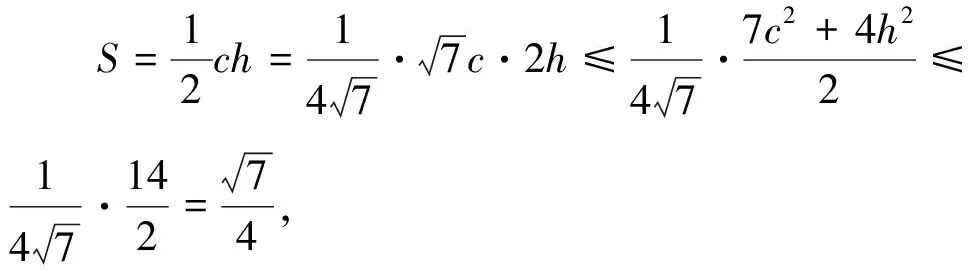
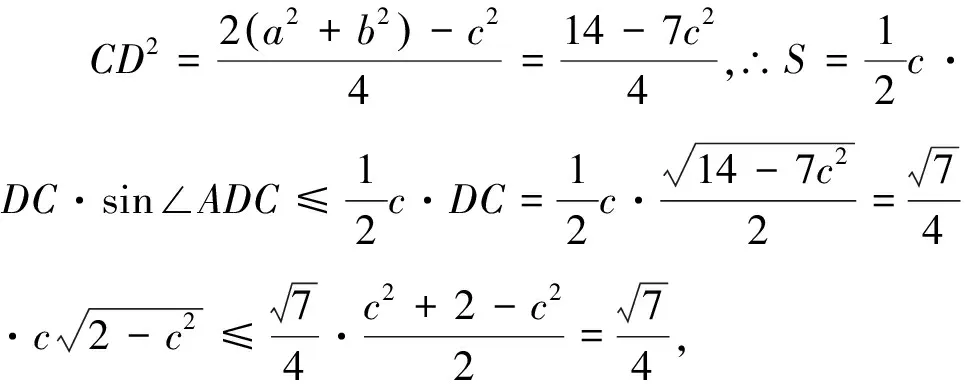
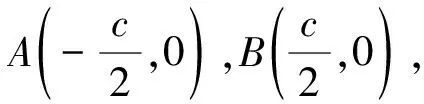
3.題后反思

這五種解法都包含兩個(gè)主要方面:面積的表示方法和求最大值的方法.

(1)面積的表示方法.因?yàn)槿切蔚拿娣e公式比較多,而且用同一個(gè)公式也有不同的切入點(diǎn),這就導(dǎo)致了這類(lèi)題的解法多樣,這五種方法就是這樣產(chǎn)生的.不同的表示方法也基本決定了后面解題過(guò)程的走向和難易程度,所以選一個(gè)好的表示方法很重要.

(2)求最大值的方法.這五種方法求最大值的過(guò)程看起來(lái)都不一樣,但基本方法其實(shí)有共同之處:都對(duì)式子進(jìn)行放縮,直到得出定值,最后確定等號(hào)成立的條件;放縮的方法主要是基本不等式和一些常見(jiàn)結(jié)論.所以,解這類(lèi)題至關(guān)重要的是放縮對(duì)象的選擇和基本不等式的選用,而基本不等式的選用又取決于放縮對(duì)象的特點(diǎn)和題中的條件.那么,只要掌握了選擇放縮對(duì)象的方法,基本就等于掌握了解這類(lèi)題的鑰匙.因?yàn)槌晒Φ姆趴s必須保證等號(hào)能成立,而基本不等式一般有兩大特點(diǎn):式子具有對(duì)稱(chēng)性,等號(hào)成立的條件多數(shù)是變量相等.注意到條件a2+b2+3c2=7中a和b是對(duì)稱(chēng)的,所以,五種解法都把由a和b組成的對(duì)稱(chēng)式作為放縮的對(duì)象,這樣能保證等號(hào)成立.

從以上分析可知,選擇一種好的表示方法和(在有對(duì)稱(chēng)變量的情況下)構(gòu)造出對(duì)稱(chēng)式作為放縮對(duì)象就是解這類(lèi)問(wèn)題的鑰匙.