不定方程的正整數(shù)解
管訓貴, 潘小明
(泰州學院 數(shù)理學院,江蘇 泰州 225300)
設a,b,c為兩兩互素的正整數(shù)且滿足a2+b2=c2,則對任意的正整數(shù)n,丟番圖方程
(na)x+(nb)y=(nc)z
(1)
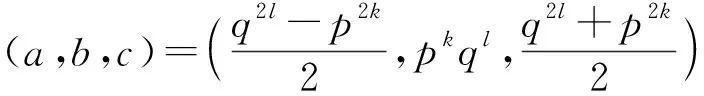
(2)
僅有正整數(shù)解(x,y,z)=(2,2,2). 但其余的情形較為復雜,本文對此進行了探究,給出一般性結果.
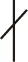
由定理1可得下列結論.
推論1對任意的正整數(shù)n,丟番圖方程
(576n)x+(943n)y=(1 105n)z
(3)
僅有正整數(shù)解(x,y,z)=(2,2,2).
1 若干引理
引理1[4]方程(1)適合(x,y,z)≠(2,2,2)且n>1的正整數(shù)解(x,y,z,n)必滿足下列條件之一:
(ⅰ) max{x,y}>min{x,y}>z;
(ⅱ)x>z>y;
(ⅲ)y>z>x.
引理2[5]方程(1)沒有適合max{x,y}>min{x,y}>z且n>1的正整數(shù)解(x,y,z,n).
引理3[3]設k,l,m1,m2為正整數(shù),p,q為素數(shù)且滿足pk=2m1-3m2,ql=2m1+3m2.若(x,y,z)是丟番圖方程
的正整數(shù)解且x≡y≡z≡0(mod 2),則必有(x,y,z)=(2,2,2).
由引理3立即可得下列結論.
引理4丟番圖方程
576x+943y=1 105z
(4)
僅有正整數(shù)解(x,y,z)=(2,2,2).
證明對(4)式取模4得(-1)y≡1(mod 4),從而y≡0(mod 2).對(4)式取模64,有17z≡(-17)y≡17y(mod 64),即17|z-y|≡1(mod 64),得z-y≡0(mod 4),故z≡0(mod 2).對(4)式取模41,有2x≡(-2)z≡2z(mod 41),即2|x-z|≡1(mod 41),得x-z≡0(mod 20),故x≡0(mod 2).于是x≡y≡z≡0(mod 2),根據(jù)引理3,方程(4) 僅有正整數(shù)解(x,y,z)=(2,2,2). 證畢.
引理5[6]設r是大于1的奇數(shù),則方程
X2+Y2=Zr, gcd(X,Y)=1, 2|Y
(5)
的正整數(shù)解(X,Y,Z)都可表示為
其中:λ1,λ2∈{-1,1};X1,Y1是正整數(shù),gcd(X1,Y1)=1,2|X1Y1.
由引理5易得如下結論.
引理6方程(5)滿足條件的正整數(shù)解(X,Y,Z)可表示為
Z=A2+B2,
其中:A,B是正整數(shù),gcd(A,B)=1,2|A.
2 定理1的證明
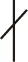
根據(jù)引理1和引理2可知,只需討論方程(2)在n>1且min{x,y} 情形1x>z>y. 此時方程(2)可化為 (6) 由于z>y,故gcd(n,pq)>1.設n=puqvn1,這里u+v≥1,gcd(n1,pq)=1,則(6)式變?yōu)?/p> (7) 由(7)式可知n1=1. 情形1.1若n=pu(u≥1),則ky=u(z-y).于是(7)式可化為 (2m1+13m2)xpu(x-z)= (22m1+32m2)z-(2m1+3m2)y. (8) 對(8)式取模3,有1≡(-1)y(mod 3),得y≡0(mod 2).令z=2z1,y=2y1,則由(8)式可得 2(m1+1)x3m2xpu(x-z)= ((22m1+32m2)z1+(2m1+3m2)y1)× ((22m1+32m2)z1-(2m1+3m2)y1). (9) 注意到gcd((22m1+32m2)z1+(2m1+3m2)y1,(22m1+32m2)z1-(2m1+3m2)y1)=2,有 2(m1+1)x-1|((22m1+32m2)z1+(2m1+3m2)y1)或 2(m1+1)x-1|((22m1+32m2)z1-(2m1+3m2)y1), 但2m1>3m2,推得 2(m1+1)x-1>2(m1+1)z= 22(m1+1)z1>(22m1+32m2+2m1+3m2)z1> (22m1+32m2)z1+(2m1+3m2)y1> (22m1+32m2)z1-(2m1+3m2)y1, 不可能.因此(9)式不成立,從而(8)式不成立. 情形1.2若n=qv(v≥1),則ly=v(z-y).于是(7)式可化為 (2m1+13m2)xqv(x-z)= (22m1+32m2)z-(2m1-3m2)y. (10) 對(10)式取模3,有1≡(-1)y(mod 3),得y≡0(mod 2).令z=2z1,y=2y1,則由(10)式可得 2(m1+1)x3m2xqv(x-z)= ((22m1+32m2)z1+(2m1-3m2)y1)× ((22m1+32m2)z1-(2m1-3m2)y1). (11) 類似于情形1.1的討論知(11)式不成立,從而(10)式不成立. 情形1.3若n=puqv(u≥1,v≥1),則ky=u(z-y),ly=v(z-y).于是(7)式可化為 (2m1+13m2)xpu(x-z)qv(x-z)=(22m1+32m2)z-1. (12) 由于z≡0(mod 2),所以(22m1+32m2+1)|(22m1+ 32m2)z-1.考慮到22m1+32m2+1≡2(mod 4),22m1+32m2+1≡2(mod 3),有 情形2y>z>x.此時方程(2)可化為 即 (2m1+13m2)x= nz-x((22m1+32m2)z-(22m1-32m2)yny-z). (13) 設n=2r3sn1,這里r+s≥1,gcd(n1,6)=1,則(13)式變?yōu)?/p> 2(m1+1)x3m2x= (14) 由(14)式可知n1=1,且 (22m1+32m2)z-(22m1-32m2)y2r(y-z)3s(y-z)= 2(m1+1)x-r(z-x)3m2x-s(z-x). (15) 情形2.1若r=0,s>0,則由(15)式得m2x=s(z-x),且有 (22m1-32m2)y3s(y-z)=(22m1+32m2)z-2(m1+1)x. (16) 令z=2z1,m1+1=2n1,則(16)式可化為 (22m1-32m2)y3s(y-z)= ((22m1+32m2)z1+2n1x)((22m1+32m2)z1-2n1x). (17) 注意到gcd((22m1+32m2)z1+2n1x,(22m1+32m2)z1- 2n1x)=1,有 (2m1+3m2)y|(22m1+32m2)z1+2n1x或 (2m1+3m2)y|(22m1+32m2)z1-2n1x, 但 (2m1+3m2)y>(2m1+3m2)z= (2m1+3m2)2z1>(22m1+32m2)z1+2n1x> (22m1+32m2)z1-2n1x, 不可能.因此(17)式不成立,從而(16)式不成立. 情形2.2若s=0,r>0,則由(15)式得(m1+1)x=r(z-x),且有 (22m1-32m2)y2r(y-z)=(22m1+32m2)z-3m2x. (18) 令z=2z2,m2=2n2,則(18)式變?yōu)?/p> (2m1+3m2)y(2m1-3m2)y2r(y-z)= ((22m1+32m2)z2+3n2x)((22m1+32m2)z2-3n2x). 注意到gcd((22m1+32m2)z2+3n2x,(22m1+32m2)z2-3n2x)=2,有 (2m1+3m2)y|(22m1+32m2)z2+3n2x或 (2m1+3m2)y|(22m1+32m2)z2-3n2x, 但 (2m1+3m2)y>(2m1+3m2)z= (2m1+3m2)2z2>(22m1+32m2+32n2)z2> (22m1+32m2)z2+(32n2)z2> (22m1+32m2)z2+3n2x>(22m1+32m2)z2-3n2x, 不可能. 因此(18)式不成立. 情形2.3若r>0,s>0,則由(15)式得(m1+1)x=r(z-x),m2x=s(z-x),且有 (22m1-32m2)y2r(y-z)3s(y-z)=(22m1+32m2)z-1. (19) 因為z≡0(mod 2),所以完全類似于情形1.3的討論知(19)式不成立. 綜上所述,定理1得證. 根據(jù)引理4知當n=1時結論成立.下設n>1. 易知b=23·41,此時k=l=1,pk=23=25-32,ql=41=25+32. (ⅰ)假定方程(3)有適合x>z>y且n>1的正整數(shù)解(x,y,z,n).由于b=23·41,故n=23u41v(u+v≥1).于是(3)式可化為 23y41y=23u(z-y)41v(z-y)× (1 105z-576x23u(x-z)41v(x-z)). (20) 若n=23u(u≥1),則y=u(z-y).于是(20)式可化為 576x23u(x-z)=1 105z-41y; (21) 若n=41v(v≥1),則y=v(z-y).于是(20)式可化為 576x41v(x-z)=1 105z-23y; (22) 若n=23u41v(u≥1,v≥1),則y=u(z-y)=v(z-y).于是(20)式可化為 576x23u(x-z)41v(x-z)=1 105z-1. (23) 根據(jù)定理1知只需證明(21)~(23)式中z≡0(mod 2)即可. 若(21)式成立,則y≡0(mod 2).假定z≡1(mod 2),由y=u(z-y)知u≡0(mod 2). 令u=2u1,y=2y1,則(21)式變?yōu)?/p> (24) 易知1 105=322+92=242+232=122+312=42+332=A2+B2,其中A∈{4,12,24,32},B∈{9,23,31,33}.根據(jù)引理6及(24)式可得 (25) 由(25)式知B|41y1,顯然不可能.因此z≡0(mod 2). 若(22)式成立,則y≡0(mod 2).假定z≡1(mod 2),由y=v(z-y)知v≡0(mod 2). 令v=2v1,y=2y1,則(22)式變?yōu)?/p> (26) 易知1 105=322+92=242+232=122+312=42+332=A2+B2,其中A∈{4,12,24,32},B∈{9,23,31,33}.根據(jù)引理6及(26)式可得 (27) 由(27)式知僅當B=23時B|23y1,此時y1=1,推出y=2.再由y=v(z-y)即2=v(z-2)可得z=3或4. 當z=3,y=2時,(22)式變?yōu)?76x412(x-3)=1 1053-232=25·3·31·453 371,不可能;當z=4,y=2時,(22)式變?yōu)?76x41x-4=1 1054-232=24·33·5 653·610 501,也不可能. 因此z≡0(mod 2). 若(23)式成立,則對(23)式取模32,有17z≡1(mod 32),得z≡0(mod 2). (ⅱ) 假定方程(3)有適合y>z>x且n>1的正整數(shù)解(x,y,z,n).易知m1=5,m2=2.由(16)式得 23y·41y·3s(y-z)=1 105z-26x. (28) 由(18)式得 23y·41y·2r(y-z)=1 105z-9x. (29) 由(19)式得 23y·41y·2r(y-z)3s(y-z)=1 105z-1. (30) 由定理1知只需證(28)~(30)式中z≡0(mod 2)即可. 若(28)式成立,則對(28)式取模41,有211z≡26x(mod 41),即211z-6x≡1(mod 41).因為2關于模41的階為20,所以2|(11z-6x),可推出z≡0(mod 2). 若(29)式成立,則對(29)式取模8,有(-1)y·2r(y-z)≡0(mod 8),得r(y-z)≥3. 若r(y-z)=3,則對(29)式取模3得-1≡1(mod 3),不可能. 于是r(y-z)≥4. 對(29)式取模16,有1≡9x(mod 16),得x≡0(mod 2).再對(29)式取模41,有211z≡(-25)x≡25x(mod 41),即211z-5x≡1(mod 41).因為2關于模41的階為20,所以2|(11z-5x),可推出z≡0(mod 2). 若(30)式成立,則對(30)式取模41,有211z≡1(mod 41).因為2關于模41的階為20,所以2|11z,可推出z≡0(mod 2). 綜上所述,對任意的正整數(shù)n,方程(3)僅有正整數(shù)解(x,y,z)=(2,2,2). 推論1得證. 致謝:衷心感謝審稿專家提出的寶貴意見!
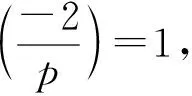
3 推論1的證明