楊勝良, 姜美楊

(蘭州理工大學(xué) 理學(xué)院, 甘肅 蘭州 730050)

樹在組合數(shù)學(xué)中扮演著重要的角色.含有唯一的節(jié)點,使其成為有向樹中其他所有后代的共同祖先,這樣的樹稱作有根樹.若對有根樹每個分支點發(fā)出的邊,按照從左到右(或從右到左)的方向進行標記,稱這樣的有根樹為有序樹.

在有序樹中任意一個頂點到根點的距離叫做這個頂點的層,根點是0層上唯一的點.如果從頂點u到頂點v有一條邊,則稱頂點v為頂點u的孩子,頂點u被稱作v的父頂點,頂點的度數(shù)是其孩子的總數(shù).葉點是度為0的點,即沒有孩子的頂點,出度至少為1的頂點稱作內(nèi)點.當(dāng)樹中只包含葉點時,這樣的樹稱作平凡樹.

d-元樹是有序樹的一種,其中每個頂點的度數(shù)為0或d, 特別地,當(dāng)d=2時,這樣的樹稱作2-元樹.在d-元樹中對每個內(nèi)點用黑色或白色著色,所得的標號樹叫做混合d-元樹.為了與黑色的內(nèi)點進行區(qū)分,用ε標記葉點.在一個混合d-元樹中,稱為邊的一種模式,如果一個內(nèi)點和其最左端的兒子都著黑色.若混合d-元樹中沒有出現(xiàn)該模式的邊,稱為避免模式混合d-元樹.

例1圖1給出有7個內(nèi)點,避免模式的2-元樹.

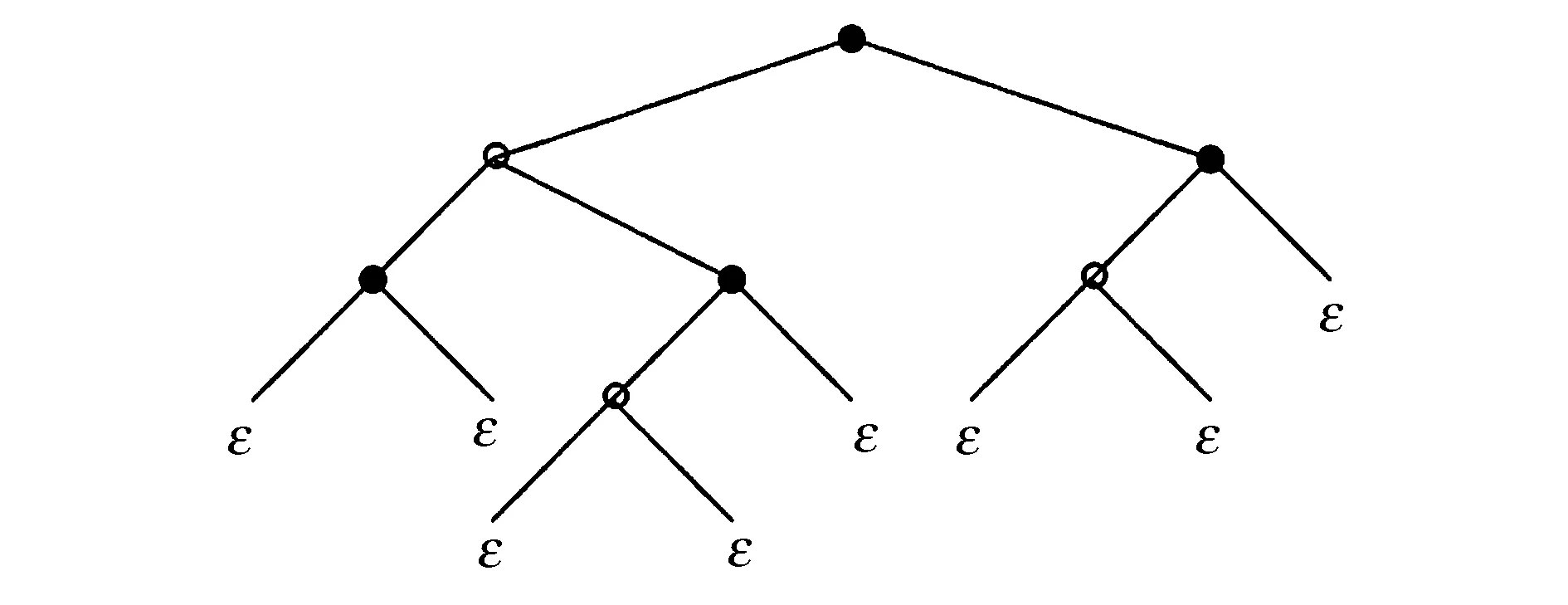
圖1 避免模式混合2元樹

Gu等[1]提出避免模式的2-元樹是混合2-元樹,并考慮了幾類避免其他模式的2-元樹.Panholzer等[2]研究了避免模式的d-元樹,Hong等[3]對混合2-元樹進行了推廣,提出避免模式混合d-元樹,更多相關(guān)研究見文獻[4-6].

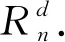
引理1[8](拉格朗日反演公式) 設(shè)f=f(t)是一個由f=tφ(f)定義的形式冪級數(shù),其中φ(t)是一個φ(0)≠0的形式冪級數(shù).對于任何形式的冪級數(shù)F(t)有

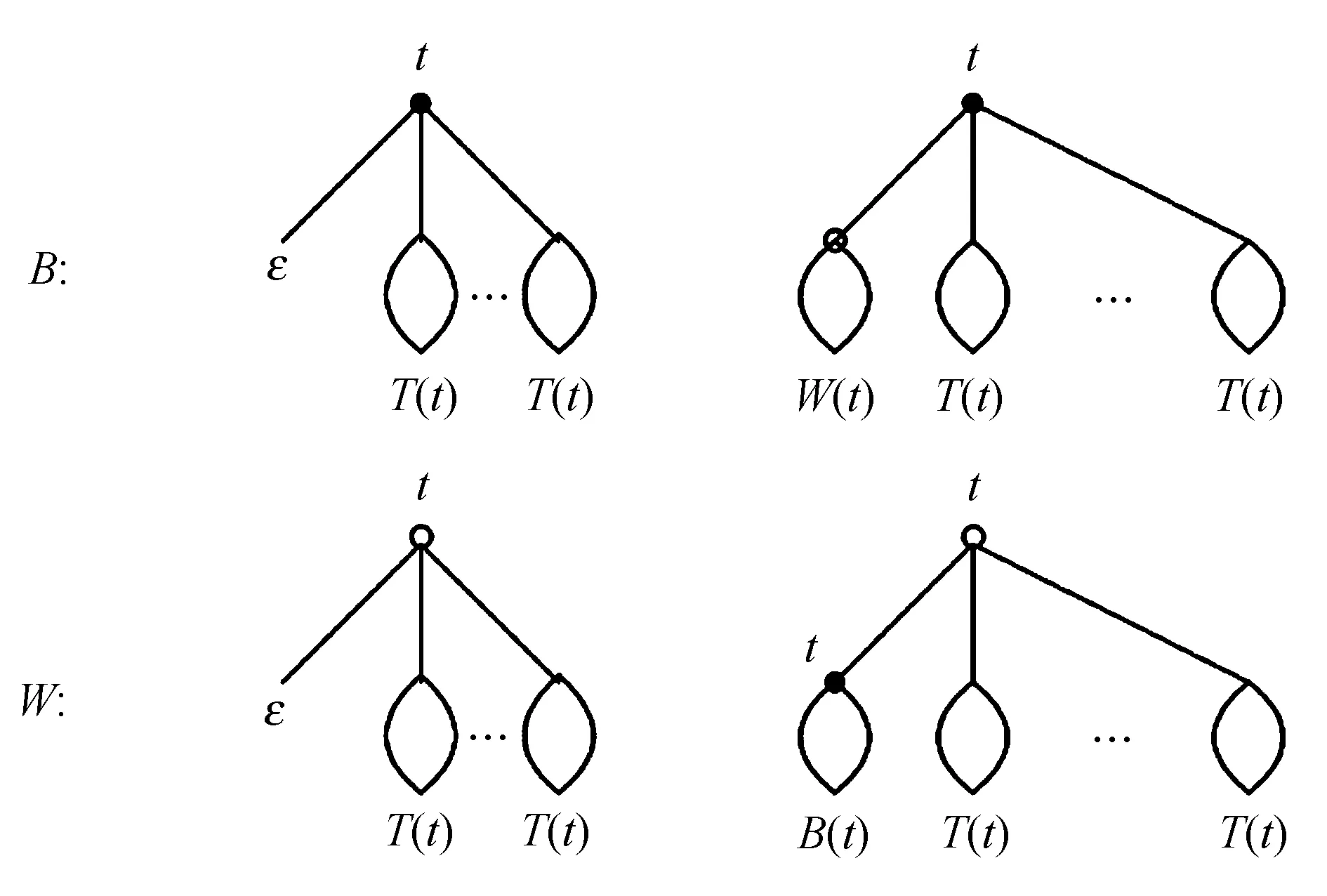
圖2 標記內(nèi)點時避免模式混合d-元樹的分解

設(shè)B(t)為根點是黑色樹的發(fā)生函數(shù),W(t)為根點是白色樹的發(fā)生函數(shù),由圖2可得

所以發(fā)生函數(shù)T(t)為

兩邊同時乘以d-1次方可得

由拉格朗日反演公式得

表的前部分值

證明用t標記內(nèi)點,x標記黑色的內(nèi)點,由符號化方法可以得到圖3的分解.

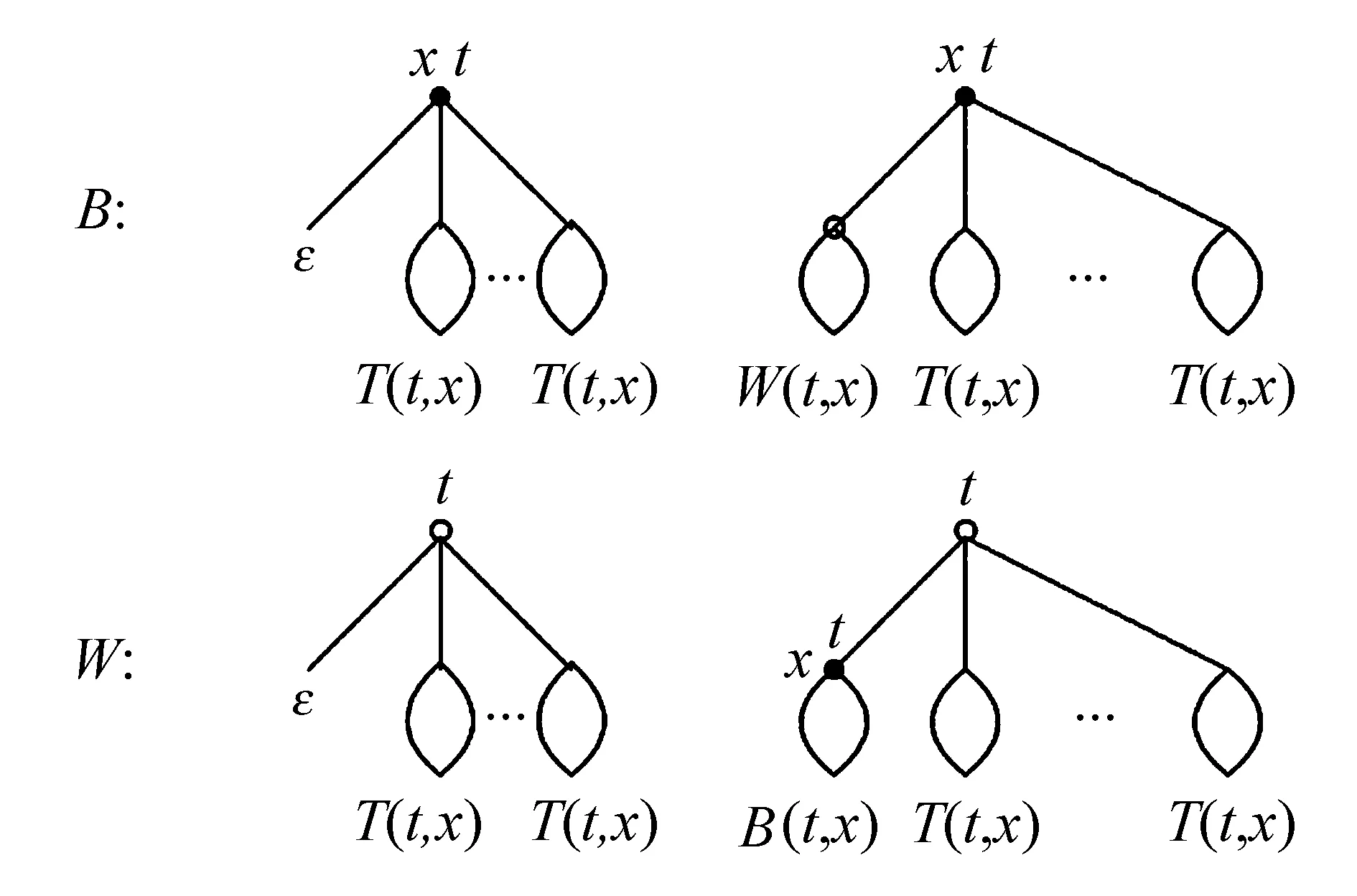
圖3 標記黑色內(nèi)點時避免模式混合d-元樹的分解

設(shè)B(t,x)為根點是黑色樹的發(fā)生函數(shù),W(t,x)為根點是白色樹的發(fā)生函數(shù),由圖3得

B(t,x)=xtT(t,x)d-1+xtT(t,x)d-1W(t,x)

W(t,x)=tT(t,x)d-1+tB(t,x)T(t,x)d-1

B(t,x)=xtT(t,x)d-1+x(1+

B(t,x)(tT(t,x)d-1)2)

W(t,x)=tT(t,x)d-1+x(1+

W(t,x)(tT(t,x)d-1)2)

(1)

(2)

由式(1,2)可得

兩邊同時乘以d-1次方得

設(shè)f(t)=t(T(t,x))d-1, 則

由拉格朗日反演公式得

下面給出雙射的證明.

由圖2易知,W中的任何一個白色根點都有一個最左邊的子樹B和d-1個子樹T1,T2…Td-1.同樣B中的任何一個黑色根點都有一個最左邊的子樹W和d-1個子樹T1,T2,…,Td-1.通過前序遍歷構(gòu)造長度為dn的d-Schr?der路:

1) 訪問一個黑色內(nèi)點時:

(1) 當(dāng)最左邊的子樹為平凡樹時,對應(yīng)于UUT′1UT′2…D(d)T′d-1.

(2) 當(dāng)最左邊的子樹不為平凡樹時, 對應(yīng)于UW′UT′1UT′2…D(d)T′d-1.

2) 訪問一個白色內(nèi)點時:

(1) 當(dāng)最左邊的子樹為平凡樹時,對應(yīng)于UT′1UT′2…H(d)T′d-1;

(2) 當(dāng)最左邊的子樹不為平凡樹時,對應(yīng)于UB′UT′1UT′2…D(d)T′d-1.

3) 對子樹W,B,T1,T2…Td-1繼續(xù)重復(fù)1),2)過程,直到子樹為平凡樹為止.

其中U表示上步(1,1),D(d)表示下步(1,1-d),H(d)表示水平下步(2,2-d)W′,B′,T′1,T′2…T′d-1是W,B,T1,T2…Td-1相對應(yīng)的d-Schr?der路的子集, 該過程也在圖4中給出.

圖4 避免模式混合d-元樹與d-Schr?der路的雙射

由于每個d-元樹經(jīng)過上述分解后所得到的子樹都不相同,故對應(yīng)所得的d-Schr?der路也不同,滿足單射.

圖5 避免模式混合3-元樹與3-Schr?der路的雙射

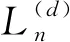
定理4有n個內(nèi)點避免模式混合d-元樹的個數(shù)為

證明用t標記內(nèi)點,x標記黑色的內(nèi)點, 由符號化方法可以得到圖6的分解.

圖6 標記內(nèi)點時避免模式混合d-元樹的分解

由圖5得到發(fā)生函數(shù)為

L(t)=1+tL(t)d-1+t2L(t)2d-1+tL(t)d

化簡可得

兩邊同時乘以d-1次方得

設(shè)f(t)=t(L(t))d-1,

由拉格朗日反演公式得

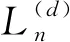
定理5有n個內(nèi)點k個黑色內(nèi)點的避免模式混合d-元樹的個數(shù)為

證明用t標記內(nèi)點,x標記黑色的內(nèi)點,由符號化方法可以得到發(fā)生函數(shù)為

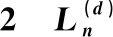
表的前部分值

化簡可得

兩邊同時乘以d-1次方得

由拉格朗日反演公式得

從而得到

例5避免模式混合3-元樹的發(fā)生函數(shù)為L(t,x)=1+xtL(t,x)2+xt2L(t,x)5+tL(t,x)3,具有n個內(nèi)點k個黑色內(nèi)點避免模式混合3-元樹的個數(shù)為

證明用t標記內(nèi)點,由符號化方法可以得到圖7的分解.

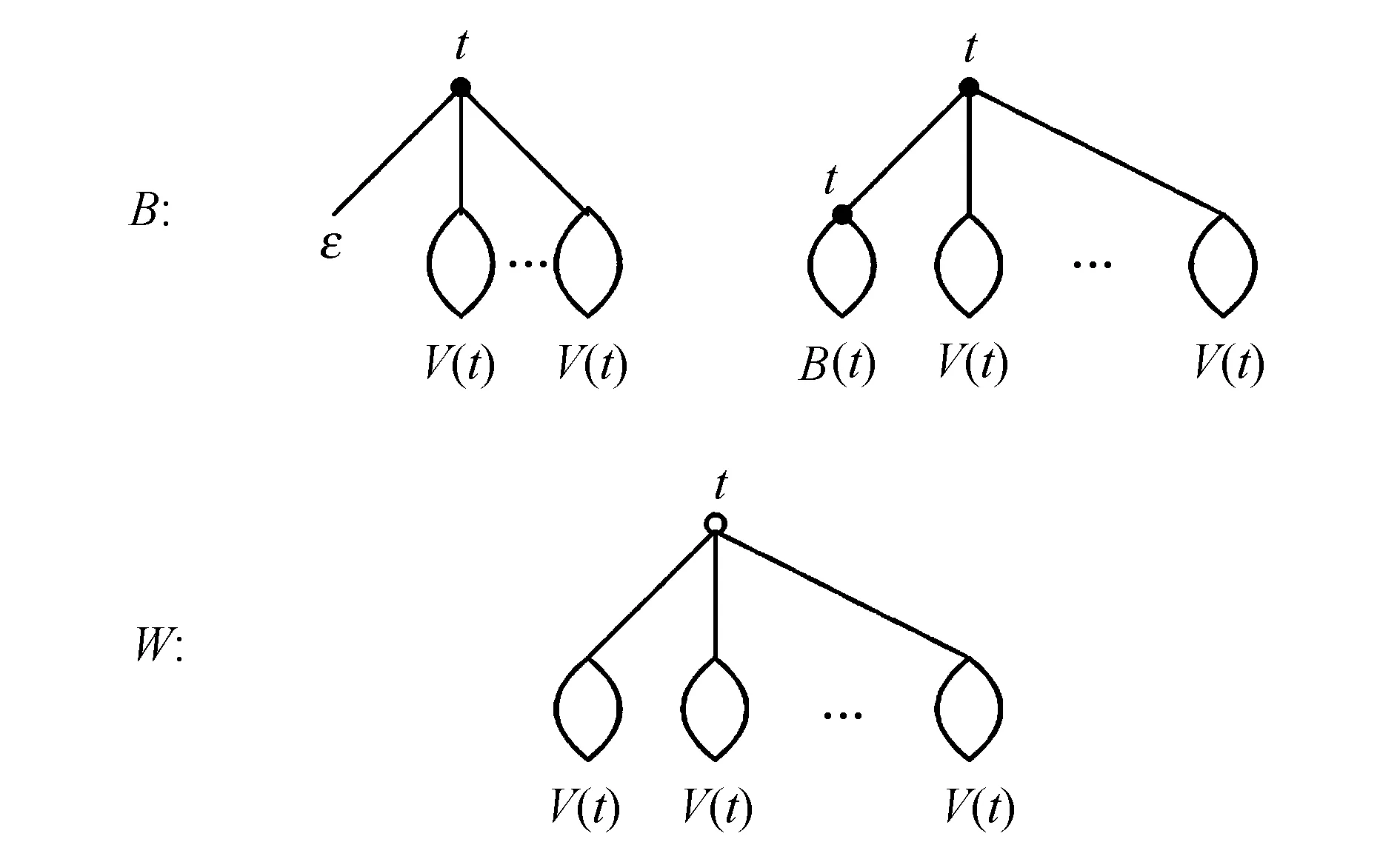
圖7 標記黑色內(nèi)點時避免模式混合d-元樹的分解

設(shè)B(t)為根點是黑色樹的發(fā)生函數(shù),W(t)為根點是白色樹的發(fā)生函數(shù),由圖7可以得到

兩邊同時乘以d-1次方得

由拉格朗日反演公式得

表的前部分值

證明用t標記內(nèi)點,x標記黑色的內(nèi)點,由符號化方法可以得到

可得

兩邊同時乘以d-1次方得

由拉格朗日反演公式得

從而得到