Dynamic Target Enclosing Control Scheme for Multi-Agent Systems via a Signed Graph-Based Approach
Weihao Li,Kaiyu Qin,Mengji Shi,Jingliang Shao,and Boxian Lin
Dear Editor,
This letter investigates the target enclosing control problem of multi-agent systems.A signed graph-based control strategy is presented,where the agents are steered to enclose the dynamic target from both sides as they move.This is inspired by the phenomenon that signed networks exhibit bipartite clustering if the underlying graph is structurally balanced,so that the agents may naturally enclose the zero point from opposite sides (+and ?) if proper controllers are applied.By adopting a distributed observer to estimate the information of dynamic target,a consensus-based enclosing control scheme is designed.Furthermore,a complete Laplacian matrix(CLM)-based Lyapunov analysis method is introduced to prove the control stability,which provides simpler theoretical validation for the stability analysis of average consensus than the conventional method based on state transition matrix.Finally,some numerical simulations are shown to verify the effectiveness of the proposed control scheme.
Networked agents use to require convergence of their states as a part of their cooperation,namely,a consensus reached under properly configured interaction topology and control coefficients [1]–[3].Numerous significant publications have created various collective behavior from extending the consensus algorithm by specifying different placement rules (formation [4]) or information sources (tracking [5],containment [6]),which applies to diverse vehicle group tasks [7]–[9].The analyses of consensus-based system enjoy plenty mathematical tools since the behavior can be simply expressed by convergence of states,while some increasingly demanded multiagent behavior with divergence involved,including area coverage and target enclosing,have not yet been formulated in uniform definitions.Fortunately,target enclosing can be easily exemplified by the scenario of enclosed target(s) being closed off on opposite sides by the agents for diverse purpose like protection,seizure or attack [10].In that sense,several analogous behavior such as surrounding [11],fencing [12] introduced in many past works fall within the scope of“enclosing problems”but expressed in different terms.This also evidences the great value of target enclosing in military surveillance,rescue operation,protection and exploration.
Various ways are found to define the target enclosing problemin literature.Kobayashiet al.[10] describe it as a sub-task of target capturing.Chenet al.[11] formulate the problem with leaders (targets)contained in the convex hull of followers,and specially introduce the concept of symmetric enclosing (“balanced surrounding”) for final configuration of symmetry (in the form of regular-polytope-shaped deployment of the followers whose center overlaps with the leaders’).Target enclosing problems are mainly solved by achieving dynamic formations (with tunable surrounding density depending on the know ledge of targets’ collective motion [11]) or specified deployment in regular shapes (such as the circular/rectangular arrangement[13]) around the target(s).In the final analysis,the agents should be finally deployed on the opposite sides of the target(s) for enclosing.
Different from existing research,this letter comes up with a novel dynamic target enclosing control scheme where the agents are connected by signed networks.Agents may understand neighbors’ information from signed edges in opposite ways,so that their states could eventually diverge in sign (+and ?) to perform enclosing of the zero point (the origin).Specifically,if the signed network is structurally balanced,symmetric enclosing would take place when applying bipartite consensus laws [14]–[17].Inspired by this idea,we develop enclosing control rules in a “consensus”fashion.In our rules,the stationary is replaced by traveling target whose data is processed in the signed network,so that the agents will symmetrically move between the two sides of the enclosed target at last.The contributions of this letter include: 1) A novel signed graph-based dynamic target enclosing control scheme is proposed.The consensus-based control algorithm is designed utilizing the natural bipartite clustering phenomena in structurally balanced networks to create divergence of agents around a target.This strategy extends the methodology for dynamic target enclosing problems,and can be generalized to numerous applications by bringing formation control or coordinate transformation into the algorithm.2) This article has also designed an efficient approach to stability proof of consensus-based algorithms by constructing a CLM ? the Laplacian matrix of a normalized complete graph that shares the same node partition as that of the original signed networks.With the help of several properties of CLM,target enclosing among networked agents can be conveniently validated in theory,which is simpler than the conventional method based on state transition matrix.
Preliminary and problem formulation:In this part,we will first introduce some relevant basics of graph for network connection and useful lemmas.Then,the target enclosing problem is formulated.
In this letter,an undirected signed graph G={V,E} is adopted to denote the communication topology among the multi-agent system,where the set of agents is V={ ν1, ν2,..., νn},and the set of links is E ?V×V .The valueai jof matrixA=[ai j]∈Rn×nrepresents the information exchange between the agentiand agentj.Then,the Laplacian matrixLis defined asL=H?A,whereH∈Rn×nis the weighted degree matrix andH=diag{h1,h2,...,hn},hi=Without loss of generality,a signed graph G is structurally balanced if there exists a bipartition V1,V2of the nodes with V1∪V2=V and V1∩V2=?,such thatai j≥0 when νi, νjare in the same subgroup,andai j≤0 when νiand νjare in different subgroups.Thus,for a structurally balanced graph,denote W=(w1,w2,...,wn)T∈Rn×1as a signature matrix,wherewi=1 if νi∈V1andwi=?1 if νi∈V2.
Lemma 1: Consider a connected undirected graph withnnodes whose Laplacian matrixLhas a single zero eigenvalue and the corresponding eigenvector is W.In other words,Lis semi-positive definite,andLW=(WT L)T=0n×1.
To provide simpler theoretical validation for the stability analysis,a special Laplacian matrixC∈Rn×n(called CLM) which shares the same node partition as that of the original signed networks is defined,whereandInis a identity matrix.Obviously,
Lemma 2: IfC,Lare the CLM and Laplacian matrix of a normalized complete graphand connected graph G,respectively.The following propositions hold.
which indicates that all the eigenvalues of (L+WWT) are positive.That means (L+WWT) is positive definite.Furthermore,(L+WWT)C=LC+W(CW)T=LC,then the proof of the second proposition is achieved.
Considering a first-order multi-agent system,whose model dynamics can be described asi∈I,wherexianduidenote the position and control input of agenti,respectively.The index set is I=(1,2,...,n).To describe the target enclosing problem of the multi-agent system,we first define the position of moving target isx0,which is generated by an external reference system with provided system in formation:where ? is the state of external reference system,are the system matrix and output matrix,respectively.In this letter,only the position of target is accessible to informed agents.
Definition 1 (Target enclosing problem): The control lawuiis applied to achieve target enclosing,if the states of multi-agent systems finally satisfy l imt→∞|xi?sgn(ai j)xj+(sgn(aij)?1)x0|=0.
Foriandj-th agents which in the same sub-graph,i.e.,a i j>0,one sees their convergence (xi(t)→xj(t)) ast→∞,while for two agent in different sub-graph,i.e.,aij<0,then they will finally be evenly located on the two sides of the targetx0,that is,(xi(t)?x0(t))→?(xj(t)?x0(t)) ast→∞.In other words,the agents will be deployed to enclose the moving target and keep it as their geometry center.According to the Definition 1,the enclosing error is defined as
The main objective is to design the target enclosing control protocol for agents.
Main results:This part provides solutions to the target enclosing problems.The controller is produced by constructing a distributed observer to estimate the state of target for each agent.The target information is generated by the external reference system,and the following assumptions are made throughout this part.
Assumption 1: The system matrixAξand output matrixCξare available for each agent.The target can be regarded as a virtual leader for the multi-agent system,and we define the communication matrix between agents and target is Γ=diag{Γ1,Γ2,...,Γn}∈Rn×n,if agentican measure the target’s information,Γi>0,otherwise Γi=0.At least,one agent can measure the information of target,that is?i,Γi>0.
In order to realize the distributed observation of moving target among the topology network,the estimation information of the agent to external reference system is defined as,and the observed value of the target isFurthermore,the distributed observation errors can be defined asThe distributed observer is further constructed as
Then,the control input is designed as
wherek>0 is the controller gain.
Theorem1: By adopting the control input (4),if the Assumption 1 and Lemma 3 are hold,the target enclosing of multi-agent systems is achieved.
Numerical example:In this part,some simulation results are given to verify the effectiveness of the proposed control scheme.Fig.1(a) shows the topology among the agents,and the symbol matrix.Moreover,consider that only 1st agent can measure/receive the state informationx0of target,thus the weight matrix is Γ=diag{1,0,0,0}.The system and output matrices of external reference system are
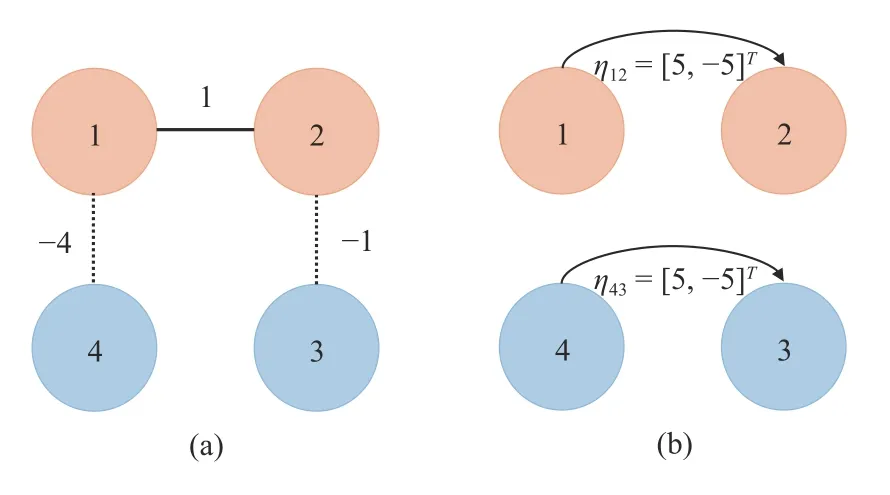
Fig.1.The interactions among the agents.(a) The topology among the agents;(b) The formation of agents.
It follows that,foriandj-th agents which in the same sub-graph,theirx-axis states deviation finally approach to (xix?xjx)= ηxi j,while for the two agents in different sub-graph,that is,(xix+xjx)=2x0x.The formation interval ηijbetween agentiandjis shown in Fig.1(b),where ηxi j=? ηx ji.The simulation result is shown in Fig.2.Eventually,each agent moves in different circle,and their formation surrounds the target.
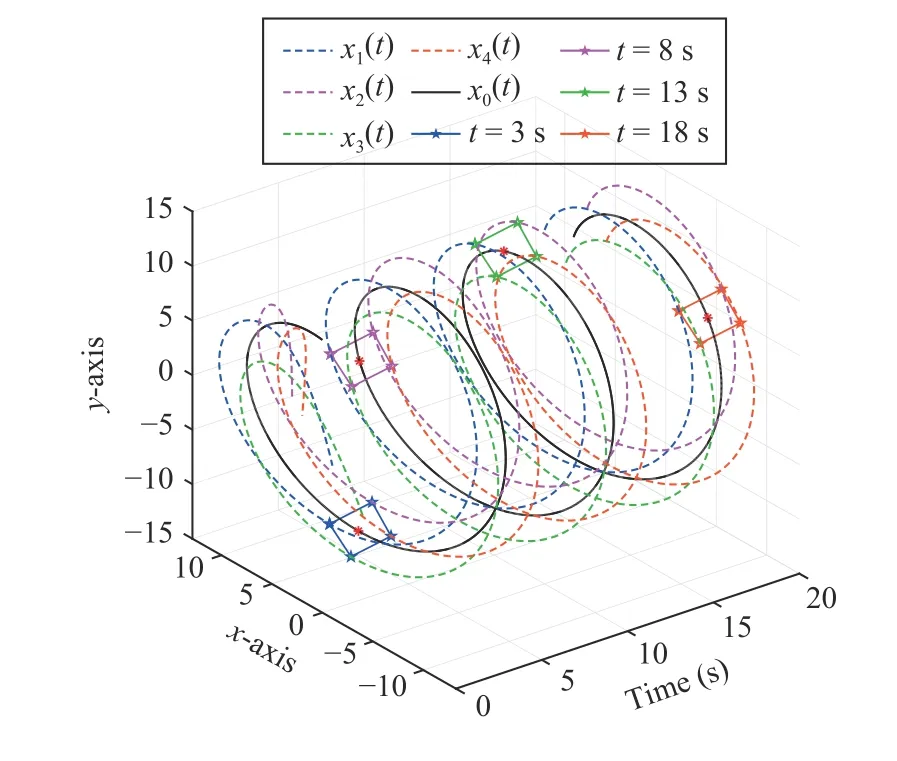
Fig.2.The positions of agents and target in three-dimensions (circular motion).
Conclusion:This letter investigates the target enclosing control problem of multi-agent systems,different from the existing methods in literature,a novel distributed signed graph-based control scheme is proposed.The dynamic target enclosing control is completed by designing an distributed observer for the moving center of the signed network to achieve enclosing tracking around the target.Moreover,a CLM,the Laplacian matrix of a normalized complete graph which shares the same node partition as that of the original signed networks,is constructed to prove the closed-loop stability of system.In future work,we may focus on the extension of the proposed signed graphbased to the target(s) enclosing problem in real-world applications,such as protection,seizure or attack for military operations.
Acknowledgments:This work was supported by the Science &Technology Department of Sichuan Province (2022NSFSC0037,2022JDR0107,2020YJ0044,2021YFG0131),the Fundamental Research Funds for the Central Universities (ZYGX2020J020) and the National Numerical Wind Tunnel Project,China (NNW 2021 ZT6-A26).
 IEEE/CAA Journal of Automatica Sinica2023年2期
IEEE/CAA Journal of Automatica Sinica2023年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- The Distribution of Zeros of Quasi-Polynomials
- Straight-Path Following and Formation Control of USVs Using Distributed Deep Reinforcement Learning and Adaptive Neural Network
- Prescribed-Time Stabilization of Singularly Perturbed Systems
- Visual Feedback Disturbance Rejection Control for an Amphibious Bionic Stingray Under Actuator Saturation
- Optimal Formation Control for Second-Order Multi-Agent Systems With Obstacle Avoidance
- CoRE: Constrained Robustness Evaluation of Machine Learning-Based Stability Assessment for Power Systems
