CoRE: Constrained Robustness Evaluation of Machine Learning-Based Stability Assessment for Power Systems
Zhenyong Zhang and David K.Y.Yau,
Dear Editor,
Machine learning (ML) approaches have been widely employed to enable real-time ML-based stability assessment (MLSA) of largescale automated electricity grids.However,the vulnerability of MLSA to malicious cyber-attacks may lead to wrong decisions in operating the physical grid if its resilience properties are not well understood before deployment.Unlike adversarial ML in prior domains such as image processing,specific constraints of power systems that the attacker must obey in constructing adversarial samples require new research on MLSA vulnerability analysis for power systems.In this letter,we propose a novel evaluation framework to analyze the robustness of MLSA against adversarial samples with key considerations for damage (i.e.,the ability of the adversarial data to cause ML misclassification),bad data detection,physical consistency,and limited attacker’s capacity to corrupt data.Extensive experiments are conducted to evaluate the robustness of MLSA under different settings.
To achieve comprehensive context awareness of power systems integrated with renewable energy sources,household loads,and electric vehicles,inter net of things (IoT) technologies have been widely integrated into power systems to enable autonomous monitoring,optimization,and control.However,the increasing complexity of the power system necessitates ever more complicated,if not outright infeasible,models for traditional analytical methods to achieve sufficient coverage and accuracy,which brings challenges to efficient and agile system operations.To address the problem,big data collected by IoT monitoring devices may allow data-driven ML approaches to control/optimize the power system’s operation effectively.As a typical example,MLSA has been widely used to assess/predict whether the current operating condition (OC) of an electrical grid is system wide stable or unstable subject to credible contingencies in real-time[1].It enables the grid to operate close to its stability limits in meeting significantly fluctuating demand,frequent kicks-in and out of intermittent energy resources,extreme weather conditions,etc.On the other hand,a host of real-world incidents,such as Black Energy and Stuxnet among others [2],evidence that communication channels supporting the IoT are prone to attacks by malicious cyber actors[3] and [4].
Meanwhile,research has shown that ML models can be generally misled by adversarial samples to give wrong answers [5].Interestingly,adversarial samples investigated for computer vision,due to their low energy,are found to escape notice completely by the human eye while fooling the ML.For example,a cat image,with only a single pixel strategically subverted,can be misclassified as a dog.As a result,the robustness of ML models and their verification [6] under adversarial scenarios has attracted a lot of attention.This robustness metric can play a major role in selecting the best ML models for specific applications.However,traditional robustness analysis is not suitable for power grids [7].Venzke and Chatzirasileiadis [8] analyzed the robustness of a fully connected neural network trained for security assessment by formulating it as a mixed-integer linear programming problem.Ren and Xu [9] analyzed the robustness of MLSA under different norms and verified lower bounds of adversarial perturbations.Their results do not consider key power-domain properties,however.
To have real impacts in the power domain,adversarial samples must obey its constraints or they will fail to mislead the MLSA into wrong decisions.This letter addresses this key requirement that has not been well addressed in the state of the art.
Specifically,this letter considers the adversarial scenario shown in Fig.1.Control centers usually adopt security measures such as airgapped isolation or logical isolation by a virtual private network(VPN).We assume that the attacker uses pathways like compromised USB drives or existing VPN intrusions to subvert the MLSA by modifying data (e.g.,sensor measurements) in the local supervisory control and data acquisition (SCADA) network.This data may be assessed for integrity before being used by the MLSA,e.g.,a bad data detection (BDD) method in state estimation can be used to reject abnormal data.Hence,we require adversarial samples to bypass the BDD before they can do damage.Besides,the adversarial examples must be credible data that meets physical constraints like power balance and power limits.Lastly,it is assumed that the attacker will not be able to corrupt certain data due to limited capability or other available defenses in the system.Note that prior work [10] has advanced an approach to evaluate MLSA robustness considering physical constraints under a linearized dc model.However,it has not addressed the security of MLSA under a nonlinear ac model.To address the gap,we propose a constrained robustness evaluation (CoRE) framework that analyzes MLSA robustness under an ac model in the face of attacks that satisfy a set of practical constraints including effectiveness (to cause misclassification),BDD bypass,physical consistency,and attacker’s limited data corruption capability.We also present extensive experiments to analyze the robustness of MLSA under different ML models and model parameters.
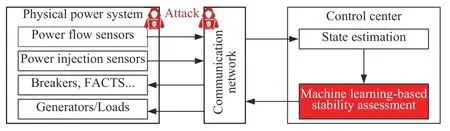
Fig.1.Adversarial scenario of the MLSA.We assume that the field sensors and communication networks are vulnerable to cyber-attacks that compromise data integrity [2].
Problem formulation:
MLSA: Use of data-driven MLSA,supported by a control center with suitable computational and storage servers,is gaining interest among researchers and utility operators [11].Such MLSA works as follows.It consists of two main stages: offline training and online prediction.First,detailed numerical stability analysis is conducted for a variety of OCs under different contingencies.The stability vs.instability of the OCs labels each corresponding data point.The training dataset is denoted byS={s1,s2,...,s N},wheres i={z i,yi} fori∈{1,2,...,N};z iis an OC;andyi=0 or 1,where “0”stands for“unstable”and “1”for “stable”.In general,an OC is driven by power data such as power injections,power flows,and voltage phasor quantities.The off line training is carried out with the labeled training dataset to learn an optimized MLSA modelf,whereas,in the online prediction stage,the current OCz iis fed as real-time input to the MLSA model,which then determines if the OC is stable or not.In this letter,we mainly analyze the vulnerability of the prediction process of MLSA.
For ease of illustration,we use linear classifiers for the stability assessment in the following.We consider a binary classifier (a general multi-class classifier can be treated as an aggregation of binary classifiers),so that the MLSA model output has two possible values,namely=M(z i)=sign(f(z i)),where sign(·) is a sign function:M(z i)=1 iff(z i)>0 and M(z i)=?1 iff(z i)≤0.Unlike adversarial analysis in other domains such as computer vision,we postulate detection and mitigation mechanisms for rejecting bad data in the training and testing phases of the MLSA.Therefore,adversarial samples must be able to bypass these defenses before they can compromise the MLSA results.
CoRE framework:We propose a CoRE framework for MLSA models.An adversarial sample of a specificz imust satisfy the following constraints:
1) Misclassification constraint (C1): The adversarial sample needs to cause a wrong ML prediction with respect to the ground truth,i.e.,
2) Consistency constraint (C2): As discussed,effective adversarial samples cannot violate physical consistency such as power balance and limits for generation,loads,power flows,etc.Power balance will be maintained if the BDD constraint (i.e.,C3) is satisfied.To meet the power limit constraint,the adversarial perturbation should satisfy
where?mminand ?mmaxare respectively the lower and upper limits of the adversarial perturbation on the measurement.
3) BDD constraint (C3): Here,the spatial mutual dependency of power data is considered.The adversarial perturbations need to bypass the BDD that filters out bad data.According to [12],the BDD is circumvented through
4) Corruption constraint (C4): Unlike other domains such as computer vision,inputs to the MLSA model may not be easily observed or corrupted if the power system in question is not fully open.The traditional adversarial assumption that the attacker has good know ledge of inputs to the ML model may not hold in the context of power systems,e.g.,certain measurements are not known because there are no available physical and cyber channels for the attacker to access the data.Suppose the set of such data is denoted by P.Then,the corruption constraint is defined by
Overall,the robustness of MLSA for a specific OCz iis evaluated by solving the following problem:
where the operation ∥·∥ can be the ?0,?1,?2,and ?∞norm.We can see that the minimization problem is nonlinear and nonconvex.Thefminconpackage,a nonlinear optimizer in MATLAB,is adopted to compute the optimal solution.Overall,the RoCE of an MLSA modelfis defined as
whereTis the number of test OCs.The RoCE framework for MLSA models is given in Fig.2.
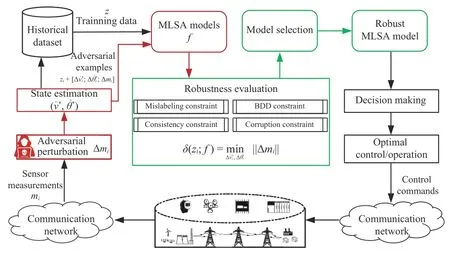
Fig.2.The constrained robustness evaluation framework for MLSA models.
Experimental results:We conduct experiments based on an IEEE 68-bus power system[13],which consists of 68 buses,83 transmission lines,and 16 generators.For diversity,the active loads are obtained by sampling from a multivariate Gaussian distribution with a Monte Carlo method.The nonlinear ac model is considered to calculate active and reactive power injections and power flows.
The transient stability of generators is analyzed to generate the dataset.The stability is violated if the difference between any phase angles of generators is larger than 180?at any point in time during the simulation period.We create four different three-phase line outages,corresponding to t he branches {63,62},{59,58},{25,54},{31,30},respectively,to act as contingencies,denoted byCT1,CT2,CT3,andCT4.Each contingency lasts for 10 s.For each contingency,a total of 12 000 OCs are collected,in which 10 000 samples are used for training and 2000 samples for testing.
The MLSA is implemented with the support vector machine(SVM).The overall robustness (11) is computed with 10000 OCs.The robustness value ξadv(f) is calculated as an ?2norm.According to our analysis,it is possible for the RoCE problem(10) to not have any feasible solution,which means that the adversarial perturbation violates one or more of the constraints (C1,C2,C3,or C4).Therefore,we define an additional metric to quantify the robustness of MLSA models ξ roc(f)=#of robust OCs/#of test OCs,where a robust OC is one that does not have feasible adversarial perturbations according to Problem(10).Note that the value of ξroc(f) is the ratio of robustness OCs among all test OCs.
First of all,the robustness of RoCE is evaluated for MLSA under different contingencies.Here the penalty factor for the SVM model is fixed to 10.We randomly select 8 measurements that cannot be corrupted for each adversarial example.Datasets of the four contingenciesCT1,CT2,CT3,andCT4are used.Table 1 shows the evaluation results.We find that the robustness of MLSA increases when more constraints are added to the optimization Problem(10) under the contingenciesCT1,CT2,andCT4.Although the robustness metric ξadv(f) with the constraints C1∧C2∧C3∧C4is smaller than that with the constraints C1∧C2∧C3under the contingencyCT3,the robustness metric ξroc(f) with the former constraints is larger than that with the latter constraints.We believe that this result is obtained because the measurements that cannot be corrupted are far away from the classification boundary.
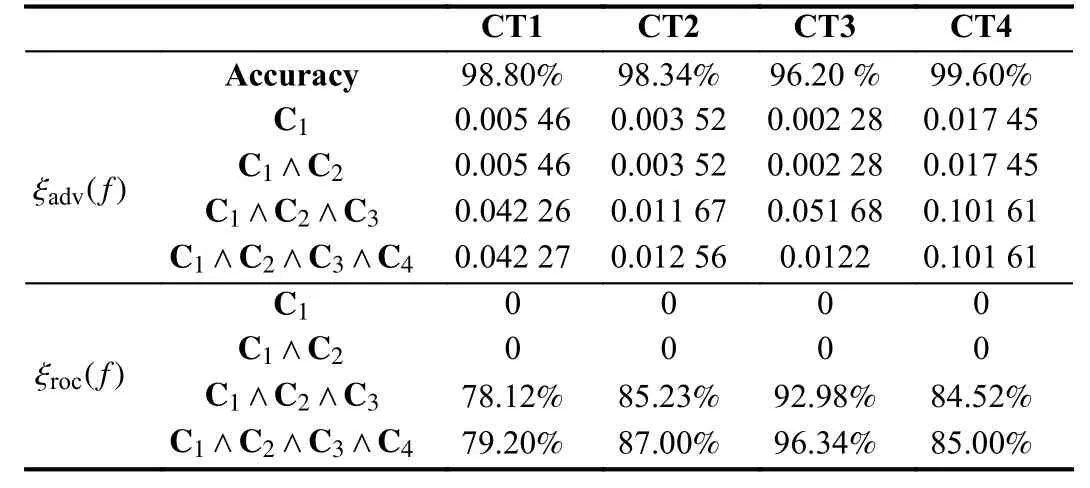
Table 1.Robustness of Mlsa Across 4 Contingencies Under Different Constrai nts.“ ∧”Means “and”
Besides,from Table 1,it seems that the BDD constraint increases the value of ξadv(f) by several times (e.g.,8,3,20,9 times of that with constraints underCT1,CT2,CT3,andCT4,respec-C1 ∧C2tively).Since BDD is widely used in power systems,attackers face increased difficulty in constructing effective adversarial samples in practice.Table 1 also presents the number of robust OCs as the value ξroc(f).It appears that the BDD and corruption constraints can reduce the attacker’s ability to construct successful adversarial samples by 80%,which implies that the defenses can reject most of the adversarial samples.
Different from the prior work [10],we also analyze the impact of the corruption constraint (i.e.,C4) on the values of ξadv(f) and ξroc(f).The penalty factor of SVMis fixed to 10.The dataset for the contingencyCT2is used.Al l constraints C1,C2,C3,and C4are considered.A set of experiments are conducted by varying the set of measurements that cannot be corrupted.In Table 2,PM 1,PM 2,PM 3,andPM 4mean that there are respectively 10,8,5,and 3 randomly selected measurements that cannot be corrupted for each adversarial sample.We find that the val ues of ξadv(f) and ξroc(f)increase when there are more protected measurements,which indicates that the robustness of MLSA can be enhanced by the conventional wisdom of protecting critical measurements.

Table 2.Robustness of Mlsa Emphasizing on the Corruption Constraint (i.e.,C4)
We further evaluate the robustness of MLSA with different SVM parameters.The contingencyCT2is used as an example and there are 8 measurements randomly selected that cannot be corrupted for each adversarial sample.From Table 3,the robustness ξadv(f) of MLSA withPF(penalty factor)=0.1 is the largest,whereas the robustness is the highest withPF=1 according to the metric ξroc(f).The robustness ξadv(f) seems t o decrease when the accuracy of the SVM model increases.It seems that the robustness of MLSA is affected by the model parameter,which should be carefully set considering the security issue.
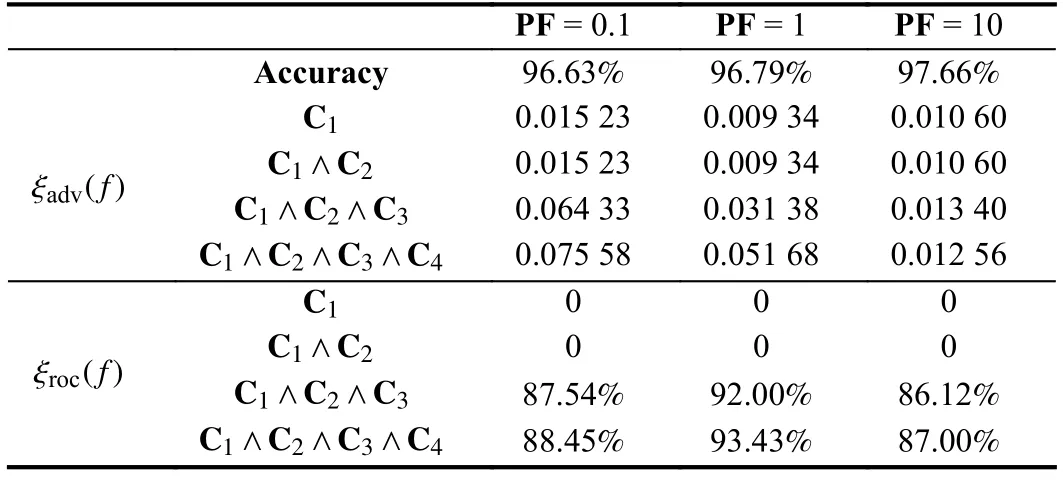
Table 3.Robustness of Mlsa With Different Penalty Factors (PF)
Acknowledgments:This work was supported in part by the Guizhou Provincial Science and Technology Projects (ZK[2022]149),the Special Foundation of Guizhou University (GZU) ([2021]47),the Guizhou Provincial Research Project for Universities([2022]104),the GZU cultivation project of the National Natural Science Foundation of China ([2020]80),and Shanghai Engineering Research Center of Big Data Management.
 IEEE/CAA Journal of Automatica Sinica2023年2期
IEEE/CAA Journal of Automatica Sinica2023年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- The Distribution of Zeros of Quasi-Polynomials
- Straight-Path Following and Formation Control of USVs Using Distributed Deep Reinforcement Learning and Adaptive Neural Network
- Prescribed-Time Stabilization of Singularly Perturbed Systems
- Visual Feedback Disturbance Rejection Control for an Amphibious Bionic Stingray Under Actuator Saturation
- Optimal Formation Control for Second-Order Multi-Agent Systems With Obstacle Avoidance
- Dynamic Target Enclosing Control Scheme for Multi-Agent Systems via a Signed Graph-Based Approach
