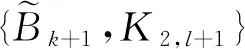周金秀, 王文環(huán)

(上海大學(xué) 數(shù)學(xué)系, 上海 200444)

本文考慮的圖都是無向且無重邊的簡單連通圖.設(shè)H=(V(H),E(H))是具有n個(gè)頂點(diǎn)的圖,其中V(H)和E(H)分別是圖H的頂點(diǎn)集和邊集.圖H中一個(gè)頂點(diǎn)的度定義為圖H中與這個(gè)頂點(diǎn)關(guān)聯(lián)的邊條數(shù).如果H的所有頂點(diǎn)都具有相同的度k,那么稱H是k-正則的,其中k≥1.一個(gè)k-正則圖H稱為(k,a,c)強(qiáng)正則的,當(dāng)且僅當(dāng)H中每對相鄰的頂點(diǎn)都有a≥0個(gè)公共鄰居,每對不相鄰的頂點(diǎn)都有c≥1個(gè)公共鄰居.令A(yù)(H)和D(H)分別是圖H的鄰接矩陣和度對角矩陣.對于任意0≤α≤1, Nikiforov[1]提出研究A(H)和D(H)的凸線性組合Aα(H)矩陣,且將其定義為:

Aα(H)=αD(H)+(1-α)A(H).

圖H的α-譜半徑,記為ρα(H),其定義為Aα(H)所有特征值中的最大值.

如果0≤α<1且H連通,那么Aα(H)是不可約的.根據(jù)Perron-Frobenius定理,它具有唯一的單位正特征向量x=(x1,x2,…,xn)T與ρα(H)相對應(yīng).我們稱這個(gè)向量x為H的α-Perron向量[1].令di是圖H中第i個(gè)頂點(diǎn)的度,其中1≤i≤n.有

(1)

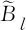
Brualdi和Hoffman[2]提出了譜Turán型極值問題:在不包含給定子圖的圖類中,研究譜半徑的最值問題,并刻畫取得極值譜半徑的極值圖.譜Turán型極值問題是圖譜理論中一個(gè)重要且有趣的問題,吸引了很多學(xué)者的關(guān)注,人們獲得了豐富的研究成果,對其詳細(xì)了解,可參見綜述文獻(xiàn)[3-5].下面,本文重點(diǎn)闡述當(dāng)禁用子圖為Bl和Ks,t的譜Turán型極值問題的研究進(jìn)展.

2007年,Nikiforov[6]在禁用{Bk+1,K2,l+1}的簡單圖中,得到了譜半徑的上界.2007年,Shi和Song[7]在禁用{Bk+1,K2,l+1}的簡單圖中,刻畫了具有最大譜半徑的極值圖.2009年,Babai和Guiduli[8]在禁用Ks,t的簡單圖中,證明了此類圖譜半徑的上界.2010年,Nikiforov[9]使用不同方法改進(jìn)了Babai和Guiduli[8]的結(jié)果.2016年,De Freitas等[10]在禁用K2,s+1的簡單圖中,得到了具有最大無符號拉普拉斯譜半徑的上界,并刻畫了達(dá)到上界的極值圖.2017年,Kong和Wang[11]不僅在禁用Ks,t的簡單圖中,給出了無符號拉普拉斯譜半徑的上界,而且在禁用{Bk+1,K2,l+1}的簡單圖中,得到了無符號拉普拉斯譜半徑的上界,并刻畫了達(dá)到上界的極值圖.

1 主要結(jié)果

為了得到本文的主要結(jié)果,下面引入引理1和引理2.

引理1設(shè)H是具有n個(gè)頂點(diǎn)且最大度為Δ的連通圖.則

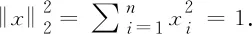
ρα(H)=xTAα(H)x

≤αΔ+(1-α)(xTA(Kn)x-2∑vivj?E(H)xixj)

≤αΔ+(1-α)(n-1)-2(1-α)∑vivj?E(H)xixj.

上式經(jīng)過整理,得到引理1.

引理2設(shè)H是具有n個(gè)頂點(diǎn)且最大度為Δ的連通圖.則

證明令x=(x1,x2,…,xn)T是H的α-Perron向量.則

ρα(H)=xTAα(H)x

下面給出本文的主要結(jié)果定理1.

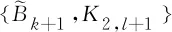
等號成立當(dāng)且僅當(dāng)H是頂點(diǎn)數(shù)為n的完全圖,且Δ=n-1,2k=n-2,l=0.

≤2k∑vpvq∈E(H)xpxq+l∑vpvq?E(H)xpxq.

(2)

根據(jù)Aα(H)x=ρα(H)x,有

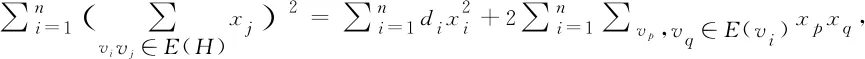
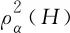
由于[2αΔ+2(1-α)k]α+[-α2Δ-2α(1-α)k+(1-α)2]=α2Δ+(1-α)2,上式可化為

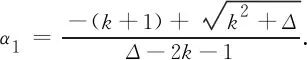
(3)

令[2αΔ+2(1-α)k]+f(α)-(1-α)l=(2k+1-Δ)α2+(2Δ+l-4k-2)α+2k+1-l=P.令Q=4(1-α)l[αΔ+(1-α)(n-1)].經(jīng)過整理,(3)式可化為

(4)

由(4)式,可以推出

(5)

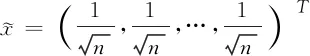
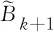
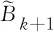
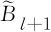
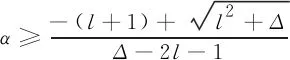
2 結(jié)束語