Online Parallel-Batch Machines Scheduling with a Single Server
(1.School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China;2.Institute of Technology and Standards Research,China Academy of Information and Communication Technology,Beijing 100191,China;3.Key Laboratory of Internet of Vehicle Technical Innovation and Testing (CAICT),Ministry of Industry and Information Technology,Beijing 100191,China.)
Abstract: We consider parallel-batch machines scheduling problem with a single server to minimize the maximum completion time.Jobs arrive over time.Every batch has to be loaded by the sever before being processed on machines.The loading (setup) operation of a batch occurs only when some machine is idle,and the server can perform only one setup operation every time.For some special case,we provide a best possible online algorithm with competitive ratio (+1)/2. For general case,we give another online algorithm with competitive ratio 3.
Keywords: Parallel-batch machines;Server;Online algorithm;Competitive ratio
§1.Introduction
Parallel batch scheduling with a single server is generally applied in industrial automation field,where scheduling workers need to move processing materials to machines.In recent years,China and other countries in the world are vigorously developing intelligent transportation,V2X(vehicle to everything) has been strategically deployed.V2X enables information interaction between vehicle to vehicle and vehicle to infrastructure,which can significantly improve traffic safety and efficiency.V2X communication has high requirement on delay and reliability,which has also put forward high requirement on processing capacity of application data (see Wang et al.[7]).In a real deployment,a mobile edge computing server might rent computing resources from multiple companies.After receiving computing tasks that arrive online from vehicles or road-side infrastructures,the mobile edge computing server needs to determine when to batch which computing tasks up to the idle computing resources to minimize the cost of renting the computing resources.Assume that the cost ofm-home computing resources rented by the mobile edge computing server is only related to the last term,to minimize the rental cost is to minimize the completion time of all computing tasks.The mobile edge computing server can upload multiple computing tasks to computing resources in batches at the same time,and the uploading time of this batch of computing tasks is the uploading time of the computing task with the largest amount of data in this batch of computing tasks.Each computing resource can accept new computing tasks when it is idle,and can simultaneously process batch computing tasks,with the computing task processing time equal to the computing task requiring the longest processing time.In the above deployment scenario,the processing of the moving edge computing server can be modeled as the following scheduling model: parallel-batch machines with a single server under online setting,the objective is to minimize the makespan.
In this online scheduling problem,there aremmachines,M1,M2,···,Mm,andnjobs(wherenis not known in advance),J1,J2,···,Jn,to be processed on machines.JobJjhas arrival timerj,setup timesjand processing timepj.The jobs arrive over time where no information is known about any future jobs,and a job must be loaded by the server on one machine before to be processed.The loading time is also called setup time.The setup operation of a job (batch)occurs only when some machine is idle,and the server can perform only one setup operation every time.The single server is just like a porter or a robot,who carries one job (or batch) to an idle machine before the time when the machine starts to process the job (or batch).While cost,physical space limitations and the need to simplify the production process may be the reasons for the use of only a single server.In this model,the sever can load a batch on to machines every time and we suppose that the capacity of a batch is infinite.The setup time and processing time of a batch equal the largest setup time and the largest processing time,respectively,of jobs in the batch.We denote the problem byPm,S|online,rj,p-batch,b∞|Cmax.
The quality of an online algorithm is often assessed by evaluating its competitive ratio.For any instance,if the objective value of a schedule produced by the online algorithm is no more thanρtimes the optimal offline objective value,we call the algorithm isρ-competitive.An online algorithm is optimal if no smaller competitive ratioρcan be established for this problem.
Parallel-batch machines scheduling problem with a single server is rarely studied,but many works have been done about identical machines scheduling problem with a single server.Formidentical machines with a single server,under assumptions about processing times and setup times,Hall et al.[2] provided varieties results for a number of classical scheduling objectives.They mainly provided either a polynomial-or pseudo-polynomial-time algorithm,or a proof of binary or unary NP-completeness.The objective value of the following references is to minimize makespan.Kravchenko and Werner [5] considered parallel machine scheduling problems with a single server.They first proved that the problem is NP-hard even for two machines and then presented a pseudo-polynomial algorithm for the case of two machines when all setup times are equal to one.Besides,they proved that the more general problem with an arbitrary number of machines is unary NP-hard and analyzed some list scheduling heuristics for this problem.For preemptive scheduling on two parallel machines with a sever,Jiang et al.[3]presented an algorithm with a tight bound of 4/3 for the general case.For two special case: equal processing times and equal setup times,they proved that the above algorithm can produced optimal schedule.For online scheduling problem with a single server,Zhang [8] considered the problem on two identical machines under online over list setting,they proved that list scheduling algorithm has competitive ratio 2.Jiang et.al [4] also considered online over list problem on two parallel machines with a single sever,and in the problem,a job has to be loaded by the sever before being processed and unloaded immediately by the sever after its processing.They provided an online algorithm with a competitive ratio 5/3.Su [6] consider online over time scheduling on two parallel machines with a single server.For general case,the author provided a LPT algorithm with a competitive ratio 2,and the lower bound isIf all jobs have unit setup time,the algorithm has competitive ratio 3/2,while the lower bound is
This paper study the online scheduling problem with a single server onmparallel-batch machines to minimize the makespan.We suppose that the capacity of batch is unbounded.First,we consider the special case that,for every job,the setup time is no smaller than the processing time,we provide a best possible online algorithm with competitive ratioFor general case,we present an online algorithm with competitive ratio 3.
§2.Lower bound
We consider parallel-batch machines scheduling with a single server.There aremmachines denoted byM1,M2,···,Mm.We denote the problem as follows:
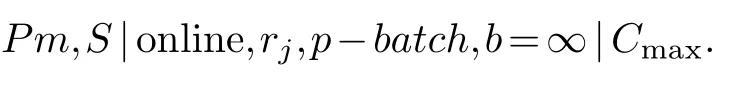
Denote the schedule given by online algorithm and by an optimal schedule byσandπ,respectively,whose objective values are denoted byConandCopt,respectively.Using adversary method,we will prove that the lower bound of competitive ratio of any online algorithm for the problem isLetαWe use the ordered pair (sj,pj) to denote that jobJjhas setup timesjand the processing timepj.Every job must start to process from the setup operation.
The first jobJ1with information(1,0)arrives at time 0.AssumeJ1is processed on machineM1.If the starting timet1≥α,then the completion time is at least 1+α,while the optimal schedule has objective value 1.SoCon/Copt≥1+α.
Ift1<α,once jobJ1begins to start,the second jobJ2with (1,0) arrives attime later,where0.No matterJ2is processed on any machine,it has to be started at or after timet1+s1.Hence,we haveCon≥t1+s1+s2+p2t1+2,while the optimal schedule will processJ1andJ2together as a single batch.i.e.,Coptt1++1.
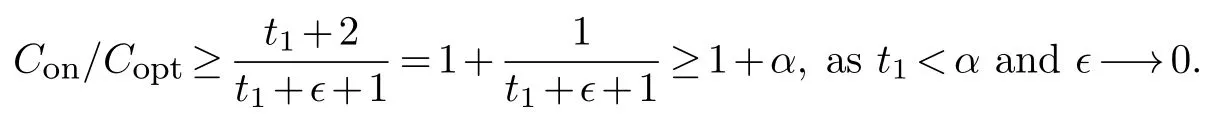
Therefore,we conclude below result.
Theorem 2.1.For the problem Pm,S|online,rj,p-batch,b∞|Cmax,any online algorithm has competitive ratio no less than
§3.Two online algorithms
Notations:
p(Bi) the processing time of batchBi,
s(Bi) the setup time of batchBi,
T(Bi) the starting time of batchBi,simple writtenTi,
C(Bi) the completion time of batchBi,simple writtenCi,
Ji1one of jobs with the processing time ofp(Bi),
Ji2one of jobs with the setup time ofs(Bi),
Bi(t) the running batch at timeton machineMi,
pi(t) the processing time ofBi(t),
si(t) the setup time ofBi(t),
Ti(t) the starting time ofBi(t),
p(t) the processing time of the waiting batch at timet,
s(t) the setup time of the waiting batch at timet.
If no batch is processed at timet,setBi(t)?andpi(t)si(t)Ti(t)0.Note that jobsJi1andJi2may be a common job.
AlgorithmAm:

Suppose that the online algorithmAmproducesnbatchesB1,B2,···Bnwith completion timesC1≥C2≥···≥Cn,respectively.Further suppose thatB1is scheduled on machineM1.ThenConC1T1+s(B1)+p(B1).Without loss of generality,we suppose that no batches start after time momentT1.
In the following discussion,we first consider a special case: supposesj ≥pj,i.e.,for every job,the setup time is no smaller than the processing time.If jobsJiandJjsatisfysi >sj,we can assume thatpi <pj,since if they have agreeable setup time and processing time,the one can overlap the other one.
In a feasible schedule for this problem,setup operations of distinct batches cannot be operated at the same time,even though they are processed on distinct machines.Hence,an optimal scheduleπhas the following properties.
Lemma 3.1.If jobs Ji and Jj are scheduled in different batches in π,then we have
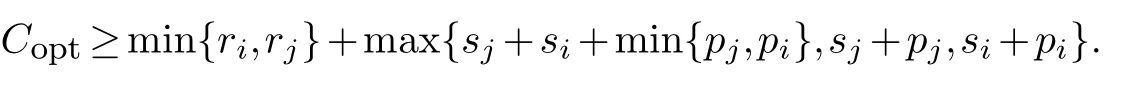
Lemma 3.2.If batch Bi exists in schedule σ,then the optimal schedule satisfies
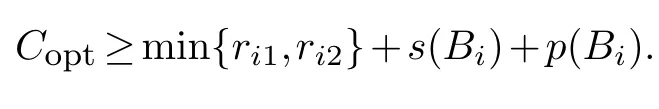
Proof.As above definitions,Ji1andJi2are one of jobs who has processing timep(Bi) and setup times(Bi),respectively,inBi,i.e.,pi1p(Bi) andsi2s(Bi).In optimal schedule,Ji1andJi2are scheduled either in a common batch or two different batches.By Lemma 3.1,we haveCopt≥min{ri1,ri2}+s(Bi)+p(Bi),orCopt≥min{ri1,ri2}+si1+si2+pi2.Note thatsi1≥pi1p(Bi).With the fact thatsi2s(Bi),we conclude thatCopt≥min{ri1,ri2}+s(Bi)+p(Bi).The result follows.
Lemma 3.3.If at time moment T1machine M1is idle,then Con/Copt ≤1+α.
Proof.If so,either some batches are processing on other machines or all other machines are idle at timeT1.The running batches (if exist) are denoted byBi(T1),fori2,3,···m,satisfyingT1≥Ti(T1)+si(T1),r11>Ti(T1) andr12>Ti(T1).LetBi(T1)?,Ti(T1)0 andsi(T1)0 ifBi(T1) does not exist for somei.Since machineM1is idle at time momentT1,by algorithmAm,we have
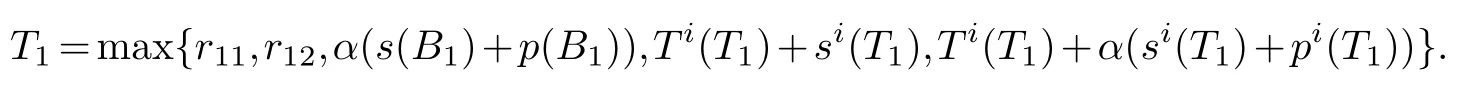
Case 1.T1r11orT1r12.It can be deducedr11r12.Otherwise,ifr11/r12,thenJ12would be processed beforeT1sinceT1≥max{α(s(B1)+p(B1)),Ti(T1)+α(si(T1)+pi(T1)),Ti(T1)+si(T1)},contradicting thatJ11andJ12are processed in a common batchB1.Therefore,we getConr11+s(B1)+p(B1) andCopt≥r11+max{s(B1),p(B1)}≥(1+α)max{s(B1),p(B1)}.Then we haveCon-Copt≤min{s(B1),p(B1)}≤αCopt.
Case 2.T1α(s(B1)+p(B1)).ThenConT1+s(B1)+p(B1)(1+α)(s(B1)+p(B1)).From Lemma 3.2,we haveCopt≥min{r11,r12}+S(B1)+P(B1).ThereforeCon/Copt≤1+α.


This completes the proof of Lemma 3.3.
Lemma 3.4.If time moment T1is equal to the completion time of some batch,then Con/Copt ≤1+α.
Proof.If there are more than one batch completing at timeT1,supposeB*is such a batch with the largest starting time on machineMi,thenT1T*+s(B*)+p(B*).While on other machines exceptMi,one of two following cases would happen: either some batch,sayBj,starts to process after time momentT*and completes after timeT1,i.e.,Tj ≥T*+s(B*) andT1≥Tj+s(Bj),or no such batch exists.
For the first case,we have max{r11,r12}>Tj ≥T*+s(B*).Further,using Lemma 3.2,we getCopt≥T*+s(B*)+s(B1)+p(B1).Then we conclude
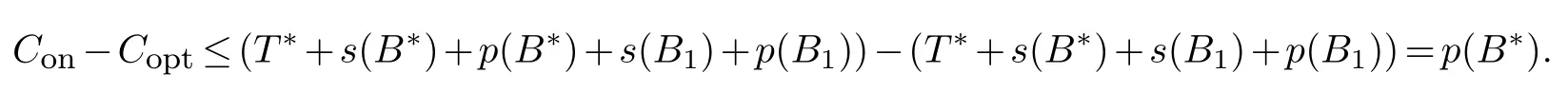
Sinces(B*)≥p(B*) and from Lemma 3.2,we haveCopt≥s(B*)+p(B*)≥2p(B*).Hence(Con-Copt)/Copt<α.
For the second case,if no such batch exists,we can argue that there must exist another batchBion other machines,contenting withTi <T*andCi ≥T1,i.e.,p(Bi)≥s(B*)+p(B*)ands(Bi)≥s(B*)+p(B*) sinces(Bi)≥p(Bi).Otherwise,by implementation of online algorithm,batchB1would be processed before the completion time ofB*rather than starting at timeC*.Using Lemma 3.2,we haveCopt≥s(Bi)+p(Bi)≥2(s(B*)+p(B*))andCopt≥T*+s(B1)+p(B1).Then we conclude
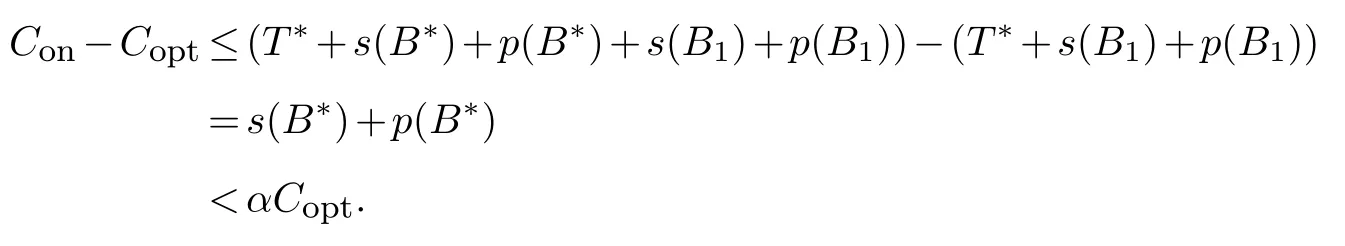
The result follows.
Theorem 3.1.For the problem Pm,S|online,rj,sj ≥pj,p-batch,b∞|Cmax,algorithm Am has competitive ratio
For the general case,the algorithmAmcannot produce a best possible schedule.For example,at time 0,two jobsJ1with information (1,0) andJ2with information (0,1) arrive.According to the algorithmAm,two jobs would be scheduled in a common batch and start at time moment 2α,thenCon2α+2≈3.236.And the optimal schedule would scheduleJ2first on a machine,and then scheduleJ1on another machine,soCopt1.ThusCon/Copt≈3.236.
In the following,we will provide the other algorithmHmwith competitive ratio 3 for the general case.
AlgorithmHm:

Theorem 3.2.For the online scheduling problem on parallel machines with a single server to minimize makespan,the competitive ratio of algorithm Hm is no greater than 3.
Proof.We use the same notations as above discussion and also suppose thatConT1+s(B1)+p(B1).There are three cases needed to consider.
Case 1.T1r11orT1r12.Then we haveCon-Copt≤max{s(B1),p(B1)}≤Copt.ThusCon/Copt≤2.
Case 2.T1T*+s(B*) where batchB*is the processing batch with the largest starting time at timeT1.Then we haveConT*+s(B*)+s(B1)+p(B1).Note that jobsJ11andJ12arrive after time momentT*.Therefore,Copt≥T*+p(B1),andCopt≥s(B*)+s(B1) (since setup operations cannot overlap).ThusCon-Copt≤s(B*)+s(B1)≤Copt,i.e.,Con/Copt≤2.
Case 3.T1Tk+s(Bk)+p(Bk) where batchBkis the completed batch with the largest starting time (if more than one) at timeT1.Then we haveConTk+s(Bk)+p(Bk)+s(B1)+p(B1).By the fact that two jobsJ11andJ12arrive after timeTk,two other jobsJk1andJk2arrive beforeTk,we haveCopt≥Tk+p(B1).ThenCon-Copt≤s(Bk)+p(Bk)+s(B1) .
In the optimal scheduleπ,if jobJk2is processed in different batches with one of jobsJk1orJ12,we haveCopt≥s(Bk)+min{p(Bk),s(B1)}.Thus
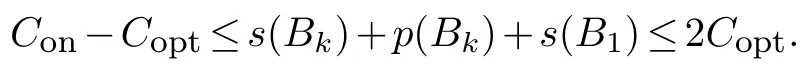
Otherwise,we supposeJk2is processed in a common batch with jobsJk1orJ12.ThenCopt≥Tk+s(Bk)+p(Bk).Therefore,we have
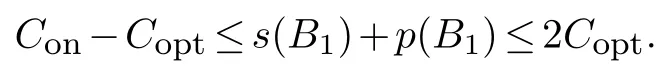
Both conclusions equalCon/Copt≤3.The result follows.
We have a tight example for algorithmHm.Suppose two jobsJ1with information (1,0) andJ2with information (0,1) arrive at time 0.According to the algorithmHm,we would process two jobs as a batch and start to setup immediately.Another two jobsJ3with information (1,0)andJ4with information (0,1) arrive at time.Then we haveCon1+1+13.While we have an optimal schedule that processesJ2andJ4as a batch first on one machine and then processJ1andJ3as the other batch on another machine.Therefore,Copt+1.Thus we haveCon/Copt3/(+1)-→3,as0.
§4.Conclusions
In this paper,we first proved that the scheduling problem on parallel-batch machines with a sever to minimize makespan has a lower boundFor special case thatsj ≥pj,we presented a best possible online algorithmAmwith competitive ratioFor general case,we provided a tight algorithmHmwith a competitive ratio 3.There leaves a gap betweenand 3.Our future work is to design a best possible online algorithm for general case.According to the above tight example,we can find that sometimes we have to depart waiting jobs into different batches to process,which is very important to design a better algorithm.
 Chinese Quarterly Journal of Mathematics2022年4期
Chinese Quarterly Journal of Mathematics2022年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- Profile of Mr.Yixun Lin
- A Note on the Girth of 3-Regular Hamiltonian Graph
- Characterizations of Cycle-Forced 2-Connected Claw-Free Cubic Graphs
- Research on Unbounded Parallel-Batch Scheduling with Jobs Having Set-Up Times
- A Note on Single-Machine Lot Scheduling with Splittable Jobs to Minimize the Number of Tardy Jobs
- A Note on Two-Agent Scheduling with Rejection on a Single Machine
