(1.College of Information and Management Science,Henan Agricultural University,Zhengzhou 450003,China;2.School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China)

Abstract: In a recent paper,Feng et al.[5] (Two-agent scheduling with rejection on a single machine.Appl.Math.Model.39 (2015) 1183-1193) studied some two-agent scheduling problems with rejection on a single machine.The authors showed that all problems are NP-hard and then provided four dynamic programming algorithms.Unfortunately,we observe that some mistakes are contained in the two dynamic programming algorithms.In this note,we first show by a counter-example that the above two algorithms are incorrect.Furthermore,we also provide two new dynamic programming algorithms to solve the same problems.

Keywords: Two-agent scheduling;Single machine;Rejection;Dynamic programming

§1.Introduction

Multi-agent scheduling was first introduced by Baker and Smith [3] and Agnetis et al.[2].In a multi-agent scheduling problem,there are several agents and each agent is associated to a subset of jobs.Each agent has its own objective function which depends on the completion times of its jobs only.However,all the jobs have to share common resources.The objective is to find a schedule of the jobs of all agents,which constitutes a good compromise solution.Today,multi-agent scheduling (especially two-agent scheduling) has developed into a hot topic in scheduling research.According to the current data from web of science,there are 3660 articles which studied “multi-agent scheduling”.For a more detailed models and results on multi-agent scheduling,we refer the reader to the survey paper by Perez-Gonzalez and Framinan [8] and the book by Agnetis et al.[1].

Scheduling with rejection was first studied by Bartal et al.[4].In a scheduling problem with rejection,each job is either accepted and then processed on some machine,or rejected by paying a certain rejection penalty.In recent years,there has been significant interest in scheduling with rejection.According to the current data from web of science,there are 2359 articles which considered “scheduling with rejection”.For a more detailed survey on this topic,the interested reader is referred to the survey paper by Shabtay et al.[9].

Although a larger number of results have been obtained in multi-agent scheduling or scheduling with rejection,it seems that only a few of papers considered the combination of two scheduling models,i.e.,multi-agent scheduling with rejection.To the best of our knowledge,the earliest paper on two-agent scheduling with rejection is the one by Feng et al.[5].They studied the two-agent scheduling problem with rejection on a single machine.The authors showed that all problems are NP-hard and then provided four dynamic programming algorithms.Furthermore,they presented a 2-approximation algorithm and a fully polynomial-time approximation scheme(FPTAS).Mor and Mosheiov [7] considered a two-agent scheduling problem with rejection and precedence constraints on a single machine.The objective is to find a schedule such that the maximum cost is minimized.They provided a polynomial-time algorithm for this problem.Li and Lu [6] further studied the two-agent scheduling problem with rejection on parallel machines.The authors considered four scheduling problems associated with different combinations of the two agents’ objective functions.Some pseudo-polynomial time algorithms and a fully polynomial-time approximation scheme are presented for the above problems.

The rest of this paper is organized as follows.In Section 2,we present the problem formulation for two-agent scheduling with rejection.In Section 3,we provide a counter-example to show that two dynamic programming algorithms in[5]are incorrect.Finally,two new dynamic programming algorithms are presented in Section 4.

§2.Problem formulation

§3.Counter-example

3.1.Problem 1|reject|+e(RA):+e(RB)≤Q

Combining the above four cases,Feng et al.[5]presented the following dynamic programming algorithm.

Algorithm DP1

The boundary conditions:

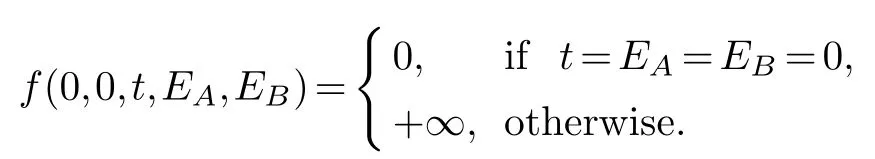
The recursive function:

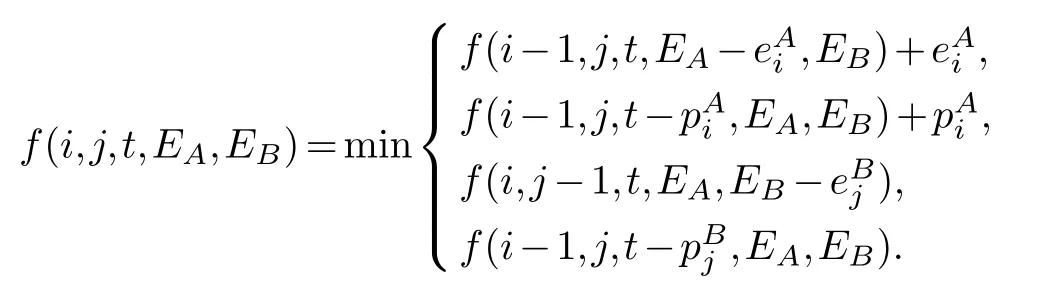
The optimal value is given by

Remark 3.2.We also observe that in Case 3 and Case 4,whenever is rejected or processed on the machine,the objective function value of agent B is increased.It is easy to see that the feasibility of B-jobs in Case 4 is checked to guarantee the current value of agent B is not greater than Q,but it is not checked in Case 3.Thus,Case 3 is incorrect since it is possible to be infeasible.

A small counter-example is constructed as follows:

Finally,we also havef(1,1,t,EA,EB)+∞(otherwise).

Thus,by algorithm DP1,the optimal value is given by

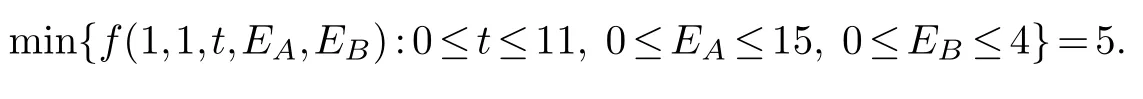
Meanwhile,we havef(1,1,11,0,0)5 (By Remark 3.1,the recursive function in Case 2 is incorrect) andf(1,1,5,0,4)5 (By Remark 3.2,it is infeasible sinceEB4＞3Q).Thus,the above counter-example implies that algorithm DP1 is incorrect.

3.2.Problem 1|reject|∑+e(RA):+e(RB)≤Q

§4.New dynamic programming algorithms

From Remark 3.2 and Remark 3.3,the main errors of algorithms DP1 and DP3 are in Case 3.Thus,in order to check the feasibility in Case 3,we have to add a status variableLBwhich is the currentvalue.Furthermore,we assume thatQ≤min{E2,P}.Otherwise,ifQ≥min{E2,P},then allB-jobs can be rejected or processed after allA-jobs.Thus,the two-agent problems are equivalent to the corresponding single-agent problems.Now,we have the following dynamic programming algorithms.

4.1.Problem 1|reject|+e(RA):+e(RB)≤Q

Combining the above four cases,we provide the following dynamic programming algorithm DP2.

Algorithm DP2

The boundary conditions:

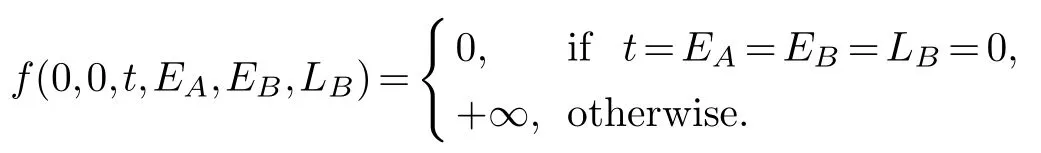
The recursive function:

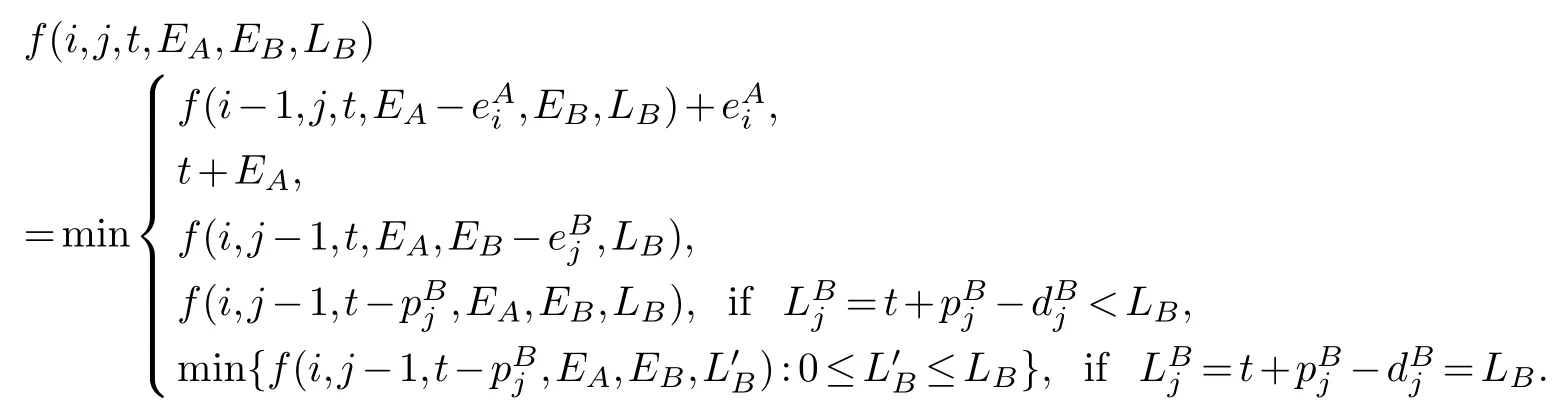
The optimal value is given by

4.2.Problem 1|reject|∑+e(RA):+e(RB)≤Q

Combining the above four cases,we provide the following dynamic programming algorithm DP3.

Algorithm DP3

The boundary conditions:

The recursive function:

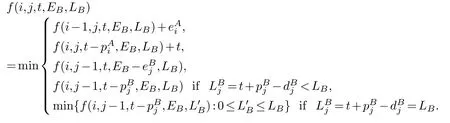
The optimal value is given by