A NONLINEAR SCHR?DINGER EQUATION WITH COULOMB POTENTIAL?
Changxing MIAO()
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
E-mail:miao changxing@iapcm.ac.cn
Junyong ZHANG()
Department of Mathematics,Beijing Institute of Technology,Beijing 100081,China;Department of Mathematics,CardiffUniversity,UK
E-mail:zhang junyong@bit.edu.cn;ZhangJ107@cardiff.ac.uk
Jiqiang ZHENG()
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
E-mail:zhengjiqiang@gmail.com
Abstract In this paper,we study the Cauchy problem for the nonlinear Schr?dinger equations with Coulomb potential i?t u+?u+=λ|u|p?1u with 1
Key words nonlinear Schr?dinger equations;long range potential;global well-posedness;blow-up;scattering
Dedicated to Professor Banghe LI on the occasion of his 80th birthday
1 Introduction
We study the initial-value problem for the nonlinear Schr?dinger equations with Coulomb potential of the form
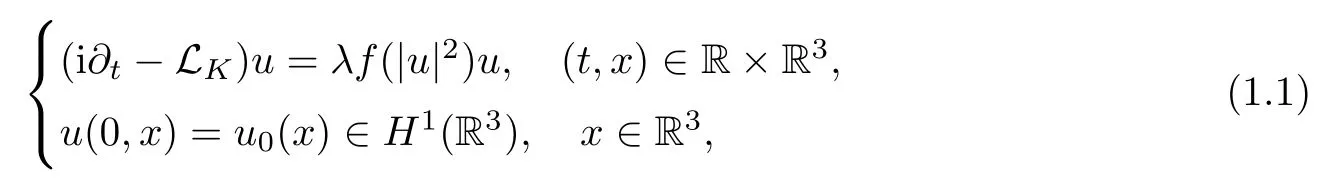

The study of the operator LK=???K|x|?1with the Coulomb potential is of both physical and mathematical interest.This operator withK>0 provides a quantum mechanical description of the Coulomb force between two charged particles and corresponds to having an external attractive long-range potential,due to the presence of a positively charged atomic nucleus.One can refer to [32,38]for more on these models of the hydrogen atom in quantum physics fields.
The mathematical interest and challenge in these equations however comes from the operator theory with a long range decay potential and the dispersive behavior of the solution.Due to the long range effect of the Coulomb potential,it is known that the strong limit
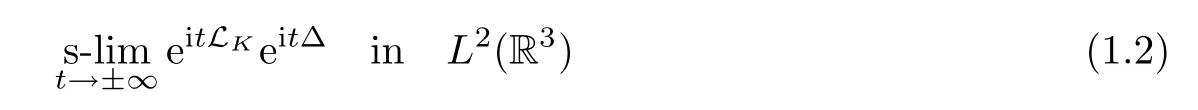
doesnot exist,and neither doeswaveoperator;see Reed-Simon [36].Therefore,for the Coulomb potential case,there is no possibility to study the classical scattering theory;one cannot expect that the solutionuto(1.1)satisfies that
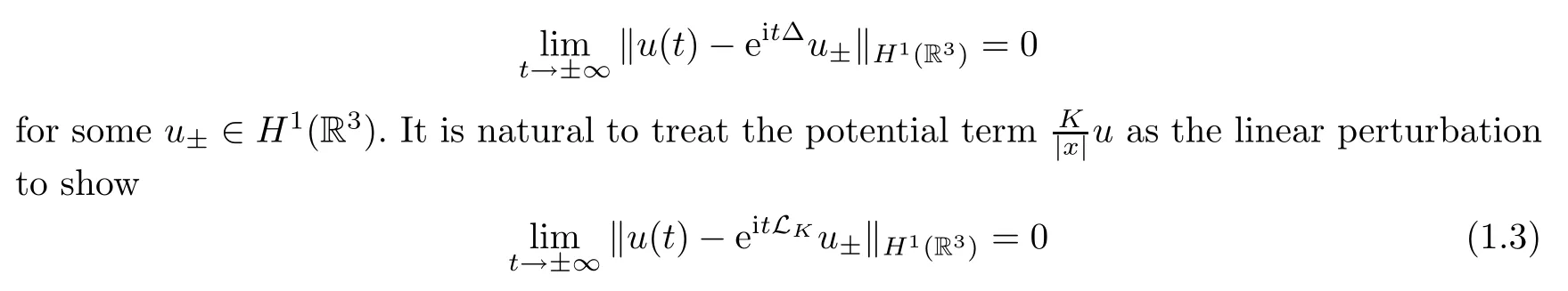
for someu±∈H1(R3).However,the equation(1.1)have been studied extensively.In particular,the existence of a unique strong global-in-time solution to(1.1)with Hartree nonlinearityf(|u|2)=|x|?1?|u|2goes back to [6].For whenK≤0,the solutionu(t)to(1.1)with the Hartree nonlinearity was studied in [10,18],where the authors proved the global existence and a decay rate for the solution,however,they needed the initial data in a weighted-L2space.For whenK>0,Lenzmann and Lewin [29]proved that a time average estimate holds for everyR>0 such that
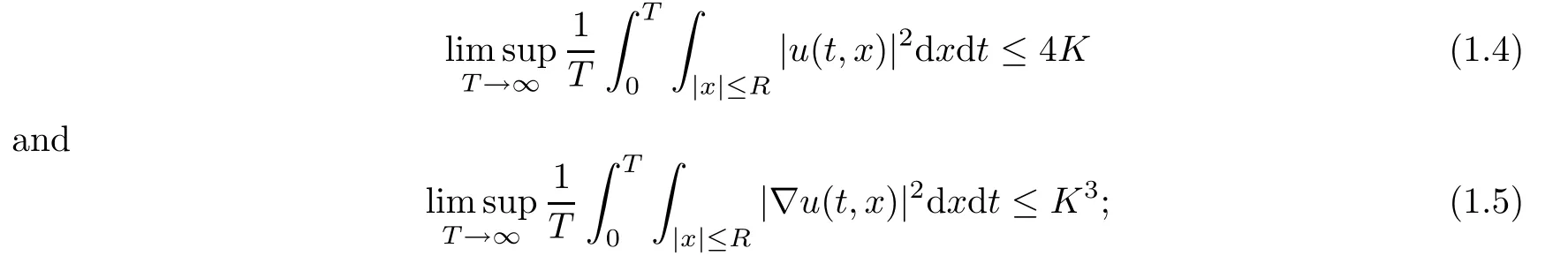
this is related to the RAGE theorem(see Reed-Simon [36]).
In this paper,we will study the Cauchy problem for the nonlinear Schr?dinger equation(1.1)with initial data in the energy spaceH1(R3).The Cauchy problem(including the global existence and scattering theory)for the nonlinear Schr?dinger equation without potential,i.e.,K=0,was intensively studied in [5,16].Due to the perturbation of the long range potential,many basic tools which were used to study the nonlinear Schr?dinger equation were different,and even failed.For instance,the global-in-time Strichartz estimate fails whenK>0;see(2.5)below.This is a big issue for proving the scattering theory(such as(1.3)),but we show the global existence.In the caseK<0,Mizutani [33]recently obtained the global-in-time Strichartz estimate.This possibly leads to the nonlinear scattering result(1.3).However,we have to overcome some difficulties in order to establish analysis tools associated with the operator LK.To our purposes,we first establish the Sobolev space theory associated with the self-adjoint operator LK.In this repulsive case,we will establish an interaction Morawetz estimate for the defocusing case,which provides us with a decay of the solutionuto(1.1).
Before stating our main results,we introduce some background material.
Equation(1.1)admits a number of symmetries inH1(R3),explicitly
?Phase invariance:ifu(t,x)solves(1.1),then so does ei γu(t,x), γ∈R;
?Time translation invariance:ifu(t,x)solves(1.1),then so doesu(t+t0,x),t0∈R.
From the Ehrenfest law or direct computation,these symmetries induce invariances in the energy space,namely,mass
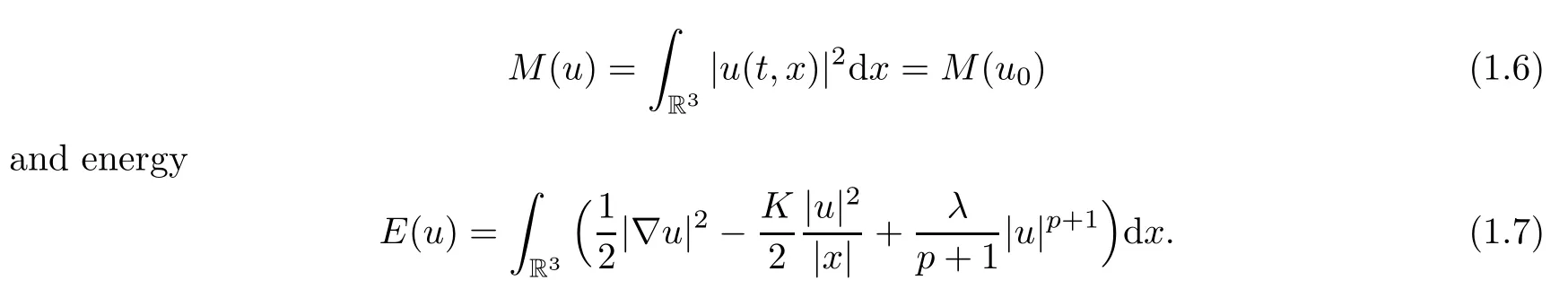
Compared with the classical Schr?dinger equation(i.e.,(1.1)withK=0),equation(1.1)is not space translation invariant,which induces the situation whereby the momentum
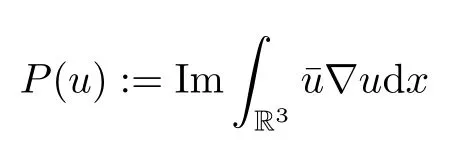
is not conserved.
One of the motivations for considering this problem is the failure of the equation to be scale invariant.Removing the potential termone recovers the classical nonlinear Schr?dinger equation
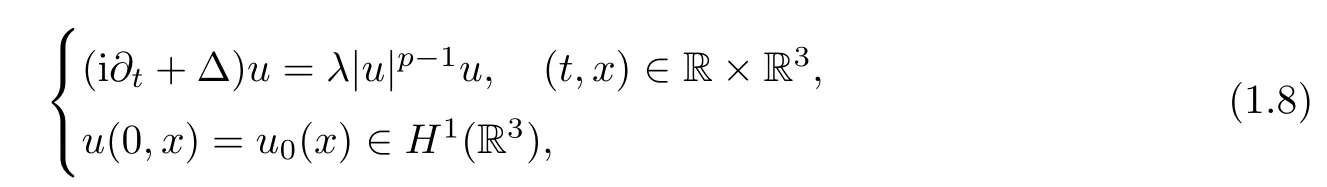
which is scaling invariant.That is,the class of solutions to(1.8)is left invariant by the scaling
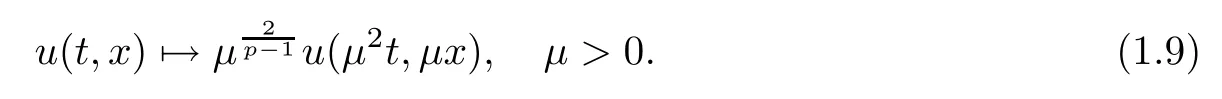
Moreover,one can also check that the only homogeneousSobolev space that is left invariant under(1.9)isWhensc<1,the problem is called the energy-subcritical problem.The problem is known as energy-critical problem whensc=1.There are a number of works studying the problems:we refer the reader to [4,5,8,17,37,43]for defocusing case in the energy-subcritical and energy-critical cases,and to [11–14,19,23,26]for the focusing case.It is known that the defocusing case is different from the focusing one due to the opposite sign between the kinetic energy and potential energy.
The purpose of this paper is to understand the influence of the long range potential on the existence theory and the scattering theory for the nonlinear Schr?dinger equation.For example,the solution has global existence no matter what the sign of K,but it scatters whenK<0 anddoes not scatter whenK>0,even in the defocusing case.
As mentioned above,the focusing caseisdifferent from the defocusing case.In the focusing case(λ=?1),we will also use the energy without potential
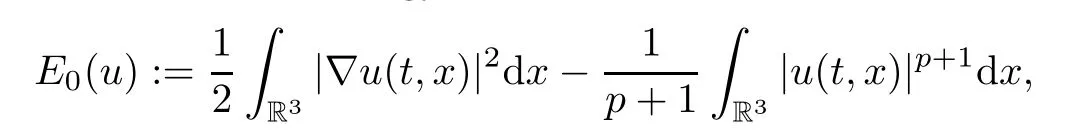
to givethethreshold for a global/blowup dichotomy.Aswith theargument used in our previous works [24,25,31]considering NLSwith an inverse square potential,in the caseK<0,we will consider the initial data below the threshold of the ground stateQto the classical elliptic equation
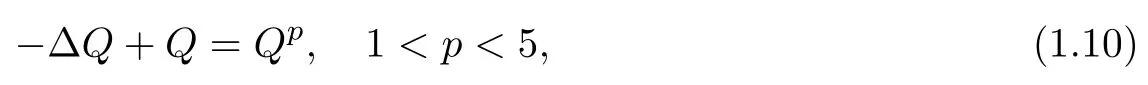
due to the sharp constant in the Gagliardo-Nirenberg inequality
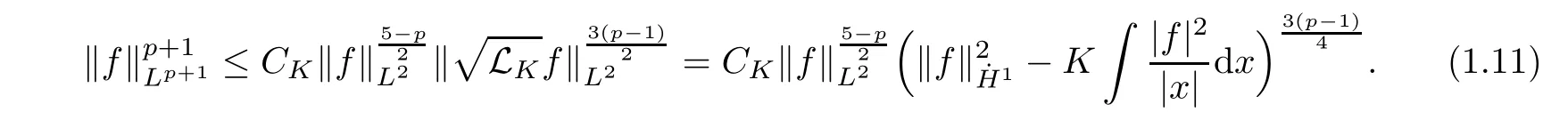
LetC0be the sharp constant of the classical Gagliardo-Nirenberg inequality
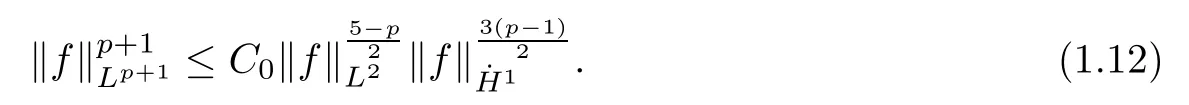
Then we claim thatCK=C0,and it is well-known that the equality in(1.12)withK=0 is attained byQ,but we will see that equality in(1.11)withK<0 is never attained.Indeed,by the sharp Gagliardo-Nirenberg inequality for(1.12),we find that

Thus,C0≤CK.However,for anyf∈H1{0}andK<0,the standard Gagliardo-Nirenberg inequality implies that
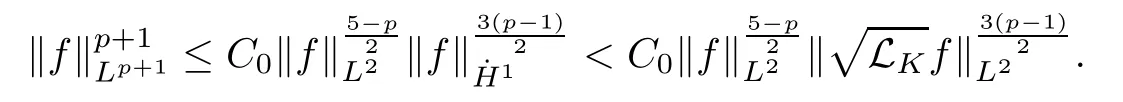
ThusCK=C0,and the last estimate also shows that the equality is never attained.
In the energy-critical case(sc=1),we consider the ground stateWto be the elliptic equation
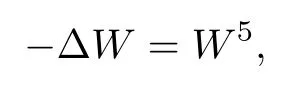
due to the sharp constant in the Sobolev embedding.We refer to [1,15,28]for more regarding the existence and uniqueness of the ground state.
Now,we state our main results.First,we consider the global well-posedness theory for problem(1.1).
Theorem 1.1(Global well-posedness)LetK∈R andu0∈H1(R3).Suppose that 0 ?ifp?1=(mass-critical),assume thatM(u0) ?ifp?1=4(energy-critical)andK<0,assume thatu0is radial2Here the restriction K<0 induces us to utilize the result of Kenig-Merle [23]in which one needs a radial initial data.and Then,there exists a unique global solutionu(t,x)to(1.1)such that for anyI?R compact and(q,r)∈ Λ0that is admissible as defined below. Remark 1.2The picture of the global existence is almost completed in the defocusing case regardless of whether it is so in the repulsive or attractive case.The focusing case is more complicated and the blow up result below is a supplement of this global existence. Next,we study the long-time behavior of the above global solution,such as the scattering theory.We say that a global solutionuto(1.1)scatters if there existsu±∈such that It is known that the global-in time Strichartzm estimate plays an important role in the scattering theory.In fact,with the global-in time Strichartz estimate in hand,the standard arguments show that the scattering result of the global solution is a consequence of the global Strichartz-norm boundednessHowever,in the attractive case,i.e.,K>0,the global-in-time Strichartz estimate does not hold(see Subsection 2.2 below).Thus,we do not know whether the solutionuto(1.1)withK>0 scatters or not,even for the small initial data.For the repulsive case,i.e.,K<0,using the global-in-time Strichartz estimates [33]and the Sobolev norm equivalence(1.18)below,one can easily obtain the scattering result for the small initial data.For the general initial data,we will get the scattering result in the defocusing energy-subcritical case(λ=1,p<5)by establishing the interaction Morawetz estimate,which gives a global Strichartz-norm boundedness. In the caseK>0,we know from [3,Lemma 6]that there is a positive solutionf(x)∈H2of the elliptic equation This implies that there is a solitonu(t,x):=eitf(x)that solves(1.1)withλ=1.We remark that such a soliton is global but does not scatter.In physics,the equation(1.16)arises in the Thomas-Fermi-von Weizsacker(TFW)theory of atoms and molecules [2,30]without electronic repulsion.There,K|x|?1is the electric potential due to a fixed nucleus of atomic numberKlocated at the origin,f(x)2stands for the electronic density,and Rf(x)2dxis the total number of electrons. In contrast,for the caseK≤0,we will derive the quadratic Morawetz indentity for(1.1)and then establish the following interaction Morawetz estimate forλ=1 This provides us a decay of the solutionuto(1.1).Combining this with Strichartz estimate and Leibniz rule obtained by the Sobolev norm equivalence we establish the scattering theory as follows: Theorem 1.3(Scattering theory)LetK≤0, In the focusing case,i.e.,λ=?1,by the classical Virial argument,one can obtain the blow-up result for the negative energy. Theorem 1.4(Blow-up result)LetK∈R, (i)Letu0∈Σ:={u0∈H1,xu0∈L2}.Then,the solutionuto(1.1)blows up in both time directions,in one of the following three cases: (1)C(E(u0),M(u0))<0; (2)C(E(u0),M(u0))=0,y′(0)<0; (ii)Letu0∈H1(R3)be radial,and assume thatC(E(u0),M(u0))<0.Then,the solutionuto(1.1)blows up in both time directions. The paper is organized as follows:in Section 2,we give somenotations,recall the Strichartz estimate,and prove the Sobolev space equivalence.Section 3 is devoted to proving global wellposedness,i.e.,Theorem 1.1.We show the interaction Morawetz-type estimates in Section 4,and we utilize these Morawetz-type estimates and the equivalence of the Sobolev norm to prove Theorem 1.3.Finally,we use the Virial argument to obtain the blow-up result(Theorem 1.4)in Section 5. In this section,we first introduce some notations,and then recall the Strichartz estimates.We conclude this section by showing the Sobolev space equivalence between the operator LKand Laplacian operator??. First,we give some notations which will be used throughout this paper.To simplify the expression of our inequalities,we introduce some symbols?,~,?.IfX,Yare nonnegative quantities,we useX?YorX=O(Y)to denote the estimateX≤CYfor someC,andX~Yto denote the estimateX?Y?X.We denotea±to be any quantity of the forma±?for any?>0. giving rise to the fractional differentiation operators|?|sand〈?〉s,defined by where〈ξ〉:=1+|ξ|.This helps us to define the homogeneous and inhomogeneous Sobolev norms Next,we recall the well-known Lorentz space and some properties of this space that are relevant for our purposes.Given a measurable functionf:R3→C,define the distribution function offas and its rearrangement function as For 1≤p<∞and 1≤r≤∞,define the Lorentz quasi-norm We refer to O’Neil [34]for the following H?lder inequality in Lorentz space: Proposition 2.1(H?lder’s inequality in Lorentz space)Letting 1≤p,p0,p1<∞and 1≤r,r0,r1≤∞, It is well known that the Strichartz estimate is very useful in the study of nonlinear dispersive equations.To state the result,we define Theorem 2.2(Local-in-time Strichartz estimate)LetK∈R and LKbe as above.For(q,r)∈ Λ0,it holds that We regard the Coulomb potential as an inhomogeneous term,hence we have,by Duhamel’s formula,that For our purposes,we recall the inhomogeneous Strichartz estimate without potential on the Lorentz space. Lemma 2.3(Strichartz estimate for eit?,[22,35])For(q,r),(q1,r1)∈ Λ0,we have that Using the above lemma,we show that We use the above inhomogeneous Strichartz estimate to obtain that where we use the mass conservation in the last inequality.Therefore,we have proven(2.3). □ It is natural to ask whether or not the global-in-time Strichartz estimate holds.The answer is that the global-in-time Strichartz estimate does not hold in the attractive caseK>0,but holds in the repulsive caseK≤0. To see the attractive case,a simple computation shows that LettingcK=K/2,this implies that For the repulsive Coulomb potential case,Mizutani [33]recently proved the global-in-time Strichartz estimate,where the proof employs several techniques from linear scattering theory such as the long time parametrix construction of Isozaki-Kitada type [21],propagation estimates,and local decay estimates. Theorem 2.4(Global-in-time Strichartz estimate,[33])For(q,r),(q1,r1)∈ Λ0andK<0,it holds that As mentioned in the introduction,we need a fractional chain rule in the proof of scattering theory whenK<0.TheLp-product rule for fractional derivatives in Euclidean spaces which will be proven in the next subsection. In this subsection,we study the relationship between Sobolev spaceadapted with Laplacian operator perturbed by Coulomb potential and a classical Laplacian operator;that is,for suitablesandpsuch that where〈a〉=(1+|a|2)1/2.To this end,we recall the following heat kernel estimate: Lemma 2.6(Heat kernel)LetK<0 and let LKbeas above.Then there exist constantsC,c>0 such that Lemma 2.7(Sobolev norm equivalence)LetK<0,1 ProofThe proof is classical and follows from heat kernel estimate and Stein complex interpolation.We refer to Y.Hong [20]or the authors of [44],but we give a complete proof for convenience. First,we considers=2.Using the Hardy inequality [44,Lemma 2.6]withp<3,we obtain that This implies(2.10)withs=2. holds for 1 In this section,we prove the well-posedness for Equation(1.1),including local and global well-posedness.In this part,we only use the classical Strichartz estimate for the Schr?dinger equation without potential i?tu??u=0 on the Lorentz space. In the energy-subcritical case(i.e.,p?1<4),the global well-posedness will follow from the local well-posedness theory and uniform kinetic energy control In the energy-critical case(p?1=4),we prove the global well-posedness by using a perturbation argument and the well-known scattering theory for Schr?dinger without potential in [8,23]. Theorem 3.1(Local well-posedness,energy-subcritical)LetK∈R,0 by takingTsmall such that On the other hand,foru,v∈B(I),we get,by the Strichartz estimate,that by takingTsmall such that A standard fixed point argument gives a unique local solutionu:[0,T]×R3→C to(1.1). □ By the local well-posedness theory and mass conservation,the global well-posedness will follow from the uniform kinetic energy control We argue the following several cases: Case 1:the defocusing case,i.e.,λ=1.In the defocusing case,we have the uniform bound In fact,we have,by Hardy’s inequality and Young’s ineqaulity,that which implies that and hence, Therefore we can extend the local existence to be a global one. This,together with(3.6),implies that Thus we can obtain the global existence by extending the local solution. From(3.6),we obtain that One the other hand,we have,by the sharp Gagliardo-Nirenberg inequality,that Hence, This shows that Then,there existsδ>0 such that By the sharp Gagliardo-Nirenberg inequality,we have that with the sharp constant This shows,forK<0,that for anyt∈I.This,together with implies that Using a continuity argument,together with the observation that we obtain that In sum,we obtain the uniform kinetic energy control in the maximal life-span.This concludes the proof of Theorem 1.1. SinceK<0,it is easy to get(3.11)from(3.12). Now,we assume(3.11).By the sharp Gaglilardo-Nirenberg’s inequality, This,together with the assumptionM(u0)E(u0)≤(1?δ)M(Q)E0(Q)and(3.13)yields that (ii)By the same argument as in(i),forK<0,λ=?1 andp=5,under the assumptionE(u0) is equivalent to We will show the global well-posedness by controlling global kinetic energy and proving“good local well-posedness”as in Zhang [45].More precisely,we will show that there exists a small constantT=such that(1.1)is well-posed on [0,T],which is referred to as being“good local well-posed”.On the other hand,since the equation in (1.1) is time translation invariant,this“good local well-posed”combined with the global kinetic energy control gives,immediately,the global well-posedness. Step 1:Global kinetic energy.For the defocusing case(λ=1),it follows from Case 1 in Subsection 3.2 that Meanwhile,for the focusing case(λ=?1)andK<0,under the restriction we easily obtain that Hence,we have,by coercivity as in [23],that Thus,we have derived the global kinetic energy. Step 2:Good local well-posedness.To obtain this,we first introduce several spaces and give estimates of the nonlinearities in terms of these spaces.For a time slabI?R,we define Then,we have,by H?lder’s inequality and the Sobolev embedding,that Now,it follows,from [8]for the defocusing case(λ=1)and [23]for the focusing case(λ=?1)under the assumption(3.18)andu0radial,that the Cauchy problem is globally well-posed and the global solutionvsatisfies the estimate for all(q,r)∈ Λ0.Thus,to recoveruon the time interval [0,T],whereTis a small constant to be specified later,it is sufficient to solve the difference equation ofωwith 0-data initial on the time interval [0,T], In order to solve(3.24),we subdivide [0,T]into finite subintervals such that,on each subinterval,the influence ofvto the problem(3.24)is very small. Letting?be a small constant,from(3.23),we can divide R into subintervalsI0,···,IJ?1such that,on eachIj, Thus,without loss of generality,and renaming the intervals if necessary,we can write withJ′≤J,and on eachIj Now we begin to solve the difference equation(3.24)on eachIjby inductive arguments.More precisely,we show that,for each 0≤j≤J′?1,there exists a unique solutionωto(3.24)onIjsuch that We mainly utilize an induction argument.Assuming that(3.24)has been solved onIj?1and that the solutionωsatisfies the bound(3.26)toj?1,it is enough to derive the bound of theωonIj. Defi ne the solution map and a set Thus we can choose?andTsmall,depending only on the Strichartz constant such that On the other hand,by an argument similar to that before,we have,forω1,ω2∈B,that which allows us to derive by taking?,Tsmall such that A standard fixed point argument gives a unique solutionωof(3.24)onIjwhich satisfies the bound(3.26).Finally,we get a unique solution of(3.24)on [0,T]such that Since on [0,T],u=v+ω,we obtain a unique solution to(1.1)on [0,T]such that As we mentioned before,this“good local well-posedness”combined with the“global kinetic energy control”seen in Step 1,finally gives the global well-posedness.However,since the solution is connected one interval by another,it does not have a global space-time bound.In what follows,we will discuss the defocusing case,in which the global solution has enough decay to imply scattering. In this section,we establish an interaction Morawetz estimate and the scattering theory in Theorem 1.3.Throughout the whole of the section,we work with the defocusing case with repulsive potential;that is,K<0 andλ=1. In this subsection,we establish the interaction Morawetz estimate for(1.1)withK<0 andλ=1. Lemma 4.1Letu:R×R3→C solve i?tu+?u+V(x)u=N,and N∈R.Given a smooth weightw:R3→R and a(sufficiently smooth and decaying)solutionuto(1.1),we define Then,we have that ProofFirst,noting that we get that Furthermore, ProofWe consider the NLS equation in the form of whereg=g(ρ,|x|)is a real function ofρ=|u|2=2T00and|x|.We first recall the conservation laws for the free Schr?dinger in Tao [41], for allj,k=1,···,n,andδjkis the Kroncker delta.Noting that the kinetic terms are unchanged,we see,that for(4.7), By the density argument,we may assume sufficient smoothness and the decay at infinity of the solutions and,in particular,the integrations by parts.Lethbe a sufficiently regular real even function defined as in R3,e.g.h=|x|.The starting point is the auxiliary quantity Now we use the global-in-time interaction Morawetz estimate(4.6) to prove the scattering theory part of Theorem 1.3.Since the construction of the wave operator is standard,we only show the asymptotic completeness. Letube a global solution to(1.1).Letη >0 be a small constant,to be chosen later,and split R intoL=L(‖u0‖H1)finite subintervalsIj=[tj,tj+1]such that Plugging this into(4.18)and noting thatα θ(p?1)>0,we can chooseηto be small enough such that Hence,we have,by the finiteness ofL,that Case 2:p∈(4,5),we use interpolation to show that whereα>0,β, γ≥0 satisfyα+β+γ=1 and Hence,arguing as above,we obtain(4.19). Finally,we utilize(4.19)to show asymptotic completeness.We need to prove that there exist uniqueu±such that Asttends to+∞,the limitation of(4.20)is well defined.In particular,we find the asymptotic state Therefore,we have concluded the proof of Theorem 1.3. In this section,we study the blow up behavior of the solution in the focusing case,i.e.,λ=?1.In the case in whichK>0,we will use the sharp Hardy’s inequality and Young’s inequality to obtain that which impliesIis finite,provided that (i)C(E,M)<0; (ii)C(E,M)=0,y′(0)<0; (iii)C(E,M)>0,y′(0)2≥24(p?1)C(E,M)y(0).In fact,with the above conditions,we haveT<+∞and which implies thatublows up in finite time by the same argument as in Case 1,since,for the caseK>0,the assumption shows that there exists 0<δ?1 such that AcknowledgementsWe are grateful to R.Killip,J.Murphy and M.Visan for useful discussions.
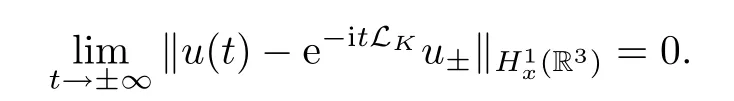

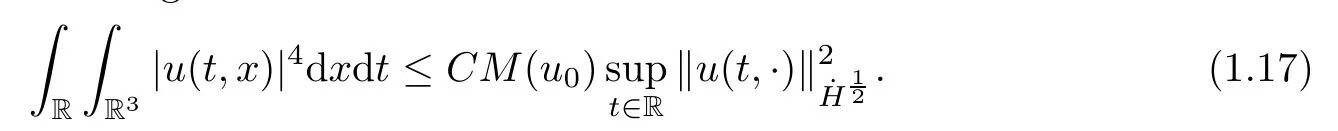


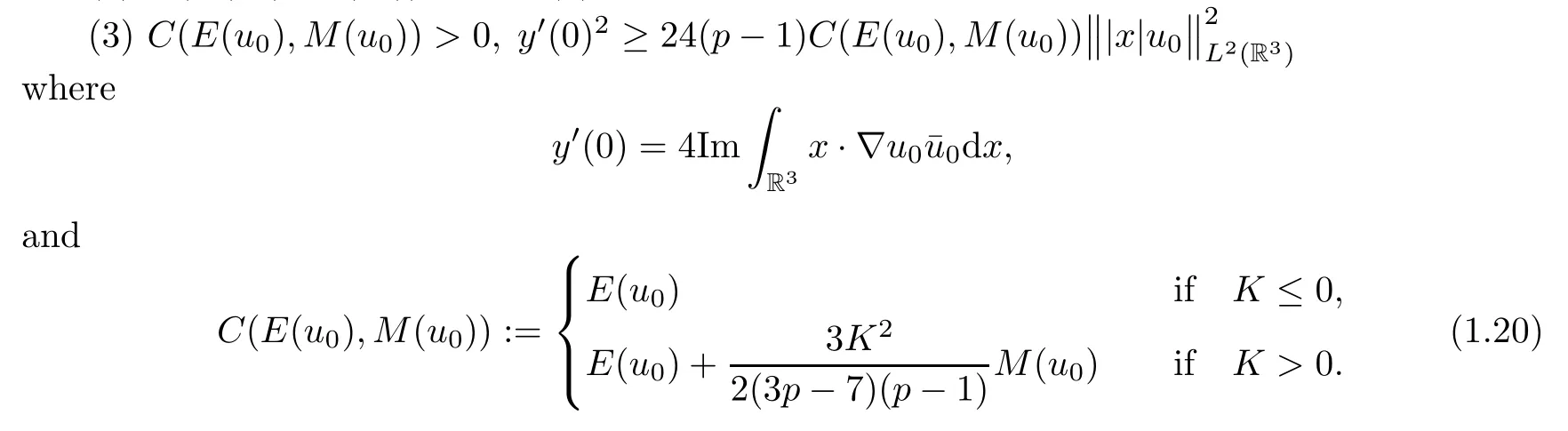
2 Preliminaries
2.1 Notations

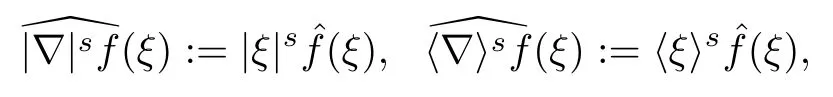
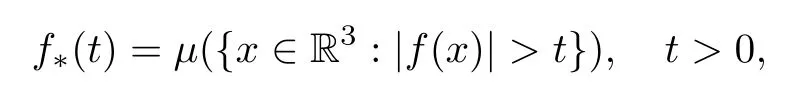
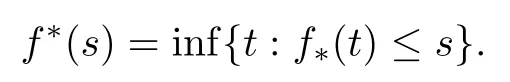
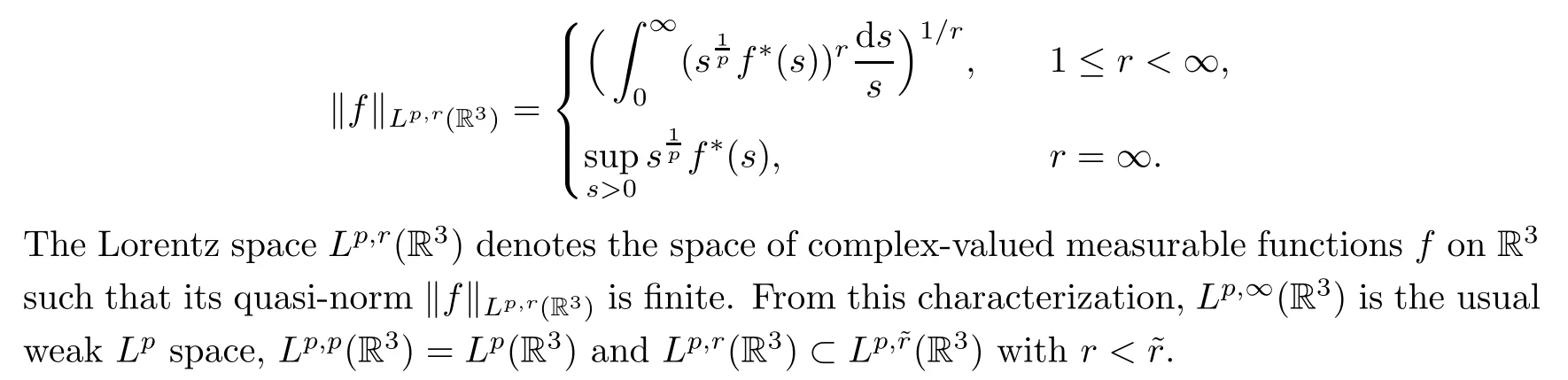
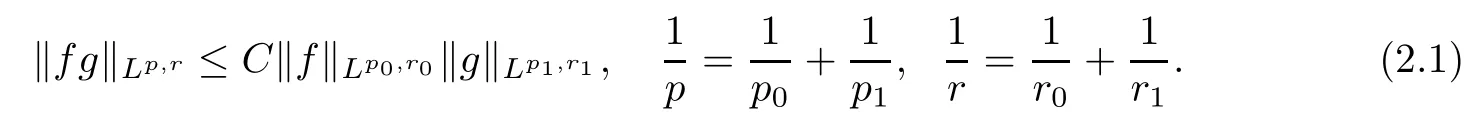
2.2 Strichartz Estimate

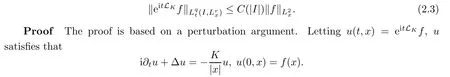
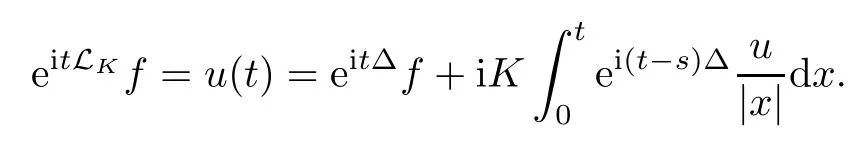
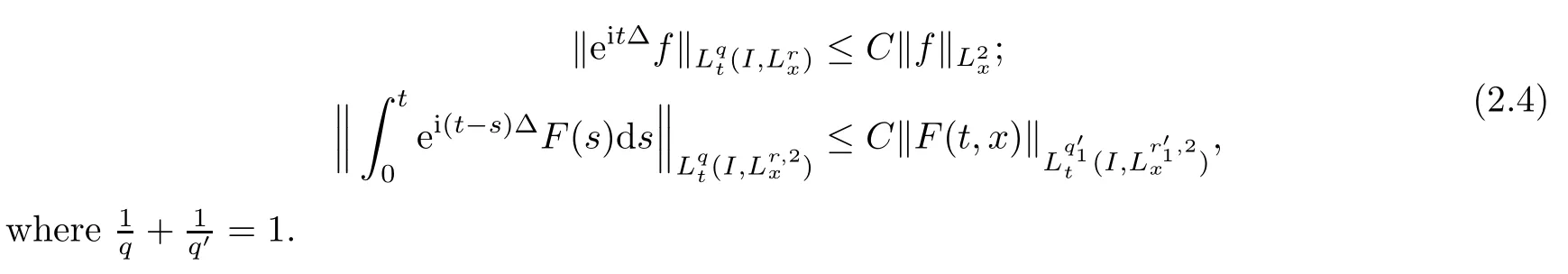


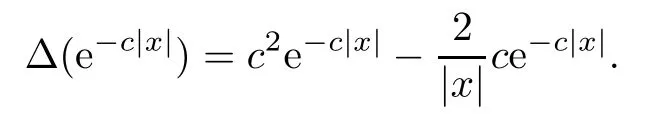
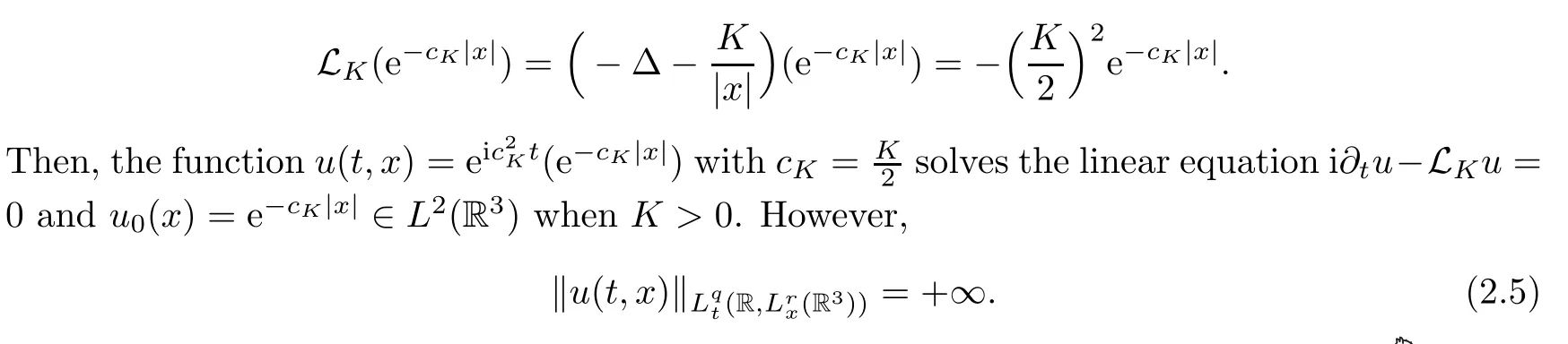
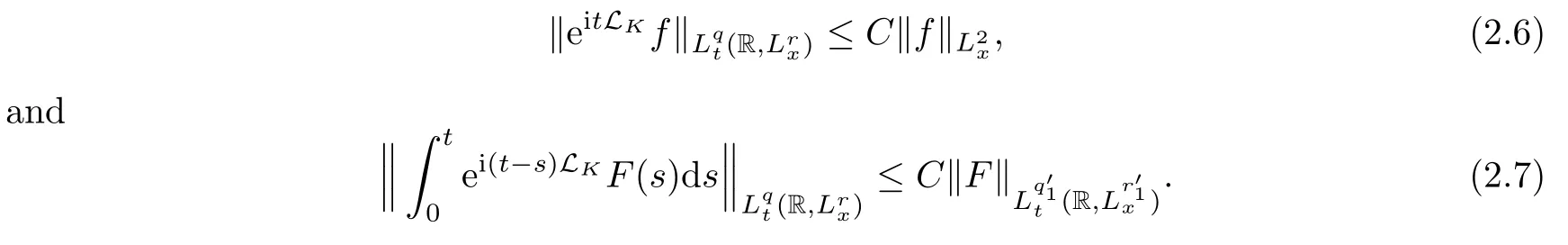
2.3 Fractional Product Rule

2.4 Sobolev Space Equivalence
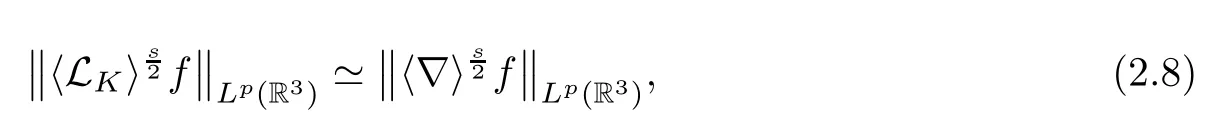

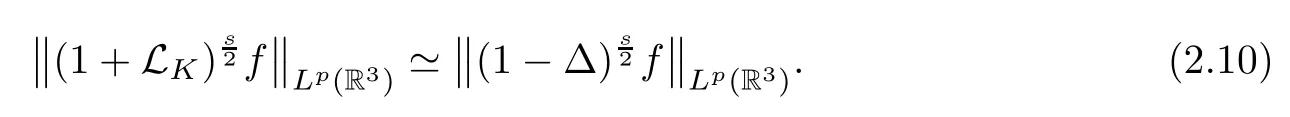

3 Global Well-posedness
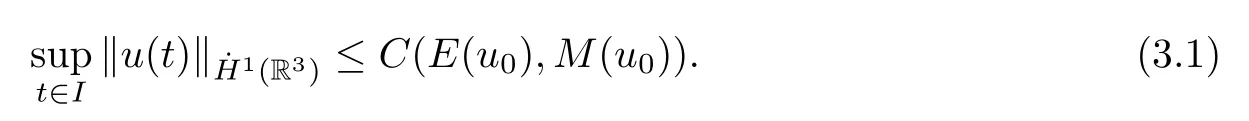
3.1 Local Well-p osed ness for Energy-subcritical:sc<1

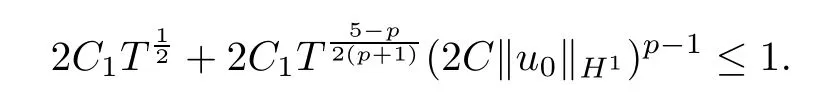
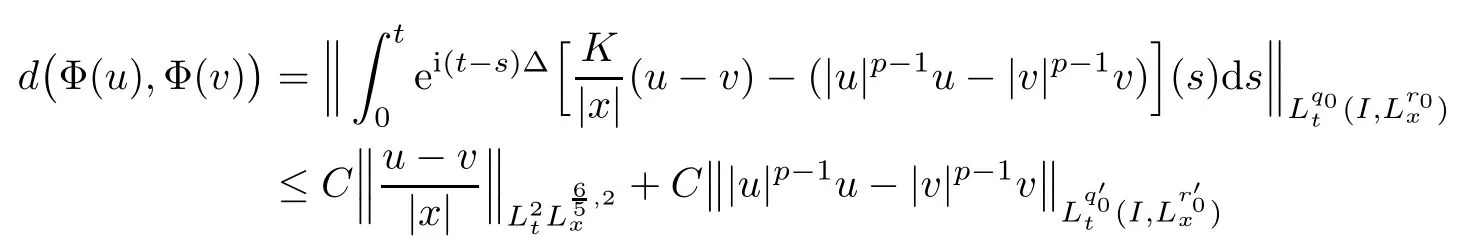
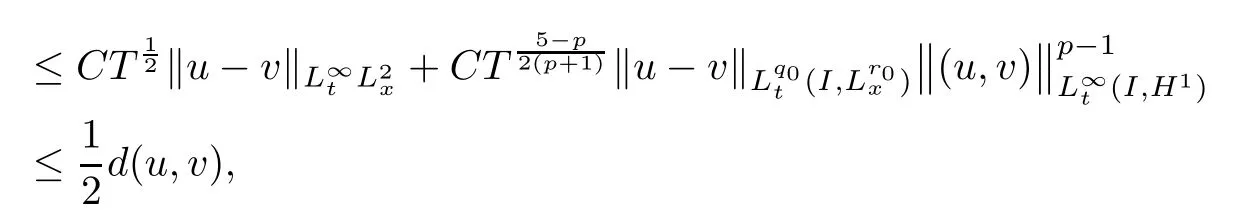
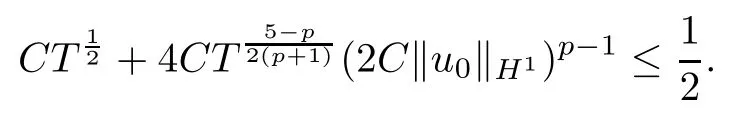
3.2 Global Well-posedness for Energy-subcritical:sc<1
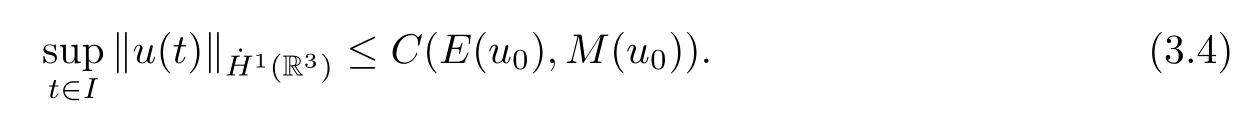
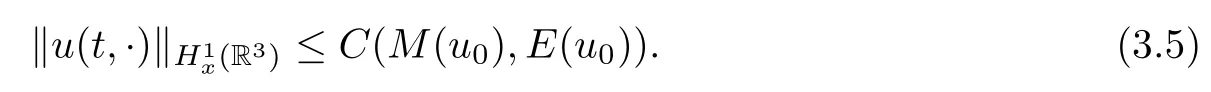


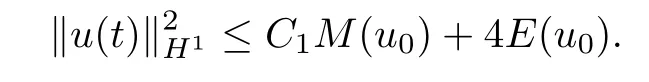
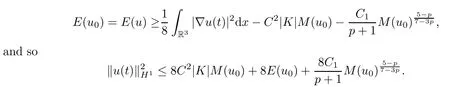
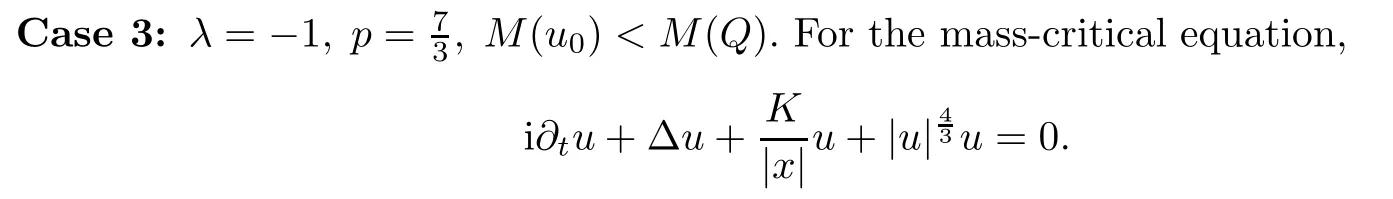
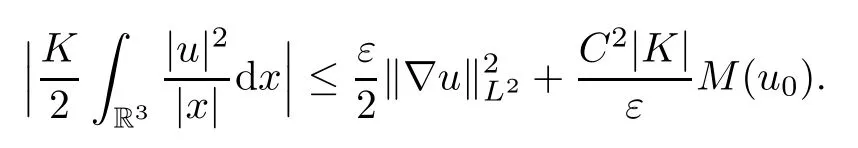
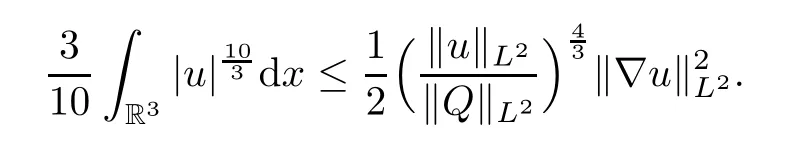
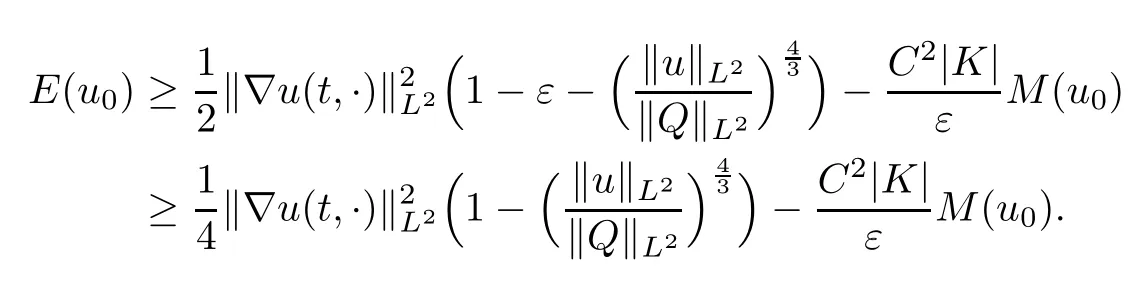
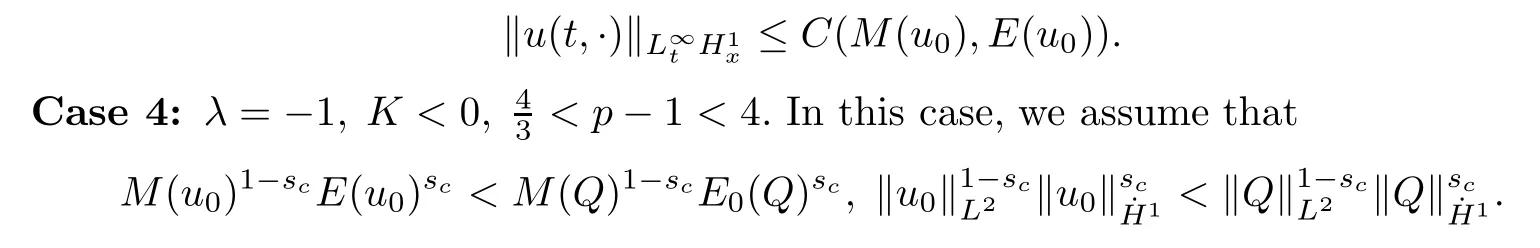
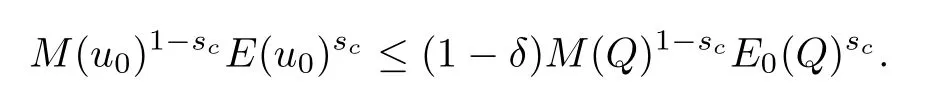

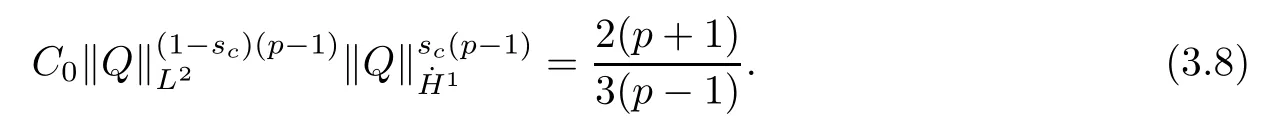
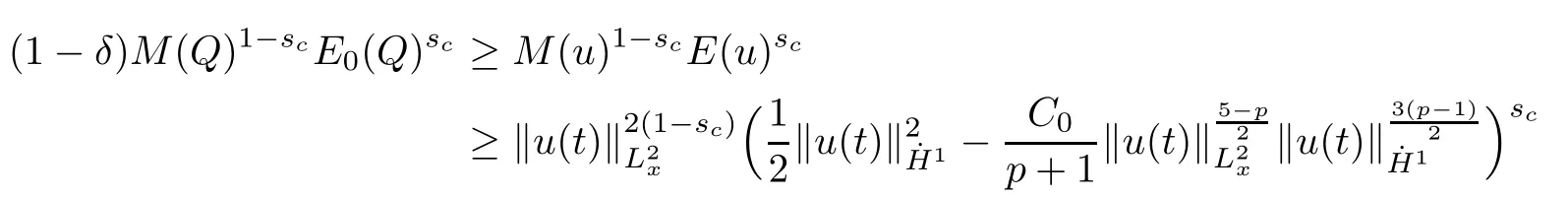


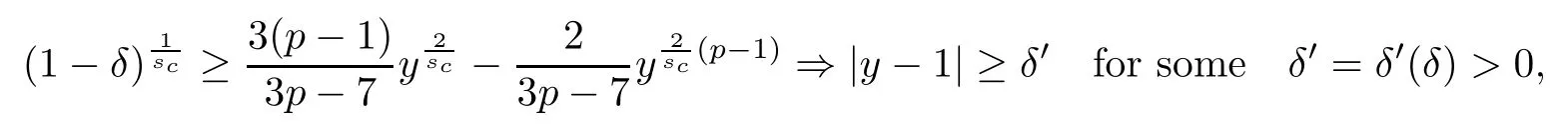


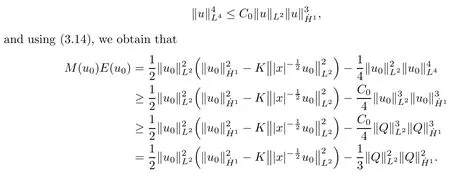
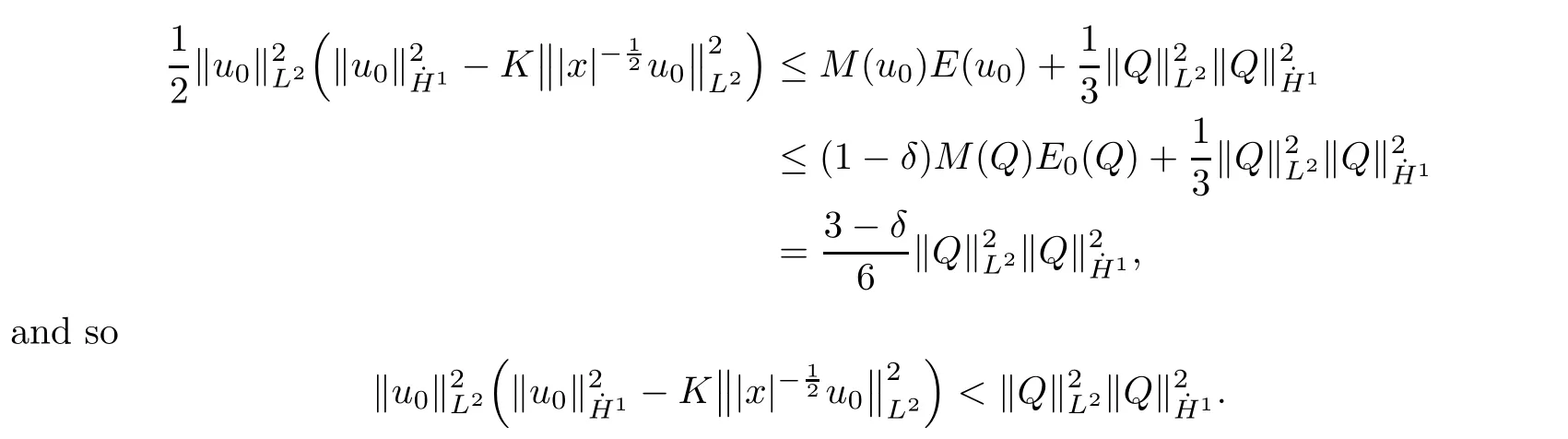


3.3 Global Well-posedness for Energy-critical:sc=1 and K<0
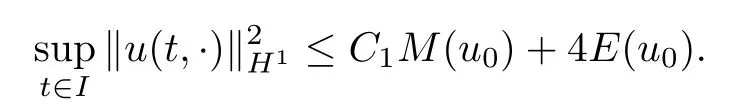
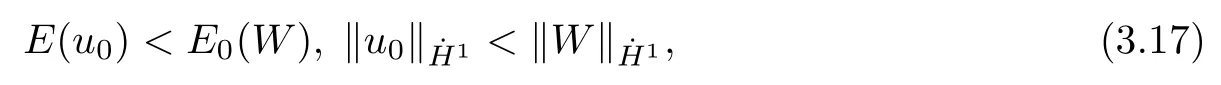
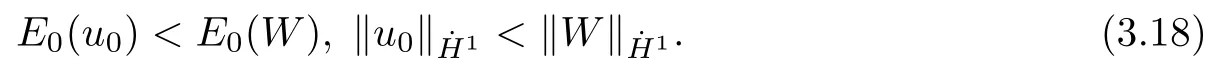
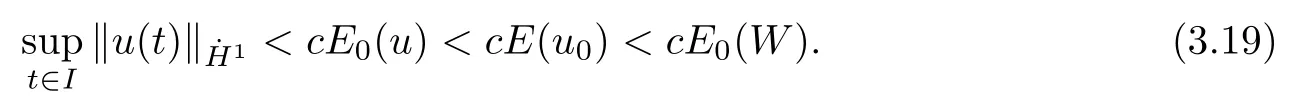
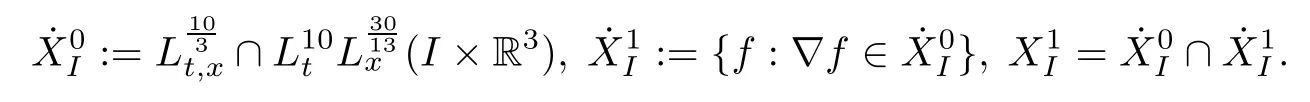
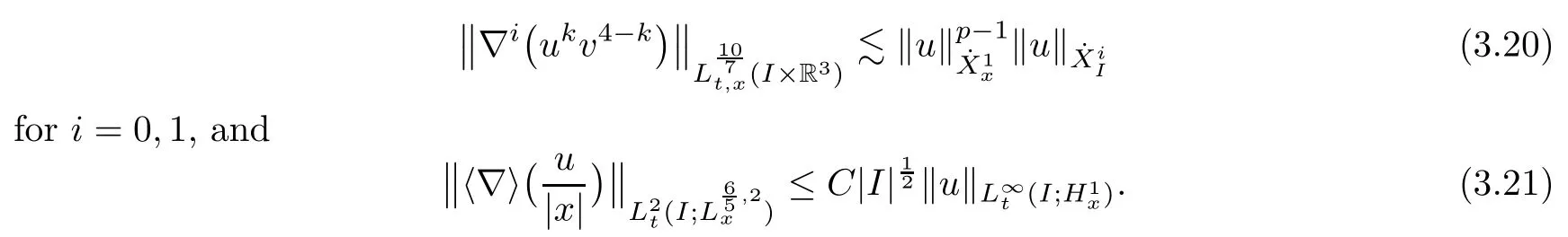
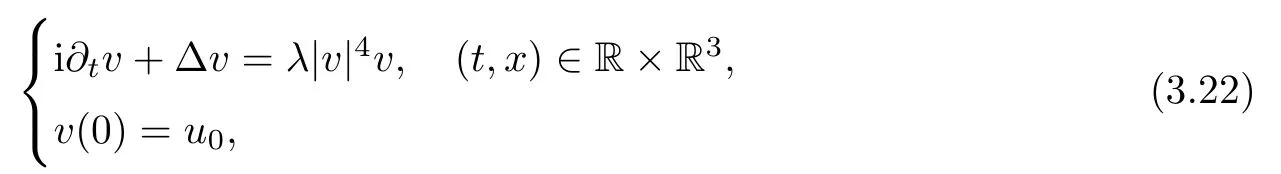
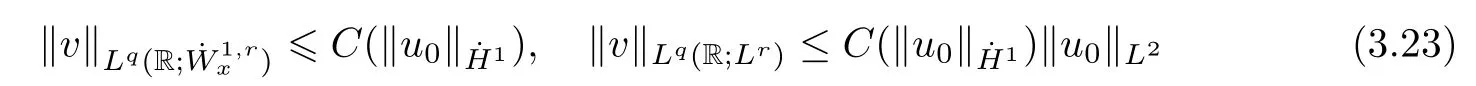

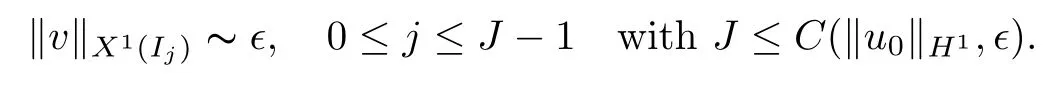
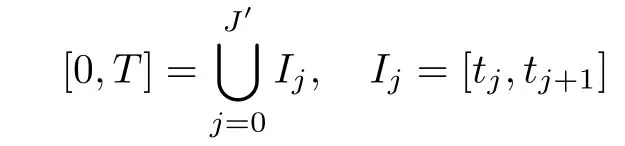

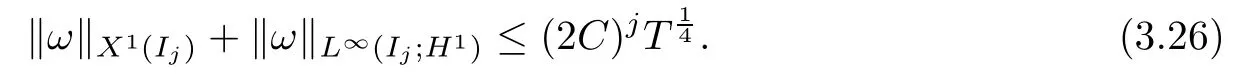



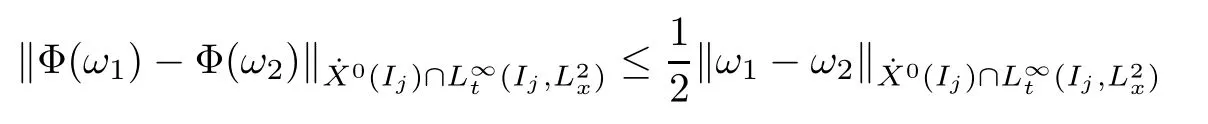

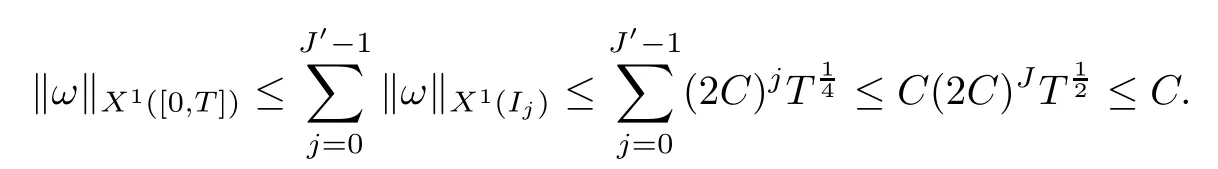
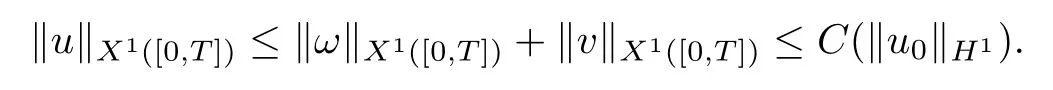
4 Morawetz Estimate and Scattering Theory
4.1 Morawetz Estimate

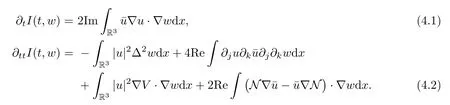

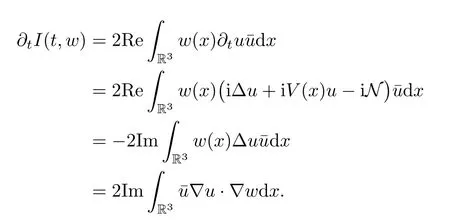
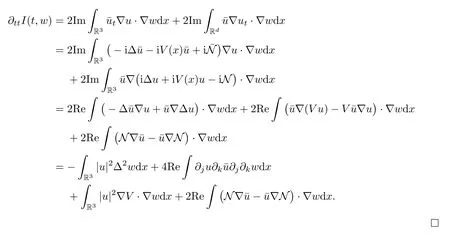


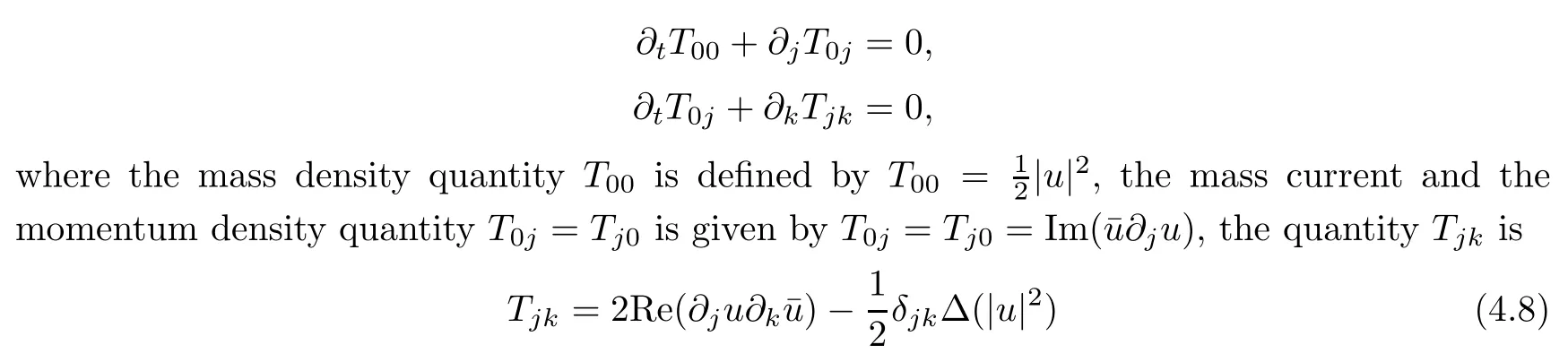

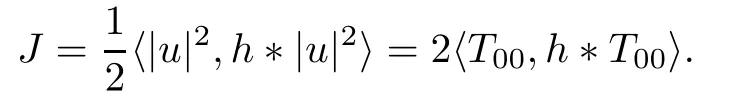


4.2 Scattering Theory


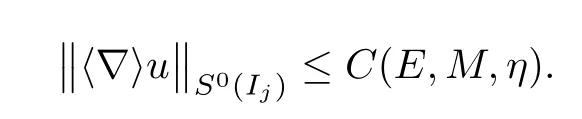





5 Blow up

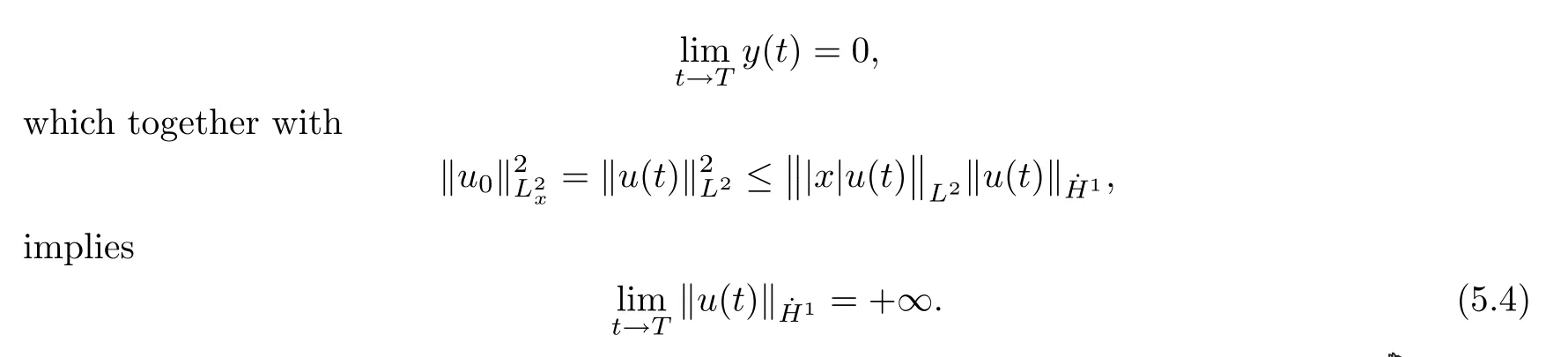

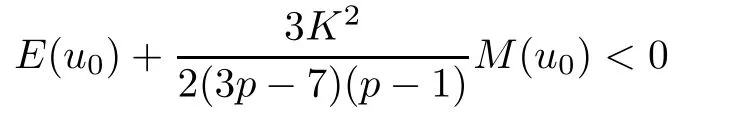
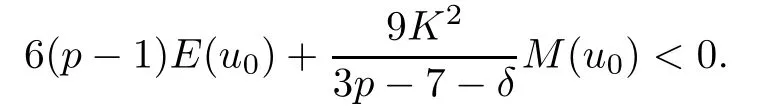
 Acta Mathematica Scientia(English Series)2022年6期
Acta Mathematica Scientia(English Series)2022年6期
