Yunfeng JIANG

College of Mathematics and Statistics,Shenzhen University,Shenzhen 518060,China

Department of Mathematics,University of Kansas,KS 66045,USA

E-mail:y.jiang@ku.edu

Abstract For any scheme Mwith a perfect obstruction theory,Jiang and Thomas associated a scheme N with a symmetric perfect obstruction theory.The scheme N is acone over Mgiven by the dual of the obstruction sheaf of M,and contains Mas its zero section.Locally,N is the critical locus of a regular function.In this note we prove that N is a d-critical scheme in the sense of Joyce.There exists a global motive for N locally given by the motive of the vanishing cycle of the local regular function.We prove a motivic localization formula under the good and circle compact C?-action for N.When taking the Euler characteristic,the weighted Euler characteristic of N weighted by the Behrend function is the signed Euler characteristic of M by motivic method.As applications,using the main theorem we study the motivic generating series of the motivic Vafa-Witten invariants for K 3 surfaces.

Key words motivic Euler characteristics;dual obstructioncone;motivic Vafa-Witten invariants;K 3 surfaces

Dedicated to Professor Banghe LI on the occasion of his 80th birthday

1 Introduction

LetMbe a scheme(or DMstack)with a perfect obstruction theoryE?in the sense of [25],[3].Denote vd=rank(E?),which is the virtual dimension.In [18],Jiang and Thomas associated withMa schemeNwhich admits a symmetric obstruction theory in the sense of Behrend in [1].Roughly,this schemeN=is the total space of the dual of the obstruction sheaf obMassociated with the obstruction theoryE?.For the mathematical definition,

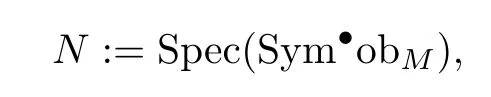
which is the abeliancone of the obstruction sheaf obM.Letπ:N→Mbe the projection.There is a Gm-action onNscaling the fibers,and the fixed locus isM.In [18],the following four invariants were studied:

(1)The Ciocan-Fontanine-Kapranov/Fantechi-G?ttschesigned virtual Euler characteristic ofMdefined using its own obstruction theory;

(2)Graber-Pandharipande’s virtual Atiyah-Bott localization of the virtual cycle ofNtoM;

(3)Behrend’s weighted Euler characteristic ofNby the Behrend functionνN;

(4)Kiem-Li’s cosection localization of the virtual cycle ofNtoM.[18]proves that(1)=(2),and(3)=(4).The invariant(1)=(2)is deformation invariant,while(3)=(4)is not.Moreover,the invariant(3)=(4)is the signed Euler characteristic ofM.A similar situation was studied in [15].It turns out that both of these invariants are useful,and are related to the Vafa-Witten invariants for projective surfaces or local surfaces;see [34],[35].

In the setting of derived algebraic geometry as in [33],Nis(?1)-shifted symplectic because it is the(?1)-shifted cotangent bundleT?(M,E?)[?1]of(M,E?),if(M,E?)comes from a quasi-smooth derived scheme.In [22],Joyce proved that the underlying schemeNof a(?1)-shifted symplectic derived scheme is ad-critical scheme,which is defined in [22].The converse is not true.Since a schemeMwith a perfect obstruction theoryE?is not always induced from a quasi-smooth derived scheme,in the paper [18],the authors started from a derived scheme(M,E?),and constructedNby taking the derived cotangent bundle of(M,E?).

TheconeNadmits a good,circle-compact action of Gmby scaling the fibers ofN.The fixed locus isM.Our main result is as follows:

Our method for proving Theorem 1.1 follows from the argument of the motivic nearby cycle under the good,circle-compact action of Gmin [32].In our situation,Nicaise and Payne [32]proved the conjecture of Davison and Meinhardt on the motivic nearby fiber in [8];i.e.,the motivic nearby cycleWe use this motivic cycle to prove the localization formula.This is parallel to the result in Theorem A.1 of [7],where the author proved that in this situation,the push for ward toMof the vanishing cycle sheafof the local regular functionon ad-critical chart is the shifted constant sheaf onM.Our contribution here is that we prove this statement for the motivic vanishing cycle using the result achieved by Nicaise and Payne in [32]where the techniques of semi-algebraic subsets were employed.Note that we do not need to use the techniques of semi-algebraic sets in [32];we only use the result from there.As an application of Theorem 1.1,we show that

by the motivic method.This equality was proven by a direct topological calculation in [18].

Motivic Vafa-Witten theoryLetSbe a smooth projective surface.Motived by Sduality and Vafa-Witten’s equation in [38],Tanaka-Thomas [34],[35]developed a theory of counting stableand semistable Higgspairs(E,φ),whereEisa torsion freerankrcoherent sheaf onS,andφ:E→E?KSis a OS-linear morphism called the Higgs field.Letrepresent the moduli space of Gieseker stable Higgs pairs with Chern classc=(r,c1,c2)∈H?(S,Z),a fixed determinant det(E)=L,and trace freeφ.In [34],the moduli spacewas proven to be isomorphic to the moduli space of stable two dimensional torsion sheaves compactly supported onX:=Tot(KS).SinceXis a Calabi-Yau threefold(not compact),the moduli spaceadmitsa symmetric obstruction theory in [1].Therefore,there exists a virtual fundamental classThe spaceis not compact,but admits a C?-action scaling the Higgs field,and the fixed locus is compact.The Vafa-Witten invariants are defined by virtual localization

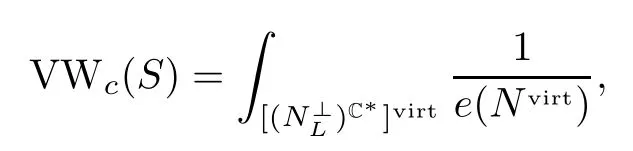
wheree(Nvirt)is the Euler class of the virtual normal bundle.These invariants are called the SU(r)-Vafa-Witten invariants.On the other hand,the following invariants

Definition 1.2

In [36],R.Thomas defined the K-theoretical Vafa-Witten invariantsusing thevirtual structure sheaf and an orientation of the moduli spaces.His invariants are the K-theoretical refi nement of the invariants VW(S).Our motivic Vafa-Witten invariants are only the motivic refinement of the invariants vw(S).They give the same refi nement for K3 surfaces.

From [39],M=ML(S,c0)is an irreduciblesymplectic variety,which isbirational equivalent to the Hilbert scheme Hilbd(S)of point onSwhered=1?χS(c0,c0).We now have to make an assumption.

Assumption 1.3Themotive [M]is isomorphic to the motive [Hilbd(S)]in the Grothendieck ring of varieties.

Remark 1.4Two birational schemes do not in general,need to have the same motives.Thus our assumption above seems not very promising,but from the calculation below our result provides the right calculation result for the generating series.Thus there must exist some mysterious geometries here for the motives [M]and [Hilbd(S)],and these deserve to be explored later.

We have the following result:

Theorem 1.5LetSbe a smooth projective K3 surface.Fix the rankrand the first Chern classc1such that they are coprime.Assume that the Assumption 1.3 holds.Then the motivic generating series of motivic Vafa-Witten invariants is given by

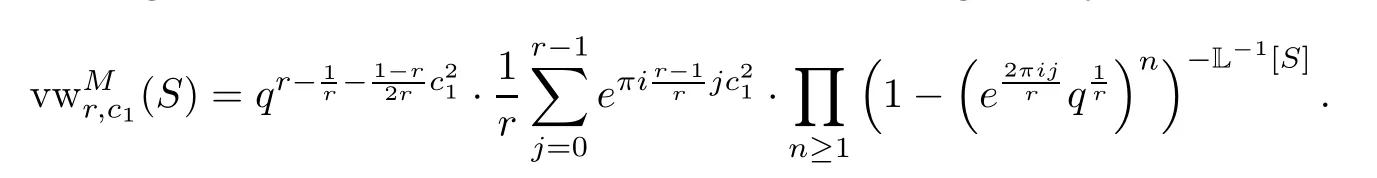
We prove Theorem 1.5 using Theorem 1.1,and reduce the calculation to the general motive ofM.From Yoshioka [39],Mis birational equivalent to the Hilbert scheme of points onS.Everything is reduced to the calculation of the motive of the Hilbert scheme of points onS,and then we use G?ttsche’s result [9].

Recall that there is a ring homomorphisme:K0(VarC)→Z [u,v]from the Grothendieck ring of varieties to Z [u,v]given by the Hodge-Deligne polynomial of varieties.Theχy-genus is juste(y,1);i.e.,u=y,v=1.We define

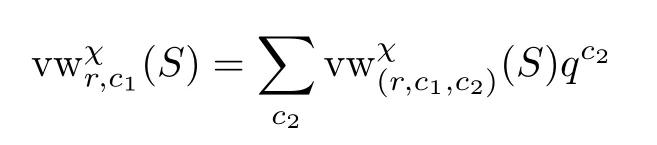
as the generating series of theχy-genus of the Vafa-Witten invariants,where

As a corollary of Theorem 1.5,we calculate theχy-genus.

Corollary 1.6LetSbe a smooth projective K3 surface.Fix the rankrand the first Chern classc1such that they are coprime.Then theχy-genus of the Vafa-Witten invariants is given by

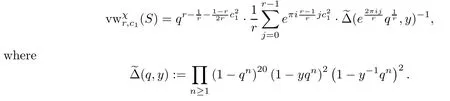
Thus we get a result similar to [36],where R.Thomas used K-theoretical Vafa-Witten invariants to calculate the case of K3 surfaces,and also proved Conjecture 4.6 in [10]using the motivic method.

DiscussionOur motivic series of the Vafa-Witten invariants give the same result as in [36]for K3 surfaces,since for a K3 surfaceS,VW(S)=vw(S).As pointed out in [34],the big Vafa-Witten invariants V W(S)are the correct invariants for the S-duality.This is especially interesting for general type surfaces.

Vafa-Witten actually predicted an S-transformation formula from the gauge group SU(r)to its Langlands dual SU(r)/Zr.In the case of K3 surfaces,the prime rank case was proven in [17],and the higher rank case was studied in [20].The method we use employs the moduli space of optimal gerbe twisted sheaves on K 3 surfaces.The K-theoretical refi nement version of the S-duality implies an S-duality transformation for motivic Vafa-Witten invariants.

OutlineThe rest of the note is organized as follows.In Section 2 we review the construction of the coneN,and prove thatNis ad-critical scheme.We prove a motivic localization formula of the orientedd-critical schemeNunder Gm-action in Section 4,and apply it to get the weighted Euler characteristic of the coneN.Finally,in Section 5 we apply the motivic localization formula to calculate the motivic generating series of the motivic Vafa-Witten invariants for K3 surfaces.

NotationThroughout the paper we work for with a projective schemeMoverκwith a perfect obstruction theoryE?→LM.The one dimensional torus is denoted by Gm.When we work on the motivic Vafa-Witten theory,everything is over C and Gm=C?.

2 Preliminaries on the Cone N

We briefly recall the construction of the abelianconeNin [18].

2.1 Abelian Cones

LetFbe a coherent sheaf overM.There is an associated cone

overM.Cones of this form are called abelian [3,Section 1].The grading on Sym?FendowsC(F)with a Gm-action

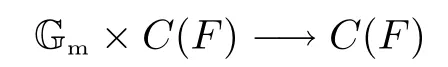
induced by the map

which takess∈SymiFtosxi;its fixed locus is the zero sectionM?C(F)defined by the ideal Sym≥1F.

WhenFis locally free,C(F)=Tot(F?)is the total space of the dual vector bundle.More generally,for anyF,the fibre ofC(F)over a closed pointp∈Mis the vector space(F|p)?.In factC(F)represents the functor fromM-schemes to sets that takef:S→Mto HomS(f?F,OS).

2.2 The Cone N

We fix a perfect obstruction theory

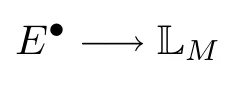
of virtual dimension

on the complex projective schemeM.

Applying the results of the last section to the obstruction sheaf

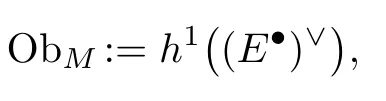
we defineπ=πN:N→Mto be the associated abeliancone,1Another way to describe N is as the coarse moduli space of the vector bundle stackof [3,Section 2].

2.3 Local Model

Locally,we may choose a presentation of(M,E?)as the zero locus of a sectionsof a vector bundleE→Aover a smooth ambient spaceA,such that the resulting complex

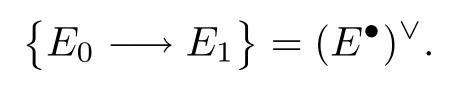
Then we haveE?asE?1→E0,we get the exact sequence

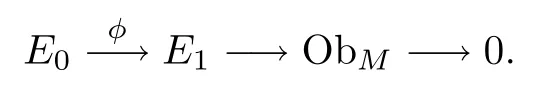
The resolution gives an exact sequence

where we have chosen any holomorphic connectionDonE→Aby shrinkingA,if necessary.

Thinking of the sectionsofE→Aas a linear functionon the fibers of Tot(E?),we find that its critical locus isN.

Proposition 2.1([18,Proposition 2.8])N?Tot(E?)is the critical locus of the function

3 The Global Sheaf of Vanishing Cycles on N

3.1 d-critical Schemes

3.2 Semi-symmetric Obstruction Theory

In this section we review a bit of the semi-symmetric obstruction theory in [5],[16].

Definition 3.2([5,Definition 3.1])A semi-perfect obstruction theory ofNconsists of a covering {Nα}α∈ ΛofNby affine schemes and truncated perfect obstruction theories

such that

(1)for any pairα,β∈ Λ ,there exists an isomorphism

Proposition 3.3([16,Theorem 4.6])There exists a symmetric semi-oerfect obstruction theoryφ={φα,Nα,Eα,ψαβ}α∈ Λfor ad-critical scheme(N,s).

3.3 N is a d-critical Scheme

We show that ourconeNin(2.1)is ad-critical scheme.

Proposition 3.4The schemeNin(2.1)is ad-critical scheme in the sense of [22,Definition 2.5].

3.4 Orientation on d-critical Schemes

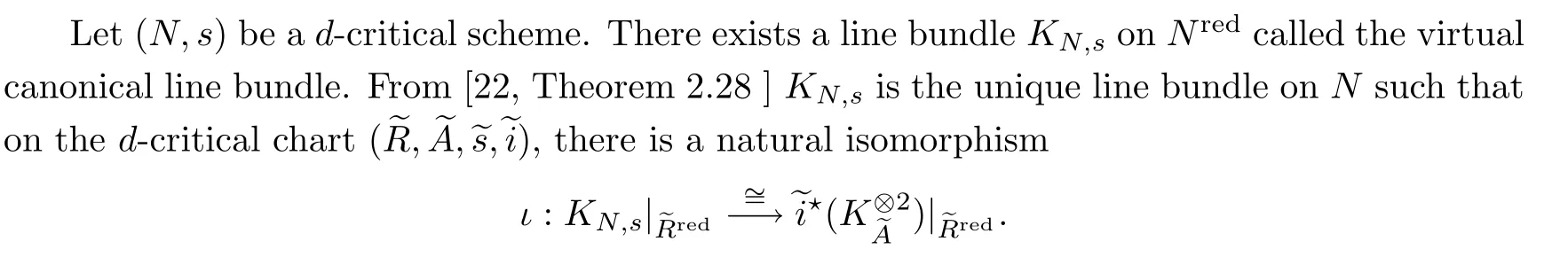
TheconeNin(2.1)admits a Gm-action whose fixed point loci isM?N.As pointed out in [18],it is not known if the schemeNadmits a symmetric obstruction theory of [1],but there is one locally sinceNis the critical locus of a regular function on a higher dimensional smooth scheme.In [18],the authors assumed that the schemeMis the underlying scheme of a quasi-smooth derived scheme,and thatNis the(?1)-shifted cotangent bundle ofM,and therefore admits a symmetric obstruction theory.

From Proposition 3.3,thed-critical scheme(N,s)admits a symmetric semi-perfect obstruction theoryφ={φα,Nα,Eα,ψαβ}α∈ Λas in Definition 3.2.The Gm-action onNinduces an action onφ={φα,Nα,Eα,ψαβ}α∈ Λand makes it a Gm-equivariant symmetric semi-perfect obstruction theory.Note that ifN=We now present a generalization of [36,Proposition 2.6].

Proposition 3.7The canonical line bundleKN,s,when restricted to the fixed point locusM,has a canonical square root such that,for eachα∈ Λ ,

3.5 Motivic Vanishing Cycles

Remark 3.10The orientation in Definition 3.5 for the moduli space of stable coherent sheaves on Calabi-Yau threefolds was constructed in [23].

4 A Motivic Localization Formula

4.1 The General Statement of the Gm-action

Definition 4.1Let(N,s)be ad-critical scheme.A Gm-action

is Gm-invariant ifμ(γ)?(s)=sfor anyγ∈Gm,ands∈H0(SN),or equivalentlyμ?(s)=whereπN:Gm×N→Nis the projection.

Definition 4.2The Gm-action on a schemeNis called good if any orbit is contained in an affine subscheme ofN.Equivalently,there exists an open cover of subschemes which are Gm-invariant.

We now present two results from [22]and [14].

Proposition 4.3Let(N,s)be ad-critical scheme which is Gm-invariant under the Gmaction.Then,

(1)if the actionμis good,then anyx∈Nthere exists a Gm-invariant critical chart(R,U,f,i)on(N,s)such that dim(TxN)=dim(U);

(2)if for allx∈Nwe have a Gm-invariant critical chart(R,U,f,i),the actionμis good.

Let(N,s)be ad-criticalκ-scheme with a good Gm-action.Let

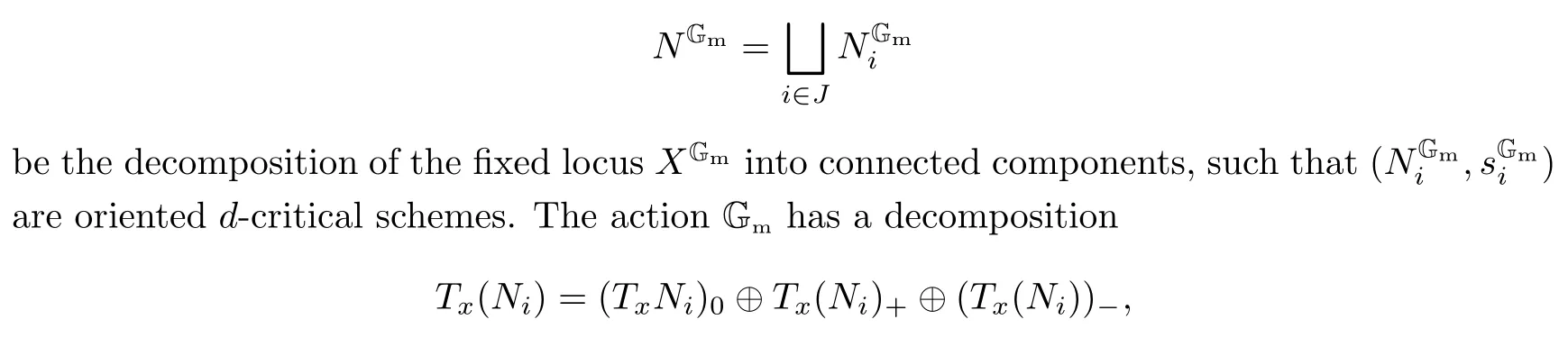
where the direct sums are parts of the zero,positive and negative weights with respect to the Gm-action.Maulik [27]defined the virtual index

Definition 4.5We call the action

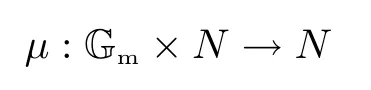
circle-compact if the limit limλ→0μ(λ)xexists for anyx∈N.IfXisproper,then any Gm-action onNis circle-compact.

For thed-critical scheme(N,s)in Proposition 3.4,we have

Proposition 4.6There exists a good and circle compact Gm-action on the orienteddcritical scheme(N,s)for theconeπ:N→M.

4.2 The Gm-localization Formula for the Cone N

Let us consider the invariant

which is one of the main results in [18],and which has applications in the study of Vafa-Witten invariants in [34]and [35].

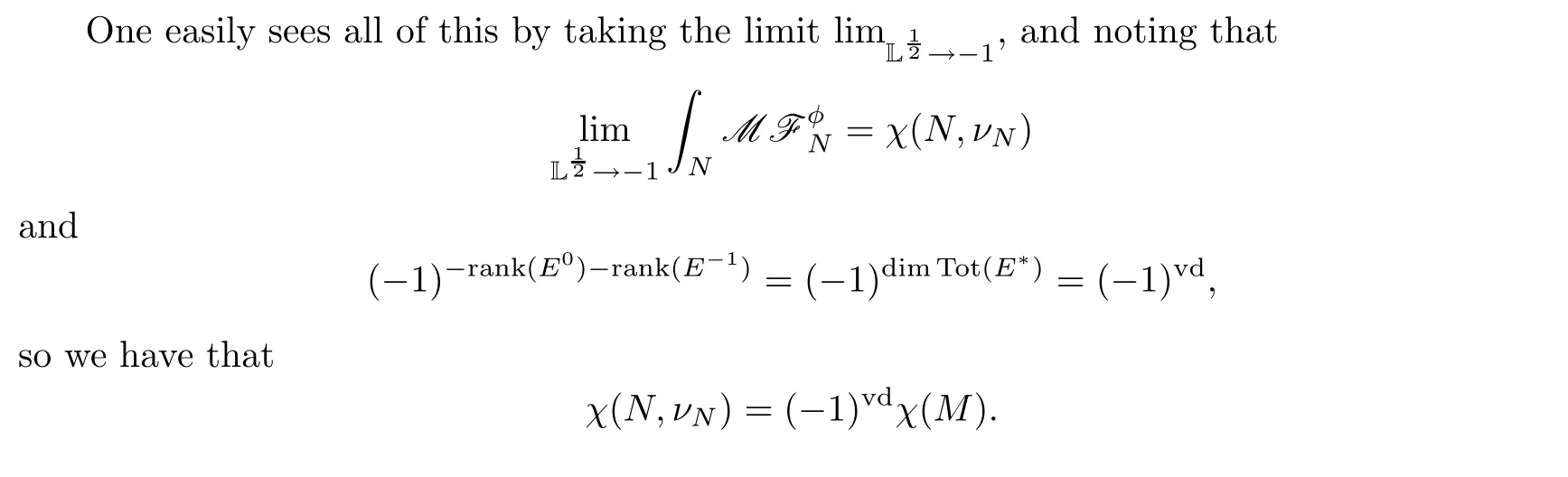
5 Motivic Vafa-Witten Theory

In this section we review the motivic Vafa-Witten invariants and give calculations for K3 surfaces.

5.1 Power Structure on Motivic Ring

We recall the power structure on the Grothendieck ringK0(Varκ)following [12].LetRbe a ring.A power structure onRis a map

which satisfies the propertiesA(q)0=1,A(q)1=A(q),A(q)m+n=A(q)mA(q)n,A(q)mn=(A(q)m)n,A(q)mB(q)m=(A(q)B(q))m,and(1+q)m=1+mq+O(q2).From [12],there exists a power structure on the GrothendieckringK0(VarC),defined uniquely by the property that,for a varietyX,

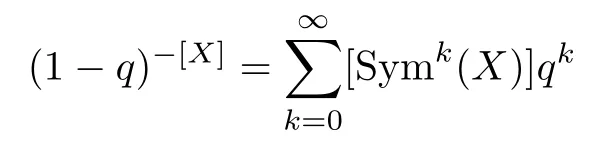
is the motivic zeta function.

Also from [12]we have the exponential map

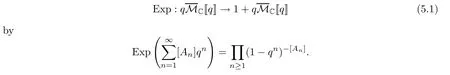
This equation satisfies the substitution rule:

5.2 Motivic Vafa-Witten Invariants

In this section we define the motivic Vafa-Witten invariants.Let us fix a smooth surfaceSandX:=Tot(KS)to be the total space of the canonical line bundleKS.In [34],Tanaka-Thomas defined the moduli space of stable Higgs pairs(E,φ),whereEis a torsion free rankrcoherent sheaf onS,andφ:E→E?KSis a OS-linear map called the Higgs field.The detailed definition of the Gieseker stability and the construction of the moduli spaces are presented in [34].We work on the moduli space

of stable Higgs pairs onSwith topological invariantsc=(r,c1,c2)and tr(φ)=0,det(E)=L∈Pic(S).From the spectral theory in [34,§2],every Higgs pair(E,φ)corresponds to a two dimensional torsion sheaf Eφsupported onS?X.The Gieseker stability of the Higgs pair(E,φ)transforms to the Gieseker stability of the torsion sheaf Eφ,and the moduli spaceis isomorphic to the moduli space of stable two dimensional torsion sheaves onXwith a fixed determinant.Thus the moduli spaceadmits a symmetric obstruction theory as in [1].is not compact,but admits a C?-action scaling the Higgs field(or induced by the scaling fiber action onX),and the C?-fixed locus contains two branches.

Instanton BranchThe first component contains Higgs pairs(E,φ)which are C?-fixed andφ=0.This component is just the moduli spaceM:=ML(S,c)of stable coherent sheaves onSwith the topological invariantc.Note that in this caseEis stable.

Monop ole BranchThe second component contains Higgs pairs(E,φ)which are C?-fixed andφ0.This component usually contains pair(E,φ),whereEsplits into direct sum of subsheaves which may be nonsemistable.For general type surfacesSwithpg>0,some component in this loci is isomorphic to the nested Hilbert schemes onS;see [34]and [36].

The SU(r)-Vafa-Witten invariants are defined by virtual localization [11]by

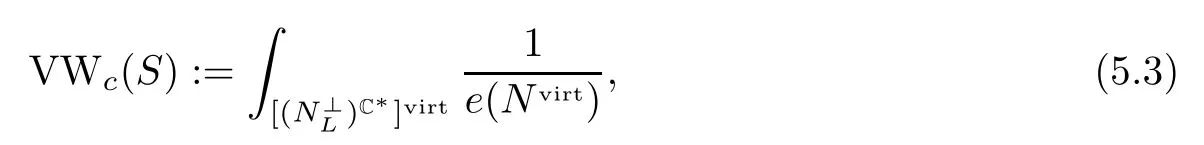
wheree(Nvirt)is the Euler class of the virtual normal bundle.The small SU(r)-Vafa-Witten invariants are defined by

where the integral means pushing forward to a point.

Remark 5.2The motivic Vafa-Witten invariants can only be defined as a refinement for the invariants vw(S).In [36],R.Thomas defined the refi nement K-theoretical Vafa-Witten invariants using the virtual structure sheaf and an orientationwhich refined the Vafa-Witten invariants VW(S).

In order to apply Theorem 4.7,let

The C?-fixed locus ofNisM=ML(S,c).We review the splitting of the perfect obstruction theory ofNonMa bit here following [34,§3].Let

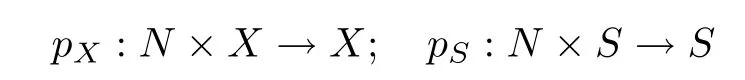
be the projections and let E onN×Xbe the universal sheaf(or Higgs pair).Letπ:N×X→N×Sbe the projection.Then the pushforwardπ?E=E is the universal sheaf onN×S.Then,from the diagram in([34,Corollary 2.22]),

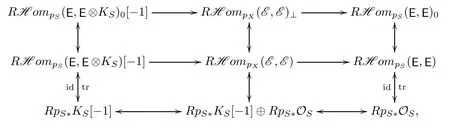
where t?1represents the moving part of the C?-action,which is the standard representation of C?.Then

Remark 5.3Taking the Euler characteristic of(5.5)gives that

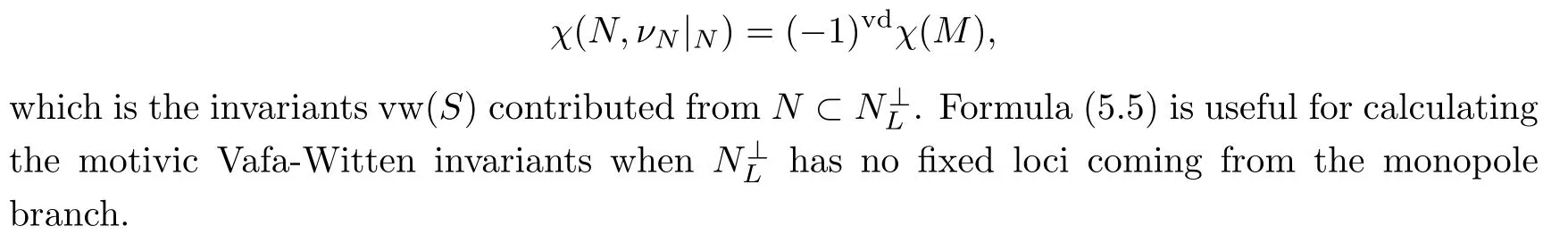
5.3 Proof of Theorem 1.5-Calculations for K 3 Surfaces

LetSbe a smooth projective K3 surface.In this section we perform a calculation for the motivic invariants forS.In this case,X=S×C,and any C?-fixed Higgs pair(E,φ)has a vanishing Higgs fieldφ=0.Therefore the moduli spaceN=→Mis acone over the moduli space of stable sheavesM.We only have the instanton branch.

Fix a topological invariantc0=(r,c1,c2)∈H?(S,Z)such that(r,c1)=1.Then semistablity coincides with stability and the moduli spaceM=ML(S,c0)is an irreducible symplectic variety which is birational equivalent to the Hilbert scheme Hilbd(S)of point onS(see [39]).Here

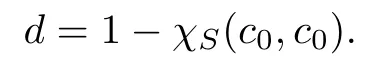
Since the moduli spaceM=ML(S,c0)is smooth,its virtual dimension is

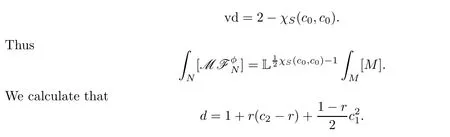
Thus,from Assumption 1.3,we write down the motivic generating series as

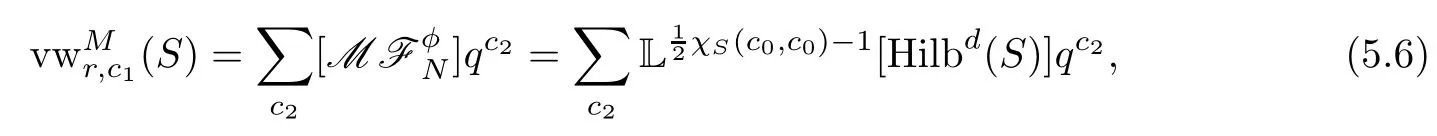
We calculate the motivic series(writec2as integersm∈Z)as

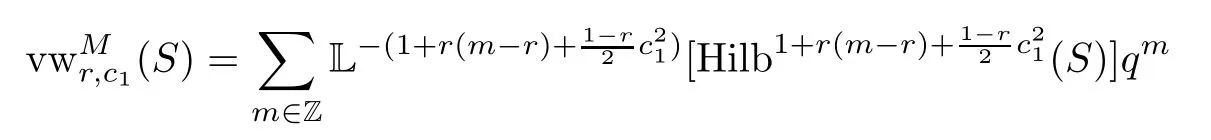
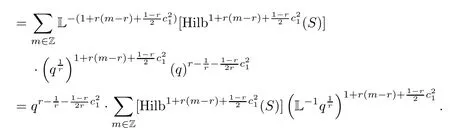
Now,using the exponential form(see [2,9,12]),

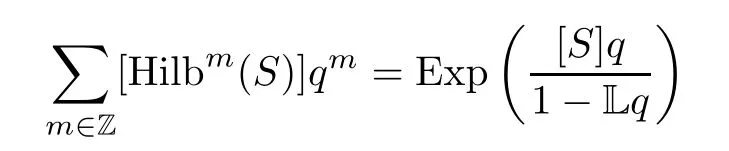
and therefore,

Then we have that

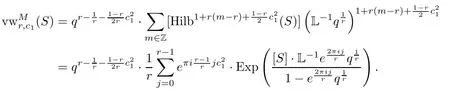
We also can write this in the infinite product form.From(5.1),and since

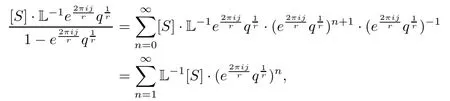
and we have that

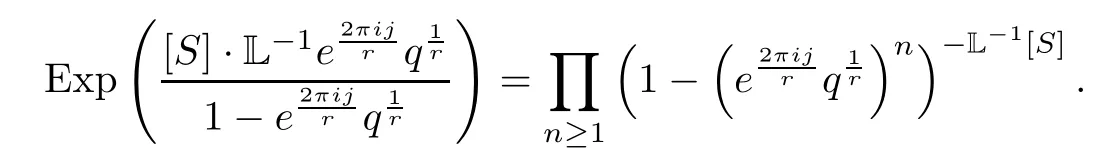
Then,

5.4 Proof of theχy-genus in Corollary 1.6

From [12],there exists a ring homomorphism

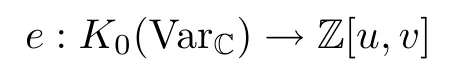
given by sending each varietyXto its Hodge-Deligne polynomial

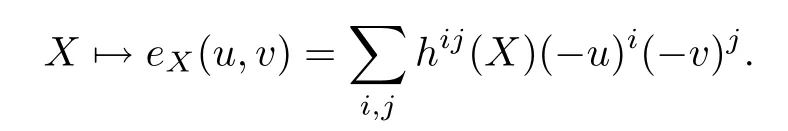
Theχy-genus is justeX(y,1).Theχy-polynomial of the K 3 surfaceSisχy(S)=2+20y+2y2.For the Hilbert scheme Hilbm(S),from the properties of the ring homomorphism in [12,Theorem 2],we have that

We define

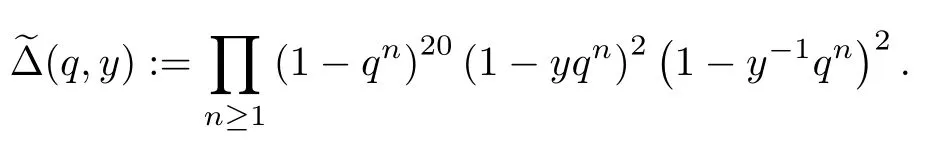
Then we get theχy-genus of the Vafa-Witten invariants

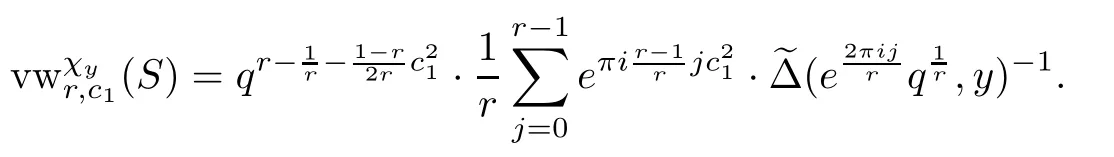
Note that this result is similar to [36,Theorem 5.48],where Thomas used the K-theoretical Vafa-Witten invariants.

Acknow ledgementsThis paper was motivated by the study by Tanaka-Thomas [34],[35]on the Vafa-Witten invariants for projective surfaces.I would like to thank R.Thomas for sending me the above papers before posting on ar Xiv.Many thanks to B.Szendroi for the valuable discussion on motivic invariants of Hilbert schemes of points on C3,and S.Payne for the discussion on motivic nearby cycles and motivic Minor fibers via semi-algebraic sets.Y.J.is partially supported by a Simon Foundation Collaboration Grant.