單 墫

(南京師范大學數(shù)學科學學院,210023)

解析幾何中的坐標平移,簡明清晰,解題時常可以用來化繁為簡,而且體現(xiàn)了運動與變換,應當引入教材.

以2022年新高考為例,一個例子是今年新高考全國I卷第21題,原題如下.

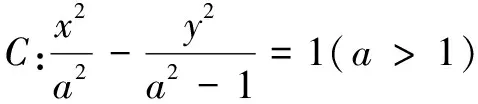
(1)求l的斜率;

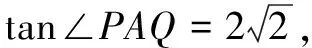
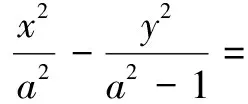
x2-2y2=2.

①

更一般地,考慮點A(x0,y0),曲線C:px2+qy2=t.作坐標平移

則在uv平面中,A為原點,而C的方程變?yōu)?/p>

p(u+x0)2+q(v+y0)2=t,

展開為

pu2+qv2+ru+sv=0,

②

因為曲線C過原點A,所以② 式中的常數(shù)項為0,不必計算,而r=2px0,s=2qy0.

設直線l的方程為mu+nv=1,則有齊次方程

pu2+qv2+(ru+sv)(mu+nv)=0,

③

它表示過原點A的直線AP,AQ.

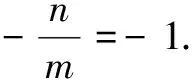
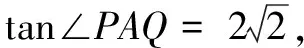
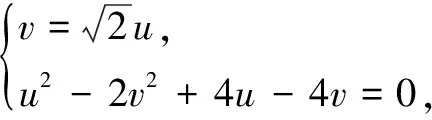
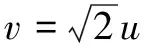
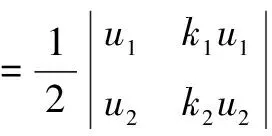
另一個例子是今年新高考全國乙卷第20題,很多人反映計算量大，其實作一個平移即可化繁為簡.

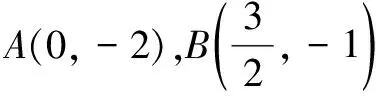
(1)求橢圓E的方程;

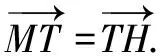
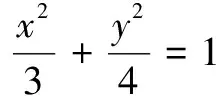
(2)令v=y+2,平移x軸以A(0,-2)為新的原點.則在xv坐標系中,E的方程為4x2+3(v-2)2=12,即

4x2+3v2-12v=0.

④

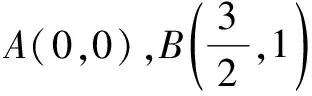
3v=2x,

⑤

設過點P(新坐標為P(1,0))的直線方程為

x=hv+1.

⑥

M,N兩點的坐標(x1,v1),(x2,v2)滿足④ 和⑥ 式,所以也滿足4(hv+1)2+3v2-12v=0,即

(4h2+3)v2+(8h-12)v+4=0.

⑦

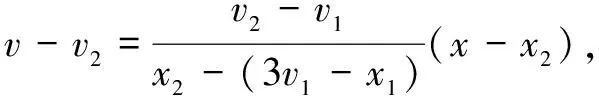
而v2(3v1-x1)-x2v1

=3v1v2-x1v2-x2v1

=(3-2h)v1v2-(v1+v2)

=0,

所以直線HN過點A(定點).

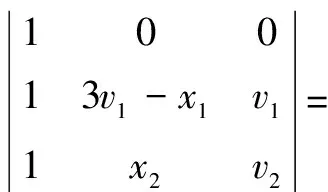
真不明白編課程標準的人為什么不將坐標平移列入課程.