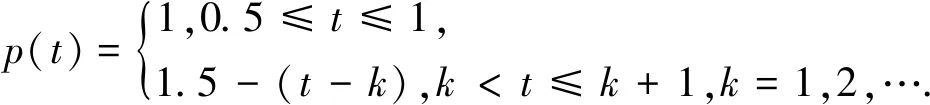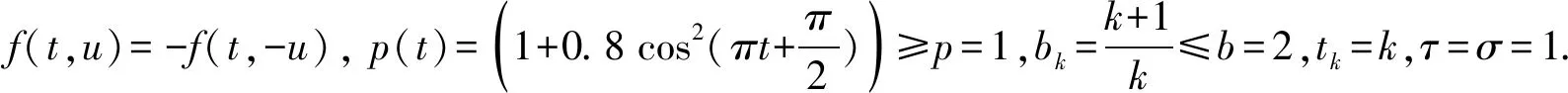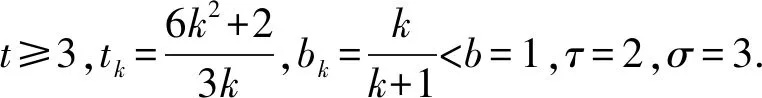一階非線性中立型脈沖微分方程解的振動性
韋晶晶, 申建華
(杭州師范大學數(shù)學學院,浙江 杭州 311121)
0 前言
眾所周知,脈沖微分方程是研究動力學過程中狀態(tài)突然發(fā)生變化的基本模型.在過去的幾十年中,脈沖微分方程已被廣泛研究.關于時滯微分方程和中立型時滯微分方程解性質(zhì)的研究工作已十分豐富[1-9].文獻[10-18]研究了脈沖擾動下時滯微分方程解的振動性.
文獻[12]考慮了系統(tǒng)
(1)
得到了關于系統(tǒng)(1)所有解振動的充分條件.
文獻[14]在文獻[12]的基礎上,研究了如下一階中立型時滯微分方程
(x(t)-p(t)x(t-τ))′+q(t)G(x(t-σ))=0,t≠tk,t≥t0
(2)
本文的目的是研究如下中立型脈沖微分方程

(3)
解的振動性,其中假設后面的條件(A)成立.為此先給出有關定義與假設.
定義1設I,J?,稱函數(shù)φ:I→J屬于PC(I,J),如果滿足:


定義2實值函數(shù)x(t)被稱作是系統(tǒng)(3)的解,如果滿足:


系統(tǒng)(3)的解如果最終為正或者最終為負,則稱解是非振動的.否則就稱系統(tǒng)(3)的解為振動的.
假設如下條件(A)成立:
(A1)對t≥t0,f(t,u)關于u∈是奇函數(shù),即f(t,-u)=-f(t,u);
(A2)存在g(t)≥0,G(u)>0, 使得f(t,u)≥g(t)G(u)對任意u>0和t≥t0成立;
(A3)τ∈(0,∞),σ∈(0,∞),p(t)∈PC([t0,∞),+),其中+=[0,∞). {tk} 是一個嚴格單調(diào)增加的正實數(shù)序列,滿足0≤t0 (A4)G是非增的,對u≠0,有uG(u)>0.那么,存在一個常數(shù)L>0,使得|G(u)|≥L|u|,u∈.事實上,G可以寫成G(u)=u(L+|u|μ),u∈,μ>0. 本節(jié)將給出一些引理,并運用這些引理得出系統(tǒng)所有解振動的充分條件.其中引理2的證明思想?yún)⒖嘉墨I[12],但是文獻[12]在對l個脈沖點進行排列后,并未考慮左端點t是否為脈沖點,這對于接下來證明過程中z(t)的單調(diào)性是否適用起著關鍵性的作用.本文對t是否為脈沖點的兩種情況加以討論,相較文獻[12]更加嚴謹. 引理1假設條件(A)滿足,存在一個序列{sn},使得對任意的n=1,2,…,有sn∈(tn,tn+1],sn+1-sn=τ,p(sn)>0,且 (4) 進一步,假設 (5) (6) z(t)=x(t)-p(t)x(t-τ), (7) 證明由(A4)和(7),有 z′(t)=-f(t,x(t-σ)≤-g(t)G(x(1-σ))≤-Lg(t)x(t-σ),tk (8) 首先有z(tk)≥0,k≥1.否則一定存在某個m≥1,使得z(tm)<0.由式(7),有 對k∈K1k,根據(jù)式(5)有 對k∈K2k,根據(jù)式(6)有 bkx(tk)-bkp(tk)x(tk-τ)=bkz(tk). 因為K1k∪K2k={1,2,…},由此可得 (9) 通過歸納,不難得到 從而,當n=1,2,…,式(7)意味著 x(sm+n)=z(sm+n)+p(sm+n)x(sm+n-1)≤ -bmbm+1…bm+nμ+p(sm+n)x(sm+n-1)≤ -bmbm+1…bm+nμ-p(sm+n)bmbm+1…bm+n-1μp(sm+n)p(sm+n-1)bmbm+1…bm+n-2μ-…- p(sm+n)p(sm+n-1)…p(sm+2)bmbm+1μ-p(sm+n)p(sm+n-1)…p(sm+2)p(sm+1)x(sm)= 這與事實z(tm+1)>0矛盾.從而,對t∈(tk,tk+1],k=0,1,2,…,有z(t)≥z(tk+1)>0.因此,z(t)>0 對任意t≥t0成立.引理證畢. 引理2引理1中所有假設都滿足.此外,假設存在p∈(0,1],b>0,a>0,使得 p(t)≥p,bk≤b,tk+1-tk≥α,k=1,2,…. (10) 假設系統(tǒng)(3)有一解x(t),且x(t-σ)>0,t≥t0.令T=max{t0+σ,t0+τ},m=min{k:tk>T}.那么二階脈沖微分不等式 (11) t 由式(8)和(9)有 如果t不是脈沖點,即t≠ti-1,那么 z(t)(ti-t)+biz(ti)(ti+1-ti)+…+bi…bi+lz(ti)(t+τ-ti+l)≤ z(t)(ti-t)+biz(t)(ti+1-ti)+…+bi…bi+lz(t)(t+τ-ti+l)≤ z(t)(ti-t)+bz(t)(ti+1-ti)+…+bl+1z(t)(t+τ-ti+l)≤ 如果t是脈沖點,即t=ti-1,那么一定有t≥t1,也就是i-1≥1.又bk≤b,對k=1,2,…成立,從而可知bi-1≤b.此時, bi-1z(ti-1)(ti-t)+biz(ti)(ti+1-ti)+…+bi+lz(ti+l)(t+τ-ti+l)≤ bi-1z(ti-1)(ti-t)+bi-1biz(ti-1)(ti+1-ti)+…+bi-1…bi+lz(ti-1)(t+τ-ti+l)≤ bz(t)(ti-t)+b2z(t)(ti+1-ti)+…+bl+2z(t)(t+τ-ti+l)≤ 令M=min{x(t):t0-τ≤t≤t0},對t∈(t0,t0+τ],有 對t∈(t0+τ,t0+2τ],有 通過歸納,對于t∈(t0+nτ,t0+(n+1)τ],有 因此,對于t∈(t0,∞),有 (12) 下面,分兩種情況討論. 情況Ⅰσ>τ. 對t>t0+σ,有 又t0≥0,上面的不等式可表示成 (13) s-σ+τ 根據(jù)式(8)和式(9),當s-σ+τ≠tk-1時,有 b-q-1z(s). 當s-σ+τ=tk-1時,有 b-q-2z(s). 因而有z(s-σ+τ)≥b-q-1z(s).聯(lián)立式(13),可知 將上式代入到(8)中,看到 令 那么下面這個不等式成立 情況Ⅱσ≤τ. 對t>t0+τ,有 又t0≥0,上面的不等式可表示成 將上式代入到(8)中,看到 令 那么下面的不等式成立 綜上,此引理得證. 引理3[12]考慮脈沖微分不等式 (14) 其中0≤t0 那么不等式(14)不存在這樣的解x(t)使得對t>t0,有x(t)>0且x′(t)>0. 引理4[18]p(t)是分段函數(shù),若 (15) 則不等式x′(t)+p(t)x(t-σ)≤0無最終正解. 在下面的定理1至定理3中,假設引理1的條件都滿足. 定理1假設tk+1-tk≥α>0,k=1,2,….如果 (16) 那么系統(tǒng)(3)的所有解都是振動的. 證明運用反證法,假設系統(tǒng)(3)有非振動解x(t).不失一般性,假設對任意t>t0,有x(t)>0,x(t-ρ)>0.即x(t)是系統(tǒng)(3)的最終正解.若x(t)是系統(tǒng)(3)的最終負解,根據(jù)假設知-x(t)則是系統(tǒng)的最終正解,證明過程相似.因而證明中不再贅述. 由引理1可知,對任意t∈(tk,tk+1],k=0,1,2,…,有z(t)>0.現(xiàn)考慮以下兩種情況: 情況Ⅰσ≥α>0. 此時 z′(t)=-f(t,x(t-σ))≤-Lg(t)x(t-σ)≤0. (17) 將上式從tk到tk+α積分,有 又z(t)=x(t)-p(t)x(t-τ)≤x(t). 因而 (18) 由于tk-σ<η-σ≤tk+α-σ≤tk, 式(18)可表示成 如果條件(16)滿足,那么將產(chǎn)生矛盾.此種情況下系統(tǒng)的所有解振動. 情況Ⅱ0<σ<α. 對式(17)從tk到tk+σ積分,又z(t)≤x(t),有 (19) 由于tk-α≤η-σ≤tk,式(19)可表示成 如果條件(16)滿足,那么將產(chǎn)生矛盾.此時系統(tǒng)的所有解振動. 綜上,滿足定理條件的系統(tǒng)(3)的所有解都振動.此定理證畢. 定理2假設存在常數(shù)p∈(0,1],b>0和α>0,使得對任意t≥t0,有p(t)≥p,bk≤b和tk+1-tk≥α,其中k=1,2,….并且存在函數(shù)f(t)∈PC([t0,∞),R+),滿足 (20) 其中T=max{t0+σ,t0+τ},m=min{k≥1:tk>T},且 此時,系統(tǒng)(3)的所有解振動. 證明運用反證法,假設系統(tǒng)(3)有非振動解x(t).不失一般性,假設對任意t>t0,有x(t)>0,x(t-ρ)>0.即x(t)是系統(tǒng)(3)的最終正解.接著,由引理2看到二階脈沖微分不等式 (21) 另一方面,根據(jù)引理3不難看出,式(20)滿足意味著不等式(21)沒有這樣一個解x(t),使得對t>T有x(t)>0,x′(t)>0.這產(chǎn)生了矛盾,也就是說系統(tǒng)(3)的所有解振動.此定理得證. 定理3假設存在常數(shù)b>0,使得對任意t≥t0,有bk≤b.假設tk+1-tk≥α>0,k=1,2,….如果 (22) 證明假設系統(tǒng)(3)有一個最終正解x(t),且對t≥T>t0有x(t)>0,x(t-ρ)>0.根據(jù)引理1知道z(t)>0且z(t)在(tk,tk+1],k=1,2,…上非增. 0=z′(t)+f(t,x(t-σ))≥z′(t)+Lg(t)x(t-σ)≥ z′(t)+Lg(t)(z(t-σ)+p(t-σ)x(t-σ-τ))≥ z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ-τ)) 下面對t-σ是否為脈沖點進行討論. 第一種情況,t-σ是脈沖點. 當τ<α時,有 0=z′(t)+f(t,x(t-σ))≥z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ)), 因此 z′(t)+Lg(t)(z(t-σ)+p(t-σ)z(t-σ))≤0 (23) 有一最終正解. 當τ≥α時,至少存在[τ/α]=l個脈沖點,使得 此時 (24) 有一最終正解. 第二種情況,t-σ不是脈沖點. 當σ+τ<α時,同樣得到式(23).當σ+τ≥α時,同樣得到式(24). 根據(jù)引理4易知,當條件(22)滿足時,式(23),(24)都沒有最終正解.這產(chǎn)生了矛盾,也就是說假設不成立.因此,系統(tǒng)(3)的所有解是振動的.定理得證. 例1考慮脈沖微分方程 (25) 易見 因而,式(25)滿足引理1中所有條件. 又tk+1-tk=1≥α>0,令α=1,此時ζ=min{2,1}=1. 根據(jù)定理1,知道系統(tǒng)(25)的所有解都振動. 例2考慮脈沖微分方程 (26) 易見 因此,引理1的所有條件都滿足.令 考慮 其中G(t)的計算如下: 顯然式(20)滿足,從而根據(jù)定理2,知道系統(tǒng)(26)的所有解都振動. 例3考慮脈沖微分方程 (27) 有 此外, f(t,u)=(2+t+u2)u(1+|u|2)≥(2+t)u(1+|u|2)≥g(t)G(u),u>0. 這里g(t)=2+t.易見f(t,u)=-f(t,-u),因此引理1的所有條件都滿足.對于任意的t>T,即t>6,有 根據(jù)定理3,系統(tǒng)(27)的所有解振動.1 引理和主要結果

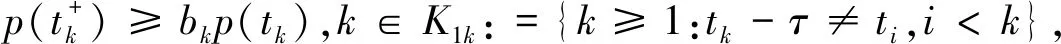
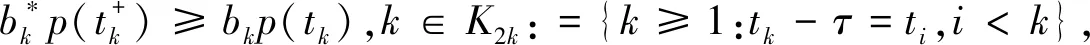










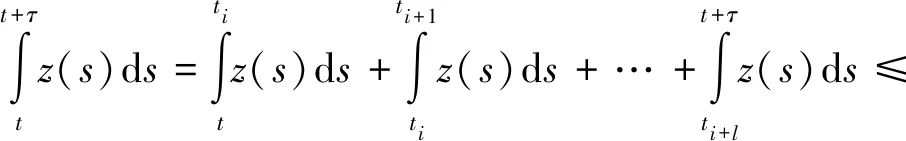


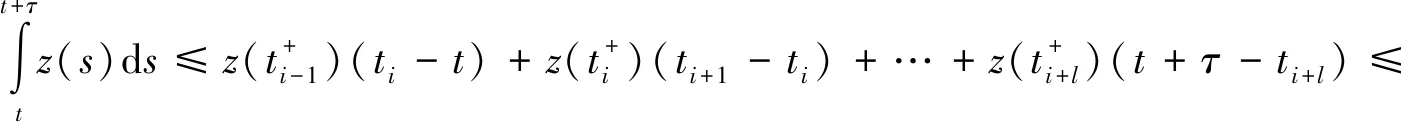










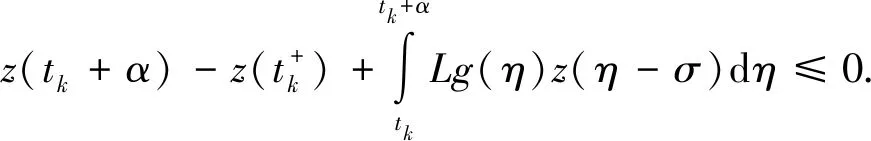







2 應用舉例