Axial effect analysis of relativistic electron beam propagation in vacuum
Xi WANG (王希),Jianhong HAO (郝建紅),Fang ZHANG (張芳),Qiang ZHAO (趙強),Jieqing FAN (范杰清),Bixi XUE (薛碧曦),Lei GAO (高磊),Chenrui CHAI (柴辰睿) and Zhiwei DONG (董志偉)
1 North China Electric Power University,Beijing 102206,People’s Republic of China
2 Institute of Applied Physics and Computational Mathematics,Beijing 100094,People’s Republic of China
Abstract In geostationary orbits and other quasi-vacuum environments,relativistic electron beams are affected by the initial emittance and space charge effects during the propagation process,resulting in beam quality degradation.Furthermore,axial energy distribution change in the beam and the axial transient electromagnetic effect caused by current changes in the head and tail regions of the beam also cause the beam to expand and affect its quality.In this study,the particle-in-cell method was used to construct a long-range propagation model of a relativistic electron beam in a vacuum environment.By calculating and simulating the axial energy distribution of the beam and the changes in the transient electromagnetic field,the axial effect during the propagation process was analyzed,and the parameter change law of the effective propagation of the beam was explored.This provided a theoretical reference for a more accurate assessment of the beam quality during propagation.
Keywords: relativistic electron beam,axial energy distribution,transient electromagnetic effect,particle simulation
1.Introduction
In the space environment,sounding rockets can emit highenergy electron beams and track the parameter changes in the process of long-distance propagation to trace the magnetic lines of the Earth’s magnetosphere,obtain space information from astrophysical research scientific data,and perform other functions [1-4].Therefore,the long-range propagation of charged particle beams has considerable significance in the field of space exploration.When a relativistic electron beam is emitted into a quasi-vacuum environment,under the influence of the initial emittance and the space charge effect,the beam will disperse in all directions [5,6].When a relativistic electron beam is emitted into the geomagnetic environment,in addition to dispersion,the magnetic fields in different directions will also cause changes and losses in the quality of the electron beam,including centroid deflection,shape change,and fluence rate distribution [7].However,these phenomena are merely some of the factors that affect the beam quality and effective propagation distance in vacuum and geomagnetic environments [8].Considering a beam with a limited axial length as an example,on observing the detailed internal physical process during propagation,it is found that the energy distribution of the beam changes owing to the axial interaction between particles.Moreover,the sudden change in current in the head and tail areas of the beam will also cause an axial transient electromagnetic effect,resulting in ‘head erosion’ and ‘tail erosion’ of the beam.The axial effects in these propagation processes also affect the beam focusing and reduce the beam quality.Therefore,to describe the long-range propagation process of relativistic electron beams in a vacuum environment meticulously,it is necessary to simulate and analyze the main characteristics and mechanisms of the axial effect.Based on the study of long-range propagation(kilometre range) of a relativistic electron beam in vacuum and geomagnetic environments [6,7],this study further examines the various effects inside the beam to better analyze the propagation process and lay a theoretical foundation for the application of electron beam long-range propagation in space exploration and other applications.
The head erosion effect caused by the gradient change of current during electron beam propagation has been reported theoretically and experimentally [9-12],however,these studies were mostly conducted in the 1980s.Sharp and Lampe modelled the head erosion effect of a relativistic electron beam in 1980,and evaluated and analyzed the beam erosion rate,current neutralization degree,and other parameters [10].However,the change in the energy distribution caused by the particle axial space charge effect and its influence on the propagation results were not considered.Bouchet et al presented the simulation results of short-range propagation of a 100 MeV and 10 kA electron beam in an atmospheric environment in 1988 [11].Werner et al carried out an experiment on relativistic electron beam propagation in a plasma channel in 1994,and calculated the total erosion rate of short-range propagation of a beam in a metal-enclosed environment [12].Although the above studies in the 1980s involved the head erosion effect,due to the limitations of simulation technology and experimental conditions at that time,the comprehensive effects of the transient electromagnetic effect and axial energy distribution were not studied,and the propagation distance was short.In recent years,with the rapid development of computer technology and experimental hardware equipment,many countries have diverted more attention to the development of high-power pulse technology,space physics,and other fields,and research in these fields has gradually restarted.Taking the vacuum environment as the propagation background,this paper establishes the long-range propagation model of a relativistic electron beam based on the particle-in-cell (PIC)method.The axial energy distribution of particles in the beam and the transient electromagnetic effect in the head and tail areas are simulated.Combining the theoretical analysis and simulation results,the comprehensive influence of each axial effect on the propagation results and the change of beam qualities are qualitatively analyzed,and the variation law of effective beam propagation parameters is further explored.
2.Axial effect analysis of relativistic electron beam propagation
A finite-length bundle,whose initial size is larger in the axial direction than in the radial direction,is transmitted in the xaxis direction and the axial effects in the process are analyzed.
2.1.Axial space charge effect
In the long-range propagation process over thousands of metres,the relativistic electron beam generates an axial electric field owing to the interaction between the internal particles.Its internal repulsive force decelerates the tail electrons via the forward electrons,and the head electrons accelerate,resulting in changes in the axial velocity and energy distribution of particles in the beam [13,14].The relationship between the electric field and charge distribution is given by equation(1),whereEis the self-generated electric field,ρis the charge density,and0εis the vacuum dielectric constant
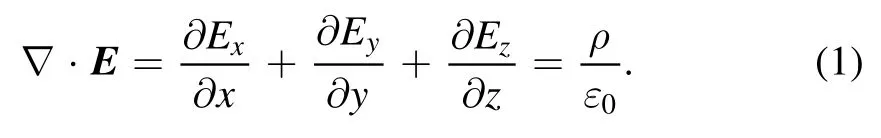
Figures 1(a)and(b)show the axial velocity distributions of the axial finite-length beam during and after launch,respectively.At the time of emission of the beam,the electrons at the tail are at the initial speed set by the emitter.However,the electrons at the head of the beam are accelerated by forward particles based on the initial speed,and the electrons at the middle and tail are decelerated,as shown in figure 1(a).After the beam is completely emitted,as shown in figure 1(b),there is a significant difference in the distribution of axial velocities of the particles at the head,middle,and tail of the beam.The velocity of particles at the head is greater than that of those in the middle (higher energy),whereas the velocity of particles at the tail is smaller (lower energy).Considering the axial velocity distribution and energy difference caused by the axial space charge effect,it can be seen that there is an additional‘pinch’driving force at the head of the beam as compared with the middle,and a stronger‘dispersion’ effect at the tail,which affects the shape of the beam in the propagation process.
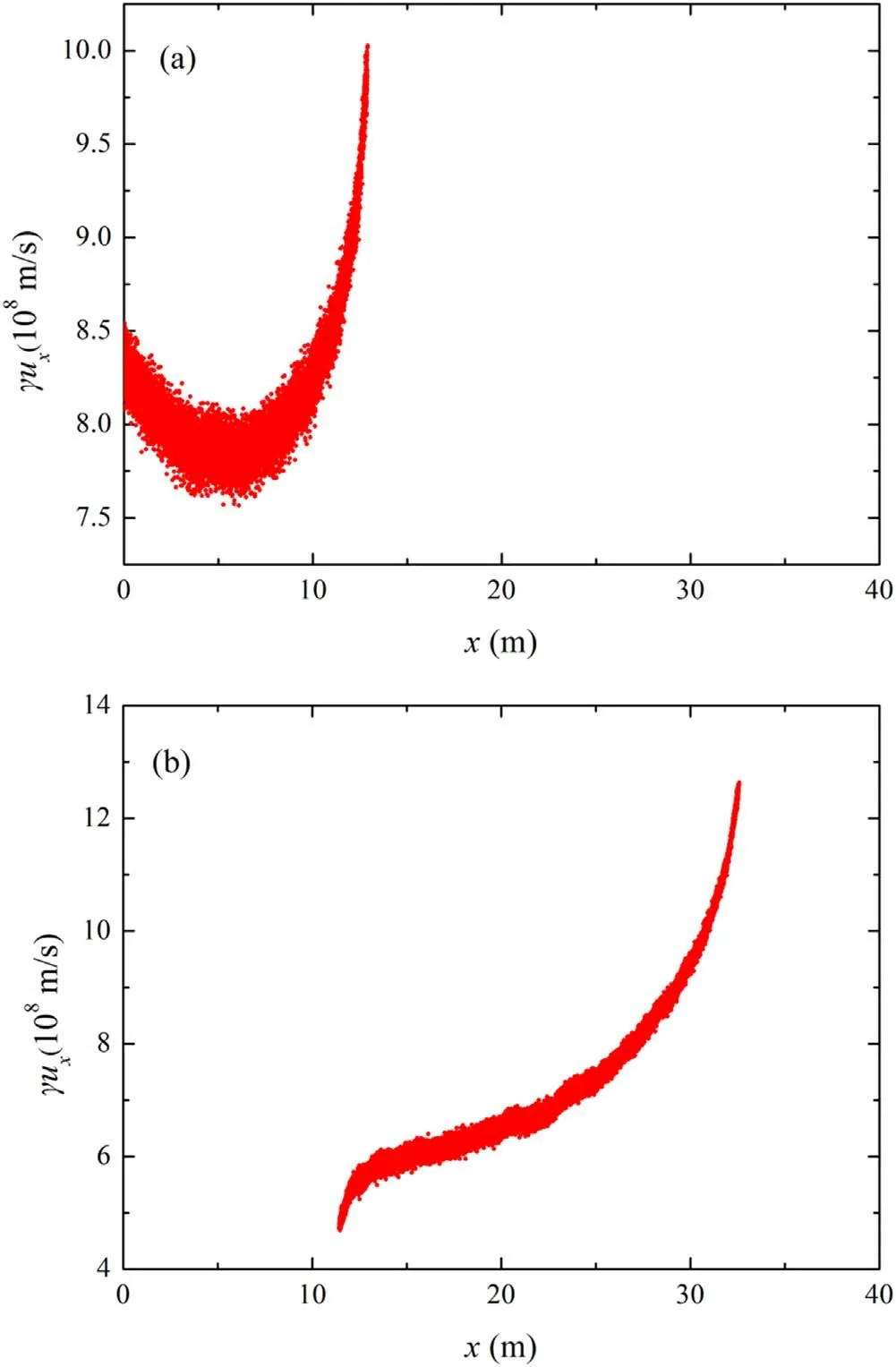
Figure 1.Distribution of the axial velocity of electrons (a) during launch,(b) after launch.
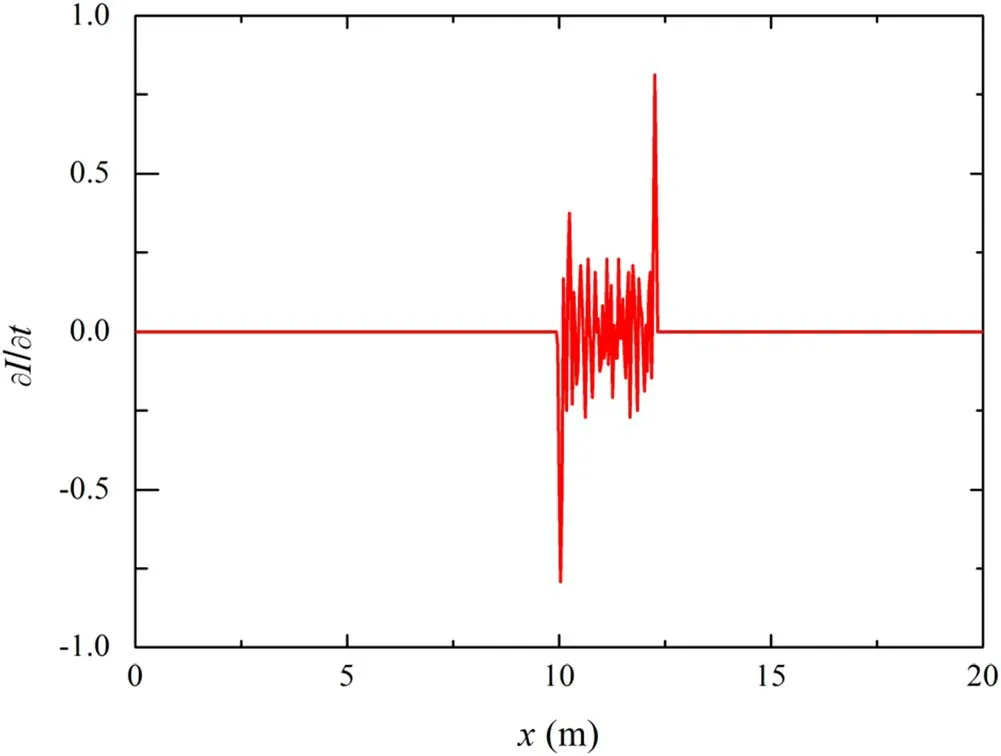
Figure 2.Normalized current derivative of the relativistic electron beam.
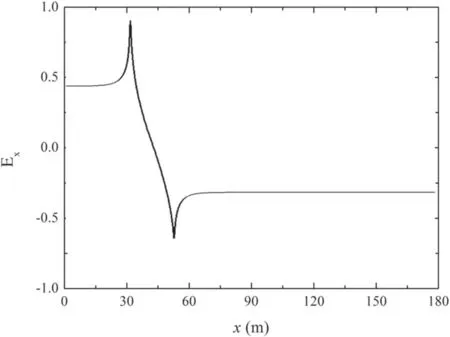
Figure 3.Distribution diagram of the time-varying induced electric field.
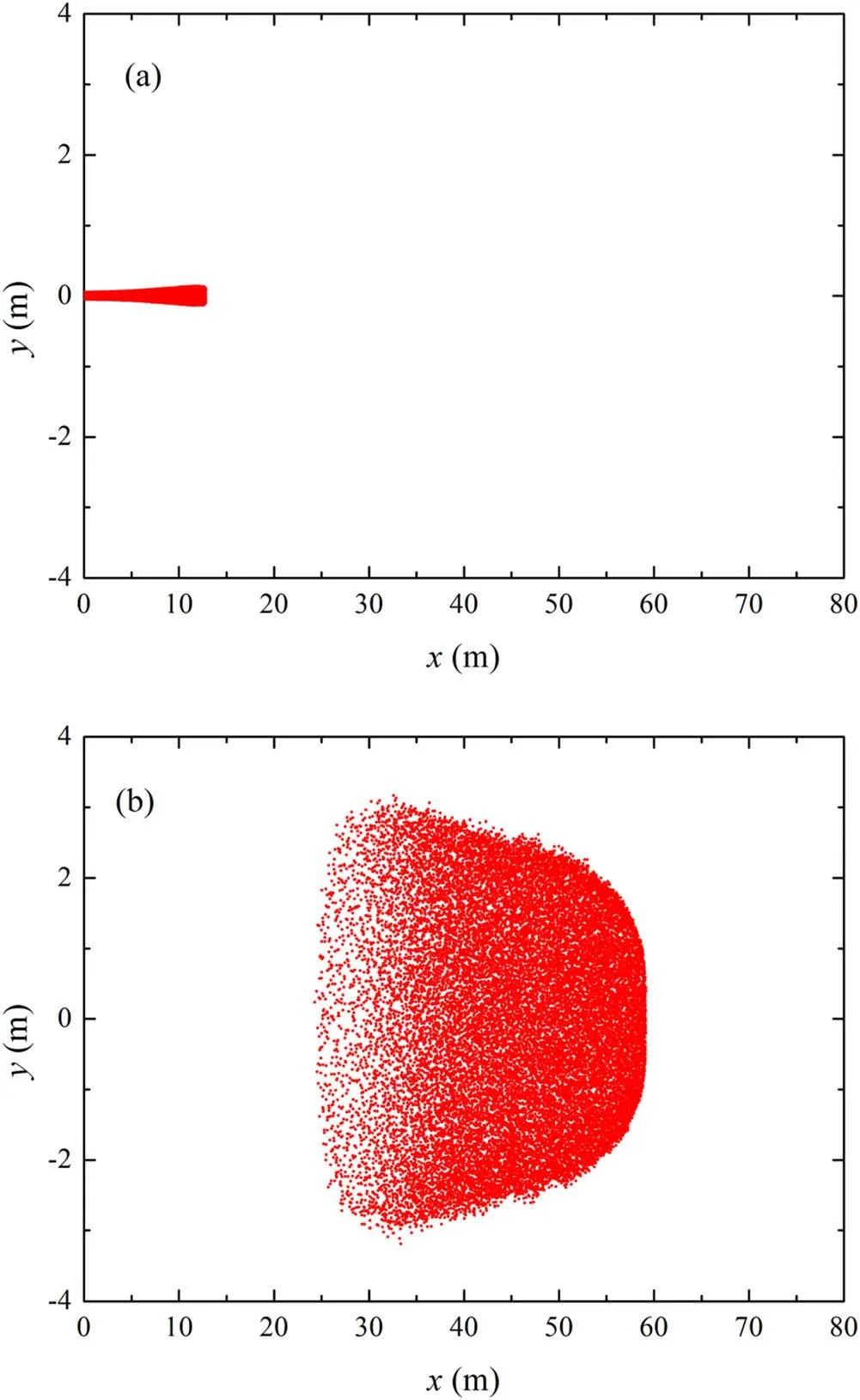
Figure 4.Dispersion of the relativistic electron beam (I0=100 A)(a) when not fully launched,(b) during propagation.
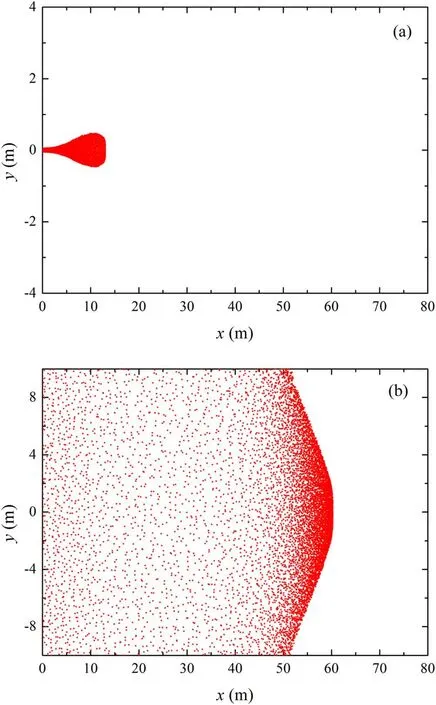
Figure 5.Dispersion of relativistic electron beam (I0=500 A) (a)when not fully launched,(b) during propagation.
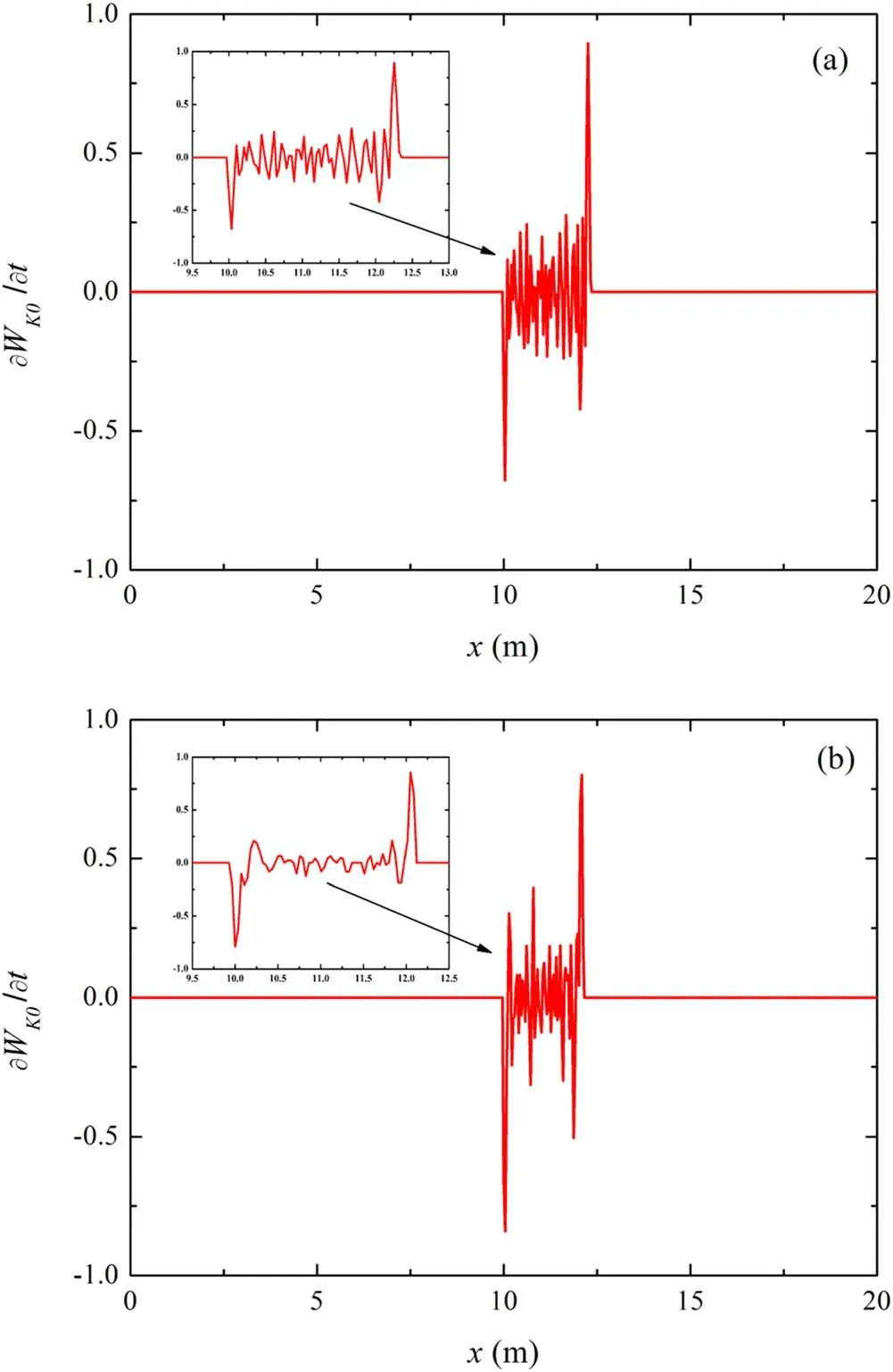
Figure 6.Normalized energy derivative of a relativistic electron beam with (a) WK0=1 MeV,(b) WK0=10 MeV.
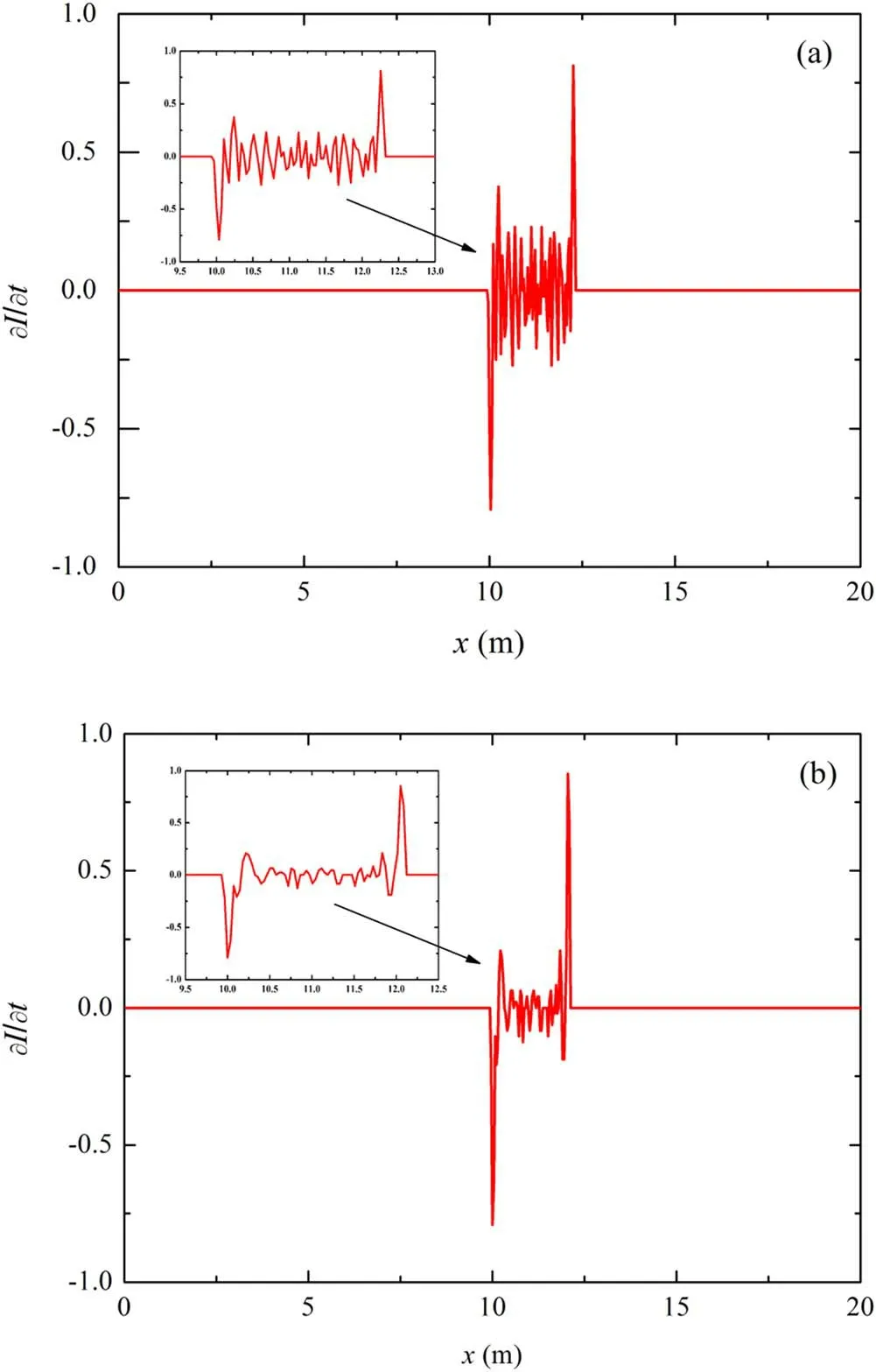
Figure 7.Normalized current derivative of a relativistic electron beam with (a) WK0=1 MeV,(b) WK0=10 MeV.
In a vacuum environment,the relativistic electron beam will disperse not only in the axial direction but also in all directions under the joint action of its own emittance and space charge effect during long-range propagation [15-17].However,when the axial size of the relativistic electron beam is much larger than the radial size (the initial energy divergence is small and negligible,and it causes negligible change to the emittance),the influence of the space charge effect on its propagation is mainly reflected in the radial dispersion.The influence of the radial dispersion has been analyzed in a previous study [6].Therefore,this study focused on the physical effects and physical images in the axial direction during beam propagation.
2.2.Transient electromagnetic effect
There was a sudden change in the current at the head and tail of the relativistic electron beam with a finite axial length.In this case,the current is a rapidly changing function of time,and the magnetic field and all current-based parameters are also functions of time.Therefore,there is a strong transient electromagnetic effect resulting in an axial time-varying electric field that tends to slow down the electrons.The space charge effect of the head and tail is usually stronger than that of the middle part.An additional dispersion drive will be generated on the basis of the radial expansion of the foundation,so that the electrons continue to disperse in the radial direction,resulting in erosion phenomena of the head and tail of the beam,namely the head erosion and tail erosion [18].
Based on the Biot-Savart law,when the current density of the electron beam is constant,the magnetic field generated when the current gradient changes at the head and tail regions is shown in equation (2),whereais the initial radial halfwidth of the beam,IBis the total current of the beam,andμ0is the vacuum permeability
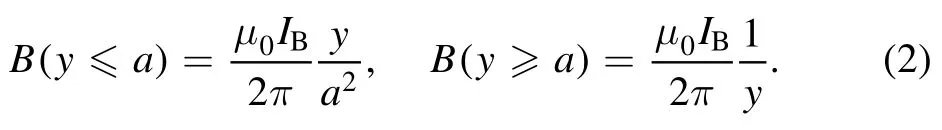
Using the Maxwell equations (equation (3)),the axial component of the induced time-varying electric field is obtained from equation (4).Here,L(y) is the self-induction coefficient varying with the electron position;τ(time within the pulse)is a function of time t,taking the beam head as the time starting point,that is,τ=t-z/βct.Compared with the middle part of the beam,the axial electric field is stronger because the current gradient at the head and tail is larger.The axial electric field causes the electrons to be dragged,resulting in a reduction in the energy of the electrons at the head and tail,which creates an additional ‘expansion’ driving effect on the beam.At the same time,the loss of electron energy and the radial expansion of the beam also affect the emittance of the beam,thus further enhancing the radial dispersion effect.Subsequently,the electrons at the head and tail of the beam move strongly in the radial direction,resulting in head erosion and tail erosion
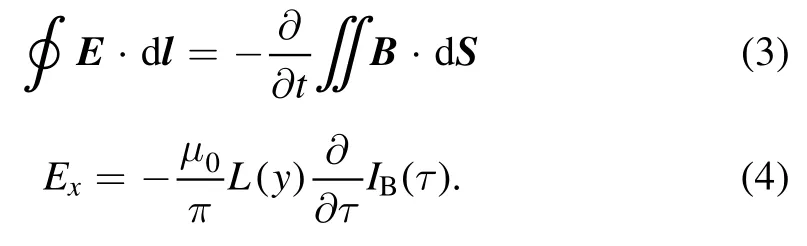
According to equation (4),the intensity of the transient electromagnetic effect changes with the current gradient.Therefore,it will also be affected by the beam shape.When the beam edge is flat along its length,rather than conical,these transient effects will be more intense owing to the larger current gradient change.Therefore,to observe the influence of this effect on the propagation process more clearly,the sheet beam model with a‘flat’head and tail is utilized for this research.
Using a sheet beam with finite axial length (Lx=2 m)for propagation simulation,and measuring the current of each axial cross section of the sheet beam at 10 m along the propagation path,the derivative of the current with respect to the propagation time is calculated.The normalization results are shown in figure 2.The change in the current gradient at the head and tail of the beam can be clearly observed and is symmetrical.Therefore,a transient electromagnetic effect caused by the sudden change in current in the propagation process exists and cannot be ignored.
2.3.Result analysis
Based on the above analysis,the axial space charge effect and transient electromagnetic effect will drive two opposite effects,of pinch and dispersion,at the head of the relativistic electron beam,which will counteract the radial expansion of the beam.At the tail of the beam,both effects will drive the dispersion effect to have a superposition effect on the radial expansion.To further study the mechanism and influence of the above two axial effects on the propagation process of the relativistic electron beam,a long-range propagation model of a relativistic electron beam is established using the PIC method to analyze the axial energy distribution of particles in the beam and the transient electromagnetic effect(both in the head and tail regions).
3.Propagation model and result analysis
3.1.Relativistic electron beam propagation model
PIC analysis is an important tool for studying the motion behaviour of charged particles.It can accurately simulate selfgenerated electromagnetic fields and related electromagnetic effects in the beam [19].To reduce the influence of electromagnetic oscillations and high-frequency electromagnetic noise,the PIC quasi-electromagnetic model was selected in this study.First,the self-generated electric field was calculated using the PIC electrostatic model.The numerical relationship between the self-generated electric field and the magnetic field is obtained from Maxwell’s equations,as shown in equation (5) (this equation holds for any charge density distribution) [10].Then,the self-generated magnetic field is added to the beam in the form of an applied field to perform iterative calculations to realize the comprehensive influence of the space charge effect in the propagation process[6,20-22].The electrostatic conditions were set at the left and right boundaries of the calculation window to weaken and absorb electromagnetic noise as much as possible without affecting the basic propagation process

At the same time,since the computing space including the actual effective beam motion in the long-range simulation process accounts for a small proportion of the total computing space required for simulation,computing resources and efficiency become the limiting factors,resulting in the difficulty of PIC simulation of long-range propagation.Therefore,a moving-window technology has been introduced to solve this problem.A calculation window with a reasonable size is selected to move with the particle beam and discretely divide the propagation area of the particle beam.It calculates and retains the propagation results of the particle beam,and realizes the long-range propagation simulation of the relativistic electron beam by connecting all the short-range propagation windows,thereby effectively improving the computing efficiency and saving computing resources and time [23].
3.2.Relativistic electron beam propagation results and analysis
The propagation simulation was conducted using a sheet relativistic electron beam with finite axial length(Lx=20 m),initial energy WK0=1 MeV,initial beam energy spreadΔW=0.01,and current intensity I0=100 A.The simulation takes a larger current intensity to obtain clearer propagation,because the transient electromagnetic effect increases with increasing beam current intensity,as observed from equation (4).
First,we detect the transient electromagnetic effect of the beam during propagation.Then we select the radial centre coordinate of the beam to create an axial profile line,and record the axial time-varying electric fieldExnormalization results of each position on the line in the moving window.As shown in figure 3,there is an obvious numerical mutation at the head and tail of the beam,owing to the strong transient electromagnetic effect in the head and tail regions because of the sudden current change in the propagation process.Since the axial field distribution is symmetrical in shape,we infer that the impact of this effect is the same at the head and tail.The value of the symmetry axis of the two peaks is slightly higher than zero.This is because the launcher in practical applications is a space suspension,and it does not take the charge elimination measures after emitting electrons; a positive electric field environment higher than zero will appear after emitting electrons.
We further analyzed the changes in the particle propagation process.The particle emission surface was placed on the left boundary of the initial calculation window (x=0 m).The state in which the beam was not completely emitted is shown in figure 4(a),and its internal axial velocity distribution is shown in figure 1(a).At this moment,the transient electromagnetic effect of particle emission should also exist,and the excessive dispersion of the beam head in the figure shows that its degree of influence is better than that of the axial space charge effect in this state.This is because under the combined influence of the dispersion trend of the transient electromagnetic effect and the pinch trend of the axial space charge effect,there is a yet more evident dispersion phenomenon at the beam head than that in the middle.When the beam is completely launched,the tail will also have a transient electromagnetic effect owing to a sudden current change.However,the axial velocity distribution caused by the axial space charge effect and transient electromagnetic effect will produce the same radial dispersion drive to the beam,so the shape of the beam changes and the evident dispersion appears at the tail,as shown in figure 4(b).It is observed that,since the two effects drive its dispersion at the end of the beam in a ‘superposition’ mode and at the head of the beam in an‘offset’ mode,the dispersion degree of the tail is significantly stronger than that of the head.The shape of the beam shows that the tail devours the head; in other words,the beam presents a‘side ladder’shape as a whole,and there is no erosion on the head.
In addition to the morphological analysis of the head and tail,an evident radial dispersion in the middle of the beam can also be observed in figure 4.As described in section 2.1,when a flaky beam with a long axial length is used for propagation research,a radial dispersion always exists at each part of the beam and affects the beam quality during the beam propagation.Therefore,although the axial space charge effect and transient electromagnetic effect have a negligible influence,the middle of the beam will have a non-negligible radial expansion owing to the radial electromagnetic field induced by the self-generated charge effect.Its expansion degree will be between the tail(the dispersion driven by the superposition of the two effects)and the head(the dispersion driven by the offset of the two effects),and the middle particles connect the head and tail particles,so that the beam appears as shown in figure 4(b).Thus,the dispersion degree is gradually enhanced from the beam head to the tail in the radial direction.
4.Analysis of the influence of beam parameters on the axial effect
As shown in section 2,the axial space charge effect and transient electromagnetic effect on the head and tail of the relativistic beams are both affected by the initial parameters of the beams during propagation.In this section,the effects of the initial current intensity and initial energy of the beam on each axial effect and the overall process during propagation are investigated.
4.1.Influence of current intensity on propagation effect
According to equations (1) and (4),the axial space charge effect and the transient electromagnetic effect at the head and tail of the beam are related to the initial current intensity.Therefore,we use the flaky relativistic electron beam(WK0=1 MeV) in section 2.2,increase the current intensity by a factor of five,taking I0=500 A,and keep other initial parameters the same to explore the influence of current intensity on the transmission process.
The left boundary of the calculation window was considered to be the particle emission surface.When the beams were not fully launched,a more evident dispersion was still observed in the head than in the middle,as shown in figure 5(a).However,in relation to figure 4(a),in figure 5(a)it can be observed that when the current intensity increases,the dispersion degree of the beam head with I0=500 A is significantly stronger than that with I0= 100 A.Subsequently,when the beams are fully launched and have propagated for a certain distance,the shape of the beam in figure 5(b)is similar to that in the case of low current intensity; the radial dispersion degree increases in the tail due to the superposition of the two effects.The dispersion degree of the head is much lower than that of the tail due to the offset of the two effects,while the middle of the beams is still connected with the head and tail.However,it can be observed from comparing figures 4(b)and 5(b) that the radial dispersion of the tail becomes more intense owing to the increase in the current intensity,resulting in some edge particles flying out of the calculation window because of the radial movement.
The propagation results for different current intensities show that the space charge effect and the transient electromagnetic effect of the relativistic beams increase with an increase in the current intensity,resulting in a larger radial dispersion degree of the beam.The results are in accordance with the theoretical formula; the two effects of the beam are positively correlated with the current intensity.
It is worth noting that,according to the above propagation process diagram,the relativistic beam will have very significant radial dispersion when the propagation distance is tens of metres,resulting in beam quality loss,and affecting the propagation process.This is owing to the strong transient electromagnetic effect at the head and tail of the beam at a high current intensity.Therefore,to observe the simulation results more clearly and shorten the simulation time,the simulation in this study adopted the limit case with a strong current intensity.However,when relativistic beam propagation is applied to the actual background,more reasonable beam parameters will be selected,and such a strong dispersion will not interfere with the propagation quality.
4.2.Influence of energy on propagation effect
In a space environment,relativistic beams of different energies are typically applied to different missions.Therefore,in this section,relativistic beams with initial energies of WK0=1 MeV and 10 MeV are considered,to explore the influence of the initial energy of the beam on the propagation process.
As mentioned in section 2.1,during the process of beam propagation,the axial electric field appears because of the space charge effect,which affects the energy and velocity distributions of the internal particles.In section 2.2,we measure the energy distribution of the internal particles of the beam at the propagation distance x=10 m,and calculate its derivative with respect to the propagation time.The results of the normalized energy derivative of the beam with initial energies of 1 MeV and 10 MeV are shown in figure 6.
The current detection was also set at the propagation distance of x=10 m to obtain the current changes at each axial section of the beam under the two initial energies and to calculate its derivative with time.The normalized results are shown in figure 7.
It can be seen from figures 6 and 7 that when propagated to the same distance with an increase in the initial energy,the energy derivatives of the particles in the relativistic beam and the current derivatives of the head and tail change slightly.This indicates that the initial energy of the beams has no influence on the axial space charge and transient electromagnetic effects.
According to section 2.1,the energy distribution in the beam will change due to the axial charge effect(which can be obtained from the change of axial velocity distribution of internal particles).It can be observed from figure 6 that the normalization results of the energy derivatives of beams with the same initial current intensity (I0=100 A) but different initial energies (WK0=1 MeV and 10 MeV) are the same.It can be observed that the degree of influence on the change in the internal energy distribution is the same as that on the increase in the initial energy.Moreover,it can be seen from equation (4) that the transient electromagnetic effect is directly proportional to the derivative of the current.The normalized results of the current derivatives of beams with the same initial current intensity(I0=100 A)but different initial energies (WK0=1 MeV and 10 MeV) are similar (figure 7);therefore,it is considered that the intensity of the transient electromagnetic effect is also the same.This indicates that the initial energy of the beams has no obvious influence on the axial space charge and transient electromagnetic effects.
The basic radial dispersion of the sheet beam can be described by the beam envelope equation shown in equation (6) [6,13,15],whereKx=Therefore,when the other parameters remain the same,the radial space charge effect decreases with the increase in the initial energy of the relativistic beam,and the radial dispersion is not evident.Moreover,the simulation results of studying the influence of beam energy on the basic radial dispersion show that the basic radial dispersion degrees of electron beams with WK0=1 MeV and WK0=10 MeV are quite different

Based on the above analysis,the initial energy has a negligible influence on the axial space charge effect and transient electromagnetic effect in the propagation process,but has a significant influence on the basic radial dispersion.Therefore,in the process of propagation,the space charge effect (both axial and radial) is the main factor affecting the beam shape and beam quality and has a stronger influence than the transient electromagnetic effect.
5.Conclusions
The influence of the axial effect on beam quality during the long-distance propagation of relativistic beams in a vacuum was studied by calculating and analyzing detailed physical processes,such as the transient electromagnetic effect and axial space charge effect.The simulation results show that along the beam axis there are energy distribution changes caused by the space charge effect,and transient electromagnetic effects caused by the current gradient change during propagation.The axial space charge effect provides the pinch drive at the head and dispersion drive at the tail.The transient electromagnetic effect provides a dispersion drive at both ends of the beam.Therefore,the above two effects have an offset effect on the dispersion at the head of the beam and have a superimposed influence at the tail.It can be observed from the shape diagram of the beam that the dispersion degree of the tail region of the beam is evidently stronger than that of the head region during propagation.
Further study of the parameters of the above two effects in the propagation process shows that both effects are enhanced with an increase in the initial current intensity of the beam.When the initial energy of the beam was increased,the influence of the two effects on the propagation did not change significantly,but the radial basic dispersion of the beam was significantly reduced.Therefore,it can be concluded that during the propagation process,the relativistic beam is comprehensively affected by the space charge effect (axial and radial)and transient electromagnetic effect.Among these,the space charge effect is the main factor affecting the beam shape and beam quality,and it has a greater influence than the transient electromagnetic effect.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Nos.61372050,U1730247) and the High-Power Microwave Key Laboratory Foundation Program(No.6142605200301).
 Plasma Science and Technology2022年6期
Plasma Science and Technology2022年6期
- Plasma Science and Technology的其它文章
- Recent progress on the J-TEXT three-wave polarimeter-interferometer
- Design of the stripping unit and the electromagnetic analysis unit for the E//B NPA on HL-2A/2M tokamak
- Space-resolved vacuum-ultraviolet spectroscopy for measuring impurity emission from divertor region of EAST tokamak
- Development of a combined interferometer using millimeter wave solid state source and a far infrared laser on ENN’s XuanLong-50(EXL-50)
- Bench test of interferometer measurement for the Keda Reconnection eXperiment device (KRX)
- Neutron yield measurement system of HL-2A tokamak
