Accurate prediction of the critical heat flux for pool boiling on the heater substrate
Fengxun Hai(海豐勛) Wei Zhu(祝薇) Xiaoyi Yang(楊曉奕) and Yuan Deng(鄧元)
1School of Energy and Power Engineering,Beihang University,Beijing 100083,China
2Research Institute for Frontier Science,Beihang University,Beijing 100083,China
3Beijing Advanced Innovation Center for Biomedical Engineering,Beihang University,Beijing 100083,China
4Hangzhou Innovation Institute,Beihang University,Hangzhou 310052,China
Keywords: boiling heat transfer,kandlikar model,critical heat flux,heater substrate
1. Introduction
Thermal management of high-power electronics requires cooling strategies capable of dissipating high heat flux while maintaining the device at low operating temperatures.[1,2]However,the heat transfer system is limited by the critical heat flux(CHF),at which the boiling process transitions from nucleate boiling to film boiling,causing an abrupt increase in the heater surface temperature. One of the most important aspects of avoiding burnout is how to predict the critical heat flux as precisely as possible.[3–5]
Over the last eight decades, the mechanisms that are responsible for the CHF have been the topic of extensive research and discussion.[6–8]Bubble interference,[9]hydrodynamic instability,[10]macrolayer dryout,[11]hot/dry spot,[12,13]and interfacial lift-off[14]are five potential mechanisms for accurately predicting pool boiling CHF that have been reported in the literatures. The hypothesis of hydrodynamic instability proposed by Zuber,[15]which is the first theoretical and mechanical CHF model, has received the most attention among the five mechanisms. Indeed, the majority of published pool boiling CHF research attempts to improve the Zuber model’s prediction capabilities by accounting for parametric variables that are not incorporated in the original model. Kandlikar[16]in particular presents a theoretical model based on force balancing that accounts for the near-field influence of wettability on the CHF of an upward-facing smooth inclined flat plate,as well as the far-field effect of hydrodynamic instability.
Thermal properties,[17,18]orientation,[19,20]heater size,[21]contact angle,[16]and surface roughness[22]all have an impact on CHF.Despite the fact that CHF is established as a hydrodynamic phenomenon,a lot of researches highlight the importance of surface properties. Several studies investigated heater thickness effects on CHF in pool boiling.[17,18,23]Nonhydrodynamic factors like the thermal properties and thickness of the heater have a major impact on the CHF of a surface.Several studies[17,24,25]investigated the influence of heater thickness and thermal properties of the heater material on CHF.To study the effect of the heater substrate thermal properties on CHF,Tachibanaet al.[25]experimentally determined the CHF on thin, vertically oriented ribbon heaters in water.The CHF was seen to be proportional to the heat capacity,which is the product of heater thickness, density, and specific heat of the heater. As can be anticipated,CHF increases asymptotically with increasing thickness in pool boiling,until it reaches a limiting value beyond which the increasing heater size does not play a role.Heater material is also regarded to be an essential factor affecting HTC and CHF.[26–28]Westwateret al.[26]established the CHF correlation,which indicated that a high thermal effusivity helps to transport heat away from the local dry area, delaying the occurrence of CHF. Grigorievet al.[28]investigated the heater material effect on the CHF by the experiments of liquid nitrogen boiling on different materials’surfaces and found that the CHF increased with the increase of thermal effusivity. However,the impact of the thermal properties of the heater material on determining the CHF over thick heater surfaces that are beyond the asymptotic thickness has not been fully explored.
In this paper, an analytical equation for the CHF of a heater substrate in terms of surface thermophysical characteristics is established. Pool boiling studies are carried out using distilled water to conduct pool boiling experiments on three different heater substrates(aluminum, brass, and copper). To establish the important characteristics that can best forecast CHF changes, the thermal conductivity of the tested material varies from 109 W/m·K to 398 W/m·K and the thermal mass(ρcp) ranges from 2.4×103kJ/m3·K to 3.4×103kJ/m3·K.Finally,Kandlikar’s CHF model is tweaked to account for the effect of the heater’s thermal properties on CHF. The anticipated CHF agrees well with the experiment and the literature,with a maximum inaccuracy of 5%.
2. Experimental procedure and setup
2.1. Pool boiling setup/measurement
Figure 1 shows the main pool boiling arrangement in detail. During the trials, the distilled (DI) water reservoir is kept at saturation temperature in the liquid chamber.[29]As shown in Fig.1(b),the test heater rod has the size of Φ10 mm(diameter)×20 mm (height) and is fixed spirally on a cartridge heater inside which is a 600 W silicon nitride ceramic heater. To guarantee minimal heat loss, the test rod is put inside a teflon enclosure and an air gap. The cartridge heater is wrapped by the thick glass wool to make sure of one dimensional heat conduction vertically. An electrical resistance auxiliary heater immersed in water in the liquid chamber serves as the heat source to maintain the saturation condition of DI water in the chamber. The liquid chamber has a side length of 150 mm, a thickness of 5 mm and a height of 200 mm and is directly open to the ambient atmosphere. Three thermocouples(TJ36-CASS-020U-6, OMEGA Engineering Inc.)are inserted half way into the 1 mm diameter drilled holes on one side of the test heater rod at 3 mm apart and are 0.4 mm from the top surface to measure the temperature distribution in the test heater rod. The signals from these thermocouples are received using OpreX data acquisition systems (GP 10) and the data from the acquisition systems is then transferred to the computer, recorded and analyzed using the UnivViewer program. The temperatures measured at specific points as shown in Fig.1(b)are used to calculate heat flux,wall superheat and heat transfer coefficient,which will determine the pool boiling efficiency.
The heat flux to the test surface is calculated based on one-dimensional heat transfer equation,[30]Fourier’s Law:

wherekCuis the thermal conductivity of copper, and dT/dxdenotes the temperature gradient along the heat flux, which is calculated using a three-point Taylor backward space series approximation from the thermocouples in the rod as follows:

whereTsatdenotes the saturated temperature of water inside the liquid chamber.
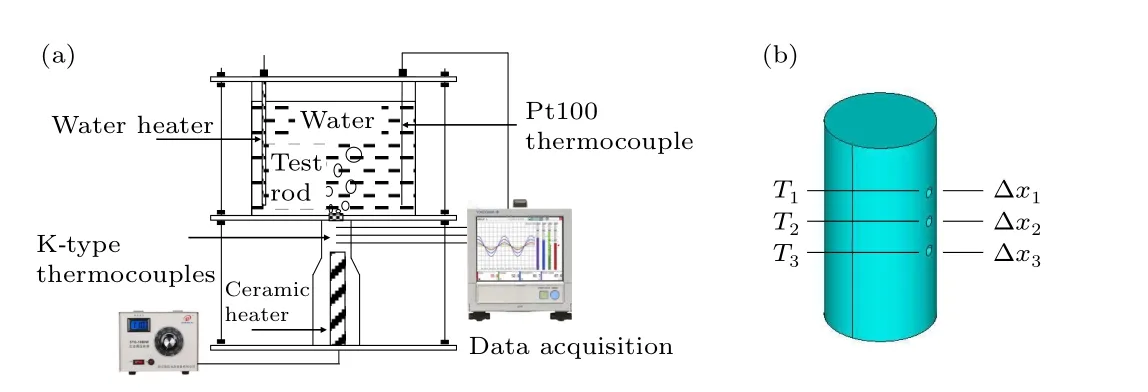
Fig. 1. (a) Schematic diagram of Pool boiling experimental setup; (b) the processed test sample rod which is screwed to the cartridge heater.
2.2. Uncertainty analysis
The main sources of uncertainty for the current setup were the bias and the precision errors. The bias error arises due to the calibration of the thermocouple, and the precision error is a result of the sensitivity of the measurement. For this study,uncertainty analysis is performed similar to that reported by Kandlikar and Patil.[31]The dimensional error due to sintering shrinkage,the limitation of the laser accuracy,and the solder layer thickness are±0.01 mm;the temperature measurement uncertainty for the precise K-type thermocouples is±0.2 K; and the power input uncertainty is±1 W. The error propagation analysis revealed that the uncertainty of the observed heat transfer coefficient at CHF is about 7.8%,and the uncertainty of the heat flux is 2.5%,which is within the range of the literature.[32]
3. Result and discussion
The three selected substrates are made of copper, brass,and aluminum. All samples are treated with 7000 mesh sandpaper, which is one-way scratched sequentially from 1000 mesh to 2000 mesh, 5000 mesh, and 7000 mesh as suggested.[33]To ensure repeatability, all samples are tested for three times.
Table 1 shows the thermal properties of the substrates tested.Each of the test heater rods is 20-mm high,and made of copper,brass,and aluminum,to guarantee that the CHF corresponding to each heater tested is independent of heater thickness.The microgeometry of a surface is one characteristic that is known to play a role in defining the CHF of a surface.[34,35]The test surface is cleaned with sandpaper to remove artifacts of the machining process such as burrs,pits,and grooves,ensuring that the microgeometry of the surface did not change amongst the multiple substrates examined. In order to ensure that the microgeometry of the surface does not vary between the different substrates tested,the surface roughness of all the substrates is maintained close to 0.05 μm(±0.01 μm)which represented the average arithmetic surface height(Ra).[36]The roughness range is low enough that no observable variation in CHF can be seen as a result of surface features. The thermal characteristics of the various substrates are summarized,as well as their contact angles,are shown in Table 1.

Table 1. Thermal properties of the substrates tested.
After polishing with 7000-mesh ultra-fine sandpaper,the contact angles of the three substrates, copper, brass, and aluminum, are shown in Fig.2. The contact angles of plain surfaces are all around 71°, which eliminates the impact of the surface on CHF performance. The bubble departure diameter is a critical parameter which governs the lateral coalescence of bubbles and the enhancement of capillary feeding of liquid.[37]According to the Fritz equation[38]
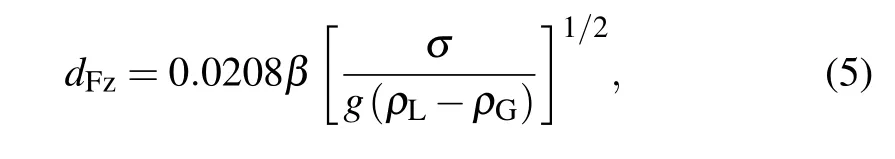
whereβis the static contact angle in degree,σis the surface tension force,gis the gravitational force,andρLandρGare the liquid and vapor densities,respectively. The calculated departure bubble diameter of three tested surfaces(brass,aluminum and copper) are 4.04 mm, 4.09 mm, and 4.04 mm, which is not much different.

Fig.2. Contact angles of plain surfaces of brass,aluminum,and copper.
The boiling heat transfer test apparatus is used to investigate and assess the performance of the three heat transfer substrates. Figure 3 shows the boiling curves of the three plain surfaces. As shown in Fig. 3(a), the CHF for aluminum is enhanced to 78.1 W/cm2, which is approximately 1.56 times higher than that of the plain brass surface (50.1 W/cm2).Moreover, the CHF for copper is 87.6 W/cm2, which is approximately 1.75 times higher than that of the brass surface.As can be observed, the CHF varies depending on the heat transfer material, and the higher the heat conductivity, the higher the CHF value. Therefore a model is developed to calculate the impact of the physical properties of the material on the CHF.
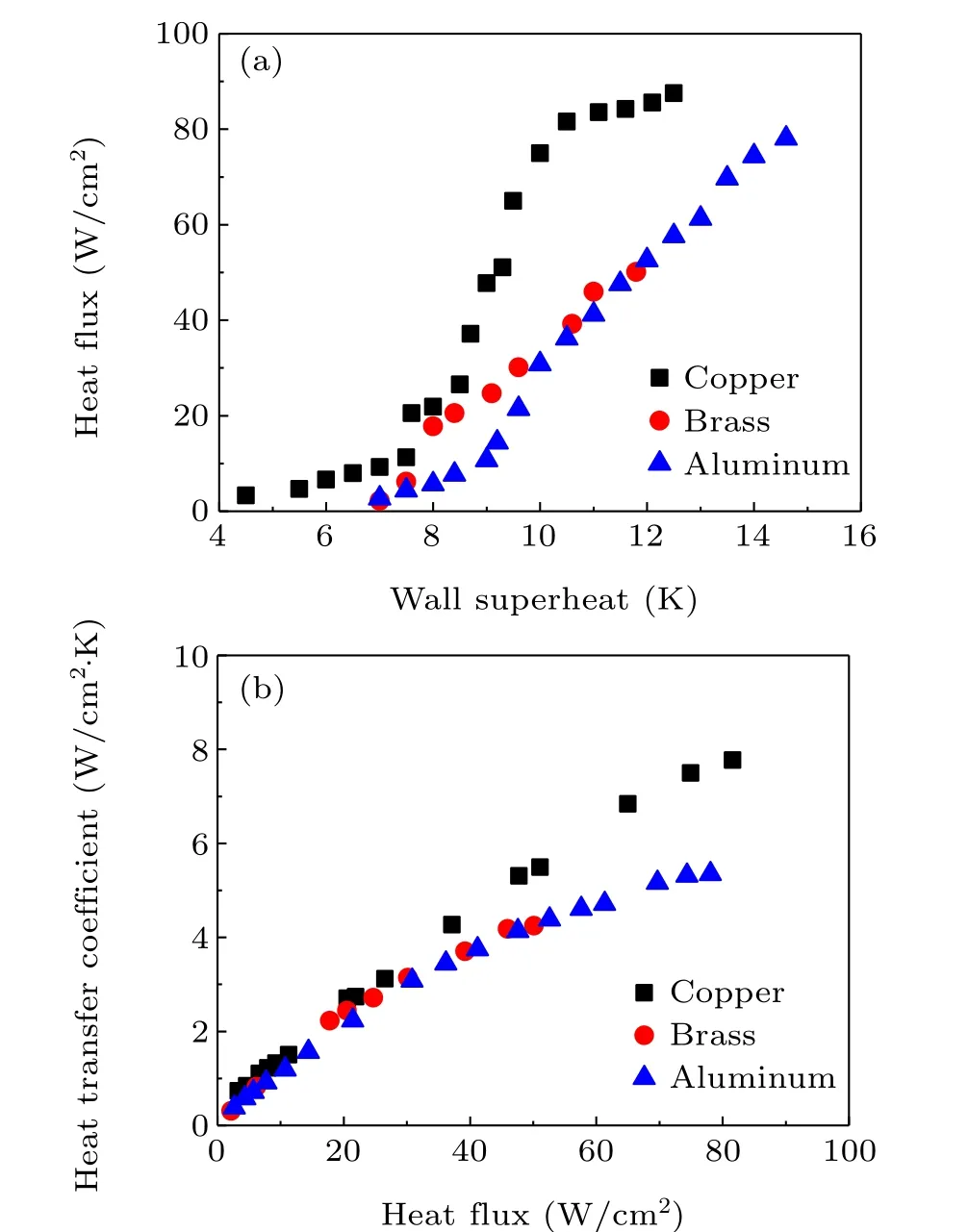
Fig. 3. (a) Pool boiling curves for the tested surfaces with water at atmospheric pressure. (b)Heat transfer coefficient comparison for the tested surfaces.
The heat transfer coefficient for the tested surfaces is shown in Fig. 3(b). When the critical heat flux on the plain copper surface is 87.6 W/cm2, the heat transfer coefficient is 7.8 W/cm2·K.The results reveal that surface materials have a substantial impact on CHF and HTC,with copper having the highest heat transfer coefficient and brass having the lowest one. At low heat flux, the difference is negligible, whereas at high heat flux, copper outperforms aluminum by 47% and brass by 85%.
This variation in CHF is attributed to the heater surface’s material properties, and further research in this study aims to improve the accuracy of CHF prediction by factoring in the impacts of heater material features. By considering the formation of steam jets above the nucleated bubbles and the liquid flow between the jets towards the heating surface,Kutateladze[39–41]proposed that the meaning of bubble generation and departure were lost near the critical heat flux condition,and critical condition is reached when the velocity in the vapor phase reaches a critical value. Following a dimensional analysis,he proposed the following correlation:
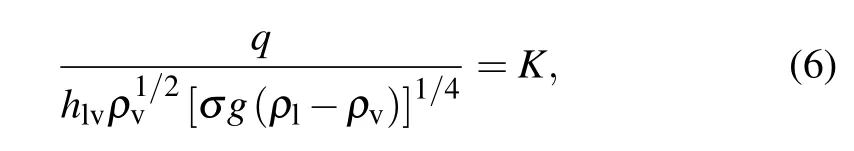
whereρvis the density of bubbles,hlvis the gas–liquid heat transfer coefficient, andρlis the density of the liquid. The value ofKwas found to be 0.16 from the experimental data.Zuber[15]further formalized the concept of hydraulic instability and proposed a value ofK=0.131. According to this,the critical heat fluxqof an ideal smooth surface is about 110 W/cm2.
Kandlikar[16]proposed the Kandlikar model for predicting CHF while considering the impact of thermal performance. This model was modified by adding a dimensionless correction factor to Zuber’s model,and the corresponding equations were given as
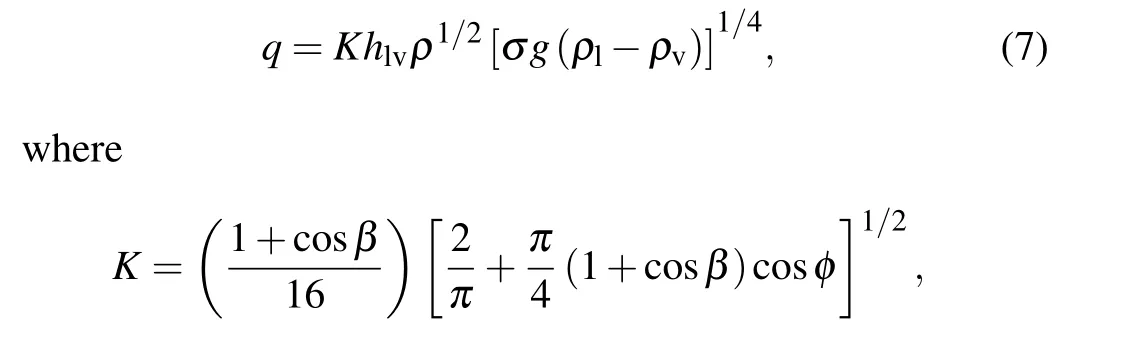
βis the contact angle of the heat transfer surface, andφis the angle between the heat transfer surface and the horizontal plane. In general,for a heat transfer surface inclined at an anglef,it is 0°when horizontal and 90°when it is perpendicular to the surface.
The model is based on boiling heat transfer data received from heat transfer materials under various metals, with the contact angle data being replaced in the computation, aKvalue of about 0.107 is obtained. The CHF of each surface may now be calculated independently and normalized using the Kandlikar formula,i.e.CHFexperimental/CHFKandlikarmodel.Thermal mass is the product of specific heat and density,represented as a given substance must absorb per unit volume of heat when the temperature rises by one degree.
The specific data are listed in the following table.

Table 2. Boiling heat transfer data under different tested materials.


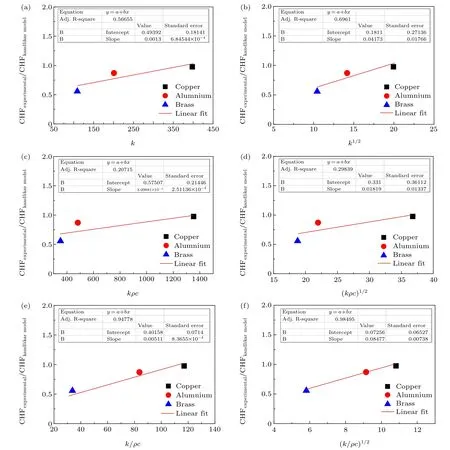
Fig.4. The analyze of k,k/ρcp,kρcp,,and the normalized CHF value.

or
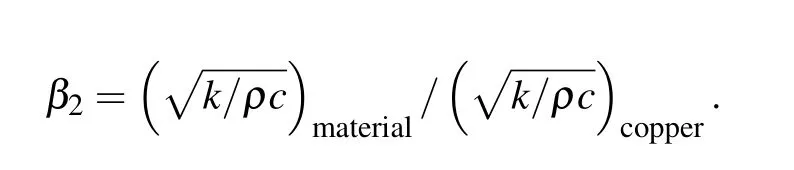
A comparison between the experimentally obtained CHF and the CHF predicted using the equation is shown in Fig.5.The substrate material consists of three different heat transfer materials: brass,aluminum and copper with the calculated CHF of copper as the reference material value.
Figure 5(a) shows a comparison between the experiment and the prediction calculated usingβ1as the correction factor. The solid line indicates the value when CHFpredicted/CHFexperimental=1,and the dotted line represents the difference between the experimental and predicted CHF values. The dotted line for brass is at-50%,indicating a 50%difference between predicted and experimental CHF values,with a high inaccuracy that makes further forecasts unfeasible.Figure 5(b)shows the comparison diagram of the experiment and the prediction generated with a correction factor ofβ2.All materials’CHF are properly predicted by the improved model,with an error of less than 5%. It can be observed that the predicted values are quite accurate for materials with highk/ρcp,such as copper, and the ratio essentially falls on the center of the solid line. The correction factor of high linear correlation considerably boosts the forecast for materials with lowk/ρcp.Therefore,the correction factor is chosen to beβ2.
The Kandlikar model is further revised after considering the thermal properties of the heater material,based on the above-mentioned experimental simulation verification:



Fig. 5. Experimental versus predicted CHF; (a) a comparison between the experimental and the predicted CHF using β1 as the correction factor; (b)a comparison between the experimental and the predicted CHF using β2 as the correction factor.
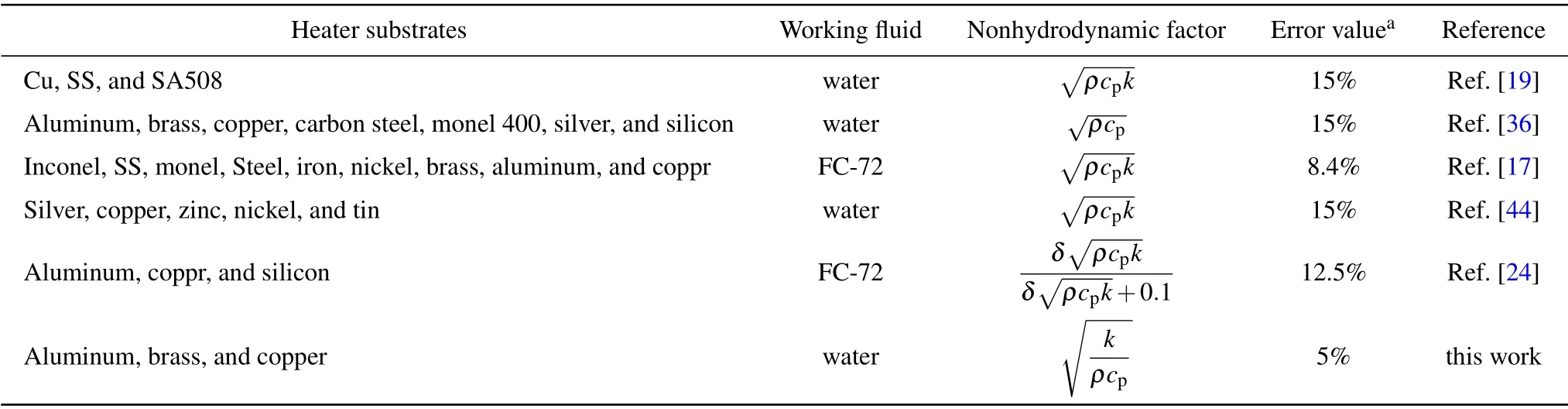
Table 3. Comparison of heater substrates and error value in saturated pool boiling in literature.
4. Conclusion



Acknowledgments
Project supported by the National Key Research and Development Program of China(Grant No.2018YFA0702100),the National Natural Science Foundation of China (Grant No. U21A2079), the Zhejiang Provincial Key Research and Development Program of China(Grant Nos.2021C05002 and 2021C01026), and the Fundamental Research Funds for the Central Universities.
- Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes