Voter model on adaptive networks
Jinming Du(杜金銘)
1Key Laboratory of Data Analytics and Optimization for Smart Industry(Northeastern University),Ministry of Education,Shenyang 110819,China
2Institute of Industrial and Systems Engineering,College of Information Science and Engineering,Northeastern University,Shenyang 110819,China
3Liaoning Engineering Laboratory of Operations Analytics and Optimization for Smart Industry,Northeastern University,Shenyang 110819,China
Keywords: statistical physics,opinion dynamics,evolutionary game theory,complex systems
1. Introduction
The models of statistical physics have been successfully used to understand complex systems and collective social phenomena,such as the emergence of cooperation,the formation of opinions, and the spread of information or diseases, motivated by the fact that statistical physics can describe how global complex properties arise from purely local rules.[1–4]Using the concepts of nonlinear dynamics, critical phenomena,and phase transitions,statistical physics attempts to grasp the basic characteristics of emergent social behavior by considering some simple rules.
Voter model[5,6]is an important and concise statistical physics model. It describes the evolution to consensus in a group of agents with discrete opinions. The voter model is similar to the kinetic Ising model with zero-temperature Glauber dynamics,[5]in which the individual (or spin) associated with a lattice sitercan have two different opinionsσr=±1. The dynamics of the system is realized by randomly selecting an individual and using the spin values of randomly selected neighbors. Through repeated updates, a finite and initially diverse group will reach a consensus over a period of time. In physics, some prominent properties of voter model have been studied,such as magnetization conservation. It is found that the study of voter model is helpful to understand a large class of nonequilibrium phenomena.[7]In particular, voter model produces nontrivial ordering phenomena through the iteration of simple rules. Because of this connection with nonequilibrium spin systems and its practical value in the study of interacting particles[5]and interactive systems,[6]voter models have been widely studied in physical literature[8–14]and beyond physics.[15]
The main reason why voter model has attracted extensive attention is that from the theoretical point of view of statistical physics, voter dynamics is one of the few stochastic many-body systems that are solvable in any dimension.Therefore, it can be used as a benchmark for the simulation or perturbation solution of more complex models. In addition, its properties are also helpful to understand other spin systems, such as Ising model and spin glasses.[1]Secondly,it has a wide range of interdisciplinary applications. Voter models and more complex variants of voter models, such as Axelrod’s model,[16]have been found to have many applications in the emergent phenomena of collective organizations in chemistry, population dynamics, evolutionary biology, and sociophysics.[1,14,17–22]Voter models, combined with other tools in statistical physics, such as mean-field-like methods and numerical simulations,[10–12,22–25]are widely used to describe the spread of culture,language or opinions in social systems.In particular,the voter model is perhaps the simplest and most completely solved of various models studying cooperative behavior.[8]
The voter model and its variants are mainly studied in the homogeneous and translationally invariant spatial structures, such as the regular lattices, in the research of classical physics. The regular lattice, however, can only provide a rough approximation of geographical proximity in sociophysics. Thus, people try to establish voter models on complex networks.[8–10,26]But so far,few studies take into account the fact that networks in real society have a dynamical nature,and the evolution of networks may affect the interactive process between nodes.[27–41]For example, the opinions of two individuals will determine whether they will establish a relationship. Hence,the opinion dynamics occur on an adaptively changing network. On the other hand, the network topology may affect the evolution of opinions. Therefore,the dynamics of adaptive networks include the formation of opinions and the evolution of network topology. The coupling between the two processes forms a coevolution of nodes and links. It reflects how people’s links affect their opinions and how their opinions determine their new links. It is of great significance to study the opinion dynamics on the evolving networks.[42–47]
The voter model represents the simplest model of opinion formation in the context of sociophysics, in which individuals can change their opinions according to the state of their neighbors. Accordingly, in the biological context, evolutionary game theory[48–52]provides a mathematical framework to study group behavior. It can be used to analyze the conflict of interest of rational individuals in the process of evolution over time. Moran process is a classic evolutionary process.[53–63]It represents a basic example of two species competing in the same environment,wherein individuals with higher fitness may be selected for reproduction. Although both models can describe the stochastic evolution of two-state individual sets,they have obvious differences, such as the order in which interacting individuals are selected. A selected node will copy the spin state of its neighbor in the voter model,however,individuals will transmit their state to adjacent nodes through reproduction and replace the corresponding neighbors in Moran process. The internal relationship between these two typical models in different fields is a topic worthy of in-depth exploration.
The main innovations and contributions of this paper are as follows. We propose a linking dynamics to model the voter model on the dynamically evolving network.This extension makes the classical statistical physical model traditionally studied on lattice and static networks more suitable for analyzing the spread of opinions in real complex networks. In particular,this novel model can be used to describe the coevolution of network topology and group decision-making. We theoretically analyze the voter model on the adaptive network and find some relationship between it and evolutionary game dynamics. With the help of these relations, we can study the statistical physical model on evolving networks from the perspective of game theory. This method makes it easy to interpret the decision-making on complex dynamic networks with classical game matrices. In this regard, we give some examples,including a case study of real data,to verify that the group behavior on dynamic networks can be predicted.
2. Formulation of the model
We consider networks possessingNnodes andLlinks.The voter model is defined as follows to characterize the dynamics of opinions. Each node in the network carries a spin,which is endowed with two states: spin up and spin down. If we use nodes to represent voters,a voterican choose between two different states (usually called opinions),σi=±1. The updating process of nodes in the network is as follows. Firstly,a node is randomly selected in the network. Then, the spin of the selected node is updated according to a simple majority voting rule. The probability that the selected node adopts a positive state +1 is proportional to the number of positive spins in its adjacent nodes,i.e. k+/(k++k-), wherek±represents the number of nodes with spin±1 in its neighbors,respectively. This means that if the number of positive spins connected to the focal node is more than that of negative,the probability of the selected node being positive at the next time is greater, regardless of its previous state. It is particularly noteworthy that in this updating rule, the future state of the node is independent of its initial state.
In the following,we propose a linking dynamics to study the evolution of network structure over time. Herein,the spins of nodes and the links between nodes coevolve. The existence of a link depends on the states of spins at both ends of the link,and the states of spins depend on the presence or not of links.Thus, we call the network adaptive. At each time step, with probabilityw, the state of spin updates as described above.Otherwise, the links in the network update. We denote that each link has a specified breaking probabilityk. Once a link is broken,a new one will be formed. We assume that the total number of links,L, remains constant during the evolution of links,which implies a limited resource environment.[47,64–66]
The linking dynamics is described as follows:
(I)A link is selected randomly from all the present ties.
(II)The selected link breaks off with probabilityk.
(III)If it breaks indeed,selecting one node occupying the two extremes of the broken link randomly. subsequently, the node randomly connects to another node who is not its current neighbor in the network.
There are three types of links in the network: ++,+-, and--. For the link of typeXY, whereXY ∈{++,+-,--}, it breaks off with probabilitykXY. Initially,each link is assigned a namei,wherei ∈{1,2...,L}.We specify a linki0randomly. Then linking dynamics happens. Ifi0is selected and breaks at the first time step,subsequently,another newly born link comes into being according to the linking dynamics we propose, denoted asi1. Otherwise, ifi0does not break,we denote thati1=i0. In analogy toi1,is,wheres >0,can be well-defined. In addition, we denote thatisis of typeT(is),whereT(is)∈{++,+-,--}(see Fig.1).
The linking dynamics is a Markov chain with state spaceS={++,+-,--}. We definex±as the fraction of spins with state±1 in the system. Ifx+x-k++k+-k--/= 0, the Markov chain is irreducible and aperiodic. Thus there exists a unique stationary distribution, which is determined by the normalized left eigenvector corresponding to the eigenvalue 1 of the transition matrix. The stationary distribution describes the percentage of time spent by the population in each homogeneous state in the long run. The stationary distribution of the link with typeXY(whereXY ∈S) is shown as follows:[47,51,67–69]

where ?Nis also the normalization factor.
3. Consensus probability
A basic property of the voter model is the consensus probability,which represents such a probability in a finite system:starting from an initial density of positive spin,x+,and finally reaching a consensus, for example, ending with all spins upward. In some contexts,this quantity is also called exit probability. We study voter models on adaptive networks. With probabilityw,the opinion updates,while,the linking dynamics occurs with probability 1-w. Ifw ?1,linking dynamics are much faster than opinion dynamics. Therefore,the nodes’states will not change until the linking dynamics reach the stationary regime. In other words, when considering the evolution of spin states of nodes, the link configuration of the network is in its stationary state. We focus on the evolution of the system under this assumption in this paper.
We define the number of spins with a positive state in the system asN+. Accordingly, the number of spins with a negative state isN-. Thus, the voter model on the adaptive network is a Markov chain with stateN+defined in the state space{0,1,...,N}. WhereinN+=0 andN+=Nare two absorbing states,representing that all spins are positive and all spins are negative,respectively. When all the nodes have reached a consensus, the system based on the voter model will remain unchanged. Therefore,the system described by state variableN+is a Markov chain with two absorbing states.
During the updating of the system, the stateN+is either increased by 1, decreased by 1, or unchanged at each time step. We takeN+increased by 1 as an example. At this time,we need to flip a spin whose original state is negative. First,a node in the system whose state is negative should be selected,and the probability is (N-N+)/N. Next, the selected spin flips. According to the definition in the model section, the probability of flipping a negative spin into positive is based on the majority voting rule,that is,the fraction of positive spins.Thus, the probability is:π--→-+/(π--→-++π--→--). Therefore, the probability that the number of spins with positive state in the system increases by 1 is[69]

4. Consensus time
In the voter model, the states (opinions) of the nodes stochastically change over time, so the system is evolving.When all the nodes are in the same state(consensus),the configuration is the absorbing state of the voter model. Therefore, the average time required for all the nodes in the system to reach a consensus is another basic property of the model.[7–9,70–72]We definet+jas the consensus time, that is,given that the system reaches the absorbing state with positive spins only,how long does this take when starting in statej?
Based on the exit probability obtained above,we start to derive the consensus time.

By using calculations similar to the previous iteration,we can get
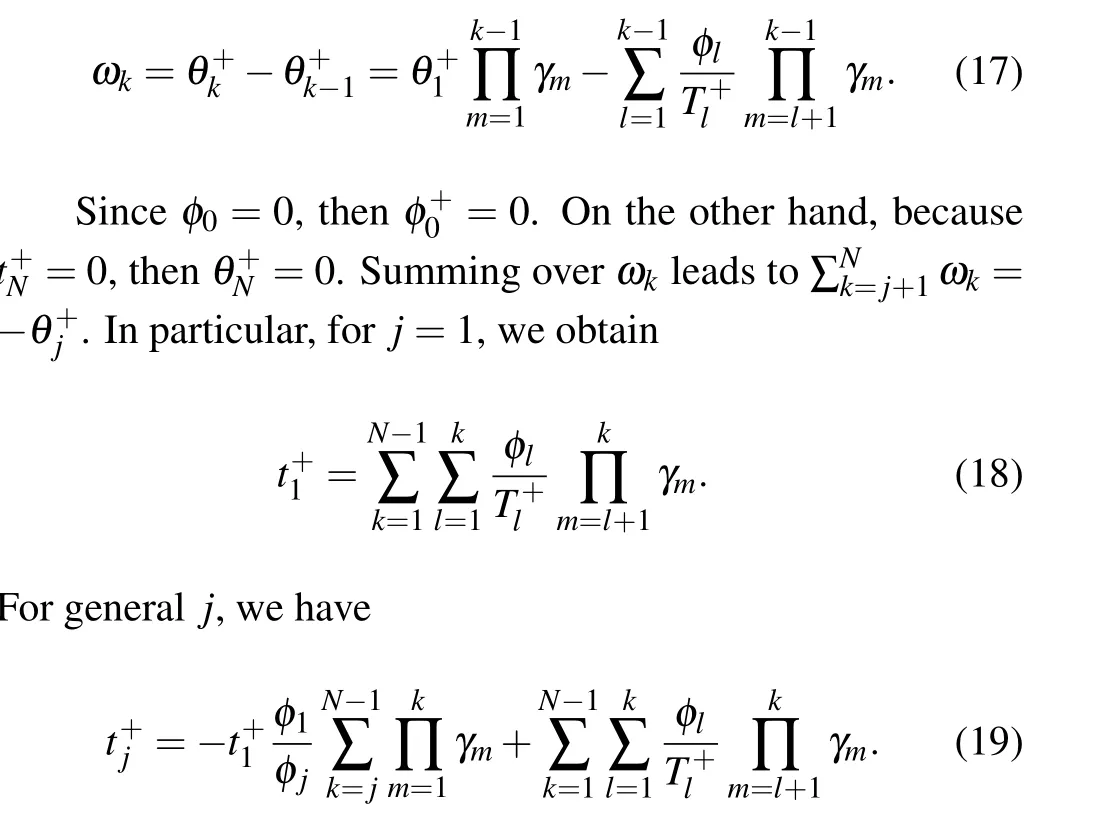
5. Evolution of opinions
For the evolutionary dynamics of opinions on the network,people are concerned about which opinion will become the mainstream in the society, or what will be the result of the spreading of opinions and the collision between different opinions? As a typical example of opinion dynamics, we are interested in the evolutionary trend of opinions in the voter model. In adaptive networks, the propagation of opinions is closely related to the change of network topology, which is the biggest difference from the system with static structure.In this section, we focus on the coevolution of networks and opinions,and explore the evolutionary trend of opinions.
5.1. Dynamics
We first consider a large-scale system. By considering a Kramers–Moyal expansion of the Master equation,[73,74]we have

When the population sizeN ?1,the probability density and transition probability can be expanded into Taylor series atxandt:

The above equation describes the deterministic time evolution of probability distribution,which has the form of the Fokker–Planck equation of the system.ForN →∞,the second term on the right of the equation approaches to 0.At this time,only the first term affects the dynamic process. Therefore, the change of the system state is reduced to the form of the following deterministic differential equation:

It can be seen that the dynamic process represented by the above formula can be characterized by the replicator equation,[51,75–77]which is a classical evolutionary model describing the strategy evolution in a very large and unstructured population. It governs the evolution of the densities of different strategies through a differential equation. In the replicator equation, the fraction of each strategy in the system is a function of payoffs, and the payoffs depend on the composition of the population, that is, the fractions of all the strategies in the population. Therefore,the dynamics is nonlinear in general.[52]
For the stochastic dynamics in finite populations,according to Eq.(13),the consensus probabilityφiof the voter model is determined byT-N+/T+N+. The transition probabilities can be obtained by Eqs.(3)and(4). Therefore,the consensus probability of the voter model on the evolving network can be shown as

Hence,it is found that the consensus probability and limiting behavior of voter model on adaptive networks can be characterized by evolutionary game dynamics. This points out that we can analyze the evolution of opinions on evolving networks from the perspective of evolutionary game.In fact,each item 1/kXYin the matrixMcan be understood as the expected duration time of different kinds of social linkXY. Such a matrix emerges from the voter model evolved on the adaptive network. With the help of such an emergent matrix,we will show how to study the evolution of opinions on adaptive networks.
5.2. Analysis
The evolution of adaptive networks depends on the connection and disconnection of different types of links. In the evolutionary process of opinions, the stability of social links has different situations. In the following,we discuss them respectively.
5.2.1. Like poles repel, unlike poles attract
The repulsion of the same magnetic pole and the attraction of different magnetic poles are common physical phenomena in nature. This phenomenon also widely exists in social groups,for example,heterosexual attraction. Such a situation is called out-group bias. This case describes that individuals are more inclined to establish connections with individuals holding different opinions. The practical significance of this case is as follows. As a classical opinion dynamics model, a very important application of voter model is to simulate the evolution of opinions in the election process. During a campaign, people try to persuade individuals with different opinions,convince them and change their opinion,so as to achieve the purpose of finally allowing them to join their own camp.Therefore, more interaction with people with different opinions is more meaningful to the diffusion of their own opinions.


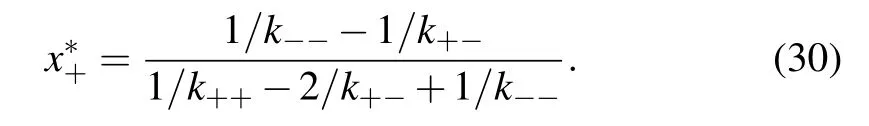
In Fig.2,the consensus probability for increasing initial fraction of positive spin in voter model on the adaptive network is shown. Here,k++=0.6,k--=0.6, andk+-=0.4. Thus the equilibrium of replicator equation isx*+= 0.5. At this time,the equilibrium point is a stable internal equilibrium. In other words,as long as different opinions exist at first,the system will eventually show a trend of coexistence of opinions,and the number of positive spins can be predicted through the equilibrium point. Different population sizesNare considered. WhenN →∞, the consensus probability is always 0.5,regardless of the initial value. The evolutionary process of the systems starting from different initial fraction of positive spins over time can be seen in Fig.3.

Fig.2. Consensus probability for the case k++>k+- and k-->k+-.

Fig.3. Evolution of opinions for the case k++>k+- and k-->k+-.
5.2.2. Like attracts like
The second case is the so-called in-group bias, which refers to the case that an individual is more willing to connect with an individual who has the same opinion as itself. This situation is also very common in real society. As the saying goes,“birds of a feather flock together.” For the adaptive network, this situation isk++<k+-andk--<k+-. How do the opinions evolve in this case? We will analyze it from the perspective of evolutionary game.

Fig.4. Consensus probability for the case k++<k+- and k--<k+-.


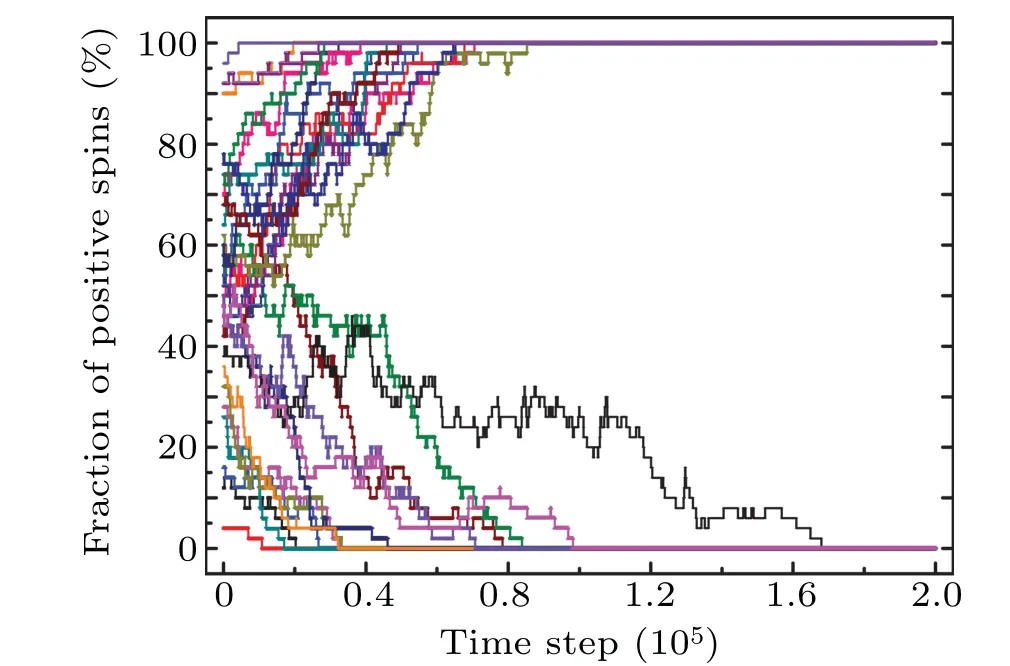
Fig.5. Evolution of opinions for the case k++<k+- and k--<k+-.
5.2.3. Biased preference

In Fig.6, the consensus probability for increasing initial fraction of positive spin in voter model on the adaptive network is shown. Ifk++=0.4,k+-=0.5, andk--=0.6, the positive state is the evolutionarily stable strategy. With the increase ofN, the consensus probability tends to 1. WhenN →∞, the consensus probability is always 1, regardless of the initial value.The evolutionary process of the systems starting from different initial fraction of positive spins over time is shown in Fig.7. It can be seen that the system will eventually be in a consensus state in which all spins are positive,as long as the number of initially positive spins is not too small.

Fig.6. Consensus probability for the case k++<k+-<k--.
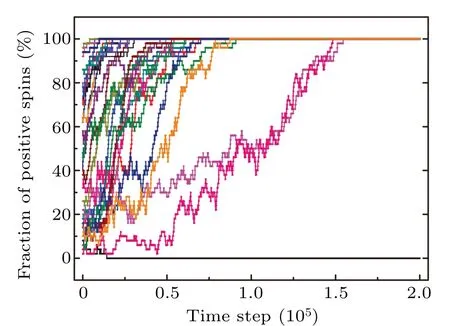
Fig.7. Evolution of opinions for the case k++<k+-<k--.
5.3. Discussion
Above,we have shown how to interpret voter model from the perspective of evolutionary game through some examples.In fact, it is worth mentioning that according to the relationship found in our previous analysis, the method of analyzing the fixation probability in the classic evolutionary game theory can be analogously used to analyze the consensus probability in the voter model. If both opinions are in-group bias, then both consensus states are stable Nash equilibria, as shown in Fig.4. The problem,then,is to figure out which opinion ultimately dominates the system. The existing theoretical results in evolutionary game theory will help us calculate the possibility of opinion+1 dominating the voting system.
Our results reveal the relationship between the voter model on adaptive networks and evolutionary dynamics. If the link breaking probabilities in the adaptive network are reduced to a minimum, the adaptive network degenerates to a static network. Obviously,the voter model on static networks(including complete graphs and regular lattices) can also be analyzed by Moran process and replicator equation. In addition, the replicator equation is differentiable homomorphism to the Lotka–Volterra equation,which is the well-known basic equations in ecology with interacting species.[51,85]Therefore,our results may also give some enlightenment on the connection between statistical physics model and ecological theory.
6. Case study
We further apply our method to a temporal network of contacts between students in a high school to show the ability to predict group selection. The data were collected in a high school of Lyc′ee Thiers, Marseilles, France in 2011 and 2012 using a proximity-sensing platform based on wearable sensors. The data is available on the webpage(http://www.sociopatterns.org/datasets/) and more details can be found in reference.[86]
The students involved in the study participate in a special project driven course. Students will first choose to join classes with different topics. We only consider two types of classes: academic and engineering. The former mainly focuses on theoretical knowledge such as mathematics,physics and chemistry. The latter focuses on engineering practice. All students must prepare a small project for presentation to obtain test results. In this process, several students can cooperate to complete a project according to their mastery of relevant knowledge and interest. Therefore,students may discuss problems or analyze data with other students in the same class or different classes through face-to-face communication. By interacting with different counterparts, students may change their interests in the process of learning. They can choose to adjust their classes in the next course selection.The data is collected through the measurement platform at contact times:it is based on wearable sensors embedded in unobtrusive wearable badges and detects whether the students wearing them are in close contact. The data collection infrastructure will generate a temporal network of contacts. Based on these data, we can analyze the contact patterns between students and classes,and further predict students’interest in class topics in the future.

Fig.8. The contacts matrices between students in each class. The matrices show the cumulative duration of contact between students in different classes in seconds throughout the study. Panel(a)shows the total duration of all contacts between individuals in the corresponding class. Panel(b)shows the average duration of contact between an individual and students in each class. In panel (c), each element of the matrix in panel (b) is normalized, and the average daily contact duration between each type of individual and students in each class is obtained in days.

Fig.9. Time evolution of the average cumulated time spent by a student in contact with other students during the study. The average time spent with students in the same class is shown in a blue triangle,and the average time spent with students in different classes is shown in an orange circle. It can be seen that the contact between classmates is significantly more than that between different classes,and this gap continues to widen with the accumulation of time. The inset is to more clearly show the contact time evolution between students in different classes.
We first count the number of individual contact events based on the data of 2011 and calculate the duration of various events (with the same class and different classes). Figure 8(a) shows the cumulative duration of contacts between students in different classes calculated throughout the study period. Figure 8(b)takes into account the different number of students in each class. In 2011,118 students(76 in the initial academic class and 42 in the engineering class)participate in the study. Figure 8(c)takes time into account because the data were collected within 4 days. The larger values observed on the diagonal of the matrix show that most contacts are students involved in the same class and very few contacts are observed between students of different classes, indicating that contacts have strong in-group bias in class(also shown in Fig.9).
According to the inverse relationship between breaking probability of links and contact duration time,we can roughly calculate the breaking probabilityk++=0.435 for classmates in academic class,k--=0.6025 for classmates in engineering class,andk+-=0.962 for students in different classes. Thus,according to Eq.(30),we can calculate a key equilibrium pointx*=0.33. Based on the analysis of in-group bias in the previous section,it is inferred that when the number of students in the academic class is greater than this value,students’choices will be greatly inclined to the academic class. Comparing the data of the two years,as shown in Fig.10,it can be seen that the proportion of students in the academic class did increase in the next year. Academic courses are becoming more and more popular,which is consistent with our prediction.In fact,as can be seen from Fig.9,with the learning process,i.e. system evolution, the contact between classmates increases significantly over time,while the contact between different classes does not increase obviously. This means that the breaking probability among students in the same class is decreasing day by day.Therefore,according to Eq.(30),x*is also decreasing,which reduces the threshold for the expansion of academic class.

Fig.10. The proportion of students in the two kinds of classes for the successive two years.
7. Conclusions
In this paper, we study the voter model on the adaptive network by proposing a linking dynamics.By theoretically analyzing the voter model on evolving networks, we found that the voter model on the adaptive network can be interpreted from the perspective of evolutionary game. Utilizing the theoretical results, we can predict the evolutionary trends of the system. The limitation of our work is that we separate the two dynamics of network topology evolution and opinion evolution,so as to facilitate theoretical analysis. Therefore,a novel theoretical framework that can better deal with this problem at similar time scales is a research direction of great theoretical value in the future. Besides,it is necessary to consider the cases of multiple opinions. The classical voter model of two magnetized states could be extended tonstates,which would be more beneficial to modeling the formation and evolution of opinions in real society.

Appendix A:Fixation probability of Moran processwhereN1andN2respectively represent the number of holders of the two strategies in the system. Obviously,N1+N2=N.
The Moran updating process is as follows. First, an individual is randomly selected in proportion to the individuals’fitness. This individual reproduces a same offspring. In order to keep the number of individuals in the population unchanged, a randomly selected individual is removed from the population before adding the offspring.
Thus, the system can be represented as a homogenous Markov chain with the number of individuals holding strategy 1 as the state (i). The state space is{0,1,2,...,N}. Obviously, there are two absorbing states in such an evolutionary system,that is,all the individuals adopt strategy 1(i=N)and all the individuals adopt strategy 2(i=0). We defineρkas the fixation probability, which represents the probability that the system starts withkindividuals holding strategy 1 and reaches the state of all strategy 1 (i.e.,i=N). Any stateiandjbelonging to the set{1,2,...,N-1}are transient, and stateiand statejare reachable to each other. Denotepi,jas the transition probability from stateitoj. If|i-j|>1,thenpi,j=0.Hence the transition matrix is tri-diagonal. For stochastic systems satisfying the above conditions, the fixation probability has the following form:[54,56,68,87]

Combining Eqs. (A1) and (A2), the fixation probability can be obtained as follows:

Comparing Eqs. (29) and (A8), it can be seen that the consensus probability of the voter model on the adaptive network is formally equivalent to the Moran game dynamics in the well-mixed population.
Acknowledgements
Project supported by the Major Program of the National Natural Science Foundation of China (Grant No. 71790614),the National Natural Science Foundation of China (Grant Nos. 61703082, 71520107004, and 71621061), the Fundamental Research Funds for the Central Universities, China(Grant No. N2004004), the General Program of the Educational Department of Liaoning Province, China (Grant No.LJKZ0013),and the 111 Project(Grant No.B16009).
- Chinese Physics B的其它文章
- Erratum to“Boundary layer flow and heat transfer of a Casson fluid past a symmetric porous wedge with surface heat flux”
- Erratum to“Accurate GW0 band gaps and their phonon-induced renormalization in solids”
- A novel method for identifying influential nodes in complex networks based on gravity model
- A novel car-following model by sharing cooperative information transmission delayed effect under V2X environment and its additional energy consumption
- GeSn(0.524 eV)single-junction thermophotovoltaic cells based on the device transport model
- Investigation of the structural and dynamic basis of kinesin dissociation from microtubule by atomistic molecular dynamics simulations

