Global Existence and Decay of Solution to Parabolic-Parabolic Keller-Segel Model in Rd
ZHONG Wenbin(鐘文彬), LIU Xiaofeng(劉曉風(fēng))
College of Science, Donghua University, Shanghai 201620, China
Abstract: We consider the global existence and decay of integral solutions to the parabolic-parabolic Keller-Segel system in d-dimension. On the one hand, by Banach fixed point theorem and some properties of heat kernel, we prove the local existence and the global existence of integral solutions for the different initial data under some conditions that involve the size of the initial data. On the other hand, in the case of global solutions, we obtain their optimal time decay by Gronwall’s lemma.
Key words: Keller-Segel system; global existence; integral solution; local existence; optimal time decay rate
Introduction
This paper is concerned with the following parabolic-parabolic Keller-Segel model
(1)
whereε>0,α≥0,u(x,t) represents the population of cells andv(x,t) is the density of a chemical substance,x∈Ω,t≥0.
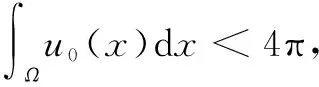
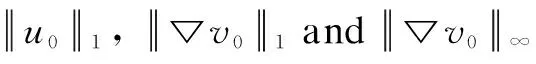
In this paper, we consider the solutions of the model(1) in the following integral sense:
u(t)=G(t)*u0-
(2)
v(t)=e-(α/ε)tG(ε-1t)*v0+
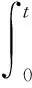
(3)
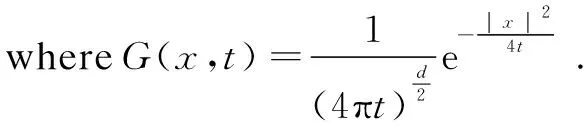
Firstly, we will show local existence to Eqs.(2) and (3), and have the following theorems.
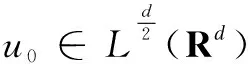
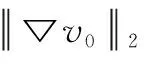
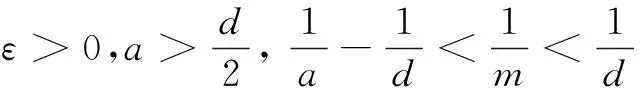
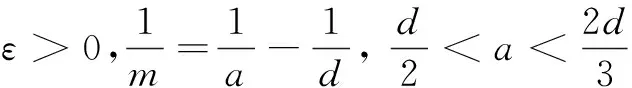
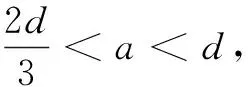
Secondly, we will show global existence to Eqs.(2) and(3), and have the following theorem.
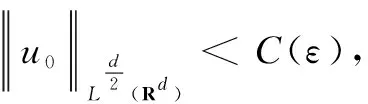
(4)
(5)
Finally, we obtain the optimal time decay rates of ▽uand Δv(t).
Corollary1The global integral solution (u,v) of the model (1) given by Theorem 4 satisfies
(6)
(7)
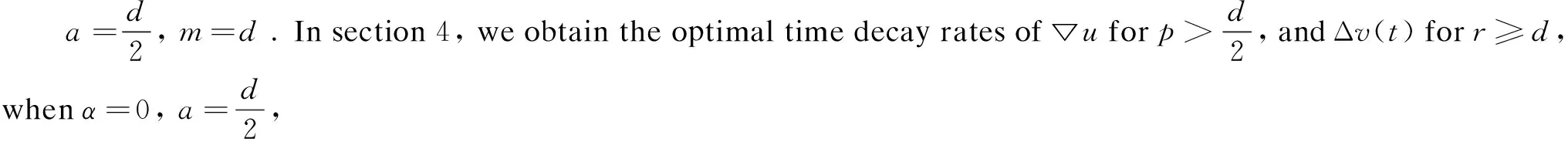
1 Preliminaries
Throughout this paper, we denote byLp(Rd), 1≤p≤∞, the usual Lebesgue space. We denote the beta function and the gamma function, respectively, which are

and

We denoteG(x,t) the heat kernel. The upper case letterCstands for constants depending onpand the initial data.
Gronwall’sLemmaLetT>0,A≥0,β∈(0,1] and letfbe a nonnegative function withf∈Lp(0,T) for somep>1 such thatp'max{α,β}<1. Then ifφ∈L∞(0,T) satisfies
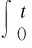
There existsC=C(T,α,β,p,fLp(0,T)) such that
φ(t)≤ACt-α.
For the proof, it has been proved in detail[18].
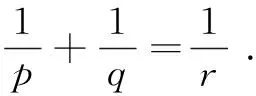
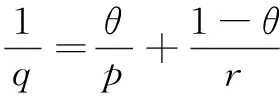
2 Local Existence
In this section, we will also make use of the following standard inequalities onG(t), for 1≤p≤∞,
(8)
(9)
ProofofTheorem1Forp∈(d,2d) is arbitrarily fixed,T>0,η>0 to be chosen later. Define
and
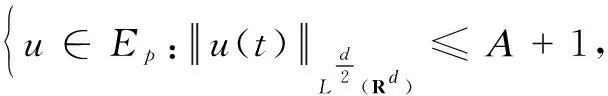
(10)
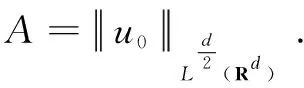
(11)
is a nonempty complete metric space.
Then, foru0andv0given as in the statement of the theorem and a fixedu∈Xp, we defineF:(Xp,dp)→(Xp,dp) and
F(u)(t):=
(12)
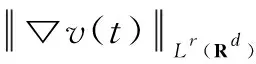

(13)
Then, using the inequality(13) forr=∞, we obtain
(14)
Therefore, by formulas (8)-(10) and H?lder’s inequality,
(15)
provided
(16)
(17)
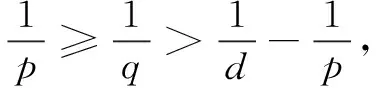

(18)
provided
(19)
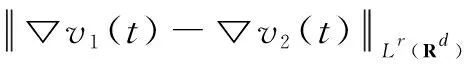
(20)
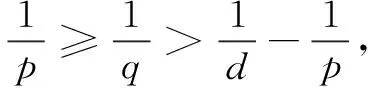
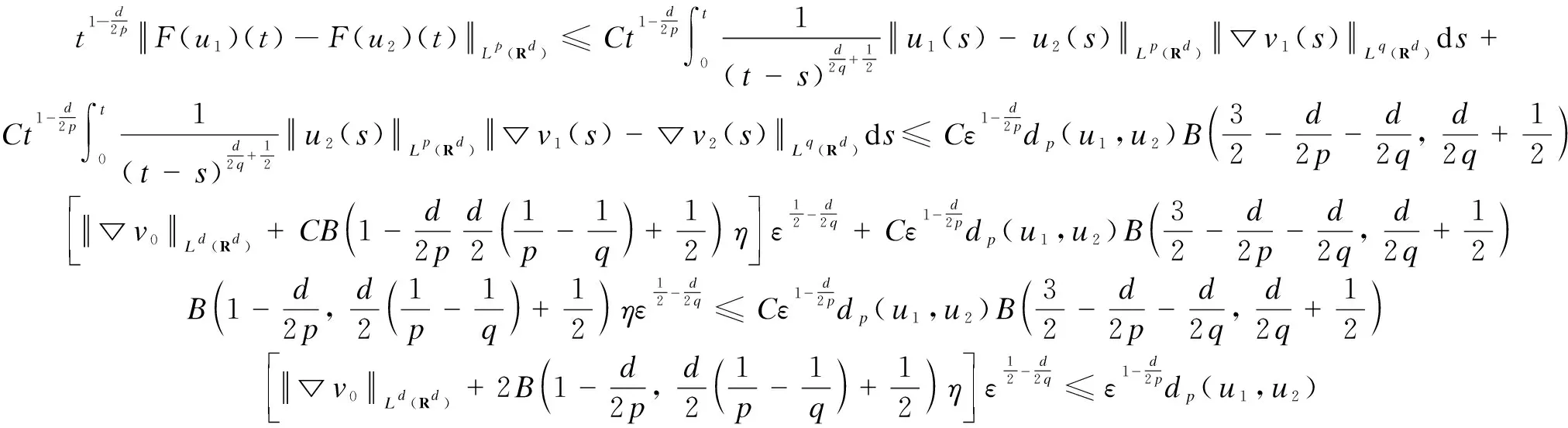
(21)
provided
(22)
To conclude, on the one hand, from the inequalities(16),(19) and(22), we can findδ>0 andη>0 such that if ▽v0Ld(Rd)<δ, inequalities(15),(18) and(21) are true. On the other hand, there existT>0 such that the inequality(17) is satisfied fort∈[0,T]. That meansF:(Xp,dp)→(Xp,dp) is a strict contraction andFhas a unique fixed pointuinXp. Then the local existence of Eqs.(2) and(3) is obtained by the Banach fixed point theorem.
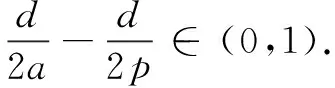
and
(23)
(24)
is a nonempty complete metric space.
Then, foru0andv0given as in the statement of the theorem and a fixedu∈Yp, we definevandF(u) by Eqs.(3) and(12) separately. Firstly, whenr≥p,r≥m, from the formulas (8),(9) and H?lder’s inequality, we have
(25)
(26)
From the formulas(8),(9),(23),(26) and H?lder’s inequality, we have
(27)
In the same way, forrit is defined as before andr>m>d, by the formulas(8),(9),(23),(26) and H?lder’s inequality,
(28)
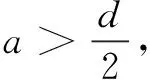
(29)
where it has been used that
(30)
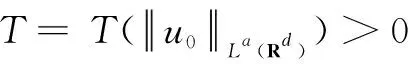

Then, foru0andv0given as in the statement of the theorem and a fixedu∈Yp, we definevandF(u) by Eqs.(3) and(12) separately.
Firstly, whenr≥p>m, from the formulas(8),(9) and H?lder’s inequality, we have
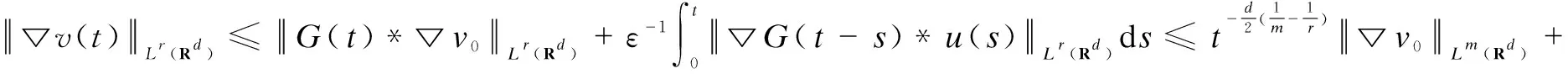
(31)
And using the inequality(31) forr=∞, we obtain
(32)
Therefore, by the formulas(8),(9),(23),(32) and H?lder’s inequality,
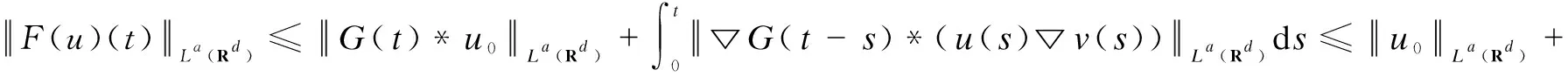
(33)
(34)
(35)

3 Global Existence
In this section, we will prove the theorem in two steps.
ProofofTheorem4First step: regularizing effects. Whenp,η, andTare chosen as Theorem 1, letq∈(p,∞).
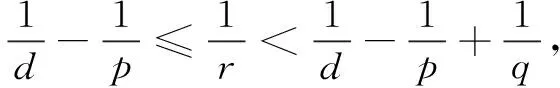
So whenq∈(p,∞), the inequality (4) is true.
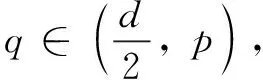
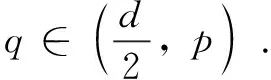
Letq=∞, since
u(2t)=G(t)*u(t)-
then by taking theL∞ofu(2t), from the formulas (8)-(10),(14) and H?lder’s inequality, we have for any 2t∈(0,T),
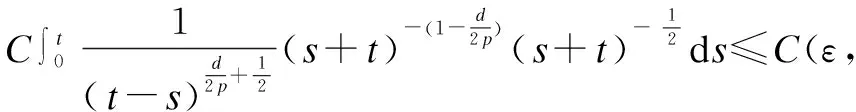
So whenq=∞, the inequality(4) is also true.
Whenr∈[p,∞], the inequality(5) can be obtained directly from the inequalities (13) and(14).
Whenr∈[d,p), from the inequalities (8)-(10) and H?lder’s inequality,
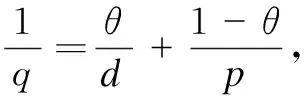
So, the inequality(5) is established up to now forr∈[d,p).

On the other hand, by considering the increasing behavior offp(t), it holds
where
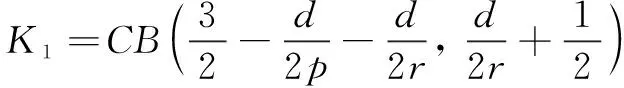
(36)
(37)
Then, from the inequalities (36) and(37), we have
(38)
Therefore, the global existence of Eqs.(2) and(3) follows when the condition (38) holds.
4 Time Decay Estimates of ▽u and Δv
In this section, we will make use of the variant below of Gronwall’s lemma and the inequalities (4) and (5).
ProofofCorollary1First of all, let us define(uλ,vλ),
uλ(x,t)=λ2u(λx,λ2t),vλ(x,t)=v(λx,λ2t),
whereλ>0. Obviously, whenα=0, if (u,v) is the global solution of the model (1), so is (uλ,vλ). And we have
(39)
and
(40)
Letp>d,t>0,τ>0, we have
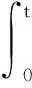
(41)
and
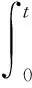
(42)
Moreover, by taking theL∞norm of the identity (41) and using the inequality (40) forr=∞, inequality (9) and H?lder’s inequality, we obtain
(43)
Taking theLpnorm of the identity(42), and by the formulas (9), (39), (40) and H?lder’s inequality again,
(44)
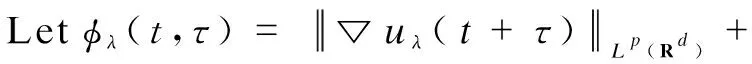
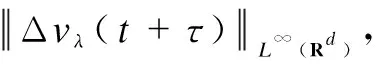
(45)
Whent∈(0,T],T>0, by Gronwall Lemma and the inequality(45),
(46)
Letτ=T=t=1, by the identity(46),
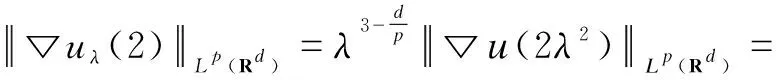
So whenp>d,r=∞, the inequalities(6) and(7) are also true.
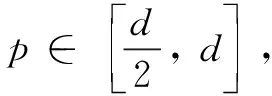
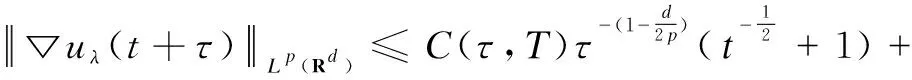
Similarly, takingτ=T=t=1 and using Gronwall Lemma, the inequality(7) is established.
Whenr∈[d,∞), taking theLrnorm of the identity(41), and from the inequalities(39) and(40) again, we have
wheret∈(0,T],p>d. Therefore,
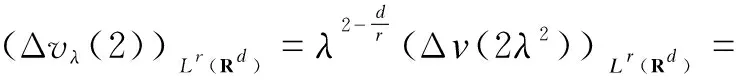
and the corollary is proven.
5 Conclusions

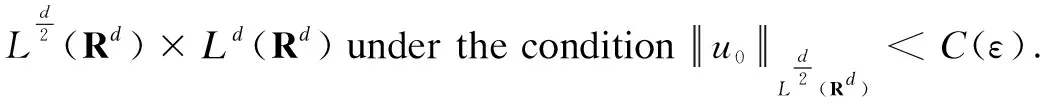
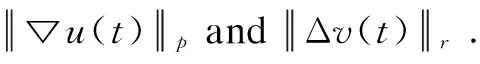
 Journal of Donghua University(English Edition)2022年1期
Journal of Donghua University(English Edition)2022年1期
- Journal of Donghua University(English Edition)的其它文章
- Sentiment Lexicon Construction Based on Improved Left-Right Entropy Algorithm
- Expert Knowledge-Based Apparel Recommendation Question and Answer System
- Molecular Modulation of Structure and Ferroelectric Performance of Poly(vinylidene fluoride) Free Standing Films from Aspects of Molecular Weight and Crystallization Temperature
- Theoretical Calculation and Analysis of Muffler Based on Multilayer Sound Absorbing Material
- Preparation of Polyaniline/Cellulose Nanofiber Aerogel for Efficient Removal of Cr(VI) from Aqueous Solution
- Consensus for High-Order Linear Multi-Agent Systems with Unknown but Bounded Measurement Noises
