Consensus for High-Order Linear Multi-Agent Systems with Unknown but Bounded Measurement Noises
YANG Ting(楊 婷), KANG Jianling(康劍靈), WANG Yumeng(王雨蒙)
College of Science, Donghua University, Shanghai 201620, China
Abstract: The static ε-consensus problem for a high-order linear multi-agent system is studied over a connected undirected communication topology, in which the state measurements of neighbors are affected by unknown but bounded(UBB) noises. Using the dead-zone function and binomial coefficients, we propose a distributed consensus protocol. Under this protocol, all agents achieve static ε-consensus, i. e., the first components of the states for each agent reach ε-consensus, and the remaining components reach agreement at zero. Numerical examples illustrate the validity of the theoretical results.
Key words: cooperative control; static ε-consensus; measurement noise; dead-zone function; multi-agent system
Introduction
A multi-agent system consists of multiple agents with certain perception and communication capabilities. Agents communicate and collaborate with each other to accomplish tasks that cannot be accomplished by a single agent. Consensus problem is the primary condition for cooperative control of multi-agent systems. The so-called consensus means that each agent in a multi-agent system transmits information according to some control protocols, and the states of all agents eventually converge to equilibrium points over time[1-2]. Consensus has become a popular research topic in multi-agent systems, which is widely used in broad fields such as unmanned aerial vehicles, intelligent transportation, and distributed sensor networks, with important research and application values[1-5].
Numerous existing literature considers the case without noises in the state measurements of the neighbors,i.e., the states of the neighbors can be obtained accurately. However, in the actual system, each agent cannot accurately measure the states of its neighbors because the states of neighbors are affected by factors such as noise, time delay, and communication topology. Therefore, the state measurements of neighbors are generally considered as disturbed quantities, and only a small amount of literature has investigated the presence of noise in the state measurements of neighbors[6-8]. Moreover, most of the literature considering the measurement noise assumes that the noise is a random variable[9-11]. However, not all the noises in the system can be treated as a random variable. For some noises, it is only known that it belongs to a given set and has no statistical properties or probability distribution. The unknown but bounded (UBB) measurement noises[7, 12]are involved in filtering, identification and robust control theory in mobile robots, drones, data fusion and other fields.
Bausoetal.[7]studied that the first-order multi-agent system with UBB measurement noises could achieveε-consensus, in which the communication topology was connected and undirected. They proposed a distributed consensus protocol called “l(fā)azy rules”. The states of all agents will converge to the equilibrium points in the target set with a radiusε.
Huetal.[8]discussed that the second-order multi-agent system with UBB measurement noises could achieve static consensus through “l(fā)azy rules” over connected and undirected communication topology, where the positions of neighbors could be accurately measured, and UBB noises only existed in the velocity measurements.
Mengetal.[13-14]studied the staticε-consensus problem of the second-order and the third-order multi-agent systems with UBB measurement noises under connected and undirected communication topology. That is, the velocities of all agents reached consensus at zero and their positions achievedε-consensus. They designed two consensus protocols by using and not using neighbor’s velocity information, respectively, both of which made the multi-agent system achieve staticε-consensus.
In the above research, the dynamics of agents only considered the case of a single integrator, double integrators and triple integrators. However, for some actual systems, we need to consider not only relative position and velocity information, but also more information, for example acceleration when establishing a consensus protocol. Therefore, the consensus problem for high-order linear multi-agent systems shows more practical significance and development prospects[15-16].
In this paper, we will design a distributed consensus protocol under connected and undirected communication topology to achieve the staticε-consensus for a high-order linear multi-agent system with UBB measurement noises. The first component of the agent state achievesε-consensus, namely, the position components asymptotically converge to the target set with a radiusε, and the remaining components reach agreement at zero.
The remainder of this paper is organized as follows. Section 1 recalls some preliminaries in graph theory. Section 2 reviews the results on staticε-consensus of second-order agents with UBB measurement noises. The staticε-consensus problem of high-order agents with UBB measurement noises is then formulated. Section 3 presents distributed consensus protocols. Staticε-consensus is then established under the consensus protocols. Section 4 provides numerical examples to verify the theoretical results. Section 5 concludes the paper.
1 Preliminaries
2 Problem Staement
The staticε-consensus for a class of multi-agent systems with UBB measurement noises is introduced in Refs. [7, 13-14]. In Ref. [13], the staticε-consensus for a second-order multi-agent system consisting ofNagents is considered. The dynamics of each agenti(i∈I[1,N]) is determined by the second-order integrators
(1)
wherexi∈R,vi∈Randui∈Rare position, velocity, and control input of the agenti, respectively. Assume that all agents can measure their own states accurately. Consider the case that UBB measurement noises are present in neighbors’ states, that is,
(2)
wherej∈Ni,i∈I[1,N],xijandvijare respectively position and velocity of the agentj, measured by the agenti, anddxijanddvijare continuous UBB measurement noises and satisfy
(3)
wheret≥0;ξx≥0 andξv≥0 are known constants. Letx=(x1,x2, …,xN)T∈RN,v=(v1,v2, …,vN)T∈RN.
Definition1(Staticε-consensus[13]) The multi-agent system (1) with UBB measurement noises is said to achieve staticε-consensus if agents’ velocities achieve consensus at zero and agents’ positions achieveε-consensus,i.e.,

For each agenti,i∈I[1,N], Mengetal.[13]proposed the following distributed consensus protocol,
(4)
where
(5)
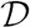
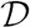
(6)
Then the closed-loop dynamics of the agentiis
(7)
Their results can be stated in the following theorem.
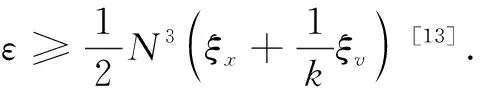
In this paper, we consider a networked multi-agent system consisting ofNagents with identical dynamics. The high-order integral dynamics of each agent is described by
(8)
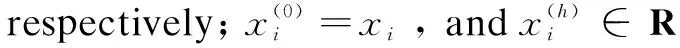
Assumption1The graph associated with the communication topology is connected and undirected.
Assume that each agent can measure its own state accurately and UBB measurement noises are present in the measurements of neighbors’ states,i.e.,
(9)

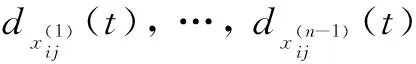
for allt≥0 , wheredx(m)≥0,m=0, 1, …,n-1 are known constants.
Definition2The multi-agent system (8) with UBB measurement noises is said to achieve staticε-consensus if the first components of agent statesxi(t)(i=1, 2, …,N)achieveε-consensus and remaining components achieve consensus at zero,i.e.,

3 Main Results
In this section, we are inspired by the control protocol (4) to give a design analysis for high-order linear multi-agent system (8) to achieve staticε-consensus. Let
(10)
We propose the following distributed consensus protocol for each agenti(i=1, 2, …,N),

(11)
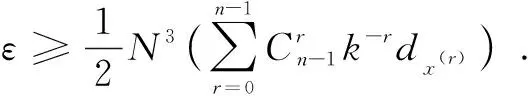
Proof Under the consensus protocol (11), from Eq. (10) we know that
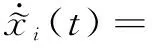
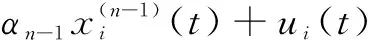

(12)
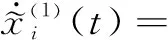
Similarly, we can obtain
(13)
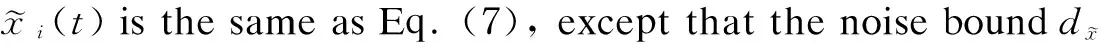
According to Theorem 1, if Assumption 1 and Assumption 2 are satisfied, then
and
(14)
(15)
From the equation
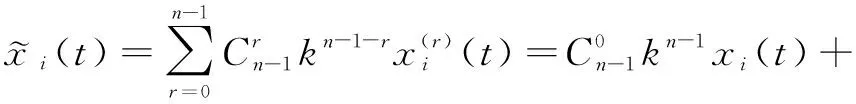
we have

We conclude that
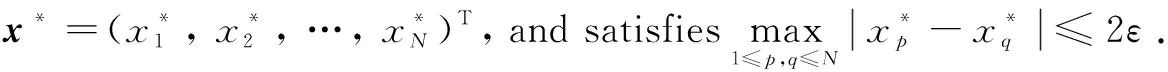
Remark1Compared with the second-order consensus protocol (4), whenn=2, andα0=α1=0 in the high-order consensus protocol (11), the high-order linear multi-agent system (8) can be written as
The corresponding consensus protocol (11) is
4 Numerical Examples
We consider a fourth-order multi-agent system with six interacting agents described by multi-agent system (8). The communication topology among agents is shown in Fig. 1, and the corresponding Laplacian matrix is
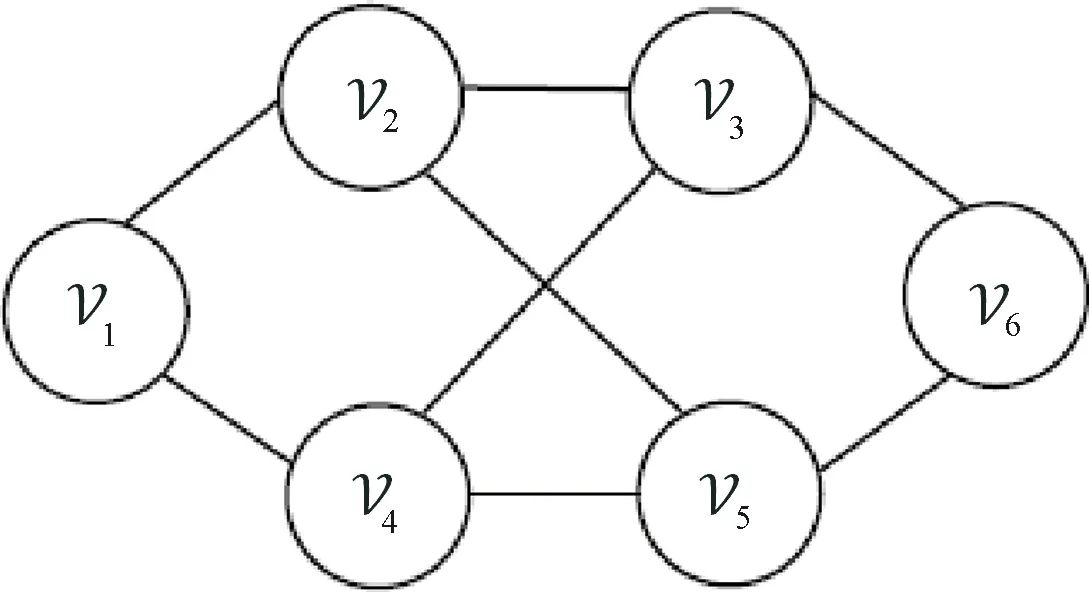
Fig. 1 Communication topology
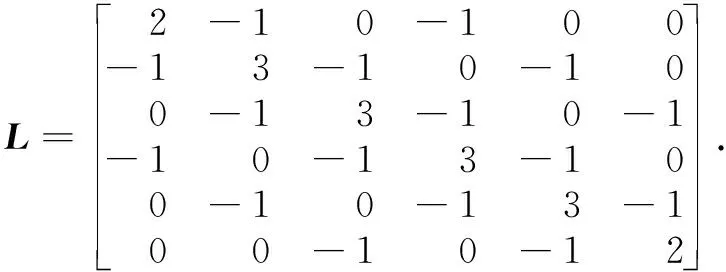

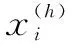

Fig. 2 Evolutions of the states of all agents under the consensus protocol (11): (a) trajectories of xi; (b) trajectories of
5 Conclusions
In this paper, we studied the staticε-consensus problem for high-order linear multi-agent systems with UBB measurement noises. For a general high-order linear multi-agent system, the high-order standard form of the system can be obtained through coordinate transformation. We analyzed the standard form of the system and extended the existing second-order staticε-consensus protocol to agents with high-order integrator dynamics. Staticε-consensus for the multi-agent system was achieved under the consensus protocol that we proposed.
 Journal of Donghua University(English Edition)2022年1期
Journal of Donghua University(English Edition)2022年1期
- Journal of Donghua University(English Edition)的其它文章
- Sentiment Lexicon Construction Based on Improved Left-Right Entropy Algorithm
- Expert Knowledge-Based Apparel Recommendation Question and Answer System
- Molecular Modulation of Structure and Ferroelectric Performance of Poly(vinylidene fluoride) Free Standing Films from Aspects of Molecular Weight and Crystallization Temperature
- Global Existence and Decay of Solution to Parabolic-Parabolic Keller-Segel Model in Rd
- Theoretical Calculation and Analysis of Muffler Based on Multilayer Sound Absorbing Material
- Preparation of Polyaniline/Cellulose Nanofiber Aerogel for Efficient Removal of Cr(VI) from Aqueous Solution
