孫孔浩 易為

(中國(guó)科學(xué)技術(shù)大學(xué),中國(guó)科學(xué)院量子信息重點(diǎn)實(shí)驗(yàn)室,合肥 230026)

非厄米拓?fù)湎到y(tǒng)的拓?fù)洳蛔兞靠梢杂啥x在雙正交基下的局域拓?fù)渲笜?biāo)刻畫(huà).不同于厄米體系,非厄米局域拓?fù)渲笜?biāo)在動(dòng)力學(xué)過(guò)程中的傳播和演化目前還未見(jiàn)文獻(xiàn)討論.本文研究非厄米拓?fù)潴w系局域拓?fù)渲笜?biāo)的動(dòng)力學(xué)特性,重點(diǎn)關(guān)注淬火過(guò)程中,局域拓?fù)渲笜?biāo)由邊界向體內(nèi)的傳播.結(jié)果表明,當(dāng)淬火前后的體系拓?fù)湫再|(zhì)不同時(shí),系統(tǒng)中存在局域拓?fù)渲笜?biāo)的流動(dòng),其流速與體系群速度相關(guān),但具體形式與相應(yīng)厄米體系不同.以3 個(gè)具體模型為例,通過(guò)數(shù)值計(jì)算說(shuō)明了這一結(jié)論.其中,對(duì)于特定具有非厄米趨膚效應(yīng)的模型,可以發(fā)現(xiàn)局域拓?fù)渲笜?biāo)的流速上限與廣義布里淵區(qū)中的群速度直接相關(guān).但這一關(guān)系在其他非厄米模型中則需要修正,其更普適的形式有待進(jìn)一步研究.本文的結(jié)果揭示了非厄米體系中局域拓?fù)渲笜?biāo)傳播的復(fù)雜性,是進(jìn)一步理解非厄米局域拓?fù)渲笜?biāo)動(dòng)力學(xué)行為的基礎(chǔ).

1 引言

非厄米拓?fù)潴w系是近年來(lái)凝聚態(tài)及量子模擬領(lǐng)域的研究熱點(diǎn)之一[1-6].非厄米拓?fù)淠Ｐ兔撎ビ陂_(kāi)放系統(tǒng)[7,8],其性質(zhì)與封閉系統(tǒng)厄米模型多有不同.其中尤為典型的例子是具有非厄米趨膚效應(yīng)的拓?fù)淠Ｐ蚚9-21].在開(kāi)邊界條件下,該類(lèi)體系的本征態(tài)波函數(shù)局域在邊界上,并在實(shí)空間呈能態(tài)依賴的指數(shù)分布;同時(shí)體系本征能譜在復(fù)平面上的分布受邊界條件影響.與此對(duì)應(yīng),在具有非厄米趨膚效應(yīng)的拓?fù)潴w系中,傳統(tǒng)的體邊對(duì)應(yīng)關(guān)系失效—定義于周期邊界布里淵區(qū)上的拓?fù)洳蛔兞坎辉倌軠?zhǔn)確預(yù)測(cè)開(kāi)邊界下的拓?fù)溥吘墤B(tài).為解釋這一現(xiàn)象,非布洛赫能帶論應(yīng)運(yùn)而生[9,10,14].根據(jù)該理論,非厄米拓?fù)湎到y(tǒng)在開(kāi)邊界條件下的性質(zhì)應(yīng)由計(jì)入了非厄米趨膚效應(yīng)的廣義布里淵區(qū)決定,而在廣義布里淵區(qū)上定義的非布洛赫拓?fù)洳蛔兞縿t保證了體邊對(duì)應(yīng)關(guān)系在非厄米系統(tǒng)中仍然成立.目前,非厄米趨膚效應(yīng)及非厄米能帶論在一系列經(jīng)典或量子的人工拓?fù)潴w系中被相繼觀測(cè)證實(shí)[22-25].同時(shí),研究者發(fā)現(xiàn),非布洛赫能帶論及廣義布里淵區(qū)也在非布洛赫宇稱(chēng)-時(shí)間對(duì)稱(chēng)性及非布洛赫淬火動(dòng)力學(xué)等方面有重要應(yīng)用[26-30].

另一方面,人們發(fā)現(xiàn)不論非厄米體系是否具有趨膚效應(yīng),其拓?fù)洳蛔兞烤赏ㄟ^(guò)定義在雙正交基下的局域拓?fù)渲笜?biāo)刻畫(huà)[31,32],而后者可以通過(guò)動(dòng)力學(xué)過(guò)程中的可觀測(cè)量在實(shí)驗(yàn)上進(jìn)行觀測(cè)[30].對(duì)局域拓?fù)渲笜?biāo)的研究起源于厄米拓?fù)潴w系[33-36].在這些模型中,雖然體系具有能帶拓?fù)浼巴負(fù)浔Ｗo(hù)的邊緣態(tài)等全局特性,定義在體態(tài)上的局域拓?fù)渲笜?biāo)卻是量子化的,能反映體系的全局拓?fù)涮匦?并在拓?fù)湎嘧兏浇尸F(xiàn)特定的標(biāo)度行為.更進(jìn)一步,文獻(xiàn)[34]通過(guò)對(duì)厄米體系淬火動(dòng)力學(xué)的研究,發(fā)現(xiàn)了動(dòng)力學(xué)過(guò)程中局域拓?fù)渲笜?biāo)在體系內(nèi)部的傳播規(guī)律.例如,當(dāng)體系從拓?fù)浞瞧接沟某鯌B(tài)出發(fā),由拓?fù)淦接沟墓茴D量驅(qū)動(dòng)進(jìn)行時(shí)間演化時(shí),初始體系內(nèi)部量子化的局域拓?fù)渲笜?biāo)在一定時(shí)間后會(huì)受到始于邊界的局域拓?fù)渲笜?biāo)流影響,在某弛豫時(shí)間t*后明顯偏離量子化取值.通過(guò)對(duì)該弛豫時(shí)間t*進(jìn)行分析,研究者發(fā)現(xiàn)局域拓?fù)渲笜?biāo)在淬火過(guò)程中的傳播速度與體系群速度相關(guān).這揭示了局域拓?fù)渲笜?biāo)在厄米拓?fù)潴w系非平衡動(dòng)力學(xué)過(guò)程中的普適行為,具有重要意義.與此對(duì)應(yīng),非厄密拓?fù)潴w系的局域拓?fù)渲笜?biāo)是否具有類(lèi)似的行為,還未見(jiàn)研究報(bào)道.

在這一背景下,本文研究非厄米拓?fù)淠Ｐ偷木钟蛲負(fù)渲笜?biāo)在淬火過(guò)程中的動(dòng)力學(xué)行為.首先驗(yàn)證說(shuō)明了定義在雙正交基下的局域拓?fù)渲笜?biāo)可以有效刻畫(huà)對(duì)應(yīng)非厄米體系的全局拓?fù)湫再|(zhì),并在拓?fù)湎噙吔绺浇尸F(xiàn)普適的臨界行為.對(duì)于淬火動(dòng)力學(xué),考慮初態(tài)為某初始哈密頓量Hi的本征態(tài),在末態(tài)哈密頓量Hf的驅(qū)動(dòng)下做時(shí)間演化.一般而言,Hi和Hf參數(shù)不同,且處于不同拓?fù)湎鄥^(qū).以幾個(gè)具體的非厄米拓?fù)淠Ｐ蜑槔?計(jì)算了淬火動(dòng)力學(xué)演化過(guò)程中,非厄米局域拓?fù)渲笜?biāo)的演化,并通過(guò)擬合確定了局域拓?fù)渲笜?biāo)從邊界向體系內(nèi)部傳播的速度.對(duì)于本文考察的具有非厄米趨膚效應(yīng)的模型,可以發(fā)現(xiàn)該傳播速度與定義在廣義布里淵區(qū)中的群速度相關(guān),而與定義于一般布里淵區(qū)的群速度無(wú)關(guān).然而,對(duì)于一般性的非厄米模型,該結(jié)論并不普遍成立.一般說(shuō)來(lái),在非厄米體系中局域拓?fù)渲笜?biāo)的傳播速度與群速度相關(guān),但二者之間的關(guān)系是否普適則需要進(jìn)一步研究.

下面首先以一解析可解的非厄米拓?fù)淠Ｐ蜑槔?說(shuō)明非厄米局域拓?fù)渲笜?biāo)對(duì)非厄米拓?fù)淠Ｐ偷倪m用性及其臨界行為.然后討論該模型的淬火動(dòng)力學(xué)過(guò)程中,局域拓?fù)渲笜?biāo)的演化及傳播速度.最后,通過(guò)對(duì)其他具體非厄米拓?fù)淠Ｐ痛慊饎?dòng)力學(xué)的計(jì)算,對(duì)局域拓?fù)渲笜?biāo)傳播速度的一般性規(guī)律進(jìn)行討論.

2 非厄米局域拓?fù)渲笜?biāo)

為說(shuō)明非厄米局域拓?fù)渲笜?biāo)的特性,考慮二維正方晶格上的非厄米哈密頓量

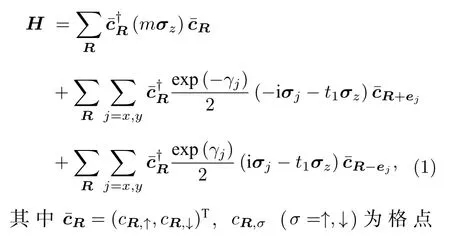
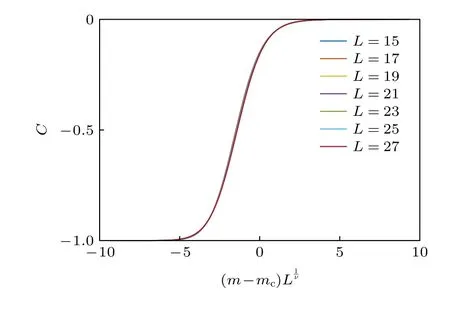
圖1 非厄米局域拓?fù)渲笜?biāo)的標(biāo)度行為.系統(tǒng)中心的非厄米局域拓?fù)渲笜?biāo)隨著 m 的變化遵循的標(biāo)度行 為.在 L 分別取 15,17,19,21,23,25,27等值時(shí)(對(duì) 應(yīng)于圖中不同顏色的曲線),所有曲線經(jīng)變換后遵循同一函數(shù)形式,經(jīng)擬合得到 ν≈1.1259.在本文的數(shù)值計(jì)算中,取t1=1,γx=γy=0.3Fig.1.Scaling behavior of the non-Hermitian local topological marker near the topological phase transition.The numerically calculated local topological markers for different system sizes (L=15,17,19,21,23,25,27) collapse to the same curve,with the functional formand ν≈1.12(6).For all calculations,we take t1=1 ,γx=γy=0.3.

3 非厄米局域拓?fù)渲笜?biāo)的動(dòng)力學(xué)行為

考慮(1)式哈密頓量的淬火過(guò)程中,非厄米局域拓?fù)渲笜?biāo)的動(dòng)力學(xué)行為.設(shè)初始時(shí)刻體系由哈密頓量Hi(t1,m) 描述,且其下能帶被完全占據(jù).在此后的時(shí)間演化中,哈密頓量變?yōu)?則相應(yīng)投影算符均隨時(shí)演化,從而導(dǎo)致非厄米局域拓?fù)渲笜?biāo)的演化.對(duì)于厄米拓?fù)潴w系,研究者發(fā)現(xiàn),當(dāng)初末哈密頓量拓?fù)湫再|(zhì)不同時(shí),具有開(kāi)放邊界的體系在淬火過(guò)程中會(huì)出現(xiàn)局域拓?fù)渲笜?biāo)的流動(dòng),其流速與群速度相關(guān)[34].這里我們關(guān)心的第一個(gè)問(wèn)題是,在具有非厄米趨膚效應(yīng)的非厄米拓?fù)潴w系中,是否有類(lèi)似的結(jié)論.

如圖2所示,數(shù)值計(jì)算了L=23 的開(kāi)邊界二維晶格體系中,各格點(diǎn)的非厄米局域拓?fù)渲笜?biāo)在不同時(shí)刻的行為.選擇的初始哈密頓量處于拓?fù)浞瞧接箙^(qū)間(C=-1),末態(tài)哈密頓量處于拓?fù)淦接箙^(qū)間(C=0).在t=0時(shí)刻,局域拓?fù)渲笜?biāo)C在體系中心取-1,而在邊界上取正值,這是因?yàn)榫钟蛲負(fù)渲笜?biāo)對(duì)格點(diǎn)求和應(yīng)該始終得 0.而在t ＞0 時(shí)刻,局域拓?fù)渲笜?biāo)開(kāi)始從邊界向體內(nèi)流動(dòng)(見(jiàn)圖2(a)),系統(tǒng)中心處的局域拓?fù)渲笜?biāo)會(huì)在某個(gè)特征時(shí)間t*后明顯偏離其量子化取值.由t*與系統(tǒng)尺寸的線性關(guān)系,可以定義并計(jì)算局域拓?fù)渲笜?biāo)的的傳播速度.在具體數(shù)值計(jì)算中,取時(shí)間演化的步長(zhǎng)為0.02(這里時(shí)間單位為 1/t1),定義t*為體系中心處局域拓?fù)渲笜?biāo)對(duì)時(shí)間的差分首次超過(guò)閾值的時(shí)間.數(shù)值上,取閾值為 10-3.在得到不同系統(tǒng)尺寸下的t*后,通過(guò)線性擬合,得到局域拓?fù)渲笜?biāo)的傳播速度vlcm.由圖2(b)可以看出,在該模型下,非厄米局域拓?fù)渲笜?biāo)的傳播速度與廣義布里淵區(qū)下得到的最大值相符(黃線),而與周期邊界下布里淵區(qū)里計(jì)算的群速度(紅星)不同.這里廣義布里淵區(qū)上的群速度定義為相應(yīng)地,一般布里淵區(qū)上的群速度定義為vix=Re(?Ei(k)/?kx).這似乎意味著只需要利用非布洛赫能帶論便可解釋及預(yù)言非厄米拓?fù)潴w系淬火過(guò)程中局域拓?fù)渲笜?biāo)流的動(dòng)力學(xué)演化.

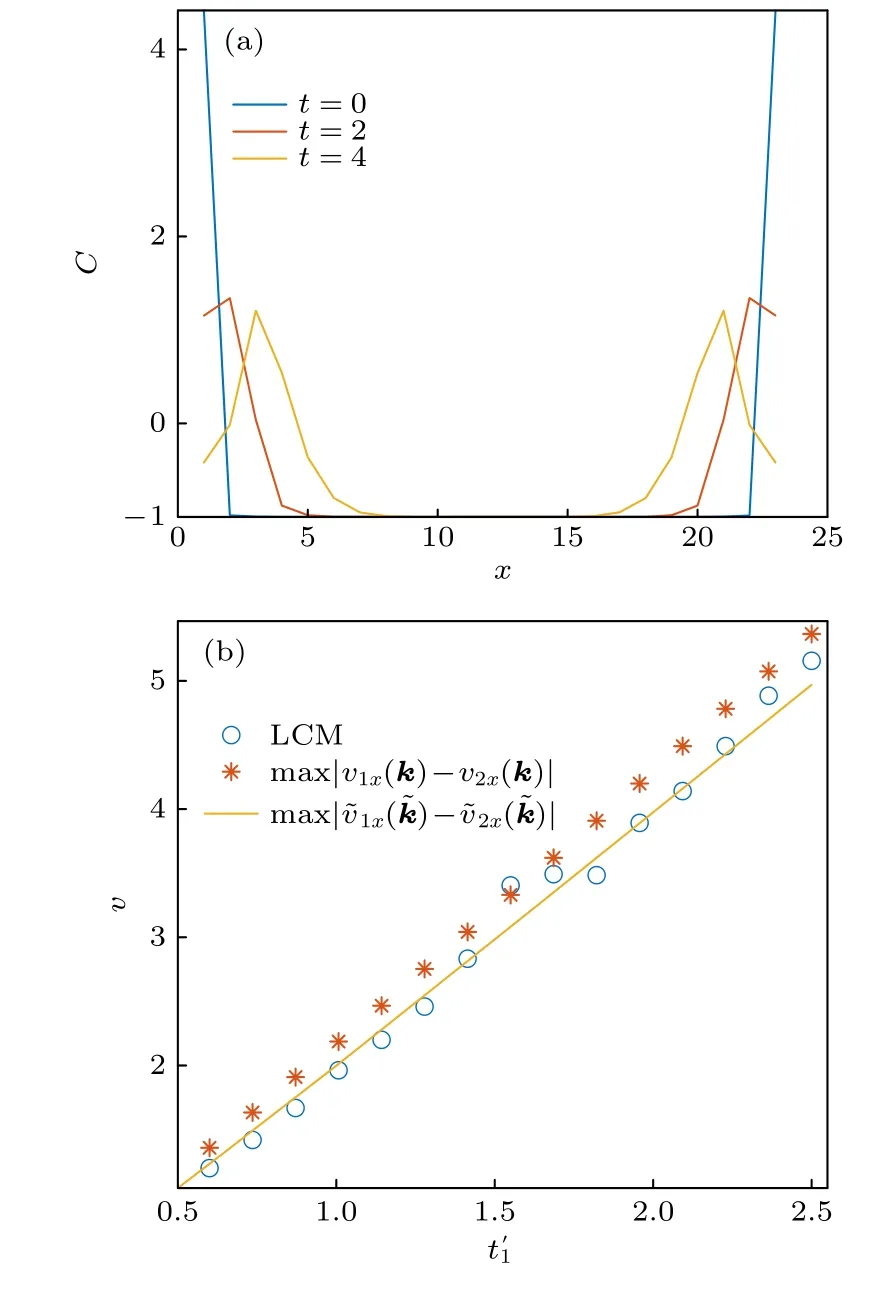
圖2 非厄米局域拓?fù)渲笜?biāo)的傳播速度 (a) 淬火過(guò)程中系統(tǒng)中心格點(diǎn)處的非厄米局域拓?fù)渲笜?biāo)的時(shí)間演化.系統(tǒng)尺寸為L(zhǎng)=23,取開(kāi)邊界.初始時(shí)H(t1=1,m=1)處于拓?fù)浞瞧接瓜?淬火后H(1,m′=6)處于拓?fù)淦接瓜?淬火前后 γx=γy=0.3.這里只考慮 x 方向的動(dòng)力學(xué)演化,y 方向的演化有類(lèi)似性質(zhì).(b) 非厄米局域拓?fù)渲笜?biāo)的傳播速度隨末態(tài)哈密頓量參數(shù)的變化.淬火參數(shù)與圖(a)相同.分別數(shù)值模擬了體系大小為L(zhǎng)=11,15,19,23,27時(shí)的淬火過(guò)程,并通過(guò)線性擬合 t* 與 L 的關(guān)系,數(shù)值得到了局域拓?fù)渲笜?biāo)的傳播速度Fig.2.Dynamics of the non-Hermitian local topological marker.(a) Spatial distribution (along the x -direction) of the non-Hermitian local topological marker at different times of the quench dynamics.The parameters are: L=23,Hi(t1=1,m=1),Hf(=1,m′=6),γx=γy=0.3.(b) Propagation speed of the local topological marker as a function of .Other parameters are the same as those in panel (a).

4 其他非厄米拓?fù)湎到y(tǒng)的局域拓?fù)渲笜?biāo)流

為驗(yàn)證上述結(jié)論的普適性,本節(jié)考察其他非厄米拓?fù)淠Ｐ偷拇慊疬^(guò)程.首先考慮如下具有非厄米趨膚效應(yīng)的非厄米Qi-Wu-Zhang 模型:

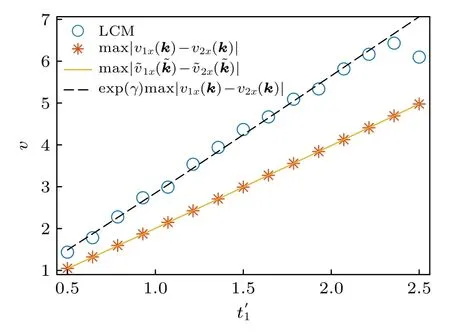
圖3 模型(5)的非厄米局域拓?fù)渲笜?biāo)的傳播速度隨的變化.初始時(shí),tx=ty=1,m=1;淬火后,==,m′=6.淬火前后γx=γy=γ=0.35Fig.3.Propagation speed of the non-Hermitian local topological marker for Hamiltonian (5).We fix γx=γy=γ=0.35,and the pre-and post-quench parameters aretx=ty=1,m=1and ==,m′=6,respectively.

最后考慮如下非厄米模型:

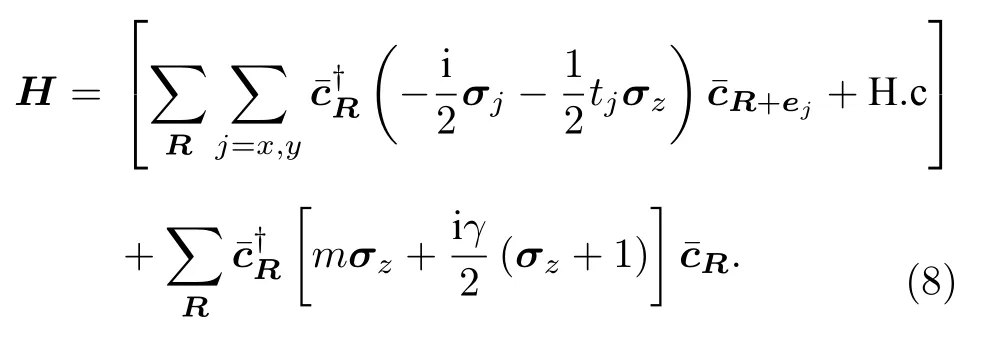
與前面討論的兩個(gè)模型不同,哈密頓量(8)不具有非厄米趨膚效應(yīng).如圖4所示,在該模型淬火過(guò)程中,局域拓?fù)渲笜?biāo)的傳播速度要大于定義在一般布里淵區(qū)的群速度.但不同于模型(5)的指數(shù)加速,數(shù)值上看,局域拓?fù)渲笜?biāo)傳播速度與max|v1x(k)-v2x(k)|相比,相差一個(gè)常數(shù).

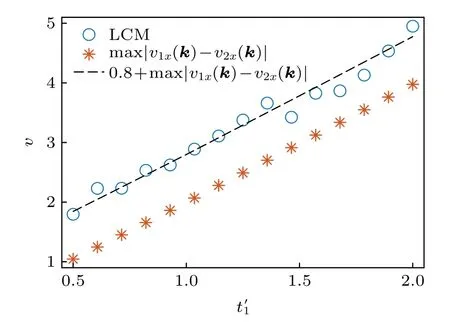
圖4 模型(8)的非厄米局域拓?fù)渲笜?biāo)的傳播速度隨的變化.初始時(shí),tx=ty=1,m=1;淬火后,==,m′=6.淬火前后γ=0.3Fig.4.Propagation speed of the non-Hermitian local topological marker for Hamiltonian (8).We fix γ=0.3,and the pre-and post-quench parameters aretx=ty=1,m=1 and ==m′=6,respectively.

5 總結(jié)與展望

本文研究了非厄米拓?fù)淠Ｐ椭蟹嵌蛎拙钟蛲負(fù)渲笜?biāo)的性質(zhì).首先刻畫(huà)了非厄米局域拓?fù)渲笜?biāo)在非厄米拓?fù)湎嘧兏浇呐R界行為,數(shù)值確定了其臨界系數(shù).然后考察了3 個(gè)不同非厄米拓?fù)淠Ｐ偷膭?dòng)力學(xué)淬火過(guò)程,計(jì)算了非厄米局域拓?fù)渲笜?biāo)的傳播速度.與厄米拓?fù)潴w系類(lèi)似,當(dāng)淬火前后的體系拓?fù)湫再|(zhì)不同時(shí),系統(tǒng)的淬火過(guò)程中存在局域拓?fù)渲笜?biāo)的流動(dòng).發(fā)現(xiàn)局域拓?fù)渲笜?biāo)的傳播速度與體系群速度相關(guān),但其關(guān)系并不普適.具體而言,對(duì)于本文考察的3 個(gè)模型,局域拓?fù)渲笜?biāo)的傳播速度或與定義于廣義布里淵區(qū)上的群速度直接相關(guān),或與群速度差一個(gè)指數(shù)因子,或差一常數(shù).本文的結(jié)果揭示了非厄米體系中局域拓?fù)渲笜?biāo)傳播的復(fù)雜性,為進(jìn)一步理解非厄米局域拓?fù)渲笜?biāo)的動(dòng)力學(xué)行為打下了基礎(chǔ).

局域拓?fù)渲笜?biāo)傳播速度的非普適行為或與不同模型中非厄米性出現(xiàn)的不同形式有關(guān).具體而言,在本文的3 個(gè)非厄米模型中,唯有第一個(gè)模型在開(kāi)邊界時(shí)具有純實(shí)數(shù)本征能譜.因此,一個(gè)合理的猜想是,局域拓?fù)渲笜?biāo)的傳播速度能否由廣義布里淵區(qū)上的群速度刻畫(huà),與體系在開(kāi)邊界下本征能譜的虛實(shí)有關(guān).在今后的研究中,我們將進(jìn)一步考察這一猜想的正確性.同時(shí),為進(jìn)一步理解非厄米局域拓?fù)渲笜?biāo)的傳播,可以研究由主方程描述的開(kāi)放體系動(dòng)力學(xué)過(guò)程中局域拓?fù)渲笜?biāo)的演化.基于非厄米模型與開(kāi)放體系的密切關(guān)系,期望通過(guò)這一角度,更徹底地理解非厄米局域拓?fù)渲笜?biāo)的非普適傳播行為.