Theory of multiphoton photoemission disclosing excited states in conduction band of individual TiO2 nanoparticles?
Bochao Li(李博超), Hao Li(李浩), Chang Yang(楊暢), Boyu Ji(季博宇),Jingquan Lin(林景全), and Toshihisa Tomie(富江敏尚)
School of Science,Changchun University of Science and Technology,Changchun 130022,China
Keywords: multiphoton photoemission,nanoparticles,thermal emission,TiO2
1. Introduction
Bulk gold (Au) is the highest chemically inert metal,[1]but nano-sized Au nanoparticle(NP)is one of the most chemically active materials.[2]Understanding how a chemically inert material changes to a highly active catalyst is a major topic in nanoscience.[3-14]Previous papers assumed the Fermi level as the ground state of energetic electrons, called “hot electrons”,[7,10-13]which means that the barrier height, ?E,for electron transfer is the same in NPs and bulk. Then,there is no advantage of NPs over bulk materials in terms of electron transfer. We are proposing[15,16]that high chemical activities of NPs originate in the generation of excited states in the conduction band, by which ?Eis lowered in NPs. TiO2is one of the most important materials as catalysts and its properties were studied by many people.[17-22]The number of papers discussing dye-sensitized nanocrystalline TiO2as a low-cost high-efficiency solar cell increased exponentially since 1990.[23-26]Presently,perovskite-type solar cells(PSC)are studied and most PSCs use TiO2as an electron transfer layer.[27-32]
When studying electron transfer in NPs, observing individual NP is important as was emphasized by Beaneet al.[33]Photoemission electron microscopy (PEEM) having tens-nm spatial resolution[34,35]is one of the best tools for studying electron transfer reactions in individual NPs. PEEM observes electrons ejected into the vacuum, and multiphoton photoemission(m-PPE)is a powerful technique for ejecting electrons into the vacuum.[36-42]We found an excited state in TiO2NPs at 0.78 eV above the conduction band minimum by using the two-color pump-probe technique using the fundamental and second harmonic of a femtosecond laser.[15,16]The lifetime of the discovered excited state was longer than 4 ps, which is a few orders of magnitude longer than the lifetime reported for single crystals. This finding strongly supports our claim that the secret of nanomaterials is in the generation of excited states having a long lifetime.
While the excited state having a long lifetime was discovered,there remained a mystery in our previous work.[15,16]The brightness of PEEM images monotonically decreased with the excitation wavelength by as large as four orders of magnitude.When the ionization energy or the electron affinity isEg,electrons in the valence band or at the conduction band bottom are excited to vacuum by photons having photon energyhνlarger thanhν0=Eg/nwhen the excitation is ann-photon process. We can tell the number of photons from the slope of the dependence of particle brightness,B,on laser intensity,I,B=a(hν)Inin a log-log plot,wherea(hν)is called an excitation spectrum.When the photon energyhνis smaller thanhν0,one more photon is required for the ionization. The brightness of the(n+1)-photon process will be lower than then-photon process, and the brightness should make a big jump athν0.However, no jump was observed and the excitation spectruma(hν) monotonically increased at higher photon energy. The present theory was derived to solve the puzzle.
For reproducing the observed excitation spectrum we need to assume two conditions: (i)the electrons in the excited states are instantly thermalized and(ii)the number of(n+1)-photon ionized electrons is smaller than the number of energetic electrons in the thermal distribution tail of then-photon excited electrons.
The energy,E(k),of electrons in excited states disperses with the wavenumber,k,of electron motion as
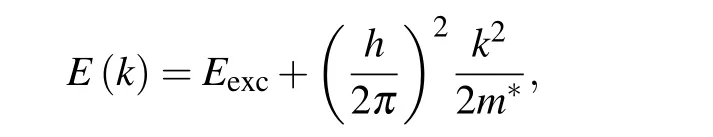
wherem?andhare an effective electron mass and the Planck constant.Eexcis the potential energy of the excited state and the second term is the kinetic energy of electrons. This dispersion was confirmed in angle-resolved electron emission measurements.[43-49]At high power laser illumination for observing higher-orderm-PPE,many electrons can coexist in excited states,and the energy distribution will follow the Boltzmann distribution by collisions among electrons. Thus, the first condition will be justified.
There are a large number of papers reporting two-photonm-PPE, 2PPE,[36-42]but few report higher-orderm-PPE withm> 2.[41]Only two[49,50]in our survey reported identical spectra for 2PPE and 3PPE, in which an intensity ratio of 3-PPE to 2PPE was about 10?4. Hence,if the temperature,kT,of the electron gas in the excited state is high enough so that exp(??E/kT)>10?4where ?Eis the energy difference of the excited state from the vacuum level, the thermal emission from the excited state overwhelms the emission of directly photo-excited electrons by absorbing one more photon.In fact,we reported that thermal emission dominated overm-PPE in the case of Au NPs.[51]As discussed in Ref.[51],nonintegerm-PPE reported in many papers[52-56]are explained by thermal emission. The present theory also explains why the number of reports ofm-PPE withmlarger than three is very few.[41]
The derived theory serves as a novel diagnostic of the excited state in the conduction band. The observed NPs were classified into two groups; three-photon (3-photon NPs) and four-photon excited particles (4-photon NPs). The parameter for fitting to the data of 4-photon NPs confirmed the Ti3d egstate close into the vacuum level located at 5.7 eV above the top of the valence band. The fitting parameter for 3-photon NPs confirmed a direct bandgap of 3.6 eV from O2p to Ti3d t2gat theXpoint in the Brillouin zone. These states are different from the state revealed by the two-color pump-probe technique.[15,16]
2. Theory of multiphoton photoemission
We considern-photon excitation of valence band electrons to the excited state atEGabove the valence band top as shown in Fig.1. Electrons with binding energyEBsmaller thanE0,where

are excited to the excited state. Here,hνis the photon energy and the binding energy is measured from the valence band top.

Fig. 1. N-photon excited electrons are instantly thermalized and electrons with kinetic energy exceeding ?E at the tail of the Boltzmann distribution escape into the vacuum. Excess energy above the excited state,Ek,heats the electron gas.
Expressing the density of states of the valence band asD(E),the number of electrons excited to the excited state,Ne,is given by
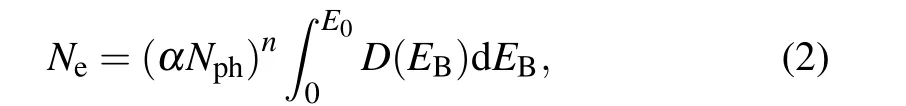
whereαis the one-photon absorption efficiency andNphis the number of photons irradiating the NP.For simplicity,αis assumed constant in alln-th excitation. The energyEB+EGis consumed to excite electrons to the excited state, and the excess energyEk=nhν ?(EB+EG)is stored in the electron gas as heat. The total heat energyEtotalis calculated as

The temperature is given by
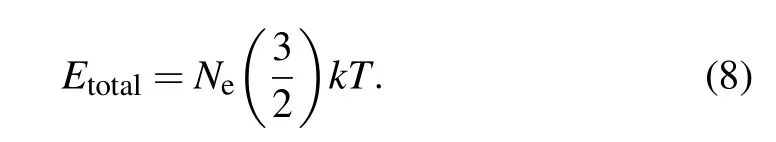
From Eqs.(5),(6),and(8),the temperatureTis obtained as

Electrons with the kinetic energy larger than ?E,defining the energy difference between the vacuum level and the ground state of the excited state, can escape into the vacuum. The number of escaped electronsNemitis given by

Absorption of laser energy by electrons in the excited states can raise the temperature of the electron gas. Previously, we observed this phenomenon in Au NPs at a high laser power.[51]However,the present theory ignores this additional heating for simplicity.
The above theory is valid under the following conditions.(I)The electrons in the excited states are instantly thermalized.This condition requires the excitation of many electrons in one NP.(II)The electron gas is not further heated by the laser.(III)The electron energy distribution follows the Boltzmann distribution.(IV)The number of(n+1)-photon-ionized electrons is smaller than the number of energetic electrons in the thermal distribution tail of then-photon excited electrons.
From Eq. (9), we know the temperature is independent of the laser intensity, whereas, in usual thermionic emission as observed in our previous study,[51]the emission intensity increases exponentially with the laser power which raises the temperature.
3. Experimental results
We illustrate how the theory reveals the excited states.Anatase TiO2NPs of nominal diameter 100 nm were sparsely dispersed on an n-type Si wafer as shown in Fig.2(a).The NPs were illuminated by 150-fs-width laser pulses and the electrons ejected into the vacuum were imaged by PEEM which has a nominal spatial resolution of 40 nm. The electron image was intensity-magnified by a microchannel plate (MCP),and the fluorescent image on the phosphor after the MCP was recorded by a charge-coupled device camera. The image brightness is proportional to the electron yield. The laser is tunable from 700 nm to 900 nm and operates at 76 MHz.The experimental method is detailed in our previous work.[15]
Figure 2(b) plots the brightnessversuslaser power at three wavelengths: 700 nm (circles), 760 nm (triangles), and 780 nm (stars). Most of the NPs yielded a 4-photon absorption slope with the rest yielding a 3-photon absorption slope.As representatives of the four-photon and three-photon excited particles, we selected NPs A and B, respectively, enclosed in the amber circles in Fig.2(a).
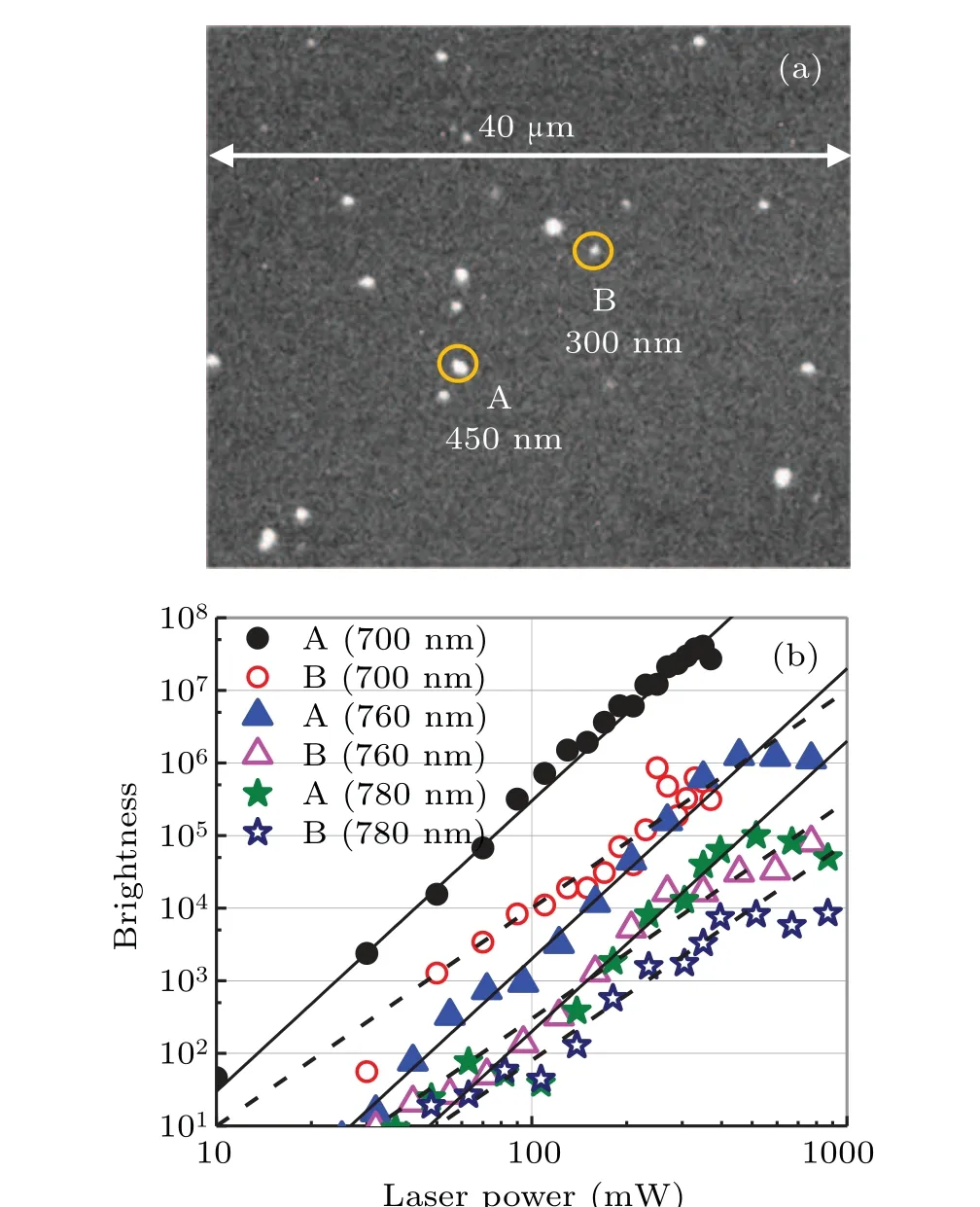
Fig. 2. (a) PEEM image of TiO2 NPs dispersed on a Si wafer. Two TiO2 NPs(A and B enclosed in amber circles)are selected as representative NPs.(b)Brightness versus laser power at three laser wavelengths. Filled and open symbols are the data of NP A and NP B, respectively. In most of the NPs(represented by NP A),the brightness increased with a 4-photon slope with the remaining NPs(represented by NP B)yielded a 3-photon slope.
The sizes of NP A and NP B were 3 pixels(450 nm)and 2 pixels (300 nm), respectively. Strictly speaking, both NPs are clusters of NPs,but here we call them NPs.
Figure 3 shows the wavelength dependence of the brightness at the 200-mW laser power for NPs A and B.The reference power of 200 mW for the excitation spectrum was chosen for the following two reasons. At power higher than 500 mW,the data points deviate from the linear slope in the log-log plot,and the reference power should be smaller than 500 mW. At lower power,NPs were darker and the accuracy of the brightness is poorer. So,higher reference power is better in terms of the reliability of the data. The electron yield decreased monotonically from 700 nm (1.78 eV) to 790 nm (1.57 eV). This result was unexpected for two reasons.First,the ionization energyEI=?E+EGfrom the valence band top is about 7.5 eV in TiO2.[57]Even for the oxygen-vacancy defect level lying at about 1 eV below the Fermi level,[17-22]the ionization energy is about 5.5 eV, which is larger than the energy of 4.71 eV for three photons of 1.57-eV light. The second was that the brightness monotonically decreased by as large as four orders of magnitude from 700 nm to 790 nm in NP A (a 4-photon slope NP).
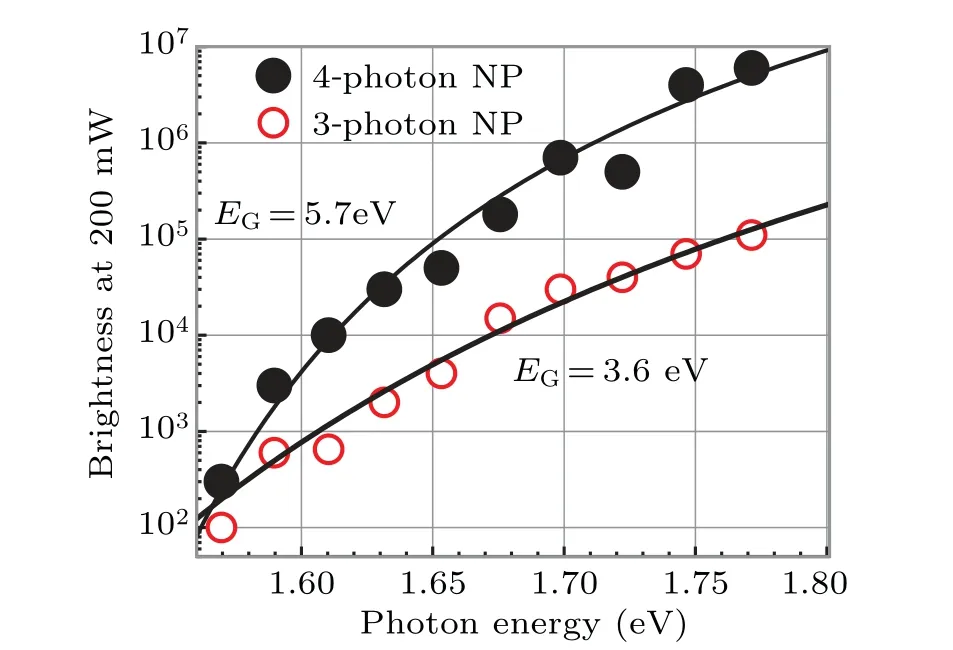
Fig.3. Photon-energy dependence of the electron yield of the two TiO2 NPs(A and B shown in Fig. 2(a)) under the 200-mW laser. The brightness increase(up to four orders of magnitude)is quite well reproduced by Eq.(11)(solid curves). The fitting parameter EG was 5.7 eV for NP A and 3.6 eV for NP B.
Although some resonance transition is possible,the resonance transition should manifest as discrete peaks rather than a monotonic increase. Furthermore,the resonance enhancement will be only about one order of magnitude.
Two mysteries are solved by the derived theory.As shown by the solid curves in Fig. 3, equation (11) quite well reproduces the observed excitation spectra. Here we assumed?E+EG=7.5 eV, the ionization energy given in Toyodaet al.[57]The best fittings were obtained withEGof 5.7 eV for NP A and 3.6 eV for NP B.
The three and four orders of magnitude differences in the brightness of NPs A and B at 700 nm (1.77 eV) and 790 nm(1.57 eV)were caused by theE0term(=nhν ?EG)in the exponential of Eq.(11). For example,whenn=4,?E=1.8 eV,andEG=5.7 eV,the value of exp(?4.5?E/E0)is 2.9×10?3at 700 nm,and 8.1×10?7at 790 nm. The factorE20in Eq.(11)further widens the brightness difference. Whennhνis close toEG,E0=nhν ?EGis small, the temperaturekTof the electron gas is low,and the number of thermally excited electrons that can escape into the vacuum reduces drastically. Because electrons are thermally excited from the excited state,nhνcan be smaller than the ionization energy. Even at the shortest wavelength in our experiment(700 nm), the 4-photon energy of 7.08 eV was below the ionization energy of 7.5 eV. In addition,although NP B was dark,some electrons in the valence band were ejected into the vacuum with a total photon energy of only 4.71 eV for three photons of 790-nm light. Therefore,thermionic emission has a great effect on photoemission.Thermionic emission has not been discussed in the past.[52-56]
4. Discussion
First, we comment on the accuracy of the fitting parameterEG. As discussed above, the rapid drop of brightness at smaller photon energy in Fig. 3 was caused by the decreased excess energyE0=nhν ?EGin the exponential of Eq. (11).The choices of ?Eand the parameterphave only a small effect on the value ofEG.In fitting the data in Fig.3,we assumed the ionization energy of ?E+EG=7.5 eV. When the ionization energy is decreased even to 5.5 eV, the fitting parameterEGincreases by only 0.1 eV.
The observedEGcan be interpreted by knowing the electronic structure of TiO2shown in Fig.4(a). The bandgap energy between the valence band top and the conduction bottom of anatase TiO2is 3.2 eV.[57,68]As the ionization energy,[57,68]defined as the energy of the vacuum level from the valence band top,we assume 7.5 eV as reported by Toyodaet al.[57]
TheEGof 3.6 eV obtained by fitting Eq. (11) to the NP B data in Fig. 3 disagrees with the established value of 3.2 eV.However, ourEG=3.6 eV for NP B is considered to correspond to the direct bandgap. Figure 4(b) schematically shows the band structure calculated by Daudeet al.[69]According to their calculation, both the top of the valence band and the bottom of the conduction band are at theΓpoint in the Brillouin zone, but the transition between these levels is forbidden. The bandgap energy of 3.2 eV observed by many groups is the energy of the “indirect transition” between theΓandXpoints. The allowed “direct transition” is at theXpoint. Reported direct bandgap energies range from 3.5 eV to 3.8 eV.[57,61,64,65,70]Our value agrees with the value calculated by Daudeet al.[69]
Next, we discuss theEG= 5.7 eV obtained by fitting Eq. (11) to NP A. Vos[71]reported that the conduction band of TiO2comprises two groups; the lower group is the tripledegenerated 2t2gstate and the upper group is the doubly degenerated 3egstate as shown in Fig. 4(a). The energy separation of the t2gand egstates was measured as 2.1 eV by Fisher[72]estimated from the x-ray absorption spectrum. Our observed state atEG=5.7 eV above the valence band top is considered to correspond to the transition from O2p to the Ti3d egstate.
In fact, an excited state close toEG=5.7 eV was observed by Argondizzoet al.[73]They observed several times enhancement of the photoemission for a 3.66 eV laser than at 3.22 eV and 3.95 eV.They irradiated a single crystal of rutile TiO2(111) with 20-fs laser pulses. They explained that the defect states lying 0.85 eV below the Fermi level were twophoton ionized. They also explained that the 3.66-eV light was in resonance with the transition from the defect states to the egstate as indicated by the thick red arrow in Fig. 4(a).The bandgap energy of rutile TiO2is 3.0 V.Therefore,assuming that the Fermi level is very close to the conduction band bottom,the energy of the egstate from the valence band top is 5.81 eV(=3+3.66?0.85)in their experiment for the crystal,and close to our observed value for NPs. Daudeet al.[69]reported the detailed band structure of TiO2. According to their calculation as schematically shown in Fig.4(b),the direct transition between the Ti 3d 3egand O 2p 1tgstates takes place at theXpoint with the transition energy of 5.7 eV. This value agrees with our fitting parameter ofEG=5.7 eV for the NP A data in Fig.3.
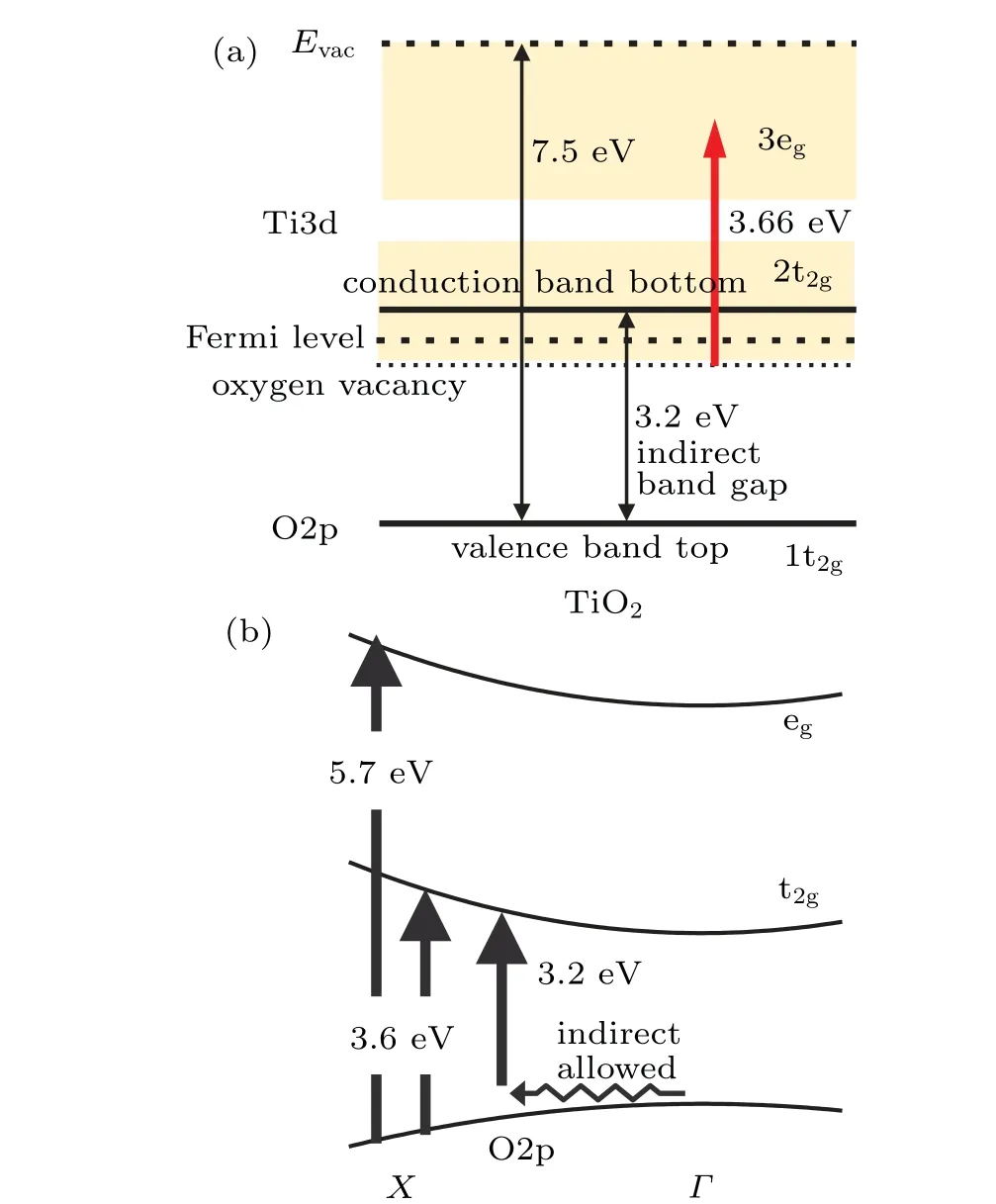
Fig.4. (a)Electronic structure of TiO2 obtained from references. The thick red arrow shows the transition to the eg level,which assists 2-photon ionization of the defect level lying below the Fermi level reported by Argondizzo et al.[73] (b)Schematic diagram of the band structure calculated by Daude et al.[69]
Thus,we confirmed that the value ofEGestimated by our theory is quite accurate. Readers should note that these values were estimated not from a single crystal but a single cluster of NPs.
We could attribute the difference between the 4-photon and 3-photon NPs to the difference in their defect densities.Thermionic electron emission is far easier from the high-lying egstate than from the low-lying t2gstate. We put concrete numbers. Whenhν= 1.77 eV,E0in Eq. (11) is 1.38 eV for 4-photon excitation to theEG=5.7 eV state and 1.71 eV for 3-photon excitation to theEG=3.6 eV state. When the ionization energy is 7.5 eV, ?Eis 1.8 eV and 3.9 eV for theEG=5.7 eV state and theEG=3.6 eV state, respectively.Then, exp(?4.5?E/E0) is 2.8×10?3for theEG= 5.7 eV state and 3.5×10?5for theEG= 3.6 eV state. However,four-photon excitation occurs with a very low probability than that of three-photon excitation. Bisioet al.[49]and Banfiet al.[50]observed a replica of energy spectra for two-photon and three-photon excitations of Cu(001)and Ag(100),respectively, which is the evidence of above-threshold photoemission. The intensity of the 3-photon excited Fermi edge was four orders of magnitude weaker than that of the 2-photon excited Fermi level. Therefore, thermionic emission from the low-lying t2gstate, which requires only 3 photons, is more probable than from the high-lying egstate. However, if there is a high density of defects,they assist the four-photon excitation to the egstate as shown in Fig.5. Hence,we can interpret that 4-photon NPs have a high density of defects.In the case of Argondizzoet al.,[73]the egstate assisted the ionization of the defect states,but in our case,the defects assisted the excitation of valence electrons to the egstate.

Fig.5. Multiphoton excited electrons are instantly thermalized. The excess energy Ek above the excited state heats the electron gas, and electrons with kinetic energies above ?E at the tail of the Boltzmann distribution escape into the vacuum, providing the PEEM image. When applied to the photon energy dependence of the electron yield,the theory reveals the excited states.Four-photon excitation to the eg state is assisted by the defect states lying below the Fermi level.
Figure 5 summarizes what our theory revealed. The Ti3d egstate at 5.7 eV above the valence band top is 4-photon excited from O2p. The excited electrons are instantly thermalized and the electrons at the tail of the Boltzmann distribution escape into the vacuum. The excess energyEkheats the electron gas in the excited state. With increasing the photon energy,the excess energy increases,leading to a drastic increase in the electron yield.Four-photon excitation of the egstate can be assisted by the defect state below the Fermi level. Allowed direct transition from the O2p to the t2glevel at theXpoint was also revealed by fitting the theory to the data of 3-photon slope NPs.
We now discuss the thermalization of electrons in the excited state. According to previous works, electrons are thermalized in about 10 fs[74,75]far shorter than the pulse width of 150 fs in the present experiment. Furthermore, in previous papers reporting the energy spectra, all spectra were thermalized,[11,55,75,78]supporting our instant thermalization assumption. Instant thermalization requires strong electronelectron collisions and excitation of many electrons in one NP.Accordingly,the present diagnostic requires high-intensity femtosecond irradiation.

wherehIis the contribution of additional laser heating. Then,Nemit=Neexp(??E/kT) increases with a non-integer slope.The slope changes with power and can be as large as 10 as was observed in our experiment for Au NPs.[51]
The derived theory also explains the difficulty of observing higher-orderm-PPE whose reasons were discussed in Winkelmannet al.[41]To observe higher-orderm-PPE,higher irradiation is required because the electron yield decreases by about 10?4for every higher order. Then the temperature of the electron gas can be very high and thermal emission even from low lying states can be very large. This argument is valid when electrons are instantly thermalized, which can be realized in solids. In gases, molecular density is low, electrons in the excited states may not be thermalized,and higher-order multiphoton ionization can be detected.
Finally, we discuss the expected structure of excitation spectrum ofm-PPE over the whole photon energy. At the very high photon energy region, ?E
5. Summary
In summary,a theory of multiphoton photoemission was derived and the excited states in the conduction band of a single TiO2NP were revealed by applying the theory. In the theory,photo-excited hot electrons are instantly thermalized,the excess energy of exciting valence band electrons to the excited state heats the electrons in the excited state,and hot electrons in the high energy tail of the thermal distribution escape into the vacuum.
The theory was applied to the experimentally observed photon-energy dependence of the electron yield of TiO2NPs.In most of the NPs,the yield increased with a 4-photon slope with the remainder exhibiting a 3-photon slope. The electron yields at 700 nm and 790 nm differed by as large as four orders of magnitude in the 4-photon slope NPs, and by three orders of magnitude in the 3-photon slope NPs. The derived theory well reproduced the observed excitation spectrum. From the fitting parameters,the excitation energies of the excited states were estimated as 5.7 eV and 3.6 eV in 4-photon and 3-photon excited NPs,respectively.The excited states were respectively assigned as the egand t2gstates. The estimated values agreed with those of previous observations and with the values calculated by Daudeet al.[69]Four photon excitation of valence band electrons to the egstate is presumably assisted by the defect level below the Fermi level.
The success of reproducing the wavelength dependence of electron yield as large as four orders of magnitude proved that electrons in the excited states can be instantly thermalized leading to strong thermal emission from the levels below the vacuum level. This mechanism explains the non-integer slope ofm-PPE and the difficulty of observing higher orderm-PPE.
- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

