Mengyang Qu(屈孟楊) Bo Zhou(周波) and Chunlei Wang(王春雷)

1Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3School of Electronic Engineering,Chengdu Technological University,Chengdu 611730,China

4Zhangjiang Laboratory,Interdisplinary Research Center,Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shanghai 201210,China

Keywords: wetting,work of adhesion,contact angle,water

1. Introduction

The wettability of materials by liquid water is fundamental to physics,chemistry,biology,and nanotechnologies.[1–13]Over the recent decades, with the development of the computer simulation[14–17]and experimental technologies,[18,19]it is possible to obtain the atomic level pictures of the water structure and hydrogen bond network near the interfaces.Utilizing these technologies, it has been revealed that water structures may show appealing ordered structures depending on the surface morphology.[20–23]Based on molecular dynamics (MD) simulations, we have predicted that water droplets coexist with the ordered water monolayer at room temperature on model surfaces, which can be termed an “ordered water monolayer that does not completely wet water”.[24,25]Similar phenomena has also been observed on surfaces of metals(such as Pd, Pt, and Al),[26–28]oxides (such as Al2O3and SiO2),[29]and talc.[30]Although the hydrogen bond number saturation of the water molecules within the water monolayer can explain this phenomenon,whether the Young equation still holds under this unconventional wetting framework is still not answered.

From the macroscopic standpoint, the contact angle formed by a water droplet on surfaces is the manifestation of the interaction between water and surfaces. The force balance discussed by Young to describe the shape of a droplet in equilibrium on a given surface takes the following form:[31]

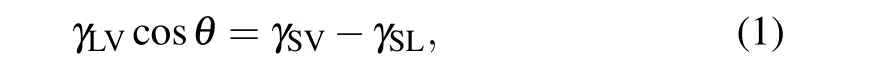
whereθis the contact angle,γLVis the liquid-vapor surface tension,γSLis the solid–liquid interfacial tension, andγSVis the solid–vapor surface tension. The wetting behavior of a given solid–liquid system may also be quantified through the work of adhesionWadh, which is defined by the work of reversibly removing a given liquid in equilibrium with its vapor from a given solid through

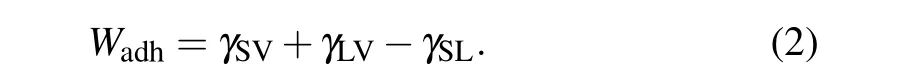
The combination of Eqs.(2)and(1)yields the Young–Dupr′e equation that connects the contact angle and the work of adhesion:

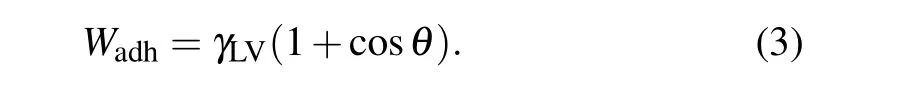
Equation(3)shows a linear relationship betweenWadhand the cosine value ofθunder conditions whereγLVremains constant, indicating that the wetability of surfaces can be quantitatively predicted by the value ofWadh. By definition,Wadhequals the change in free energy per unit area during the reversible removal process, which can be accessed by calculation of the free energy through the phantom-wall[32–34]and dry-surface methods.[35–38]

In this study, using an extended phantom-wall approach,we have calculated theWadhbetween liquid water and ordered water monolayer on different solid surfaces. For each interface,there is a linear relationship betweenWadhand the cosine values of the contact angle of droplets formed on the ordered water monolayer,which can be well fitted by Eq.(3). The results show that the Young–Dupr′e equation is also applicable for the interface of liquid water and ordered water monolayer,which gives a quantitative description of the unexpected phenomenon of “water that does not wet a water monolayer” at room temperature.

2. Methods

Three types of model surfaces were employed in this study. The first two types of model surfaces have a planar hexagonal structure of neighboring bond lengths of 0.142 nm consistent with that in Ref. [25]. We will refer to these types of surfaces as Hexa surfaces. For the type-1 Hexa surfaces, the Lennard–Jones parameters of atoms were set asσ= 0.3343 nm andε= 0.4393 kJ/mol. Positive and negative charges of the same magnitudeqwere assigned to the atoms located diagonally in neighboring hexagons as shown in Fig. 1(a). Hexa surfaces with different charges,q=1.0 e for Hexa-1,q=0.8 e for Hexa-2 andq=0.6 e for Hexa-3,were used, as shown in Table 1. As for the type-2 Hexa surfaces,the atoms were set as uncharged as shown in Fig.1(b),and the Lennard–Jones parameters of the atoms were set asσ= 0.3549 nm andε= 0.1595 kJ/mol for Hexa-4,ε=0.2363 kJ/mol for Hexa-5 andε=0.3426 kJ/mol for Hexa-6,as shown in Table 1. The type-3 model surfaces have a Fcc lattice with the (100) plane exposed to the liquid as shown in Fig. 1(c). We will refer to this type of surfaces as Fcc surfaces. The atoms of the Fcc-surface were modeled as uncharged Lennard–Jones particles,and the lattice constants and Lennard–Jones parameters are shown in Table 2.

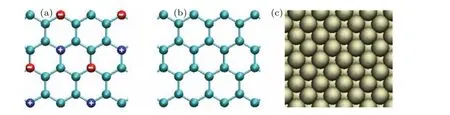
Fig. 1. (a) Geometry of the type-1 surfaces. Blue and red spheres represent the atoms of the solid with positive and negative charges,respectively, while the cyan spheres represent neutral solid atoms. (b) Geometry of the type-2 surfaces. The atoms of the solid were set as uncharged. (c)Geometry of the type-3 surfaces.

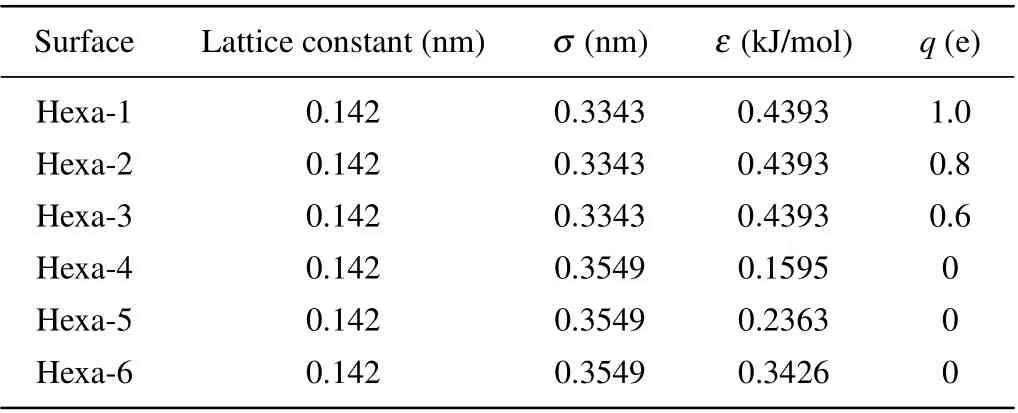
Table 1. List of the lattice constants and Lennard–Jones parameters of Hexa surfaces.

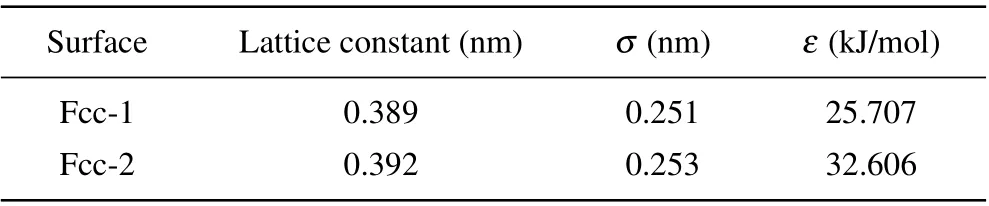
Table 2. List of the lattice constants and Lennard–Jones parameters of Fcc surfaces.

For each surface,we performed two series of simulations.To calculate the contact angles of water droplets,we employed cylindrical droplet equilibrium systems to avoid the line tension problem.[34,39]Initially, the size of surfaces were set as 3.44 nm×10.22 nm for Hexa surfaces,3.89 nm×11.67 nm for Fcc-1,and 3.92 nm×11.76 nm for Fcc-2 with a rectangle water droplet containing 2000 water molecules on the surfaces.The periodic boundary conditions were set in thexandydirections and the mirror boundary condition was employed in thezdirection. The height of the simulation box was set to 20 nm. To calculate theWadh, the sizes of surfaces were set as 3.44 nm×3.41 nm for Hexa surfaces, 3.89 nm×3.89 nm for Fcc-1,and 3.92 nm×3.92 nm for Fcc-2,with a water film thickness of about 10 nm next to the surfaces. Periodic boundary conditions were applied in all directions and the height of the simulation box was set to 50 nm.

The MD simulations were performed at constant volume and constant temperature(NVT)using the Gromacs 5.0.7 package.[40]The temperature was maintained at 300 K by Vrescale method with a coupling coefficient of 0.1 ps. All of the surface structures were kept fixed during the simulation.The rigid extended simple point charge (SPC/E) model[41]was used to describe the water molecules. The particle-mesh Ewald method[42]with a real space cutoff of 1 nm was used to treat long-range electrostatic interactions and 1 nm cutoff was applied to the van der Waals interactions. Specifically, our model specified a hydrogen bond between water molecules if the O–O distance was less than 3.5 °A and simultaneously the angle H–O...O was less than 30°.

3. Results and discussion

We have performed MD simulations to study the wetting behaviors of liquid water on different surfaces.Initially,a rectangle water droplet was placed on each surface. After 20-ns simulation, all of the systems for Hexa-1–3 and Fcc surfaces exhibit a cylindrical water droplet coexisting with the spread water monolayer on the surface, as shown in Figs. 2(a) and 2(b). This has been termed as room temperature“ordered water monolayer that does not completely wet water”. In contrast, there are cylindrical water droplets directly contacting with the surfaces in the systems of Hexa-4,Hexa-5,and Hexa-6 surfaces as shown in Fig.2(c).

To obtain the contact angles,the density distribution profiles of the droplets are firstly calculated. The regions with half bulk water density (0.45 g/cm3–0.55 g/cm3) are defined as the edges of the droplets. The edges are then fitted with circular shapes. The contact anglesθare measured from where the fitted circular arcs meet the water monolayer or surfaces.We determine the thickness of the water monolayer based on the water density profiles near the surfaces. The water density profiles as a function of the distance normal to the surfaces are shown in Fig.2(d),where profiles exhibiting prominent peaks,indicating the dense water monolayer near the surfaces. We thus determine the thickness of the water monolayer on different surfaces based on the location of the first valley of the density profiles, where the thicknessδ=0.4 nm for Fcc surfaces and Hexa-1,andδ=0.5 nm for Hexa-2 and Hexa-3.

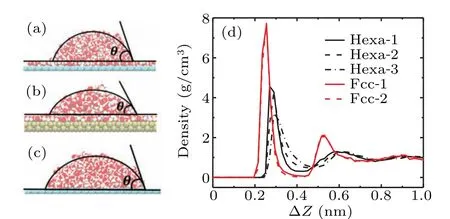
Fig.2.Side view of droplet coexist with the spread ordered water monolayer on (a) Hexa-1 to Hexa-3 and (b) Fcc surfaces. (c) Side view of droplet on Hexa-4 to Hexa-6 surfaces without the ordered water monolayer. (d)Water density distributions on Hexa-1 to Hexa-3 and Fcc surfaces, ?Z means the vertical distance to the surface.

Previous studies[24,25]attributed this unexpected phenomenon to the ordered structure of the water monolayer,which greatly enhances the numbers of H-bonds inside the monolayer and reduces the numbers of H-bonds between the water molecules inside the monolayer and other molecules.Thus,the fewer H-bonds number between the water molecules inside the monolayer and other molecules, the larger contact angles. Here,we have calculated the hydrogen bonds number between the water molecules inside the monolayer and other molecules. Here, the contact angle of the water droplets is inconsistent with the number of H-bonds between the monolayer and the droplet. As shown in Fig. 3, the number of Hbond per water molecule in the monolayer formed with the water molecules in the droplet on Fcc-1 and Fcc-2 surfaces are lower than that on Hexa-1 surface, nevertheless, the contact angle of droplet on Hexa-1 surface is larger than that on Fcc-1 and Fcc-2 surfaces.

Fig.3. Cosine values of contact angles θ of droplets versus H-bond numbers per water molecule in the monolayer formed with the water molecules in the droplet on Hexa-1 to Hexa-3 and Fcc-1 to Fcc-2 surfaces.

Fig.4. Schematic representation of the phantom-wall method.

We then calculate the work of adhesionWadhby employing an extended phantom-wall method. Details of the phantom-wall method can be found in the previous works[32,34]and are only briefly described here. In the phantom-wall method,a phantom-wall,which only has repulsive interactions with the water molecules is progressively displaced in the direction normal to the surface,while there is no interaction between the phantom wall and surface atoms. To control the position of the phantom-wall,a harmonic spring is attached in the direction normal to the surface, between each phantom-wall and the bottom of the simulation box. At the beginning, the phantom wall is controlled below the surface,where it cannot interact with water molecules since the distance between it and the water molecules is beyond the cutoff distance of the repulsive potential. The phantom wall is then slowly pushed up, by increasing the equilibrium length of the harmonic spring, such that it brings water molecules beyond the range of interaction of the surface, as shown in Fig. 4. The free-energy difference between the initial and final states,which equals to adhesion workWadhbetween water and the surface, can be calculated by numerically integrating the spring force over the equilibrium spring length along a reversible path.

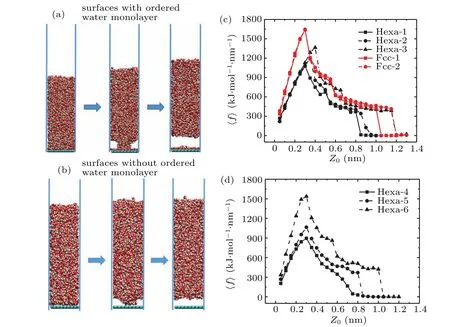
Fig.5. Snapshots of steps to separate the liquid water away from the surfaces(a)with and(b)without ordered water monolayer by increasing the equilibrium spring length in the extended phantom-wall method. The calculated spring force〈f〉as a function of the increased equilibrium spring length Z0 for surfaces(c)with and(d)without ordered water monolayer.

However,this approach cannot be applied to calculate theWadhbetween liquid water and ordered water monolayer,since the water monolayer may also be brought away from the surface by the phantom-wall. We have extended the phantomwall method to calculate theWadhbetween liquid water and ordered water monolayer. In the extended method,we directly control the position of the mass center of the water by attaching a harmonic spring between the mass center and the bottom of the simulation box using the pull code of Gromacs 5.0.7 package,[40]instead of utilizing a phantom-wall. The equilibrium length of the harmonic spring is increased step by step,as a result, the water molecules above the water monolayer was gradually separated from the surface, while the water monolayer remained on the surface due to the strong interaction between the first adsorbed water monolayer and surfaces. Each step is equilibrated for 8 ns to get the reversible path. Therefore, the free-energy difference between the initial and final states in this process exactly equals to theWadhbetween liquid water and the water monolayer.The simulation conditions and interaction parameters of the Hexa-4 to Hexa-6 surfaces and water molecules were set consistent with those in Ref. [37].TheWadhcalculated by the extended phantom-wall method is 50.234 mJ/m2for Hexa-4, 67.345 mJ/m2for Hexa-5, and 82.645 mJ/m2for Hexa-6,respectively,which is very close to the results,53 mJ/m2,63 mJ/m2,85 mJ/m2using dry-surface approach provided in Ref.[37],thus proved the correctness of the extended phantom-wall method.

To give a quantitative description of this unexpected wetting phenomenon of “ordered water monolayer that does not completely wet water” at room temperature, we have calculated theWadhof interfaces with or without ordered water monolayer by the extended phantom-wall method.We took 25 steps for each surface to separate the liquid water away from the monolayer or surfaces, increasing the equilibrium spring length every 0.05 nm. Each step is equilibrated for 8 ns. Snapshots of steps on separating the liquid water away from the monolayer are shown in Fig.5(a).As we can see,for interfaces with ordered water monolayer(Hexa-1 to Hexa-3 and Fcc surfaces)the liquid water was firstly partly separated and finally separated from the surfaces by the harmonic spring,while the position of the ordered water monolayer keeps unchanged due to the strong interaction between the surfaces and the monolayer. Different from Hexa-1 to Hexa-3 and Fcc surfaces, for the interfaces without ordered water monolayer (Hexa-4 to Hexa-6 surfaces), all of the water molecules above the surface, even the first adsorbed water layer was separated from the surfaces due to the weak interactions between the surfaces and water molecules above the surfaces as shown in Fig.5(b).TheWadhwas calculated by numerically integrating the spring force(f)over the increased equilibrium spring length(Z0)

where the〈···〉stands for a statistical average. The calculated〈f〉as a function ofZ0was shown in Figs.5(c)and 5(d). All of the spring forces increase first but then decreased and reach to zero finally, indicating the completely separating of liquid water from the monolayer or surfaces without any interaction.

Figure 6 plots the cosine values of contact anglesθ versustheWadhfor both interfaces with or without ordered water monolayer. There is a linear relation between theWadhand the cosine values of contact angles, which can be well fitted by Young–Dupr′e equation as Eq. (3). Here, we adopt the value ofγLV≈60 mJ/m2for SPC/E water model given by Vegaet al.[43]This means that the Young–Dupr′e equation holds for interfaces with or without ordered water monolayer. TheWadhbetween liquid water and ordered water monolayer can quantitatively predict the wettability of the ordered water monolayer even on different types of surfaces,consistent with the solid–liquid interfaces. These results give a quantitative description of the unexpected phenomenon of “ordered water monolayer that does not completely wet water”.

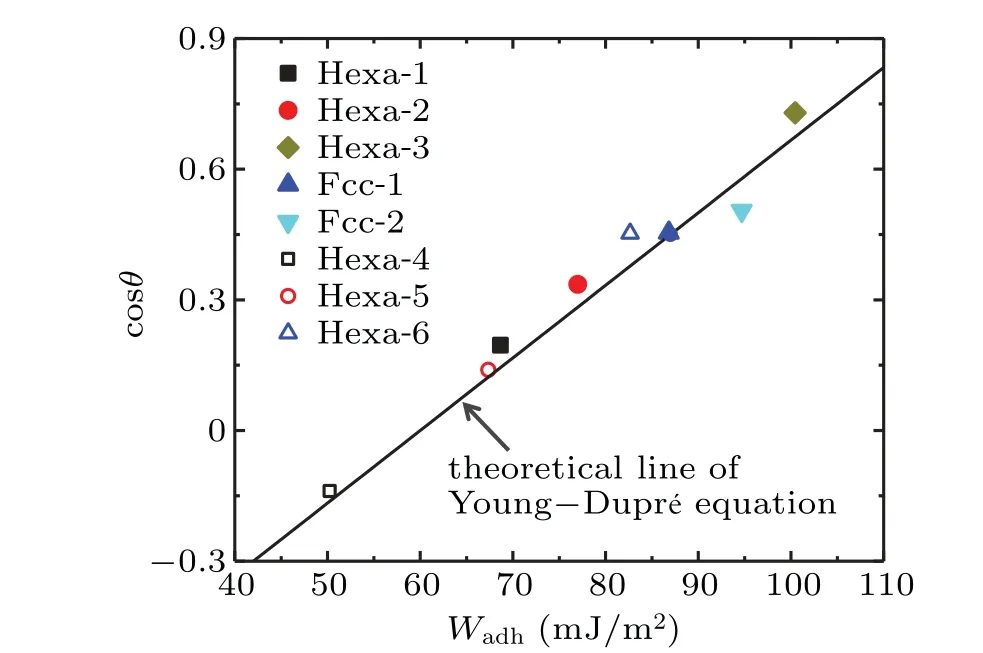
Fig. 6. Cosine values of contact angles θ of droplets versus the work of adhesion Wadh for interfaces with or without ordered water monolayer.

4. Conclusions

Based on an extended phantom-wall method,we have calculated the work of adhesion for interfaces with or without ordered water monolayer. The results show that the Young–Dupr′e equation holds on the solid surface with the ordered water monolayer, and give a quantitative description of the unexpected phenomenon of “ordered water monolayer that does not completely wet water” at room temperature. This study indicates that we should treat the water monolayer as part of the solid surface when we consider the Young equation in those novel wetting systems. The present study deepens the physical mechanism behind the wetting behavior, which would have implications in the actual fabrication of novel material for water treatment, surface catalysis and self-cleaning of surfaces.[44,45]

Acknowledgment

The MD simulations were performed with the Deepcomp7000 and ScGrid of the Supercomputing Center, the Computer Network Information Center of the Chinese Academy of Sciences,and the Shanghai Supercomputer Center of China.