SU Ke(蘇珂),WANG Chen(王晨),LIN Yumeng(林雨萌)

(1.College of Mathematics and Information Science,Hebei University,Baoding 071002,China;2.Hebei Province Key Laboratory of Machine Learning and Computational Intelligence,Baoding 071002,China)

Abstract:In this paper,we mainly study the dual problem of the nonconvex semi-infinite programming problem with inequality constraints.It is well known that there is usually a duality gap in constructing duality problem using the ordinary Lagrangian function.To eliminate the duality gap,we construct an augmented Lagrangian function,then discuss its duality.Under reasonable assumptions,the strong duality theorem between the primal problem and the augmented Lagrangian dual problem holds.Finally,an example is given to verify the presented results.

Key words:Semi-infinite programming;Nonconvex;Duality;Augmented Lagrangian function

1.Introduction

Semi-infinite programming,which contains a finite number of variablesx=(x1,··· ,xn)∈Rnon a feasible set and an infinite number of constraints,is a common optimization problem.Semi-infinite programming can be used in Chebyshev approximation[1],optimal control and transportation problem[2].It also can be found in molecular biotechnology,such as finding optimized complex control strategy in some special control system[3].

In the article,we consider the augmented Lagrangian dual problem of nonconvex semiinfinite programming with inequality constraints.For convex semi-infinite programming,there are many literatures[4?6]have discussed it’s duality theory and optimal solution properties.A primal-dual augmented Lagrangian method for solving an equality constrained minimization problem was considered by Armand[7].For convex programming with finite number of constraints,theoretical properties of the augmented Lagrangian duality were systematically analysed by using the conjugate duality theory in[8].In general form,the idea of constructing augmented Lagrangian functions was presented by Rockafellar and Wets[9].Similarly,in an infinite dimensional setting,Azimov[10]constructed a sharp augmented Lagrangian function to obtain some strong duality results.For solving constrained nonconvex optimization problem,a new sharp augmented Lagrangian-based global optimization method[11]was presented.

Most of the existing literatures are based on Lagrangian function to obtain the dual problem of constrained programming,while the augmented Lagrangian function is less used to study the dual problem.Motivated and inspired by the research of semi-infinite programming duality theory,in this paper,we construct an augmented Lagrangian function,then we give sufficient conditions for the strong duality of nonconvex semi-infinite programming.

The structure of this paper is as follows.In Section 2,we introduce some basic knowledge and constructed augmented lagrangian function.In Section 3,we discuss the duality between the primal problem and the dual problem and give an example.We give a conclusion in Section 4.

2.Preliminaries

3.Duality

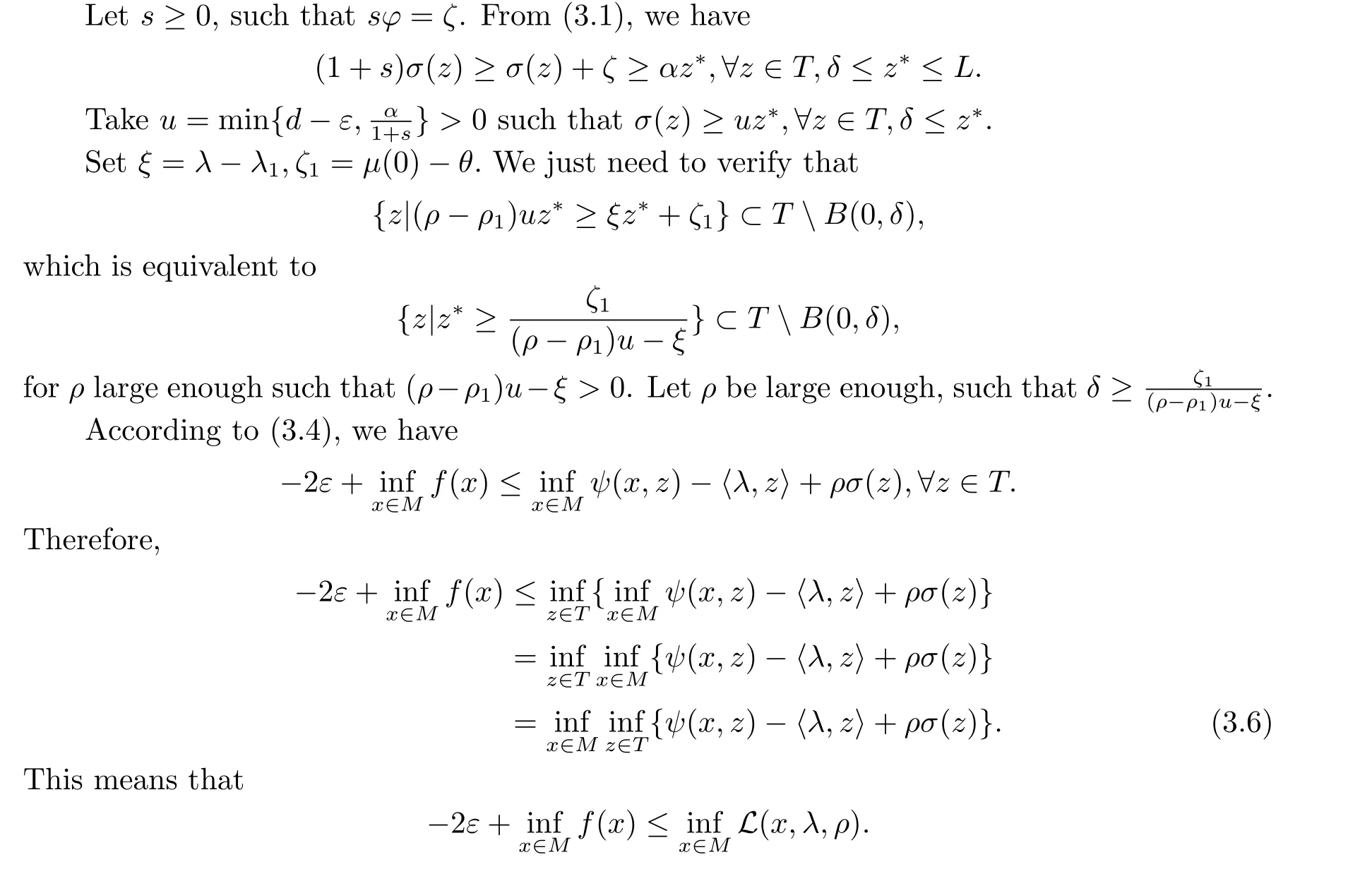
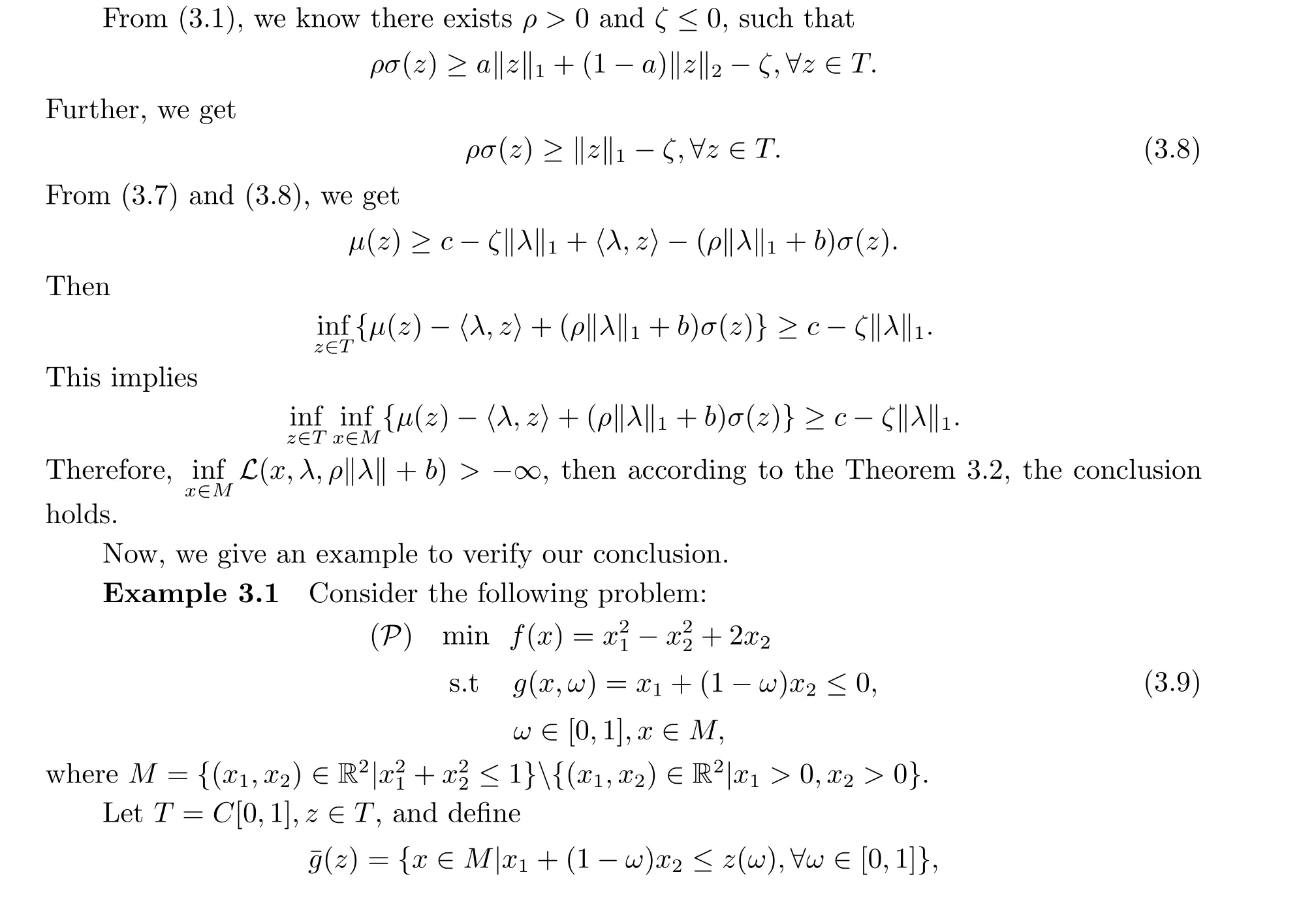
4.Conclusion

Duality theory has the most profound influence on semi-infinite programming.However,there is usually a duality gap between primal problem and its dual problem by the standard Lagrangian function.Therefore,in this paper,the augmented Lagrangian function is constructed for nonconvex semi-infinite programming and its dual problem is systematically discussed.Under the suitable conditions,the strong duality holds,that is,there is no duality gap.This method is a generalization of the existing method.