Plasticity and melting characteristics of metal Al with Ti-cluster under shock loading*
Dong-Lin Luan(欒棟林) Ya-Bin Wang(王亞斌) Guo-Meng Li(李果蒙)Lei Yuan(袁磊) and Jun Chen(陳軍)
1School of Mechatronic Engineering,Beijing Institute of Technology,Beijing 100081,China
2System Engineering Research Institute,Beijing 100094,China
3Beijing Special Vehicle Research Institute,Beijing 100072,China
4Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
5Center for Applied Physics and Technology,Peking University,Beijing 100871,China
Keywords: molecular dynamics,impurity cluster,dislocation,shock loading
1. Introduction
Impurity always is an important issue in the area of metal property study. Owing to the uneven distribution of the components, the properties at the location where the impurities gather are quite different from in other regions,which will affect the overall performance of material.[1,2]Metal Al has been widely used in aerospace, construction, military and other fields, and Al is often used by adding Ti to improve its mechanical performance. As a consequence, the aggregation of impurity Ti l inevitably occurs in Al.[3-5]The studying of influence of Ti aggregation is of great significance in putting metal Al into practical applications.
Previous studies have discovered that impurities can affect response mechanism of metal material under shock loading. Rigget al. conducted the shock loading experiment on Zr with three different densities of impurities. The results showed that for both ramp and shock loading,the phase transition stress of Zr increased with the density of impurities increasing.[6]Asay and Gupta tested the influence of impurity density on the attenuation of the elastic precursor decay.It was concluded that the rate of attenuation of high-amplitude elastic waves is reduced for a given defect concentration if the defects are clustered.[7]Regional segregation was also a typical form of impurity concentration.[8]When the molten pool crystallizes, the impurities will be“driven” toward the center of the molten pool,making the center of the molten pool have more impurities than other regions. The microstructure and mechanical properties proved to be directly related to microsegregation. Zouet al. found that the aggregation of Au can promote the generation of internal dislocations by studying the phenomenon of surface segregation.[9]Jovanaet al.conducted a research on the Mo segregation phenomenon of Ti-Mo alloy. Their results showed that in the Mo-rich area,the values of corresponding hardness and elastic modulus are lower than in other area.[10]Hippsleyet al.studied the stress-relief cracking of Cr-Mo alloy and found that the segregation is harmful to the material properties. Under low stress strength, it can promote cracks to propagate through the spacing between granules.[11,12]The radiation-induced segregation of binary alloys was studied by Okamoto and Rehn. Their results show that the radiation-induced segregation has a negative effect on the phase stability.[13]Koike and Mabuchi observed the segregation of solute elements at the interface and grain boundaries,and concluded that this segregation is the key reason for melting along the interface and grain boundaries.[14]Chenet al.[15]and Viswanadhamet al.[16]found that the segregation of Mg and other metals at the grain boundary in the Al-Zn-Mg alloy can result in stress corrosion cracking. In the study of Nb-40Ti-15Al alloy, it was found that Cr element has severe intragranular segregation and this intragranular segregation can cause the intergranular fracture to form.[17]
Non-equilibrium molecular dynamics (NEMD) is an available method to analyze the shock response micromechanism on an atomic scale. Kadauet al.used this method to study the behavior of iron under shock loading, and discovered the nucleation in the crystal when the impact strength exceeds the plastic deformation threshold.[18]Mintmireet al.explored the phenomenon of hot spots’formation induced by atomic-scale holes.[19]Liet al. simulated the response process of porous magnesium under shock loading,and explored the dominant mechanism of hole collapse and the effect of holes on shock wave propagation.[20]Liaoet al.also used the NEMD to probe the relationship between the energy dissipation and porosity of gradient porous nickel and the mechanism relating to pore collapse.[21]
In this paper, the non-equilibrium molecular dynamics method is used to investigate the micro mechanism of impurity Ti in metal Al under shock loading. Two models,i.e.,Ti-cluster model and perfect Al model,are built and compared with each other to understand the mechanism of impurity effect. The Hugoniot curves are calculated and compared with the experiment results. The atomic strain, pressure, and temperature field are calculated. The mechanism of the dislocations caused by Ti clusters is explored. Our results show that Ti clusters have a great influence on the formation of dislocation and the distribution of temperature. The Ti-cluster gives rise to dislocation distribution in the shape of grid-like structure, and thus reducing the dislocation density. In terms of temperature distribution, the high-temperature regions of the Ti-cluster model are concentrated on the Ti cluster and the dislocation intersection.
The rest of this paper is organized as follows. The model and simulation methods are described in Section 2. The detailed simulation results and discussion are presented in Section 3.The conclusions drawn from the present study are summarized in Section 4.
2. Method
The large-scale atomic/molecular massively parallel simulator (LAMMPS) is used to simulate the process of nonequilibrium molecular dynamics.[22]The Al-Ti binary embedded atom method(EAM)potential is selected to express the interaction between the aluminum atoms and titanium atoms.[23]
For simplicity,the model of aluminum block with Ti clusters is used to describe the phenomenon of Ti impurity density,the size of the aluminum block is set to be 60×60×300×elementary cell(lattice constant of FCC Al isa=4.05 ?A),which contains about 4.7×106atoms. The 5 titanium clusters with a radius of 20 ?A are set to be in an interval of 200 ?A in order to explore the influence of Ti segregation(see Fig.1(a)for details). In addition, the same size model of pure aluminum block is assumed as a control group as shown in Fig.1(b).
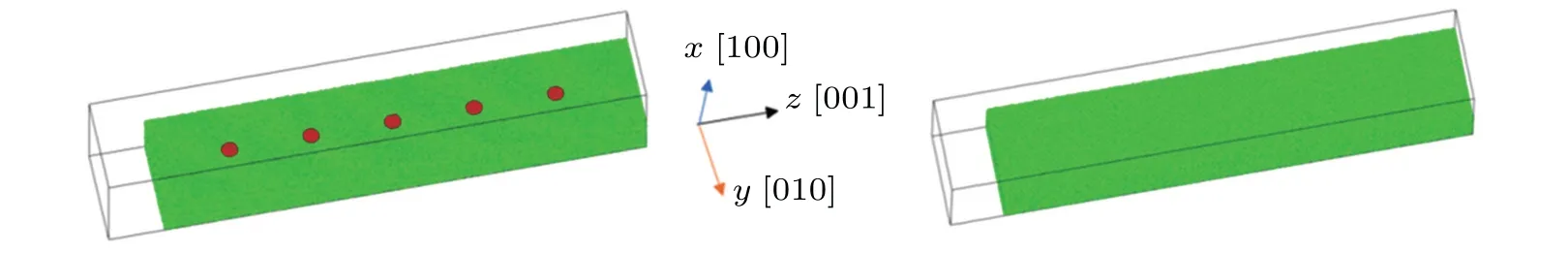
Fig.1. Simulation models: (a)Ti-cluster model and(b)perfect Al model,where green part represents Al atoms,and the red solid circle denotes Ti atom.
A piston model is used to simulate the formation of shock waves. The size of the piston is 60 elementary cells×60 elementary cells×30× elementary cells, and the piston impacts along thez-axis direction at a constant shock velocity of 750 m/s, 1000 m/s, 1250 m/s, 1500 m/s, 1750 m/s, separately. And the simulation time step is set to be 0.2 fs to ensure numerical stability. Each model needs to use the conjugate gradient method to minimize the system energy before the shock loading,which means that the system atoms are relaxed for 40 ps, leading the system environment to enter an equilibrium state under the conditions of 300 K and 0 GPa in the constant-pressure and constant-temperature(NPT)ensemble environment. This numerical simulation technology has been widely used in molecular dynamics simulation of shock loading.[24-27]
The visualization software OVITO[28]is used to visualize and process the data obtained from the simulation. The common neighbor analysis (CNA) is adopted to identify changes in the lattice structure.[29]The dislocation extraction algorithm(DXA)[30]is used to identify the dislocations that occur in the model.In addition,in order to obtain the local thermodynamic information of the model,binning analysis is also used to calculate the local pressure and temperature, and to obtain the wave profiles.
3. Results and discussion
3.1. Hugoniot curve of Al
The multi-scale shock technology(MSST)is used to calculate the shock Hugoniot curves of Al. The MSST method combines molecular dynamics and Euler equations to achieve compressible flow and can perform molecular dynamics simulation of the system under dynamic shock conditions,and the method has the ability to for much longer time than NEMD method has.[31]Considering the fact that dozens of sets of simulations need to be performed under different shock velocities and a moderate change in size will not affect the reliability of the results,the size of the model is set to be 20 elementary cells×20 elementary cells×100 elementary cells to reduce the computation time, which contains about 2.0× 105atoms in total.Thex,y,andzdirections adopt periodic boundary conditions.The obtained data are used to draw Hugoniot curves and compared with the previous experimental results,[32]which are shown in Fig.2(a).
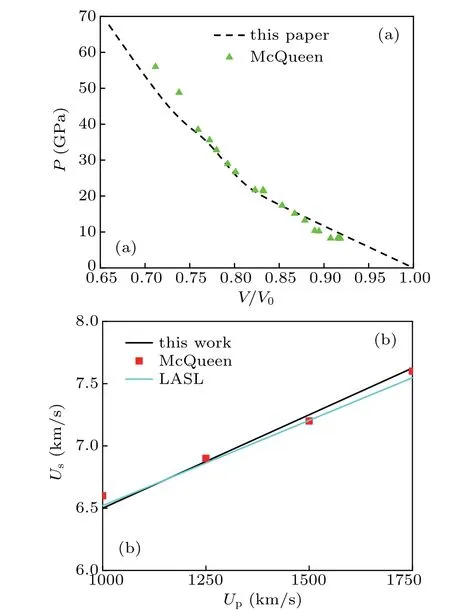
Fig. 2. (a) Comparisons of Hugoniot curves between MD simulations and experimental results. (b)Shock wave velocity(Us)-Piston velocity(Up)relationship.
Figure 2(a) shows that when pressure is lower than 40 GPa, the simulation results by using the potential function are basically consistent with the McQueen’s results;when pressure is higher than 40 GPa,there is a certain deviation between the simulation results and experimental results,and the deviation is about 6%. It can be seen that the current EAM potential is more suitable for pressures below 40 GPa. For this reason, the shock pressure we used in the follow-up simulations is below 40 GPa. Within this pressure range,the simulation results are well consistent with the experimental results.
In order to further confirm the reliability of the result of the potential function, the relationship between the shock loading velocity(Up)and the shock wave velocity(Us)is obtained,and the results are compared with the experimental data obtained by McQueenet al.[32]and the results recorded by Marsh[33]as shown in Fig. 2(b). The simulation results obtained by using this potential function[23]conform to the linear relationship ofUs=C0+λ·Up,whereC0is a parameter similar to the bulk sound velocity andλis a coefficient. According to Fig.2(b),the simulation parameters are well consistent with the experiment data. Marsh showed thatC0=5.15 km/s andλ= 1.37, and the result of the MD simulations showsC0=5 km/s andλ=1.5,the deviation between them is below 10%. In the published studies,the EAM potential function has been widely used to describe the interaction between Al atom and Ti atom.[34-36]Through the previous discussion,this function can also accurately describe the interaction relationship between aluminum atoms. Therefore,the result calculated by this EAM potential is credible,which lays a foundation for the subsequent analysis of the effect of Ti impurities clusters on metal Al under shock loading.
3.2. Dislocation and strain distribution of models under shock loading
Dislocation is a typical phenomenon that occurs in alloy under shock loading. We have simulated the shock loading process of the two models at 5 different shock velocities. The DXA module in the OVITO is used to analyze the change of the crystal structure and dislocation distribution of the model,and the difference between the two models in these aspects is particularly clear at a shock velocity of 1000 m/s as shown in Fig.3.

Fig. 3. Dislocation distribution at 16 ps from (a) Ti-cluster model and (b)perfect Al model.
The dislocation distributions of the two models are shown in Fig. 3. Under a shock velocity of 1000 m/s, dislocations are formed by nucleation and then move along the slip surface{111}, forming two different dislocation distributions. Further, we summarize the dislocation density of the two models. The dislocation density from the Ticluster model is 2.15×10-3?A-2, and that from the perfect Al model is 2.18×10-3?A-2, but the dislocation density and dislocation distribution in local region are fairly different. Three regions are separated by the black dotted lines according to the results of dislocation distribution and marked as regions I, II, and III. In region I, the dislocations of the two models are basically the same without the effect of Ti clusters, and the dislocation density from the Ti-cluster model is 3.15×10-3?A-2, that from the perfect Al model is 3.06×10-3?A-2,a large number of dislocations and twins appear randomly along the{110}plane which is typical slip direction of FCC metal.In region II,the dislocation density from the Ti-cluster model is 2.35×10-3?A-2,that from the perfect Al model is 2.82×10-3?A-2. Compared with the perfect Al model,the Ti-cluster model has a low dislocation density,and the dislocations present a special grid-like structure. In region III,no plasticity occurs in the perfect Al model,however,the dislocations can still be observed in the Ti-cluster model. In order to investigate whether the difference in dislocation distribution between the two models is due to the influence of titanium clusters,the dislocation formation process at the cross section of the titanium cluster in chronological order is shown in Fig.4,and the green dots in Fig.4(a)represent the titanium clusters.
The relationship between the dislocation and the position of the titanium cluster can be clearly seen in Fig.4(a). Whent=10 ps,the shock wave reaches the third Ti cluster. The dislocations originate from the titanium clusters, and then grow along the slip surface as the impact time increases. Unlike the uniform distribution of dislocations in the perfect Al model,the titanium clusters have a concentrated effect on the distribution of dislocations,which can limit the dislocations to the slip plane passing through the titanium clusters,presenting a gridlike structure. Therefore,the influence of the titanium clusters can be regarded as the main reason for the different dislocation distributions of the two models. To analyze the role that the titanium clusters play in forming the dislocations,the local figures at the third titanium cluster under a shock velocity of 1000 m/s are displayed in Fig.5. Figures 5(a)-5(h)show the crystal structure transformation and the process of dislocation formation,and figures 5(i)-5(l)display the shear strain results at the Ti cluster based on the Atomic Strain of OVITO.

Fig.4. Dislocation formation process from(a)Ti-cluster model and(b)perfect Al model under shock velocity of 1000 m/s.
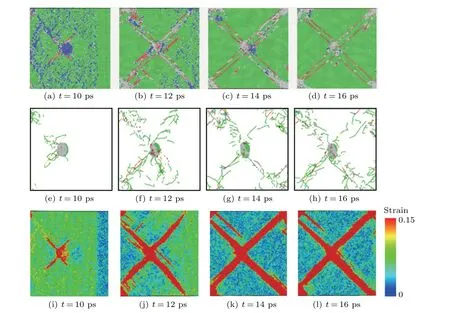
Fig.5. (a)-(d)Microstructure at Ti cluster,(e)-(h)process of dislocation formation at Ti cluster,and(i)-(l)time-dependent image of atomic strain at Ti cluster.
Under the shock loading, the high strength of titanium plays a dominant role in forming the special gird-like structure. Whent=10 ps,the shock wave front just reaches the Ti clusters due to the high strength of titanium,the shock wave is obviously hindered and compressed, and a visible high strain zone is formed in front of the titanium clusters as shown in Fig.5(i). According to the dislocation theory,the dislocations occur either from natural source of dislocations or by nucleation,and strain concentration is precisely one of the important reasons for nucleation.[37,38]In the absence of natural dislocation source in the model,the high strain zone formed near the titanium clusters creates conditions for dislocation nucleation.Since the dislocation nucleation energy in titanium is higher than that in aluminum,it is easier to nucleate in aluminum than in titanium. The location of the nucleation is on the aluminum side of the Ti-Al interface as shown in Fig. 5(a). After that,the shear strain in the direction of dislocation glide reaches its maximum value(about 0.5),dislocation moves along the slip direction,a cross-shaped dislocation is formed at the titanium cluster,and the dislocations at multiple titanium clusters form a grid-like structure as shown in Fig.4(a).
In addition to affecting the dislocation distribution by affecting the position of the nucleation, titanium clusters can also promote the dislocations to form to a certain extent, and the promoting the titanium clusters to affect dislocation formation is particularly obvious under low-velocity impact.Figure 6 shows the microstructural comparison between the two models at an impact velocity of 750 m/s. Under this shock velocity, the energy of the shock wave is not high enough to reach the activation energy of nucleation of Al, so, no plasticity occurs in the perfect Al model. However, due to the strain concentration in front of the Ti cluster,the uniform nucleation mechanism in the perfect Al model is transformed into the non-uniform nucleation mechanism in the Ti-cluster model,which greatly reduces the average stress of dislocation nucleation, making it easier for dislocation to occur. After the propagation of the shock wave is blocked by the titanium cluster, the shock wave pressure in the compression zone in front of the titanium cluster increases in the Ti-cluster model,and the shock wave energy reaches the critical value of nucleation. Subsequently,the dislocation climbing activation energy of dislocation glide is also satisfied,forming the dislocation distribution as shown in Fig.6(a).
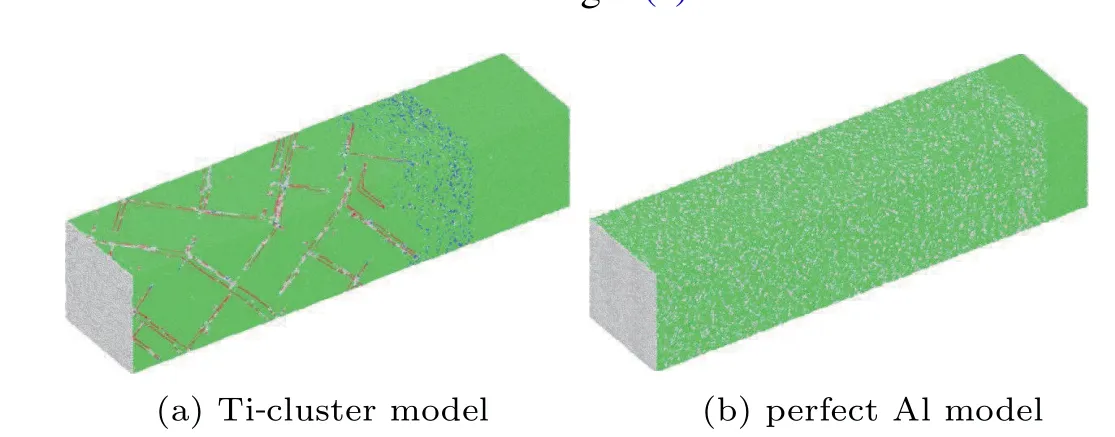
Fig.6. Microstructure of(a)Ti-cluster model and(b)perfect Al model under shock velocity 750 m/s.
However, the influence of the titanium clusters on dislocation formation is fairly related to the shock velocity. Under different shock velocities,the DXA analysis results of two models are shown in Fig.7.
A comparison among the results of Figs.3,6,and 7 shows that the degree of influence of titanium clusters is directly related to the shock velocity. The black box in Fig. 7 corresponds to the region where the difference in dislocation density between the two models is the largest in Fig. 3. When the shock velocity(SV)is 1250 m/s,the influence of titanium clusters on the dislocation distribution can still be seen,but it is not so obvious as that of the difference under a shock velocity of 1000 m/s. When the shock velocity is 1500 m/s,there is basically no difference between the two models,both showing a large area of disorder structure. According to the current results,when the shock velocity is lower than 1000 m/s,the energy of shock wave is not high enough to make the nucleation occur in the perfect Al model, yet dislocations are formed in the Ti-cluster model because of the strain concentration effect of Ti clusters as shown in Fig. 6. When the shock velocity is higher than 1000 m/s, due to the relatively low strength of aluminum,the impact energy reaches the sliding activation energy of aluminum, a wide range of dislocations consequently appear in the metal aluminum. Since the nucleation generally occurs in the model rather than is limited to the front of the titanium cluster,titanium clusters can no longer have a significant effect on the dislocation distribution. Therefore, it can be concluded that the effect of the local titanium clusters on the dislocation of the whole model gradually weakens as the shock velocity gradually increases.

Fig. 7. Microstructure of two models under different shock velocities(SV): (a) Ti-cluster model and SV=1250 m/s, (b) perfect Al model and SV=1250 m/s,(c)Ti-cluster model and SV=1500 m/s,and(d)perfect Al model and SV=1500 m/s.
In addition, the pressure data of the two models under different shock velocities are calculated to explore the influence of Ti cluster on the pressure during impact compression as shown in Fig.8. The results show that the Ti concentration phenomenon has no effect on the overall pressure propagation process, which is related to the size of the Ti clusters. The size of the clusters is only 1/12 of the width of the shock loading section,which is too small to have a significant impact on the overall pressure, and the influence of clusters size on the overall pressure needs further studying.
Figure 9 shows the lateral pressure analysis results of the two models at a shock velocity of 750 m/s and 1000 m/s. Although the Ti cluster has no obvious effect on the overall pressure during the shock loading,it can be observed that a significant pressure rise occurs in the middle of the model as indicated from the results of the transverse slice analysis,which is also the reason for the different dislocation distributions of the two models.
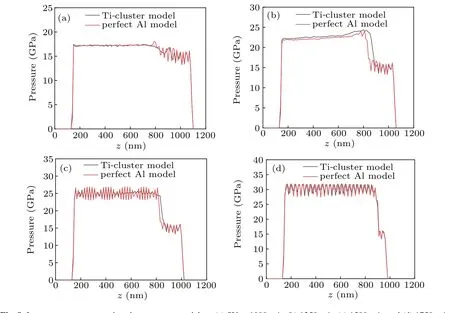
Fig.8. Impact pressure comparison between two models at(a)SV=1000 m/s,(b)1250 m/s,(c)1500 m/s,and(d)1750 m/s.
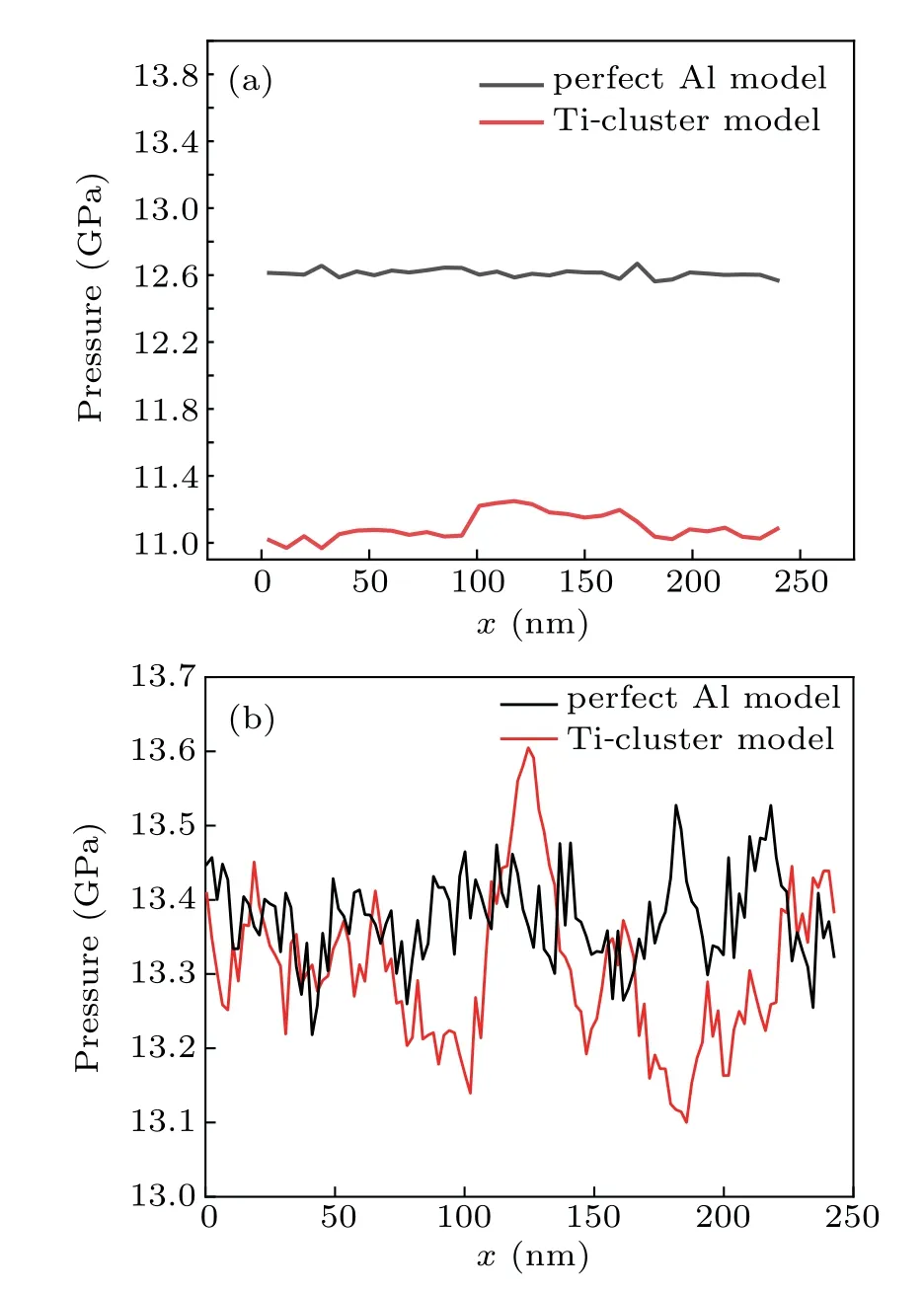
Fig. 9. Model transverse slice pressure analysis at SV=750 m/s (a)and 1000 m/s(b).
In summary, the concentration of Ti atoms in the metal Al can hinder the shock waves from propagating, and affect the dislocation distribution through strain concentration nucleation. And due to the strain concentration in front of the titanium cluster, it can promote the formation of dislocations at lower shock velocities(<1000 m/s).
3.3. Thermodynamic properties of models under shock loading
The thermodynamic characteristics of the two models under shock loading are calculated and analyzed,mainly including the formation and distribution of high-temperature region and the analysis of thermal effects at the dislocation intersection. To express the temperature distribution of the model,the neighbor region of each atom is divided, and the temperature of a single atom is defined as the average temperature of all atoms in the neighbor region and calculated by averaging kinetic energy of its neighbor atoms. Since the shock wave front has not yet reached the condition of equilibrium temperature,in order to avoid overestimation of temperature,the kinetic energy here only refers to the kinetic energy brought about by the velocity perpendicular to the direction of shock loading. This method is used in the calculation of local temperature in the field of molecular dynamics.
The temperature distributions of the two models at the shock velocity of 1000 m/s in chronological order are shown in Figs.10(a)and 10(b). The time sequence from top to bottom of each sub-picture is 4 ps,8 ps,12 ps,16 ps. An enlarged view of the local temperature near the Ti clusters is shown in Figs.10(c)-10(f).
As shown in Figs.10(a)and 10(b),the two models present two different temperature distributions at the same loading time. In the Ti-cluster model,hot spots are mainly distributed near the titanium clusters and the edge of the model, and the perfect Al model has no obvious regular pattern. Figures 10(c)-10(f)displays the local temperatures near the titanium cluster over time. This can be explained by the hot spot formation theory, and local heating caused by dislocations is one of the important reasons for the formation of hot spots.Based on the analysis in Subsection 3.2, under low-velocity(1000 m/s) impact, the strain concentration formed in front of the titanium cluster promotes the dislocations to nucleate,and the local heating at the dislocation causes the hot spots to form near the titanium clusters, when the dislocation moves outward along the{110}slip plane, a series of hot spots is formed, which is consistent with the hot spot formation process shown in Figs. 10(c)-10(f). In addition to the hot spots formed in front of the Ti clusters due to strain concentration,additional hot spots are also observed at the edge of the model.
In order to explain the reason for the high temperature area at the edge of the model, the temperature image is compared with the dislocation image as shown in Fig. 11. The temperature at the intersection of the dislocation at a shock velocity of 1000 m/s is about 600 K,locally reaching 650 K,yet the high temperature area of the perfect Al model is about 500 K. It can be found the hot spot distribution at the edge of the model is highly coincident with at the location of dislocation intersection in the Ti-cluster model. This shows that while the titanium cluster changes the dislocation distribution,the resulting temperature distribution is changed,and there is a significant temperature rise at the intersection of dislocations.Owing to the coincidence of the model size settings,when the dislocation moves outward along the{110}slip plane, it just intersects at the edge of the model,and the subsequent development of dislocations cannot be observed.
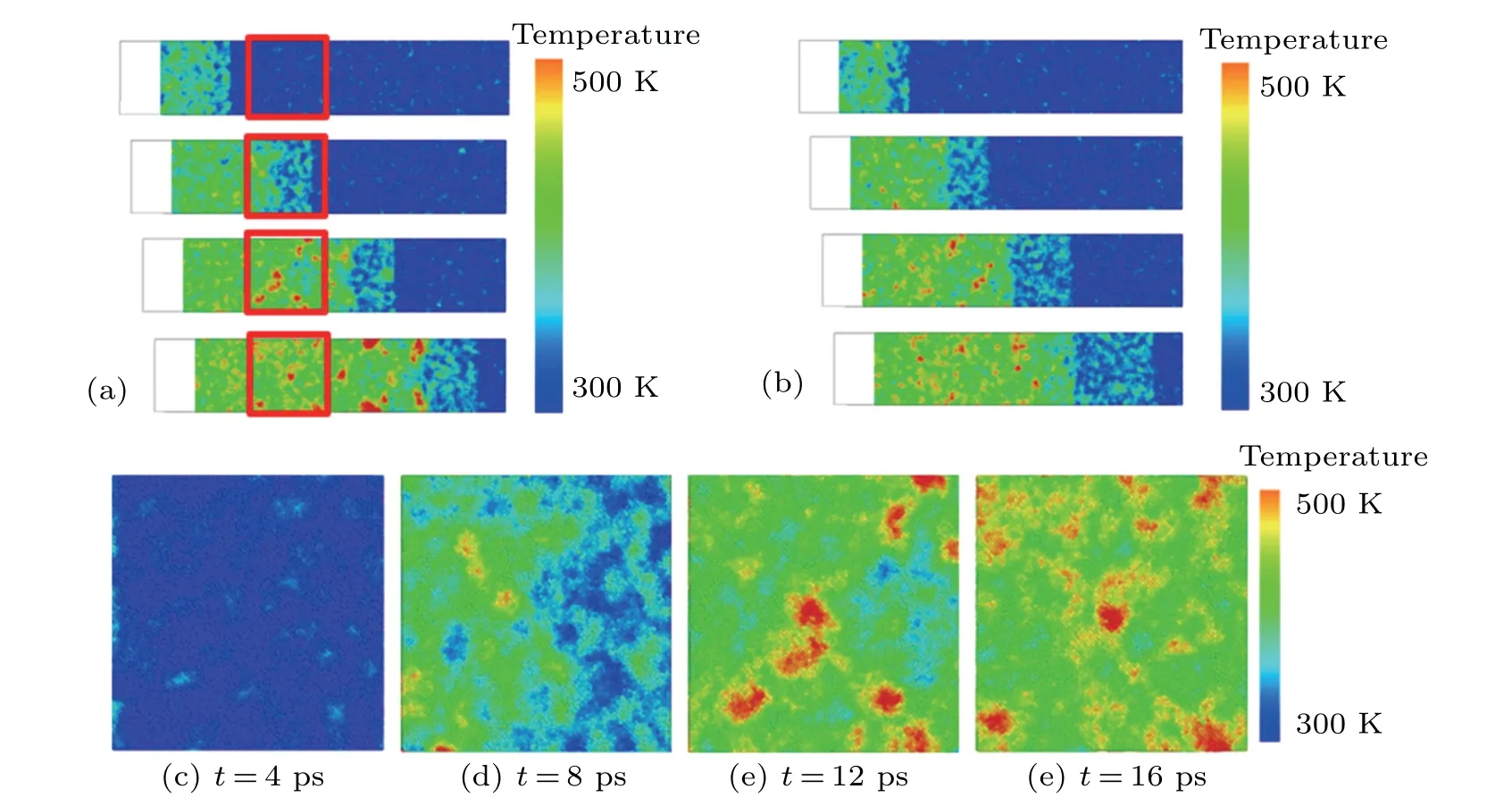
Fig.10. Temperatures varying with time from(a)Ti-cluster model,(b)perfect Al model,(c)-(f)enlarged view of local temperature near Ti clusters.
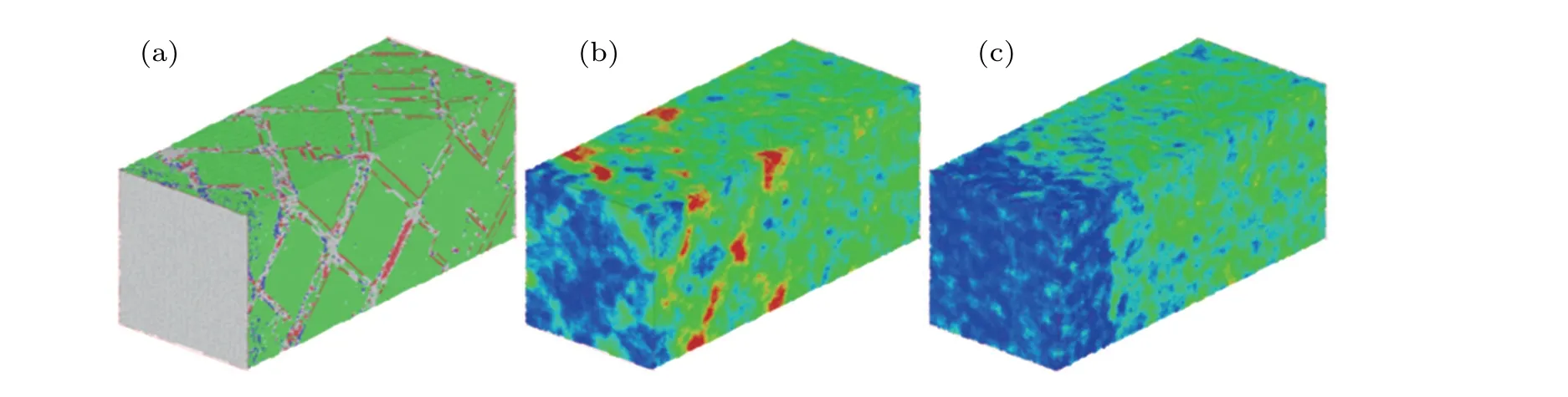
Fig.11. Link between dislocation intersection and hot spot in Ti-cluster model,showing(a)dislocation distribution,(b)local temperature of Ti-cluster model,(c)local temperature of perfect Al model.
To explore whether the influence of titanium clusters on the formation of hot spots is related to the shock velocity,the temperature comparison between the perfect Al model and the Ti-cluster model at the same time under different shock velocity are conducted as shown in Fig.12. According to the results of Fig.12,the temperature distributions of the two models are clearly different before the shock velocity reaches 1750 m/s.When the shock velocity is 1000 m/s,the temperature rise effect at the titanium cluster is more obvious than that from the perfect Al model, and the temperature at the titanium cluster is about 100-K higher than the adjacent area. As the shock velocity increases, the conditions required for nucleation are satisfied, and a large number of dislocation sources appear in both models. When the shock wave reaches the titanium cluster, it will still form a high temperature zone near the titanium cluster. However,owing to the high-speed impact,the microstructure undergoes major change. With a large number of dislocations occurring,the heat near the titanium cluster is rapidly conducted outwards,the temperature near the titanium cluster gradually tends to the nearby area, however, the temperature rise near the dislocation intersection point can still be observed.When the shock velocity reaches 1750 m/s,the local temperature at the front of the shock wave is close to the melting temperature of aluminum,and there is no much difference between the two models.
The effect of titanium clusters on temperature distribution under shock loading mainly includes the following iteams: titanium clusters hinder the shock waves from propagating and promote the hot spots to form near the titanium clusters and the dislocation sources to be generated. When the dislocation moves along the slip surface,a series of hot spots is generated,and there is a significant temperature increase at the position where the dislocations intersect. Owing to the high temperature at the dislocation intersection and near the Ti clusters,the partial melting of aluminum may be advanced with the shock velocity increases.
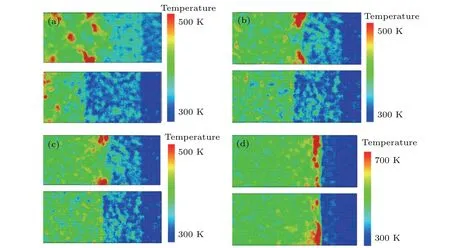
Fig.12. Comparison between temperatures of Ti-cluster model(upper)and perfect Al model(lower)with shock velocity SV=1000 m/s,(b)1250 m/s,(c)1500 m/s,and(d)1750 m/s.
4. Conclusions
In this paper,the non-equilibrium molecular dynamics is used to investigate the micro mechanism of impurity Ti in metal Al under shock loading, the dislocation formation and temperature distribution are analyzed on an atomic scale. The Hugoniot curve of Al is calculated and compared with the experiment results to verify the reliability of the EAM potential. Dislocation formation process, atomic strain, temperature, pressure, and other properties under shock loading are analyzed. Some conclusions are summarized as follows.
(i) Titanium impurity clusters change the formation process and distribution of dislocations. Owing to the higher strength of Ti, the shock wave is obviously hindered from propagating, a high strain zone is formed in front of the Ti cluster. Dislocations are generated from the interface of Ti cluster and move along the{110}slip surface, and the dislocations on multiple slip surfaces together form a grid-like structure. Since the strain concentration reduces the number of dislocation sources,the dislocation density is reduced.
(ii)The Ti clusters have a certain promotion effect on the generation of dislocations. The critical shock velocity of induced dislocation from the Ti-cluster model is lower than from the perfect Al model. Under a shock velocity of 750 m/s,the impact strength is not high enough to induce the dislocation for the perfect Al model,however,the dislocation is generated for the Ti-cluster model due to the non-uniform nucleation mechanism caused by the strain concentration.
(iii) The temperature near the interface of Ti-cluster is higher than in the other areas,which means that the Ti-cluster interface will cause melting earlier than the bulk area. Owing to the obstacle of Ti clusters to the shock waves, unlike the random distribution of high temperature area in the perfect Al model,the high temperature area in the Ti-cluster model is distributed mainly near the Ti clusters and the intersection of dislocations are initiated from Ti clusters.
(iv) With the increase of shock velocity (>1250 m/s),the influence of Ti-cluster on shock response gradually weakens since the impact strength has reached the critical value for Al to generate dislocation and the large scale dislocations have been generated in the bulk Al as well.According to the present results,when the shock velocity increase to 1750 m/s,the temperature is close to the melting temperature and the effect of Ti clusters can be ignored.
Acknowledgment
The authors thank other people or groups for their scientific contributions to this work.
- Chinese Physics B的其它文章
- Numerical simulations of partial elements excitation for hemispherical high-intensity focused ultrasound phased transducer*
- Magnetic-resonance image segmentation based on improved variable weight multi-resolution Markov random field in undecimated complex wavelet domain*
- Structure-based simulations complemented by conventional all-atom simulations to provide new insights into the folding dynamics of human telomeric G-quadruplex*
- Dual-wavelength ultraviolet photodetector based on vertical(Al,Ga)N nanowires and graphene*
- Phase-and spin-dependent manipulation of leakage of Majorana mode into double quantum dot*
- Deep-ultraviolet and visible dual-band photodetectors by integrating Chlorin e6 with Ga2O3

