Magnetic-resonance image segmentation based on improved variable weight multi-resolution Markov random field in undecimated complex wavelet domain*
Hong Fan(范虹) Yiman Sun(孫一曼) Xiaojuan Zhang(張效娟)Chengcheng Zhang(張程程) Xiangjun Li(李向軍) and Yi Wang(王乙)
1School of Computer Science,Shaanxi Normal University,Xi’an 710062,China
2School of Computer Science,Qinghai Normal University,Xining 810003,China
3School of Information Engineering,Xi’an University,Xi’an 710065,China
4Department of Biomedical Engineering,Cornell University,Ithaca,NY 14853,USA
Keywords: undecimated dual-tree complex wavelet, MR image segmentation, multi-resolution Markov random field model
1. Introduction
Magnetic resonance imaging(MRI)[1,2]has the characteristics of arbitrary slice imaging and high soft tissue resolving ability, and can simultaneously perform multi-faceted, multiparameter, multi-sequence imaging, which has become one of the preferred methods for diagnosing diseases. Magneticresonance(MR)image segmentation plays an increasingly important role in the diagnosis and quantitative analysis of medical diseases.However,due to the large amount of information,complicated noise,blurred boundaries,and intensity inhomogeneity of the MR image,the image segmentation still has difficulties and attracts attention of many scholars.
Now, the common algorithms used in MR image segmentation can be roughly categorized as region growing,[3]fuzzy clustering,[4]neural network[5]and Markov random field(MRF),[6,7]etc.Among them,MRF is employed to represent the relationship between images,and uses Bayesian rules to perform image segmentation through mathematical models,which was proposed by Geman and Geman in 1984.[7]Due to the fact that MRF can simulate the intensity non-uniformity appearing in medical image and can be used to describe the spatial information effectively, it has been widely used in the field of medical image segmentation. This kind of algorithms performs MR image segmentation by solving the maximuma posterioriprobability(MAP)of the pixel state distribution.Because the iterated conditional model (ICM) is simple and easy to implement, it is a common method for solving MAP.In recent years, domestic and foreign scholars have proposed some improvement methods based on the Markov random field. For example, researchers[8]proposed the idea of not using iterative methods to maximize posterior probability,and solved the prior distribution of class members in traditional MRF models, which improves the high computational complexity of Markov random field. In Ref.[9],the spatial dependence of segmented labels is introduced in the Markov random field model,and a strategy for automatically segmenting breast MR images is proposed. In Ref. [10], the authors deduced a segmentation technique based on a specific Markov random field class called Pickard random field,which is applied to the segmentation of breast lumps.Compared to other methods,the initialization of this method is straightforward,and the amount of calculation relative to the standard MRF method is greatly reduced.
Although there are many improved algorithms and applications for the Markov random field model, their modeling methods are all spatially non-causal. The present model considers pixels in a first-order or second-order or higherorder neighborhood. The markers of adjacent pixels affect each other and lack the necessary causal relationship. In order to improve the segmentation accuracy of MR images by the MRF model, Leeet al.[11]in 1996 provided an efficient technology for microcalcification detection, which combines multi-resolution wavelet information with image context information extracted by gauss markov random field (GMRF),and then Bayesian learning was achieved by expectationmaximization (EM) algorithm. This method was applied to edge detection of breast images and obtained better results.In recent years, the multi-resolution Markov random field(MRMRF)[12]segmentation method has increasingly applied in medical image processing fields. As in Ref. [13], an image segmentation algorithm based on the MRMRF model was proposed. The multi-scale characteristics of discrete wavelet transform were used to improve the computational efficiency,and the high-frequency edge information after wavelet transform was introduced into the MRF model to improve the segmentation accuracy. In Ref. [14], a medical image segmentation in wavelet domain based on the edge multi-scale domain hierarchical Markov random field model was proposed.The edge was regarded as an observable data sequence,which could preserve edge information and improve efficiency. Although the discrete wavelet transform can represent the multiscale characteristics of the image,and the MRMRF model can be used to simulate the spatial interaction between adjacent pixels to overcome the spatial inhomogeneity in the MR image. There are still problems that depend on the model parameters and the poor direction selectivity.
Aiming at the characteristics and segmentation requirements of MR images,we introduce the multi-scale characteristics of undecimated dual-tree complex wavelet transform[15]on image into the MRMRF model, which solves the problem of poor selectivity of the multi-resolution Markov random field model. The initial clustering center of the K-means clustering algorithm in the MRMRF model is improved by the transformed low-frequency sequence histogram, and then other cluster centers are selected according to the maximum distance rule to obtain the initial segmentation result. Finally,the variable weight is introduced in the MAP criterion to solve the problem that the segmentation result depends on the model parameters,and then the segmentation precision of the MR image is improved.
The rest of this paper is organized as follows. A brief review to the theory of the undecimated dual-tree complex wavelet transform (UDTCWT), and the MRMRF model is given in Section 2. A detailed description of the variableweight multi-resolution Markov random field (VWMRMRF)in this paper is stated in Section 3. Experimental results and analysis are given in Section 4. Clinical MR image segmentation experiments are presented in Section 5. Finally,the main conclusions are drawn in Section 6.
2. Related work
2.1. The undecimated dual-tree complex wavelet transform(UDTCWT)
The dual-tree complex wavelet transform (DTCWT)[16]is oriented and nearly shift invariant, and it can preserve image details better than discrete wavelet transform (DWT).[17]Especially the complex wavelet coefficients have phase information that plays an important role in clinical diagnostic applications,so DTCWT is more suitable for medical image processing. However, the downsampling operation destroys the translation invariance of DTCWT, which means that a small shift in the signal will result in a significant change in the energy distribution of the wavelet coefficients. Therefore, Hillet al.[15]proposed the concept of UDTCWT, which extends the traditional DTCWT using filter upsampling and removing downsampling. Since each sub-band after the transformation has the same resolution as the image itself,the UDTCWT not only has shift invariance, but also provides a one-to-one relationship between the co-located coefficients in all sub-bands and image pixels,which solves the shortage that the traditional discrete wavelet can not represent the detail features of the image well and the direction selectivity is less.[18]The specific decomposition image is shown in Fig.1.
In Fig.1,the first stage filter is a bi-orthogonal filter bank,where the filter (h00,h01) is identical to the filter (g00,g01)but offset by one sample,and none of these filters are upsampled. Subsequent filters are based on the Q-shift filter defined in Ref. [16]. After performing a downsampling operation on each level of decomposition,the upsampling is performed by inserting zeros in the filter coefficients from the second stage.The recursive expression[15]of the filter can be written as

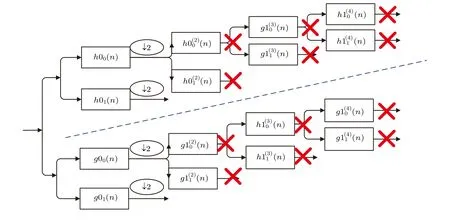
Fig.1. Undecimated dual-tree complex wavelet filter bank.
2.2. The multi-resolution Markov random field(MRMRF)model
Assume that the digital imageyis defined on a gridSof sizeN×N,there areNpbands.
The image is decomposed byJ-layer wavelet. Then, the decomposed image is recorded asWS, and the gridScan be decomposed into
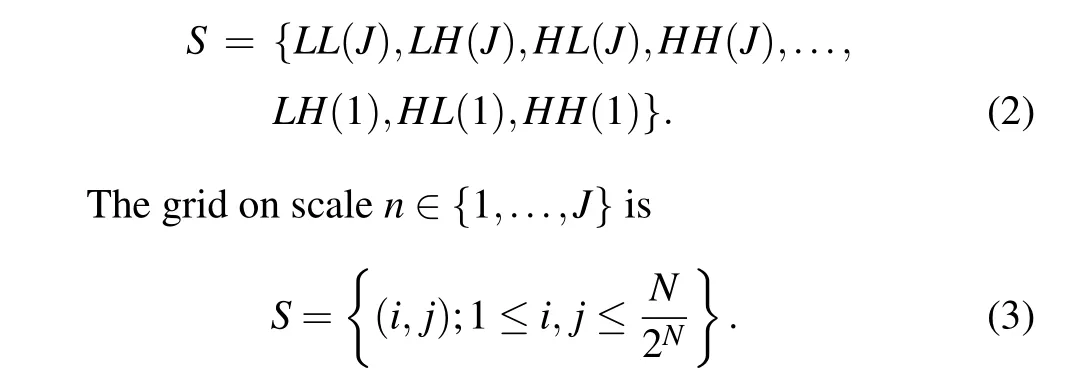
Then, the corresponding mark fieldXnand the feature fieldYncan be defined on the set{S1,...,Sn,...,SJ}. After selecting the appropriate image features as the observed data for each scale, the MRMRF model can be defined onS. The multi-scale feature fields can be written as
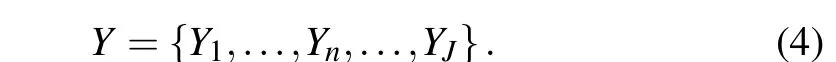
Accordingly, the multi-scale marker field on the set of grid locations for each resolution is expressed as

Assuming that the marker fields are independent of each other,an isotropic two-point MLL(multi-level logic)model is used to calculate the local constraint relationship between the markers. The joint probability distribution of the marker fields can be described by

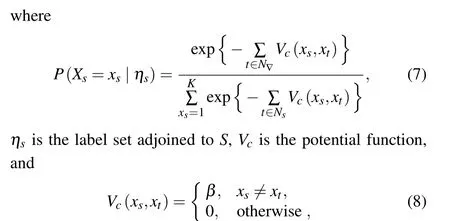
wheresandtare adjacent sites forming a mating site, andβis a positive number.
Assuming that the features on each scale satisfy the conditional independence, and the Gaussian model (GMRF) is used to represent the observation data of each category, the joint probability distribution of all scale feature fields can be expressed as

In order to obtain the optimal segmentation result, after modeling the marker field and the feature field, the estimated values of the segmented image are obtained according to Eqs.(6)and(9),wherein their joint distribution can be expressed as
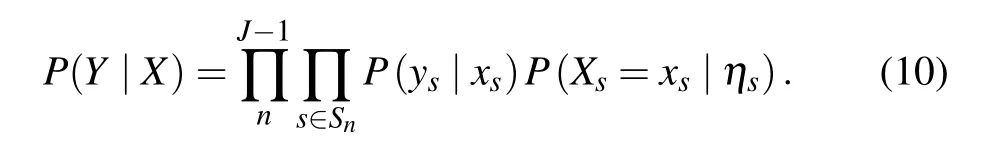
In the image segmentation process, the maximization ofP(Y|X)P(X) is equivalent to the minimization of image energy. Therefore, the multi-scale segmentation of the wavelet domain can use the MAP criterion to derive an appropriate estimate ofX.[12]
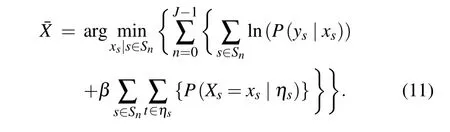
3. Improved image segmentation of variable weight MRMRF
3.1. Image preprocessing
The traditional MRMRF model uses the K-means clustering algorithm to initially segment the image. However,the clustering algorithm is only suitable for the partitions with uniform distribution and obvious features.[19]In order to make the MRMRF model more suitable for MR image segmentation,this paper improves the selection rules of the cluster centers of the original K-means clustering algorithm. The flow chart of improved algorithm is shown in Fig.2.
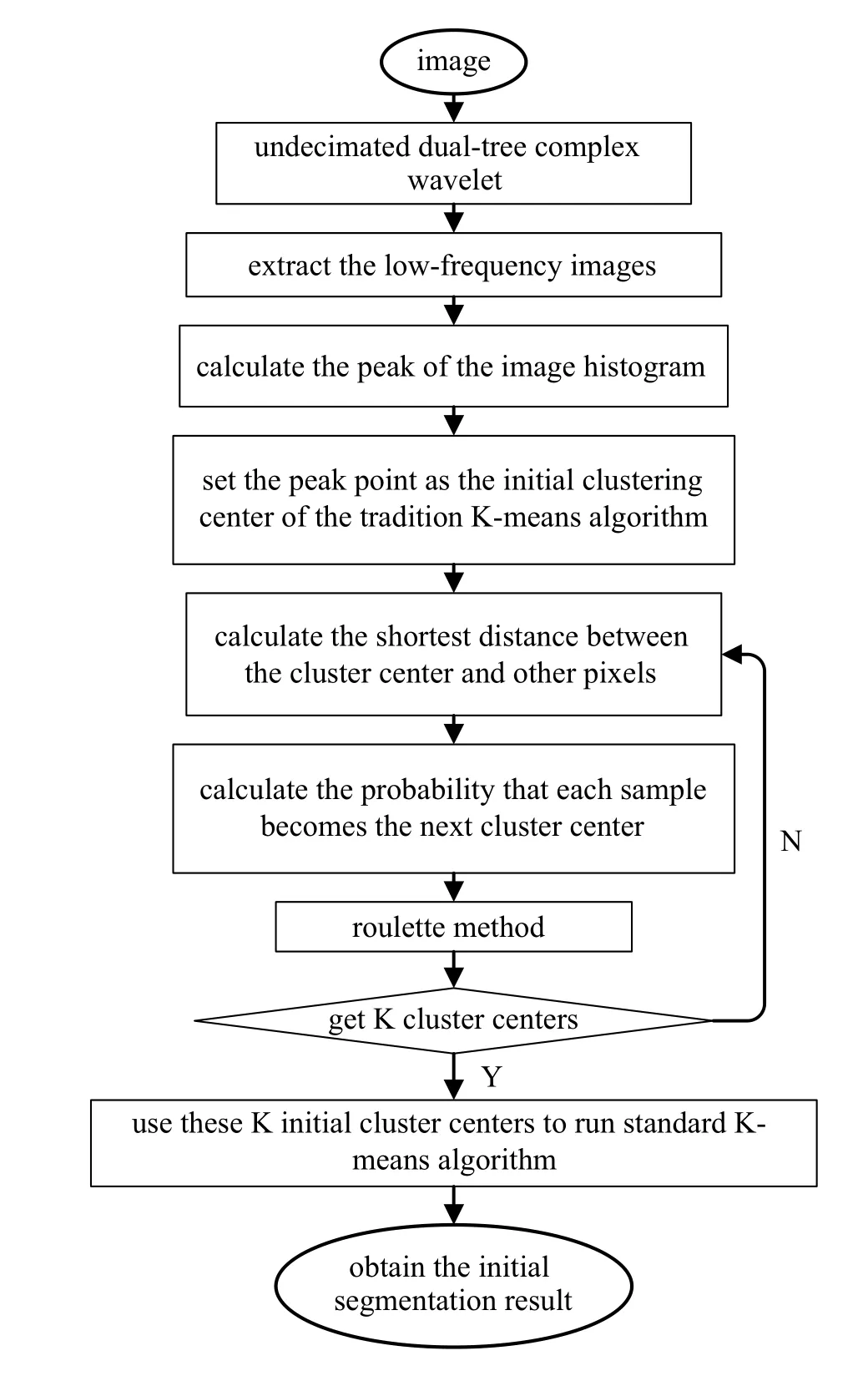
Fig.2. The flow chart of improved K-means algorithm.
Firstly, the image is transformed by the UDTCWT, and the peak of the low-frequency image histogram is used as the initial clustering center of the traditional K-means algorithm to solve the problem that the original K-means clustering algorithm is sensitive to the initial cluster center. Then calculate the distance between the cluster center and other pixels,and put these distances into the set and cluster centers were obtained by roulette method. Finally, use these initial cluster centers to run standard K-means algorithm.
3.2. The variable-weight MRMRF model by undecimated complex wavelet
Wavelet transform is a good time-frequency analysis tool.Discrete wavelet transform can be used to generate multi-scale representation of images,though it has the defects of directivity lack and translation sensitivity.
In this paper,the UDTCWT is used to replace the discrete wavelet transform to enhance the usability of the MRMRF model. On the premise of decomposition of Eq. (2), the image is subjected to UDTCWT decomposition, then two low frequency sub-bandsL(j+1,l),l= 1,2 and six highfrequency sub-bandsD(j+1,k),k= 1,2,3,...,6 of direction(±15°,±45°±75°)can be obtained for each layer. After theJ-layer wavelet decomposition,the gridSdefining the digital image can be decomposed into
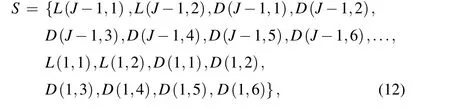
which corresponds to 7J+1 sub-bands ofNpbands inWs.The grid on the scalen ∈{0,1,...,J-1}is
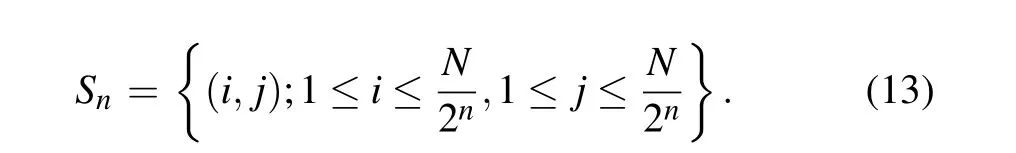
Then the corresponding mark field and feature field can be defined on the mesh set{S0,S1,...,Sn,...,SJ-1}.
In each scale segmentation process, to make the feature field model fit the wavelet coefficient vector field of the scale as much as possible and to obtain the global optimal parameter estimation, a suitable weight must be chosen to combine marker field modeling with feature field modeling (This weight is expressed as the value of the exponent term for each probability in the probability product). It can be seen from Eq. (11) that on each scale, the feature field energy and the marked field energy are linked by a constant weight of 1. If this weight makes the feature field energy play a leading role in the segmentation process,the scale segmentation result will contain more detailed information. If the marker field energy dominates, the regionality of the segmentation result of the scale will be more obvious. In the extreme case,unpredictable segmentation results will occur. Therefore, a variable weightα(t,n)is introduced in Eq.(11)(tis the number of iterations,nis the scale),Eq.(11)is improved to
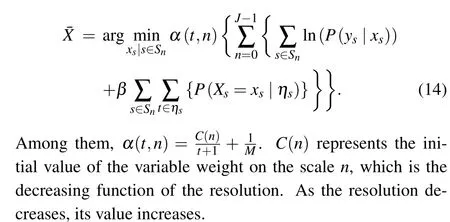
At large scale (low resolution), the feature field energy is given in a larger weight, which makes it dominate in the initial stage of segmentation and is beneficial to obtain the global model parameters of the feature field. As the iteration progresses, the weight gradually decreases, the effect of the marker field energy gradually increases,the parameters are gradually optimized, and the segmentation result is gradually improved. After the iteration is carried out to a certain extent,the weight becomes constant,and the two energies reach equilibrium,which acts together on the segmentation process until the end of the iteration. The process of parameter variation is equivalent to producing a better initial segmentation at various scales for the traditional MRMRF model.
3.3. Algorithm implementation
In order to solve the MR image segmentation problem under the MRMRF model,we carry out the multi-scale transform of image by undecimated dual-tree complex wavelet transform, and improve the initial clustering center of the Kmeans algorithm using the transformed low-frequency scale histogram. Then, we select cluster centers according to the maximum distance rule to obtain the coarse scale segmentation result, which will be segmented by the VWMRMRF model. The algorithm flow chart is shown in Fig.3.

Fig.3. The flow chart of the VWMRMRF model in the UDTCWT domain.
The specific process can be expressed as follows.
Step 1Give the number of classificationsM, the potential functionβof the MLL model. The image is decomposed byJ-1 layer undecimated dual-tree complex wavelet decomposition and the feature fields of each scale are formed in the manner shown in Subsection 2.2. Set the iteration stop condition of the expectation-maximization (EM) algorithm. Set the value of the scaling functionC(n) in descending order of scale.
Step 2Cluster the feature field vectors on the scaleJ-1 to obtain the initial segmentation result of this scale according to the improved K-means clustering algorithm.
Step 3Estimate the meanμmand covariance matrix ∑nmof the feature field of the scaleJ-1 by the EM algorithm,then GMRF feature field model is established. Since the training data cannot be used to estimate parameters in an unsupervised environment, the EM algorithm is used to perform parameter estimation.[20]The maximizing pseudo-likelihood(MPL) method with high computational efficiency is used to obtain the GMRF model parameters. The parameter iteration is shown as follows:
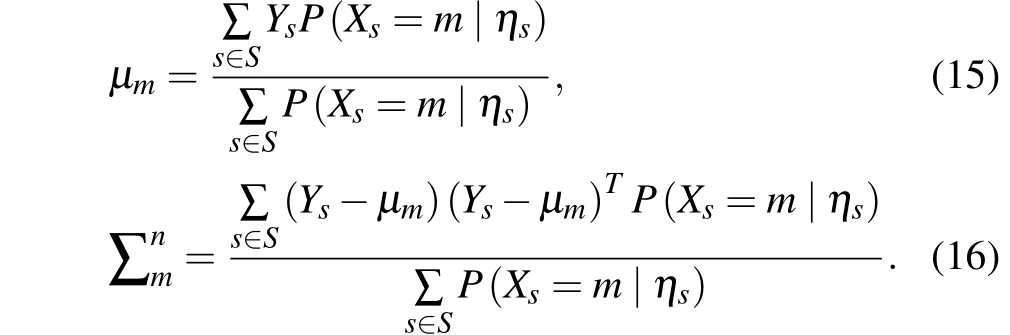
Step 4Use the estimated parameters to calculate the feature field energy weightα(t,n)of the current iteration number on the scalenby the ICM algorithm with faster calculation speed, and the one-step optimized segmentation result on the scale is obtained according to Eq.(14).
Step 5Repeat steps 3 and 4 until a certain criteria is met,then the iteration stops, and the final segmentation result on scalenis obtained.
Step 6The segmentation result of the scalenis directly mapped to the nearest neighboring fine scalen-1 as the initial segmentation of this scale. Repeat step 5 until the segmentation result on the finest scale is obtained.
4. Algorithm performance analysis
The performance of the MR image segmentation based on the VWMRMRF in the UDTCWT is verified in this section.We analyze the aspects of anti-noise performance, segmentation accuracy and time complexity. For qualitative comparison of the performance of the VWMRMRF and comparison algorithm, this paper uses the maximum number of iterations(MaxIter=200)as the iterative termination condition of all algorithms. All experiments are implemented respectively in Matlab 2016a programming environment on a 2.50GHz CPU,4G RAM,Intel(R)Core(TM)i5-2400 personal computer and Windows7 Ultimate 64-bit.
4.1. Anti-noise performance analysis
During magnetic resonance imaging, the real and imaginary parts of the signal are simultaneously interfered by Gaussian noise of the same variance with zero correlation,the noise of the MR image often appears as a Rician distribution,[21]whose probability density function is as follows.

When the SNR approaches to 0(m/σ →0),the Rician distribution is Rayleigh distribution, when the SNR approaches to∞(m/σ →∞),the Rician distribution is Gaussian distribution.
Adding Rician noise with SNR=20 to the synthetic image shown in Fig. 4(b), the ICM algorithm and the MRMRF algorithm are compared with the proposed VWMRMRF algorithm, and set the potential functionβ=0.5. The segmentation results are shown in Figs.4(c)-4(e).
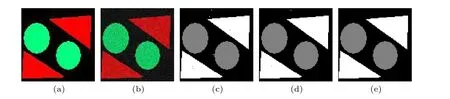
Fig.4. Clustering results of noisy images: (a)original image;(b)noise image;(c)ICM;(d)MRMRF;(e)VWMRMRF.
In order to test the anti-noise performance of the VWMRMRF on MR images, we conduct the experiments on T1-weighted sequences of the simulated brain database[22]with 1 mm slice thickness, 0% intensity inhomogeneity level, and 0%, 1%, 5%, 9% noise levels, shown as column 1, rows 1-4 of Fig.5. The brain is mainly composed of three components:gray matter(GM),white matter(WM),and cerebrospinal fluid(CF). The white matter is the paler tissue of the brain and spinal cord,consisting mainly of nerve fibers with their myelin sheaths. The gray matter is the darker tissue of the brain and spinal cord,consisting mainly of nerve cell bodies and branching dendrites. Cerebrospinal fluid is the clear watery fluid which fills the space between the arachnoid membrane and the pia mater.
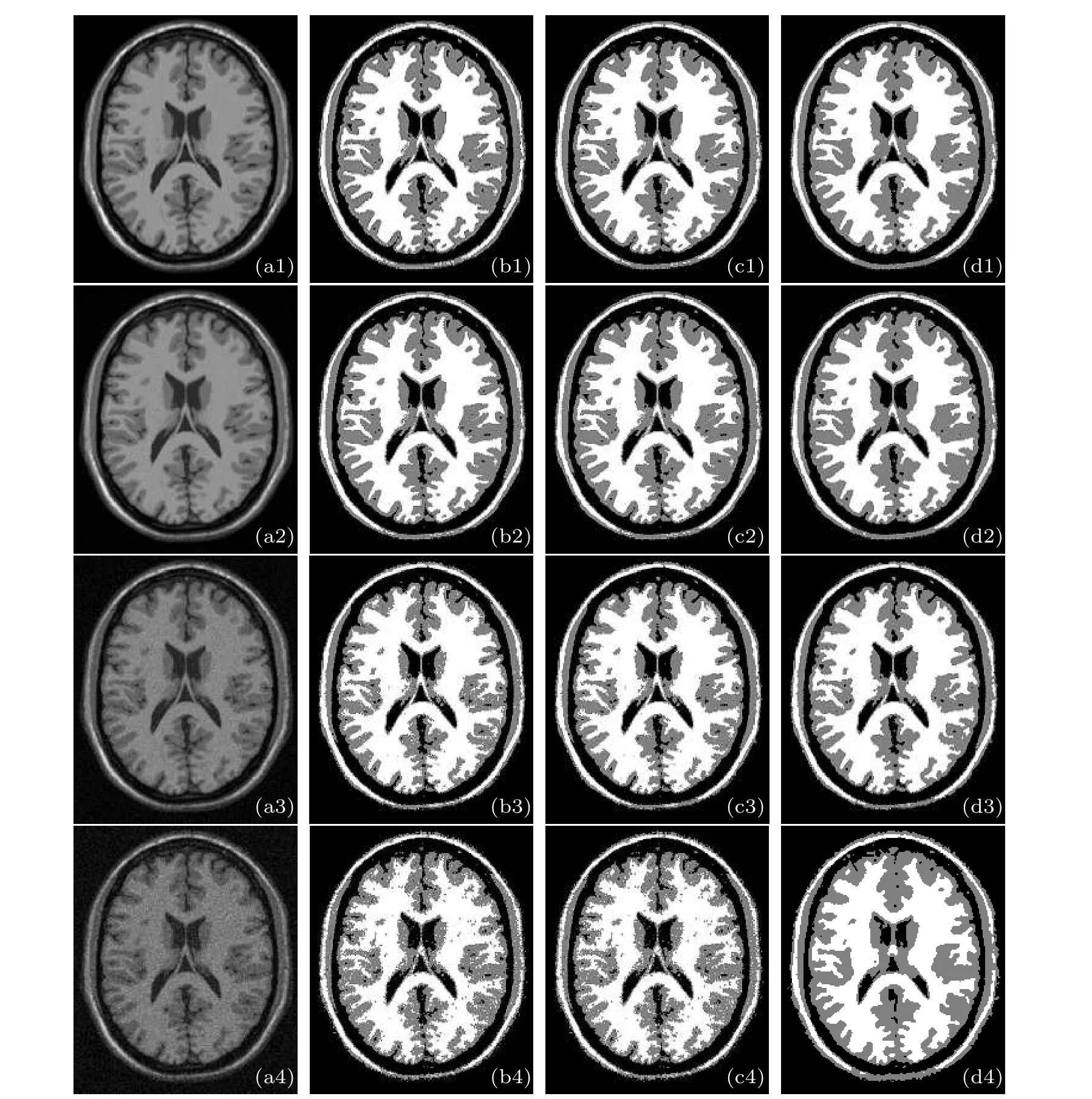
Fig. 5. Segmentation results of the T1-weighted stimulated brain images with different noises. The column 1 is the original images added different noise levels: (a1) 0%; (a2) 1%; (a3) 5%; (a4) 9%. The segmentation results of (b1)-(b4) ICM, (c1)-(c4) MRMRF, (d1)-(d4)VWMRMRF.
From Fig.5, we can see that the three algorithms are all anti-noise, which can basically distinguish the white matter(WM) and gray matter (GM) regions from noise. However,the segmentation results of the ICM algorithm are still not satisfactory because they show various misclassifications as the noise increases. In contrast, the MRMRF and the VWMRMRF algorithm provide better segmentation results as the degree of misclassification is much less than the ICM algorithm.Especially,the segmentation results of the VWMRMRF are more accurate and clear, which indicates that the VWMRMRF algorithm has better anti-noise performance. The values of the peak signal-to-noise ratio (PSNR) in Table 1 also quantitatively illustrate that the VWMRMRF has the stronger anti-noise performance,PSNR can be defined as[23]
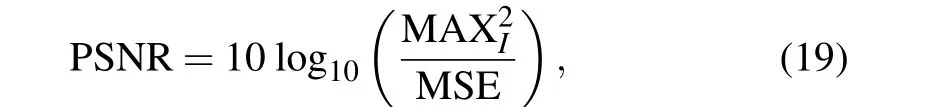
where MAX is the maximum value of pixel points,MSE is the mean square error of the original image and the segmentation image,andIis the pixel value of the original image.
Table 1. The PSNR values for T1-weighted stimulated brain images with different noises.
In addition, the Dice coefficient (DC) is also a similarity measure function in the image segmentation process. The values of the Dice coefficient in Table 2 are used to evaluate the quality of the segmentation result. The Dice coefficient is calculated by[24]
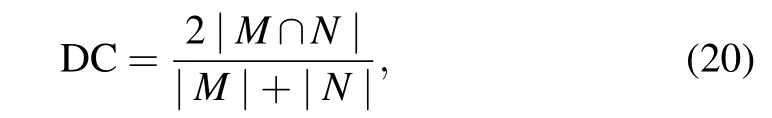
whereMis a nonzero gold standard andNis a nonzero segmentation result. The larger the DC value,the better the segmentation result.
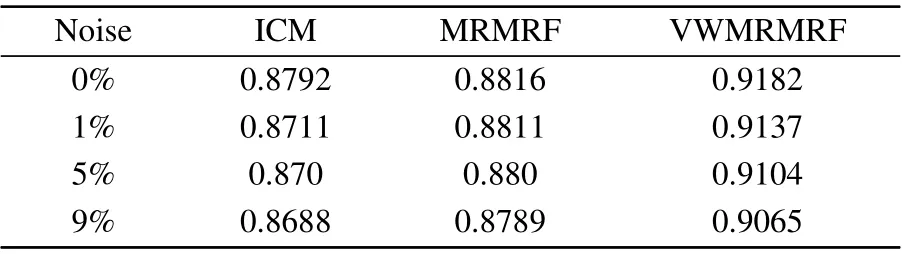
Table 2.The Dice coefficients for T1-weighted stimulated brain images with different noises.
From Tables 1 and 2, we can see that the VWMRMRF not only has good anti-noise performance,but also has the best segmentation effect.
4.2. Segmentation precision analysis
In order to verify the segmentation accuracy of MR images in this method, the Brain Web database and the T1 weighted image of the UNC Infant 0-1-2 Atlases database were used. The layer thickness of image is 1 mm. The basic information of the dataset is shown in Table 3.

Table 3. Information of each dataset.
The VWMRMRF is used to segment brain structures,including gray matter, white matter, and cerebrospinal fluid, as shown in Fig.6(taking the image of a 1-year-old child in UNC as an example). For highlighting the organizational structure,we select the 84th slice of the sequence in which the image is located.
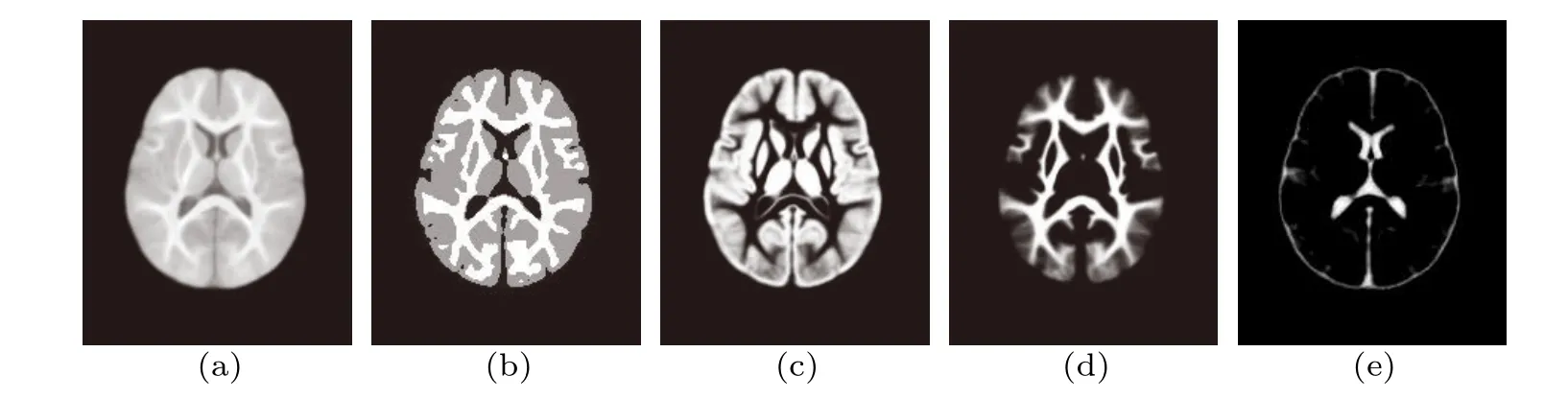
Fig.6. Brain structures and segmentation gold standards in UNC(take the image of a 1-year-old child as an example): (a)original image;(b)split gold standard which is the ground truth;(c)gray matter;(d)white matter;(e)cerebrospinal fluid.
The evaluation of the segmentation results in this study is mainly carried out in three aspects: vision, time and Dice coefficient. Among them,the visual evaluation mainly judges whether the image is wrongly divided,whether the area is consistent,and whether the edge is intact.

Table 4.The results of the VWMRMRF on two data sets under different potential functions,the evaluation index Dice.
The values of different potential functionsβare used to segment the random 20 groups of images in the two data sets and to calculate the average dice coefficient value to verify the segmentation performance of the VWMRMRF algorithm in this paper. The experimental results are shown in Table 4.In this section, two image segmentation results are taken for analysis,as shown in Figs.7 and 8. Figure 7 presents the segmentation results under different potential functions where the row 1 is the brain image of the Brain Web and row 2 is the UNC brain image. Figure 8 shows the segmentation results of the brain images of the Brain Web and UNC by the VWMRMRF and the comparison algorithm when the potential functionβ=1.
From the results of different potential function segmentation,when the value of the small potential function is selected(β=0.2), it is difficult to fully consider the interaction between the neighborhoods in the image segmentation process because the effect of the markers field is too small,resulting in poor regionality of the segmentation results. If a larger potential function is used(β=5),the interaction between the markers is magnified,resulting in a very good regional consistency of the segmentation results.Because of this,the unpredictability of the segmentation results is enhanced. However, not only other segmentation results corresponding to some potential functions maintain regional consistency,but also regional boundaries can be detected more accurately. In this paper,the effect of the marker field and the feature field are weighed according to the scale,so that the segmentation process not only fully considers the relationship between the neighboring pixels,but also does not cause the marker field to act too much and the boundary deformation occurs. Therefore,variable weights can balance both boundary information and good regional consistency.
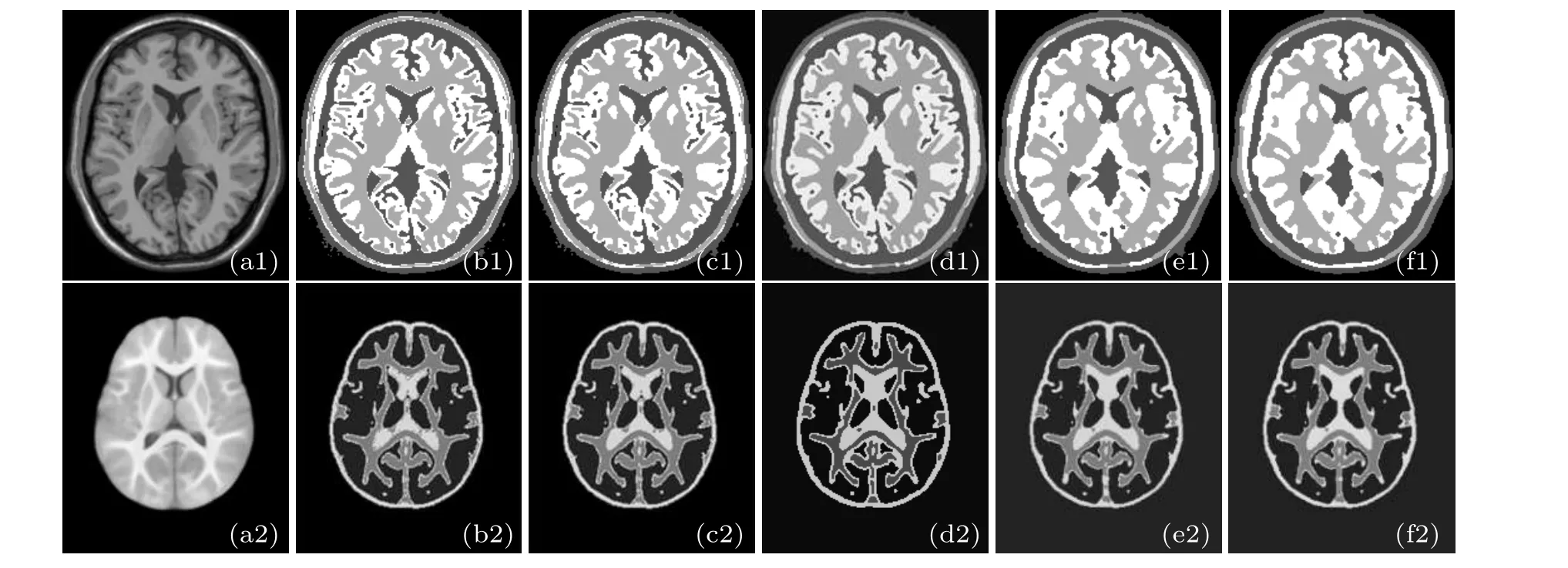
Fig.7. Image segmentation results of two data sets under different potential functions. The row 1 is the brain images of Brain Web and the row 2 is the UNC brain images. (a1)The original image of Brain Web; (b1)β =0.2; (c1)β =0.5; (d1)β =1; (e1)β =2; (f1)β =5; (a2)the original image of UNC;(b2)β =0.2;(c2)β =0.5;(d2)β =1;(e2)β =2;(f2)β =5.
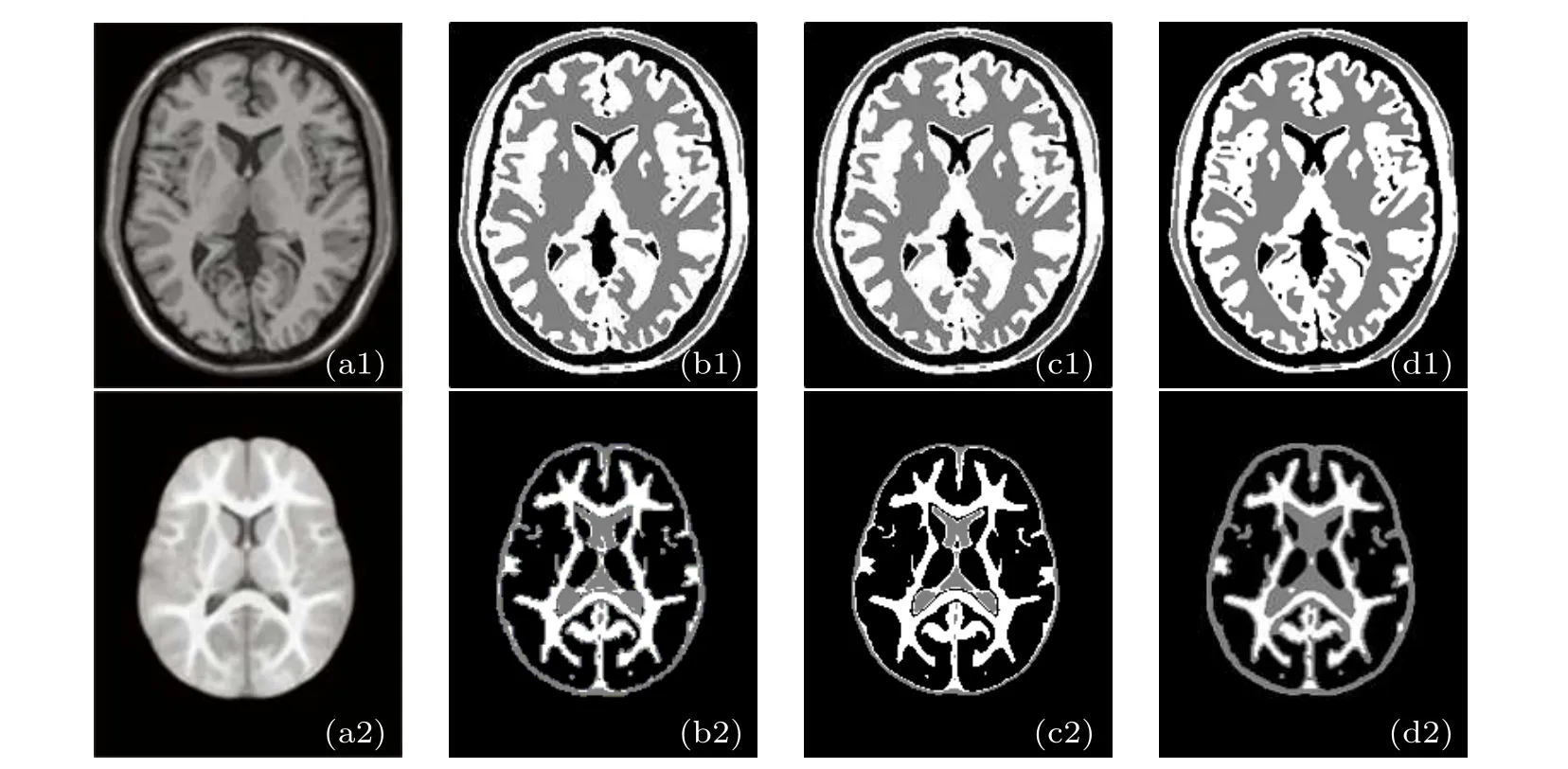
Fig.8.Segmentation results of image under the same potential function β =1.(a1)The original image of Brain Web;(b1)ICM;(c1)MRMRF;(d1)VWMRMRF;(a2)the original image of UNC;(b2)ICM;(c2)MRMRF;(d2)VWMRMRF.
Under the same potential function,the contrast algorithm ICM segmentation effect is quite unsatisfactory. Not only the edge segmentation is blurred,but also the brain tissue has a serious over-segmentation phenomenon. Although the segmentation result of the MRMRF algorithm is better to divide the internal tissue,the division of the edge details is still unclear.The segmentation results of the VWMRMRF are more satisfactory than the comparison algorithm. Not only the outline of the brain image is clearly segmented, but also the edges remain intact, the details are divided accurately, and there is no over-segmentation or under-segmentation. Combining the dice coefficient values given in Tables 4 and 5,it can be seen that the VWMRMRF algorithm achieves satisfactory segmentation results compared with the comparison algorithm.

Table 5. The results of the VWMRMRF and the comparison algorithm on the two data sets,the evaluation index Dice.
In order to further describe the segmentation effect of the algorithm on the brain MR image, the brain MR images in three orthogonal views(transversal,sagittal,and coronal)from the simulated brain database are shown in Fig.9. This data set is selected from the Brain Web anti-shock brain MR image database of the Brain Imaging Center of the Montreal Neurological Institute of McGill University. It provides ground truth for all brain MR images, so it can truly demonstrate the segmentation effect and robustness of the algorithm in this paper.
We select multiple sclerosis(MS)Lesion Brain Database in Brain Web. The parameters are:T1 sequence diagram,slice thickness 1 mm,noise level 0%,intensity non-uniformity 0%.The number of classifications is 4, and the potential function is set toβ=1. Figures 9(c)-9(e) show the segmentation results. Combining the Dice coefficients given in Table 6, we can see that the VWMRMRF has a better segmentation effect in any orthogonal views of the brain. The segmentation results of simulated brain MR images verify the performance of the VWMRMRF algorithm once again.
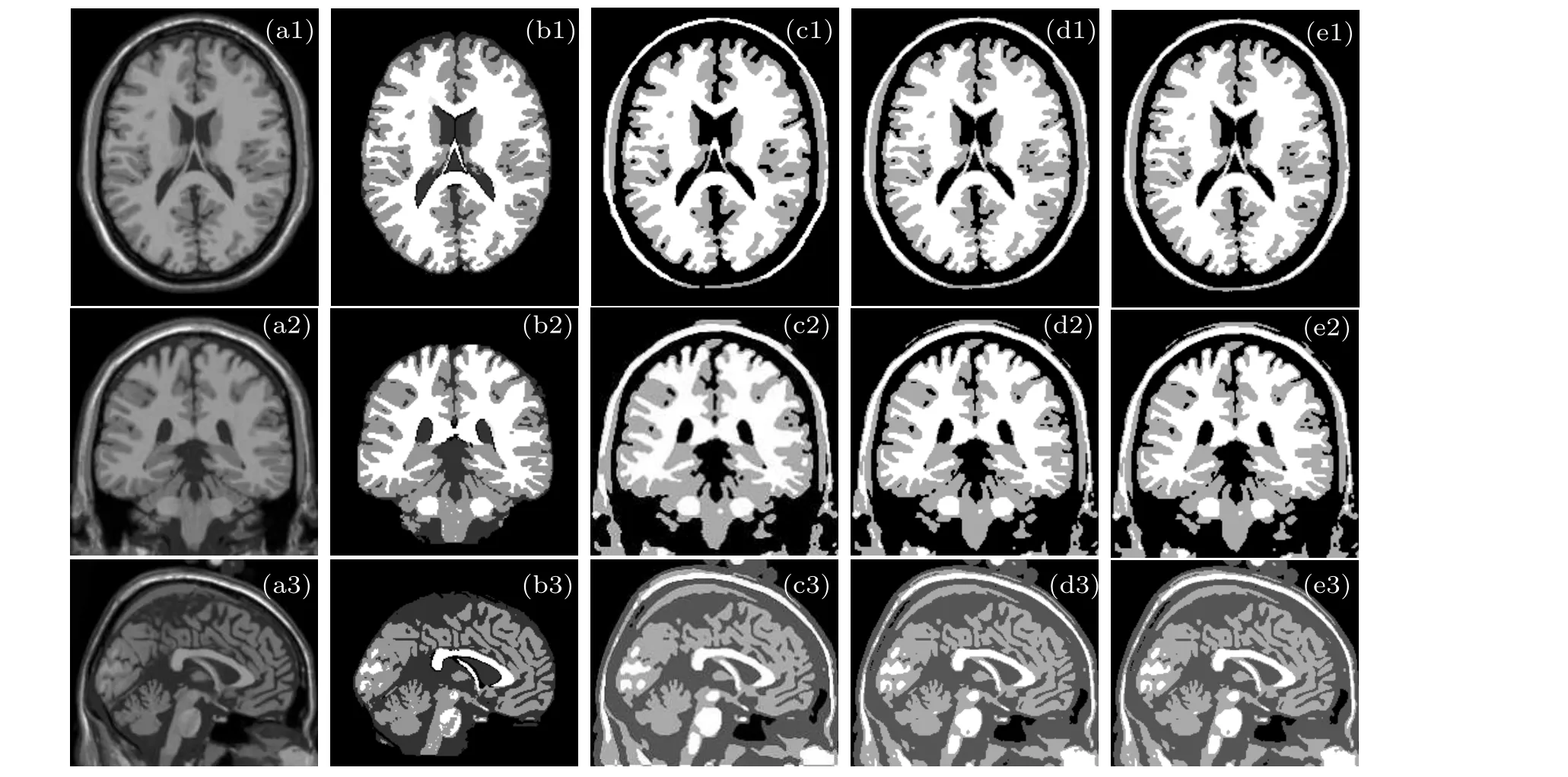
Fig.9. Segmentation results of simulated brain image. (a1)Transverse plane; (a2)coronal plane; (a3)sagittal plane; (b1)-(b3)ground truth;(c1)-(c3)ICM;(d1)-(d3)MRMRF;(e1)-(e3)VWMRMRF.
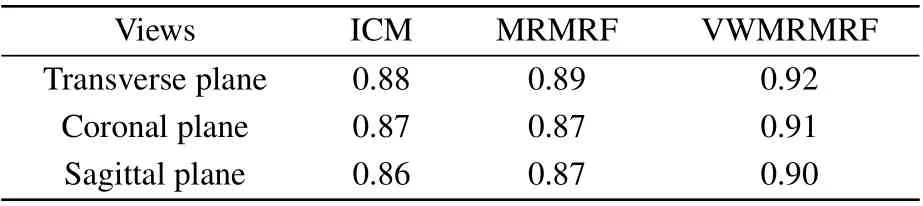
Table 6.The Dice coefficients for T1-weighted stimulated brain images in three orthogonal views.
4.3. Time complexity analysis
In the VWMRMRF algorithm,suppose that the input image size isN×N, and the time complexity of the algorithm mainly comes from the three stages: feature extraction,initial segmentation and MRF modeling.Feature extraction is implemented by undecimated dual-tree complex wavelet transform with a time complexity ofO(NJ),whereJis the number of decomposition layers,andJ ≤N. Therefore,the feature extraction time complexity isO(N). The initial segmentation uses the K-means clustering algorithm, and its time complexity isO(N2Km), whereKrepresents the number of divided categories,andmrepresents the dimension of the feature vector,K,m ≤N2. Therefore,the time complexity of the initial segmentation isO(N2),and the time complexity of MRF modeling isO(TN2K), whereTrepresents the number of iterations. In a word,the total time complexity of the segmentation algorithm is similar toO(TN2K).
Table 7 shows the running times of the ICM, MRMRF and VWMRMRF algorithms in Figs. 4 and 8. It can also be seen from the segmentation time in Table 7 that the multi-scale transformation of the image by wavelet transform is adopted in the algorithm,which results in the time consumed in the whole algorithm to be slightly longer than that of the ICM algorithm.However,it is better than the MRMRF algorithm. We change the discrete wavelet decomposition in the traditional MRMRF to the undecimated dual-tree complex wavelet decomposition,which reduces the amount of data and can improve the computational efficiency. Therefore, if the real-time requirement is not very high in the field of image segmentation,it is meaningful to exchange the relatively long time for the anti-noise performance and the segmentation precision.

Table 7. The average running time of each algorithm segmentation in Figs.4 and 8.
5. Clinical MR image segmentation analysis
During the imaging process,the clinical MR image is affected by external factors such as temperature and magnetic field,and the image presents a series of shortcomings such as uneven gray scale and weakened boundary, which bring certain difficulties to image segmentation,although Section 4 has verified the performance of the VWMRMRF through images in databases such as Brain Web.
5.1. Segmentation of breast MR images
MRI has unique imaging advantages in breast examination: Firstly, it has very high sensitivity. Secondly, MRI can perform tomographic and arbitrary three-dimensional imaging. Thirdly,it can show the parts that cannot be displayed by mammography. Finally, dynamically enhanced scan images and time-signal intensity curves can help us understand the blood perfusion,diffusion,and vascular penetration of the lesion,which is helpful for clinical differentiation of benign and malignant. Therefore,in this section,the algorithm is applied again to the segmentation of the clinical breast MR image in DICOM format as shown in Fig.10,to verify the performance of the algorithm.
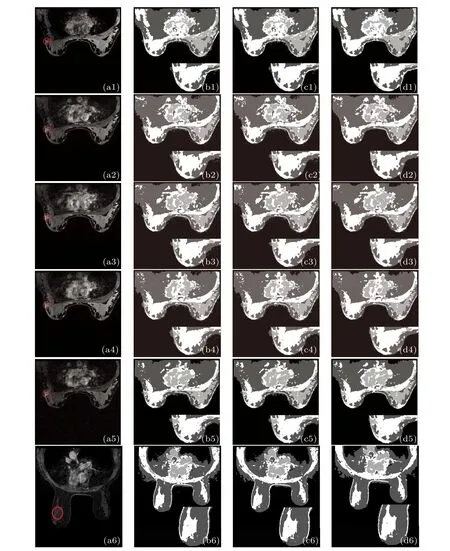
Fig.10.Clinical breast MR image segmentation results.(a1)The original image of the uninjected contrast agent;(a2)-(a5)the images acquired in time series after injection of contrast agent; (a6)the enhanced tumor image of another patient; the segmentation results of(b1)-(b6)ICM;(c1)-(c6)MRMRF;(d1)-(d6)VWMRMRF.
The mammography MR images in Fig. 10(a) were obtained from the German Siemens 1.5 T standard double breast coil magnetic resonance scanner. The experimental images are the three-dimensional T1 weighted gradient echo sequence diagram before and after enhancement. The first row is the image of the uninjected contrast agent, rows 2, 3, 4 and 5 are images acquired in time series after injection of contrast agent, row 6 is the enhanced tumor image of another patient.The patient is in prone position during scanning and imaging, and the bilateral mammary glands naturally hang in the cavity of the breast coil. The parameters are: TR=5.6 ms,TE=2.76 ms,layer spacing 0.3 mm,layer thickness 1.2 mm,FOV=34×34 cm,image size 512×512. The scanning was repeated 5 times, each dynamic scan time is 60 s. The second dynamic scan was started 20 s after the first dynamic scan is completed. At the same time, a high-pressure syringe was used to inject 0.2 mmol·kg-1of Gd-DTPA(glucuronide injection)through the back of the hand at the rate of 2 ml·s-1. The rapid injection is completed within 10 s.Then at the same rate,physiological saline of 20 ml was injected to flush to push the contrast agent into the human circulation. The red circle in the image is the tumor area,and the number of classifications is 4.
Figures 10(b)-10(d) show the segmentation results of ICM, MRMRF and VWMRMRF, respectively. In order to show the results more clearly, the segmentation of the breast associated with one side of the tumor is magnified in the lower right corner of Figs. 10(b)-10(d). Among them, algorithm ICM potential functionβis set to 4 (because the segmentation effect is best at this time). The potential functionβof the MRMRF and the VWMRMRF algorithm is also set to 4.It can be seen from the segmentation results in Fig.10 that the three algorithms fail to segment the tumor region for non-enhanced images, whereas the VWMRMRF achieves better edge segmentation than the other algorithms. For the enhanced image,the tumor is not completely segmented in the ICM algorithm segmentation result,and the large area around the tumor is divided incorrectly. Although the MRMRF segmentation effect is improved compared with the ICM algorithm, the tumor is more completely segmented. However, the segmentation effect is also not ideal,and over-segmentation occurs at the edge of the image. In contrast,not only the VWMRMRF algorithm in this paper segments the tumor accurately, but also the surrounding area of the tumor is basically divided correctly and the contour relatively is clear. The segmentation results verify that VWMRMRF is more effective for segmenting breast MR images and has certain application value in the diagnosis of breast diseases.
5.2. Segmentation of brain MR images
In actual medical image segmentation, multi-modal images are more commonly used for diagnosis. In order to test the applicability of our algorithm on multi-modal images,we select the BraTS2018[25-27]which runs in conjunction with the medical image computing and computer-assisted intervention (MICCAI) 2018 conference as a challenge to facilitate the development of brain tumor segmentation methods. It includes 4 pulse sequence data: native (T1), post-contrast T1-weighted (T1Gd), T2-weighted (T2), T2 fluid attenuated inversion recovery (FLAIR), which are acquired with different clinical protocols and various scanners from multiple(n=19)institutions.Figure 11(a)shows the original images of the four modalities. There is a lesion area in the original slice, whose ground truth is shown in Fig.11(b). Figures 11(c)-11(e)show the segmentation results of ICM,MRMRF and VWMRMRF,respectively.
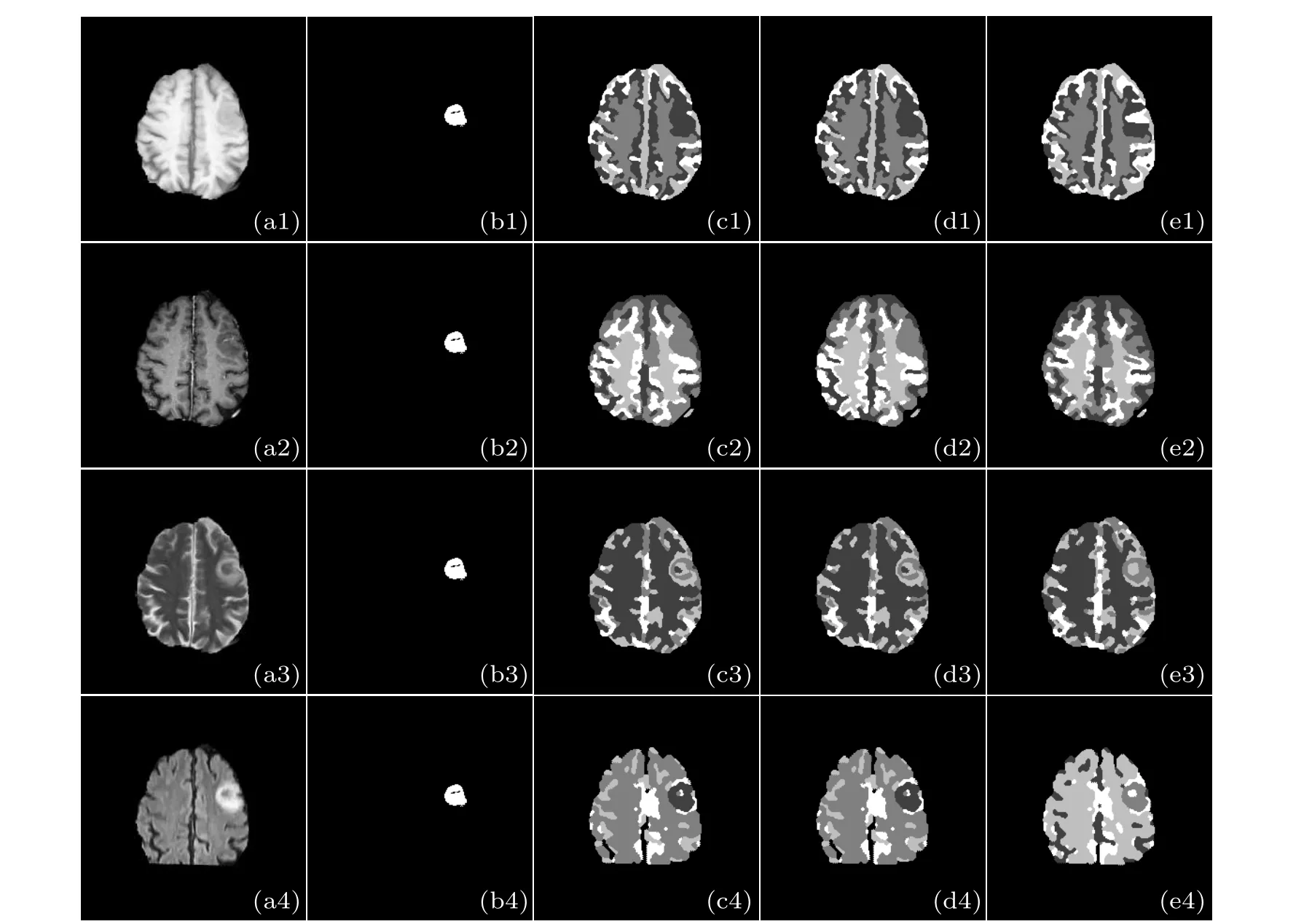
Fig.11. The segmentation results of multi-modal brain MR images. The first column is the original image of the different modalities where(a1)T1;(a2)T1Gd;(a3)T2;(a4)FLAIR;(b1)-(b4)ground truth;(c1)-(c4)ICM;(d1)-(d4)MRMRF;(e1)-(e4)VWMRMRF.
For the T1 and T1Gd, comparison algorithms ICM and MRMRF basically did not segment the tumor area, while VWMRMRF segmented part of the edge information of the tumor. For the T2 and FLAIR, the three algorithms all segment the tumor area and details,but the over-segmentation of the comparison algorithms is more obvious. Relatively speaking, the segmentation effect of VWMRMRF is better and the segmentation areas are more complete. Because it is difficult to guarantee the generalization of the segmentation method due to the difference of MRI contrast images, one algorithm does not fit all modalities well, and the segmentation results are not very satisfactory. The VWMRMRF algorithm has a better segmentation effect on any modalities of the brain MR images than comparison algorithms, while it is still not very ideal. It will be our focus in the future.
6. Conclusion
In summary, we have proposed an improved MR image segmentation algorithm based on MRMRF in undecimated dual-tree complex wavelet domain. The algorithm draws on the multi-directionality and translation invariance characteristics of the undecimated dual-tree complex wavelet. According to the characteristics of the low-frequency image histogram,the algorithm overcomes the problem that the existing algorithm is easy to fall into local optimum due to the poor directionality and dependence on the initial clustering center. The variable weight function is introduced in the segmentation process, which effectively solves the problem that the algorithm uses the fixed potential function which causes the algorithm to be ignored in the relationship between the neighboring pixels, so that the final segmentation result is not good. The experimental results show that the VWMRMRF algorithm has better anti-noise performance,higher precision and robustness for MR image segmentation. It can effectively segment MR images.
Acknowledgment
The authors thank the teachers,friends and all the members of the machine learning and data mining laboratory who provided them with support and help. Also,the authors would like to sincerely thank all the referees for their general and detailed comments and suggestions, which is helpful for improvement of this paper.
- Chinese Physics B的其它文章
- Numerical simulations of partial elements excitation for hemispherical high-intensity focused ultrasound phased transducer*
- Structure-based simulations complemented by conventional all-atom simulations to provide new insights into the folding dynamics of human telomeric G-quadruplex*
- Dual-wavelength ultraviolet photodetector based on vertical(Al,Ga)N nanowires and graphene*
- Phase-and spin-dependent manipulation of leakage of Majorana mode into double quantum dot*
- Deep-ultraviolet and visible dual-band photodetectors by integrating Chlorin e6 with Ga2O3
- Extended-source broken gate tunnel FET for improving direct current and analog/radio-frequency performance*

