Juan Zhao(趙娟) Da-Guang Yue(岳大光) Lu-Lu Zhang(張路路) Shang Gao(高尚)Zhong-Bo Liu(劉中波) and Qing-Tian Meng(孟慶田)

1School of Science,Shandong Jiaotong University,Jinan 250357,China

2School of Physics and Electronics,Shandong Normal University,Jinan 250358,China

Keywords: state-to-state,time-dependent quantum wave-packet method,differential cross sections

1. Introduction

The H+H2reaction and its isotopic variants have been the focus of numerous experimental[1-7]and theoretical[8-17]studies over many years. In the field of molecular reaction dynamics, the construction of potential energy surface (PES) is very important. For H+H2system, there are a lot of works about PES.As early as in 1978,Truhlaret al.have developed LSTH surface[18]with 267ab initiopoints and a maximum absolute deviation of 0.55 kcal/mol.In 1987,Varandaset al.performed complete-active-space self-consistent field(CASSCF)and multireference configuration interaction calculation and gave an adiabatic double many-body expansion(DMBE)PES for H3.[19]In 1994,Sunet al.carried out quantum mechanical calculations of the rotational excitation of H2by H atoms using the DMBE[19]PES and found that the low temperature thermal rate coefficients were significantly higher than those based on the LSTH[18]surface.In order to investigate the origin of these discrepancies between these two H3PESs, Boothroydet al.developed an improved surface (BKMP),[20]which matched the 772ab initioenergies with a maximum absolute deviation of 1.21 kcal/mol. BKMP surface incorporated new data extending toRH-H2=4a0,but it too was least well constrained in the critical range ofRH-H2. In 1996,Boothroydet al.fitted a refined H3PES,denoted as BKMP2[21]surface,this PES was based on 8701ab initioenergies with an overall root-meansquare(rms)error of 0.17 kcal/mol and a maximum absolute deviation of 3.90 kcal/mol. In 1999, Wuet al.[22]calculated a new surface based on spline fits of an exact quantum Monte Carlo method.

Based on these five surfaces,numerous theoretical studies of the H3system have been done, among which the BKMP2 surface is most widely used[23-27]for the reason that in accurate quantum calculation, it can produce a very good agreement result with the experiment.[2,3,28-31]In 1997,Hochman-Kowal and Persky[32]studied the influence of rotation on reactivity for the H+DH(v= 0,j= 0-6) on the LSTH and DMBE PESs using the quasi-classical trajectory method. In 2002, Chaoet al.[3,28]presented the results of a joint experimental and theoretical investigation of the reaction dynamics of the H+DH′→D+HH′chemical reaction,and found that the experimental and theoretical state-to-state dynamics are in quantitative agreement.

The above researches mainly focus on H+DH′→D+HH′channel, but the collisions between H and DH may generate products through two reaction channels: the abstraction channel that produces the production of H2(H+DH′→HH′+D)and the exchange channel that leads to the production of HD (H+DH′→HD′+H), the study of exchange channel H+DH′→HD′+H is few. In addition, Hanet al.[33]developed a parallel code for state-to-state quantum dynamics with propagation of time-dependent wave-packet[34,35](TDWP)in reactant coordinates based on graphical processing units(GPUs),and this code has been used to calculate the differential cross sections(DCSs)of H+H2reaction based on the BKMP2 surface and state-resolved reaction probabilities of nonadiabatic triplet-singlet transitions of O(3P,1D)+H2[33]for the total angular momentumJ=0. These results show that the calculation accuracy is high and the calculation speed is fast,which solves the time-consuming and memory limitation problems that have troubled researchers for a long time due to the large amount of state-to-state quantum calculation.So far,this code has been successfully used to study the quantum state-to-state dynamics of O(3P)+HD,[36]S+H2,[37]N+H2,[38]N+HD,[39]F+HO,[40]D+ND[41]reactions.

In this work,we used this efficient GPUs version of timedependent wavepacket code to calculate the product stateresolved integral cross sections (ICSs) and differential cross sections of H+DH′→HH+D′and H+DH′→HD+H′reaction channels. The paper is organized as follows: in Section 2, we will give the theoretical methodology used in this work.Section 3 will present the results and discussion.Finally Section 4 will close with the conclusions.

2. Theoretical method

In this contribution, the efficient GPUs version of TDWP[33]code is used. This code has been successfully applied to many studies on the state-to-state dynamics properties ofA+BCsystem.[36-43]The main idea of this method is as follows. The Hamiltonian of the title reaction is defined in the body-fixed(BF)reactant Jacobi coordinates. For a givenJ(Jis total rotational angular momentum),the Hamiltonian of theA+BCreaction can be expressed as

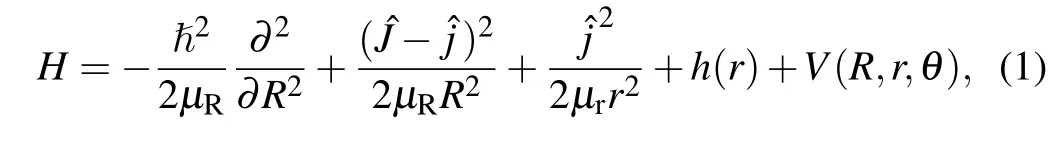
The corresponding reduced massμRis expressed asμR=mA·(mB+mC)/(mA+mB+mC), andμrcan be written asμr=mB·mC/(mB+mC). ?Jis the total angular momentum operator, and ?jis the rotational angular momentum operator ofBC.V(R,r,θ)=Vpes-Vr(r),whereVpesis the potential energy of the triatomic system,andVr(r)is the diatomic potential energy ofBC.h(r)is the diatomic reference Hamiltonian defined as

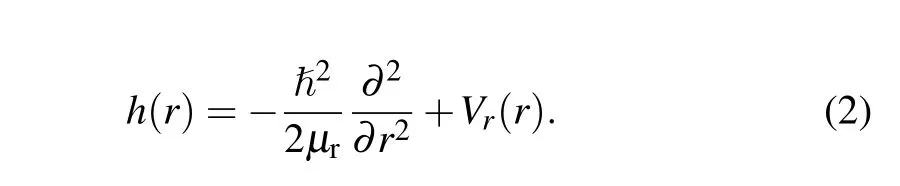
The initial Gaussian wave packet for the reactant in the spacefixed(SF)reactant Jacobi coordinate is expanded as:

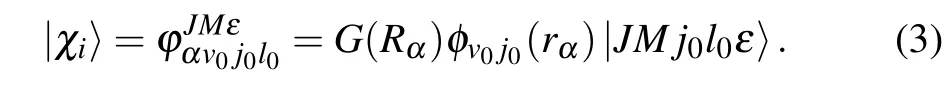
For the initial state (v0j0l0),|JM j0l0ε〉represents the SF rotational basis and describes angular motion,withMbeing the projection of the total angular momentumJ.φv0j0(rα)is the rovibrational eigen-function of the diatomic moleculeBC.The initial wave packet is transformed into the BF frame and propagated on GPUs with the second-order split method.[44]The absorbing potentials with the form of damping functions are employed to prevent the reflections of the wave packet from the boundaries. To extract the state-to-state information of the product channels, the handicap of the reactant Jacobi coordinate based method is the coordinate transformation from reactant to product channel, and the radial component of product wave-packet is a delta function multiplied the outgoing asymptotic radial functions

whereR∞is the location of the dividing surface in the product asymptote where the transformation proceeds. The basic idea of the transformation is to carry out the projection from the wave packet in the reactant Jacobi coordinate(R∞,rα,θα,Kα)to the product Jacobi coordinate (R∞,ri,θj,Kβ) through the equation,withKαandKβbeing the projection of the total angular momentumJin the BF reactant and product coordinates,respectively. So,the scattering matrix element in BF representation is defined as

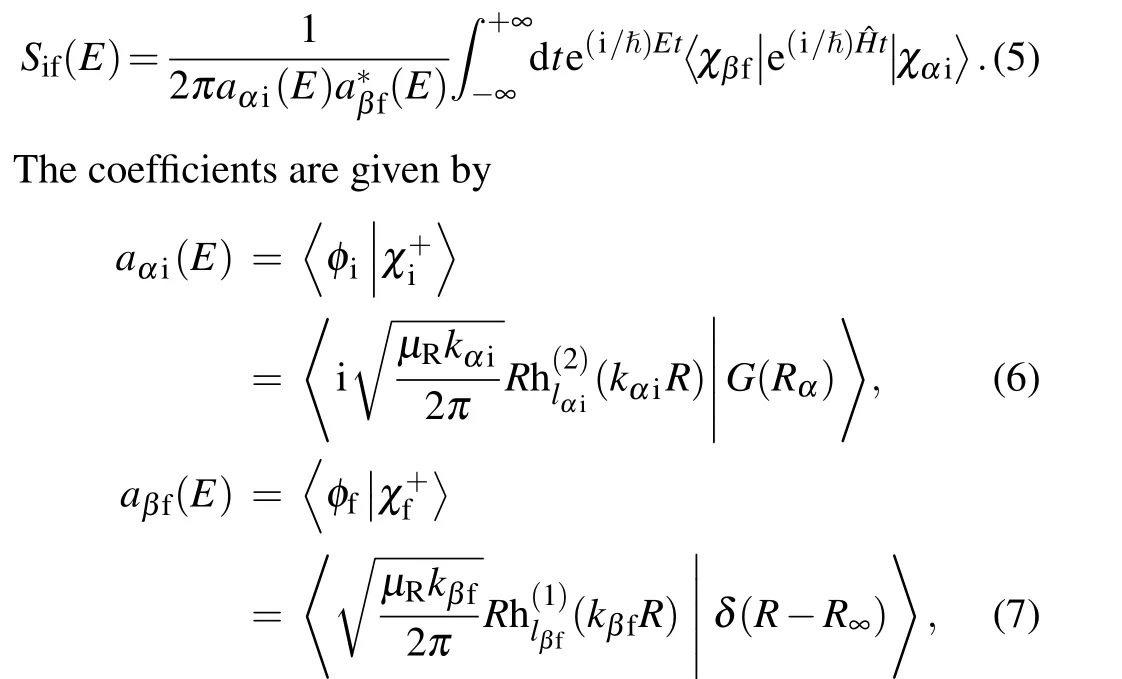
where h(1,2)are the spherical Hankel functions of the first and second kinds.Finally,the scattering matrix is transformed into helicity representation to derive the DCS and ICS by a scattering matrix summing over all relevant total angular momentum quantum numbersJ.

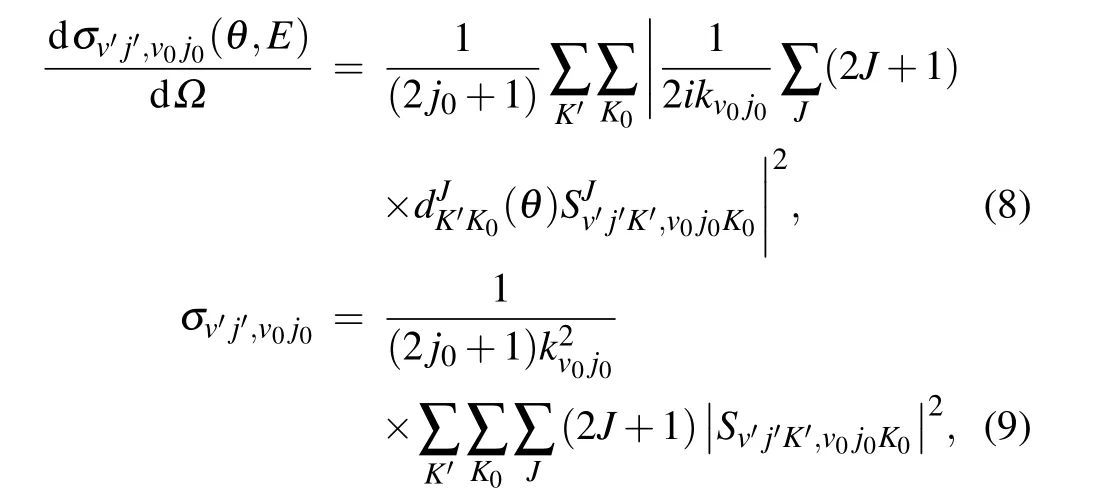
wherekv0j0is the translational wave vector of the initial state(v0,j0).θis the scattering angle anddJK′K0is the Wigner rotational matrix. More theoretical details can be found in Ref.[33].

In present work,we carry out state-to-state calculation for all angular momentumJup to 30 to converge differential cross sections of the title reaction for the collision energy range of 0.15 eV-1.0 eV. To insure convergence of scattering results,extensive tests have been carried out to determine the optimal parameters,which are summarized in Table 1. One of the key convergence parameters in this work is denotedK, which is set (J+1), including all the projection of the total angular momentumJ.

Table 1. Numerical parameters used in the present quantum wave packet calculations.

3. Results and discussion

3.1. Reaction probability and integral cross section

Figure 1 shows the minimum energy path (MEP) of H3 BKMP2 PES.As is shown in Fig.1,there is a barrier with the height of 9.61 kcal/mol(≈0.42 eV).[21]

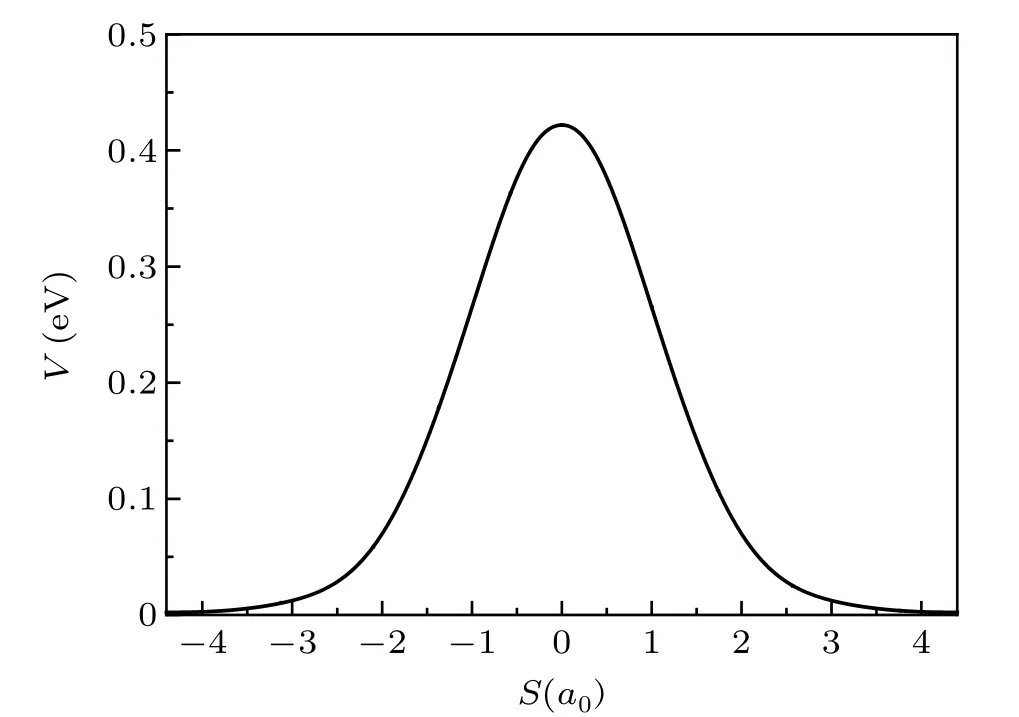
Fig.1. Minimum energy path of the BKMP2 PES.

Firstly, in order to verify the correctness of our calculations, the ICSs summed over final states of H+DH′→HH′+D and HD+H′reaction channels and the rotational state-resolved ICS of H+DH′→HH′+D at the collision energy of 0.5 eV are calculated, and the results are shown in Figs.2(a)and 2(b),respectively. In Fig.2(a),the green dashdot line are TDWP results of H+DH′→HH′+D, the blue dash-dot-dot line are TDWP results of H+DH′→HD+H′channel in this work, and the other results are cited from Refs. [28,32]. As shown in Fig. 2(a), all the ICSs present a similar trend,i.e., each of them increases with increasing relative translational energy and has a threshold at energy of about 0.35 eV. Due to the quantum tunneling effect, the threshold energy is smaller than the height of barrier. There are also differences between the two reaction channels in Fig. 2(a). The reaction section value of the HD+H′channel is larger than that of the HH′+D channel at the collision energy higher than 0.5 eV. There are two possible reasons;one is the zero-point energy(ZPE)effect, the other is the deviation of the center of mass of the reactant molecule DH′.For H+DH′reaction system, the force constant of the reaction system is the same, but the vibrational frequency of HD substitute is lower than HH′,so the harmonic ZPE of the HD molecule is lower than HH′, the H+DH′→HD+H′is easier to occur, and the cross section is larger. Moreover,from a classical point of view, the center of mass of the reactant molecule DH′is closer to the D atom, so when H atoms collides with DH′molecule,the probability of H atoms hitting D will be greatly increased, resulting in the formation of HD products more easily, and the integral cross section of HD+H′is larger than that of the HH′+D product channel. Figure 2(b) shows the rotational state-resolved reaction cross sections of H+DH′→HH′+D reaction channel atEC=0.5 eV, the black squares are quantum-mechanical results with Boltzmann spin statistics reported by Chaoet al.,[28]the red circles are experiment results, the blue stars are the TDWP results in this work. On the whole,these results agree well with each other, but from the details, it can be seen that our results forj′=1,2,4 are closer to the experimental values than the ones obtained by Chaoet al.

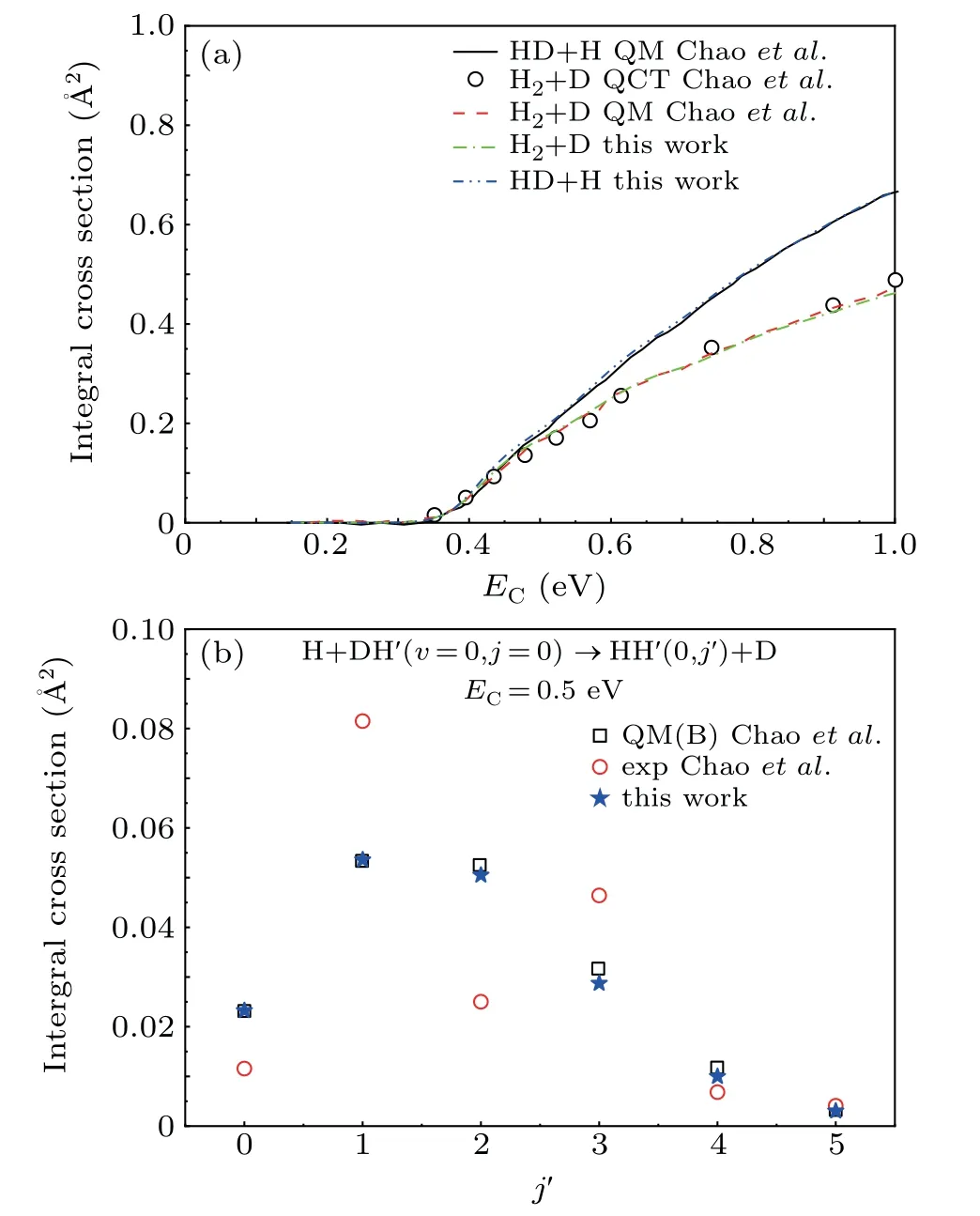
Fig.2. (a)Total ICSs versus collision energy. The early QM results are from Chao and Skodje (Ref. [28]), the QCT results are from Hochman-Kowal and Persky(Ref.[32]). (b)The ICS for H+DH′(v=0,j=0)→HD(v′ =0,j′)+H′ versus j′ at EC =0.5 eV. The red circles are the experimental results(Ref.[28])and black squares represent the results of QM using Boltzmann statistics(Ref.[28]).

To shed light on theJdependence of the total reaction probabilities, we plot the reaction probabilities as a function of total angular momentum at eight collision energies in Fig.3.TheJ-dependent partial wave contribution is weighted over a(2J+1) factor to the ICS. It is well known that theJdependence of the ICS is an analog of the opacity functionp(b),wherebis the collision parameter. Thus, differentJdependence means different impact parameter dependence. All the opacity functions are smoothly varied and exhibit similar arch shapes. The curves follow the trend that increases withJ,reaches the maximum and subsequently drops to zero when reaching the largest accessible value. Meanwhile, the curves extend to largerJvalues with increasing collision energy. It is also seen that for certain collision energy, largeJpartial waves are involved in the H+DH′→HH′+D channel, and in particular we can see from the vertical value that the bigger contributor to the H+DH′→HD+H′channel is the smallerJ. According to the one-to-one correspondence between the impact parameterband the angular momentumJ,it is reasonable to consider that collisions with large impact parameters are in favor of the abstraction reaction,while those with small impact parameters lead to the exchange reaction.[43]Therefore, the direct abstraction mechanism is more dominant in H+DH′→HH′+D channel than H+DH′→HD+H′.

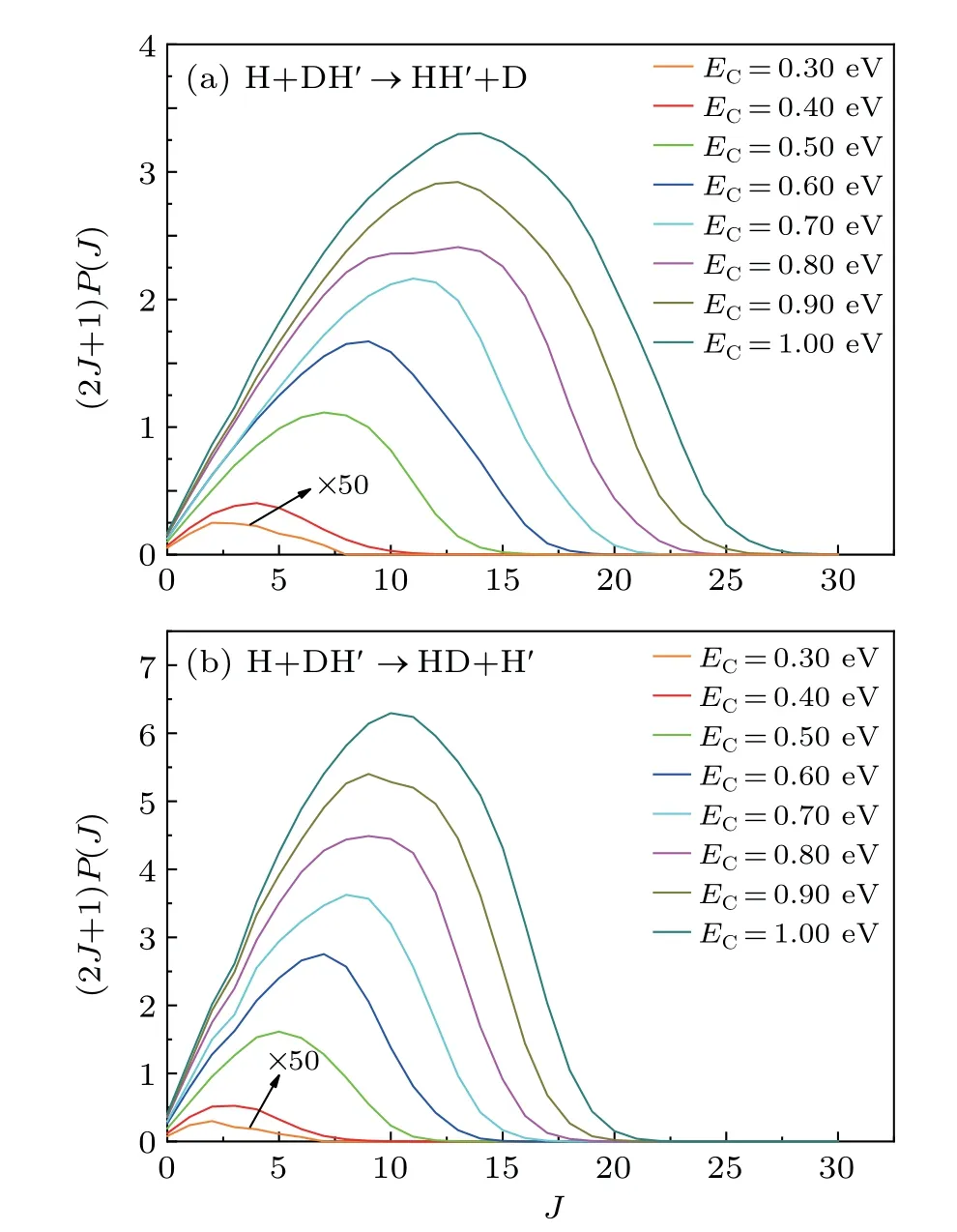
Fig.3. (2J+1)weighted opacity functions for(a)H+DH′→HH′+D and(b)H+DH′→HD+H′ at different collision energies.

3.2. Product distribution

Figure 4 shows the vibrational state-resolved reaction cross sections of the products HH′and HD at the collision energy range of 0.15 eV-1.0 eV. As can be seen from Fig. 4,the products of both channels are mainly concentrated in thev′=0 vibrational energy level. For HD product, because of lower vibrational frequency,the vibrational energy level of the product molecule can be reached is larger (v′=2, and 1 for HD and H2,respectively).

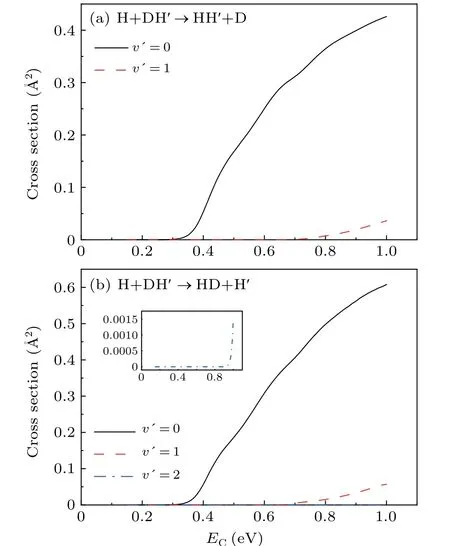
Fig.4. Vibrational state-resolved reaction cross sections for(a)H+DH′ →HH′+D and(b)H+DH′→HD+H′ reactions.

The rotational state-resolved reaction cross sections of two product channels are also been calculated and shown in Fig. 5. There is a similar collision energy threshold (≈0.35 eV) for both reaction channels, and when the collision energy is greater than the threshold, the rotational quantum number inversion occurs in both reaction products. The difference is that the HD product channel can achieve a greater maximum rotational quantum number than the HH′channel.Because the direct mechanism plays a major role in both reaction channels, and each atom in the system has a light mass,so the orbital angular momentum of the reactants can easily be converted into the rotational angular momentum of the of the product molecules. Considering that the mass of atom D is higher than that of atom H,according to the rotational energy formula,

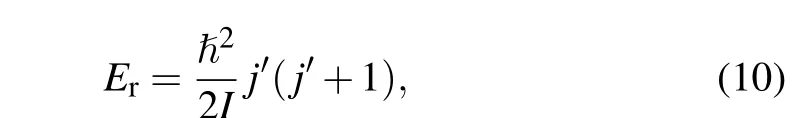
the gap of rotational energy level of the HD molecule is small,and therefore, the maximum rotational energy level that the HD product molecule can achieve is larger.

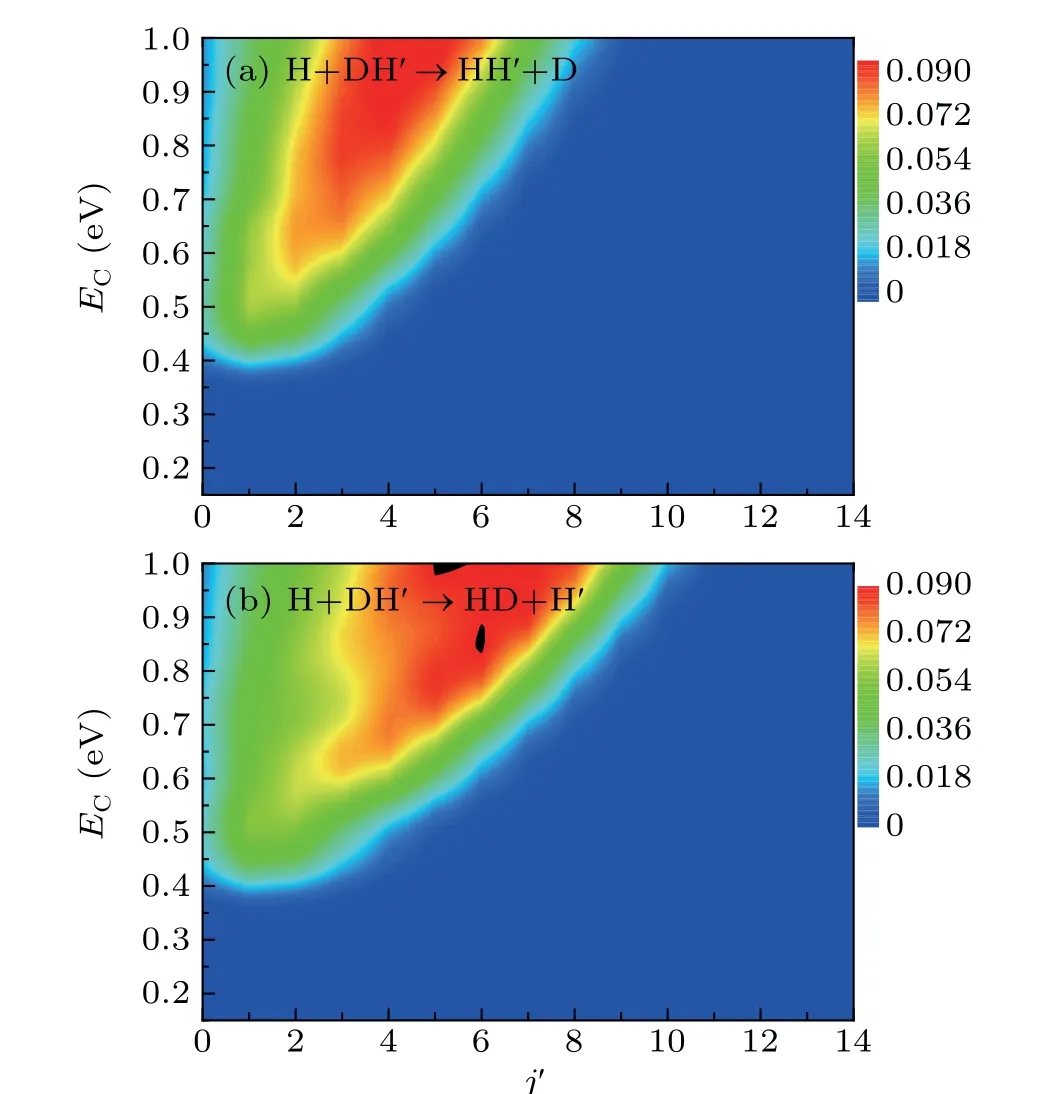
Fig. 5. Rotational state-resolved reaction cross sections for (a) H+DH′ →HH′+D and(b)H+DH′→HD+H′ reactions.

In order to more intuitively display the state distribution of product molecule, we plot the vib-rotational distribution at different collision energies for H+DH′→HH′+D and H+DH′→HD+H′channels in Figs.6 and 7,respectively. It can be seen in these two figures that the vib-rotational distributions are like a half-cooked egg for both channels,the product’s vibrational quantum number is essentially 0, and with the collision energy increasing,this half-cooked egg gets fatter and fatter,i.e.,the collision energy can promotes the rotational rather than vibrational excitation of the product molecules. In addition, it can also be seen from the difference between the Figs.6 and 7 that the maximum rotational quantum number of HD achieved is greater than that of H2. During the reactive encounter,total angular momentum is conserved

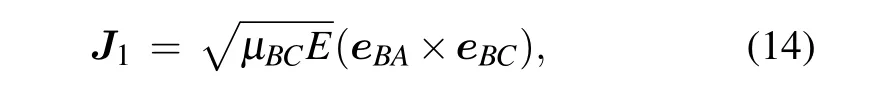
eBAandeBCare unit vectors withBpointing toAandBpointing toC,respectively;μBCis the reduced mass ofBCmolecule andEis the repulsive energy,the larger product atom will take more angular momentum away. Considering these two reaction channels in this work,j=0 and twoJ1s are the same.But for H+DH′→HH′+D,

so the rotational quantum numberj′of HD achieved is greater than that of HH′. In order to compare the energy level intervals quantitatively, we calculated the rotational energy levels of both the HH′(v′=0,j′) and HD(v′=0,j′) molecules by solving the radial Schr¨odinger equation of nuclear motion,and the results are shown in Table 2.From this table,it can be seen that HD has much smaller gaps of the rotational energy level.

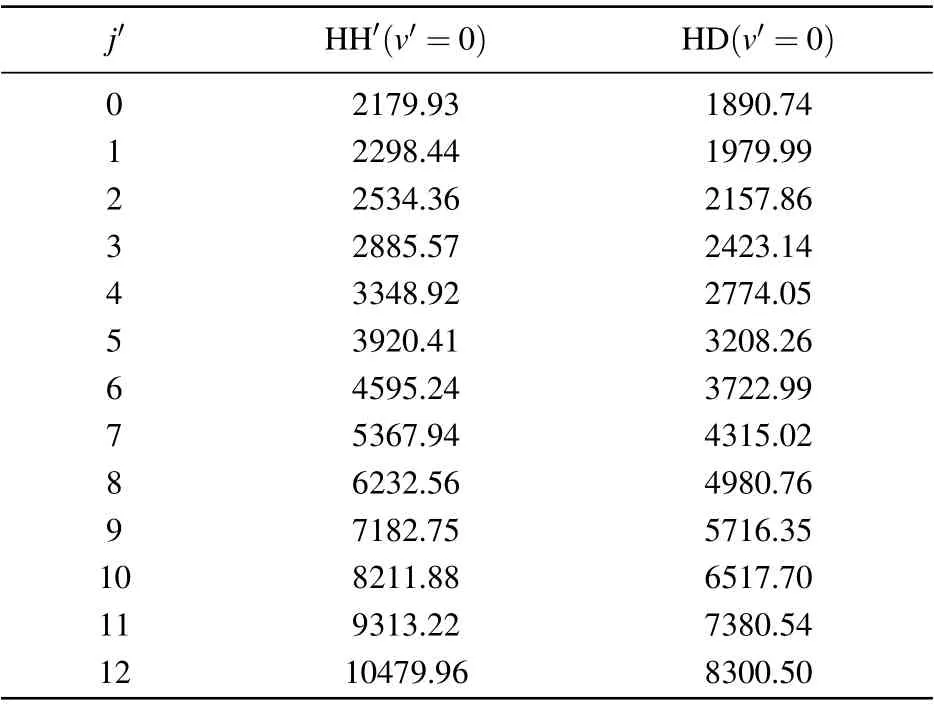
Table 2. The vib-rotational energies(in units of cm-1)of the HH′ and HD product molecules.

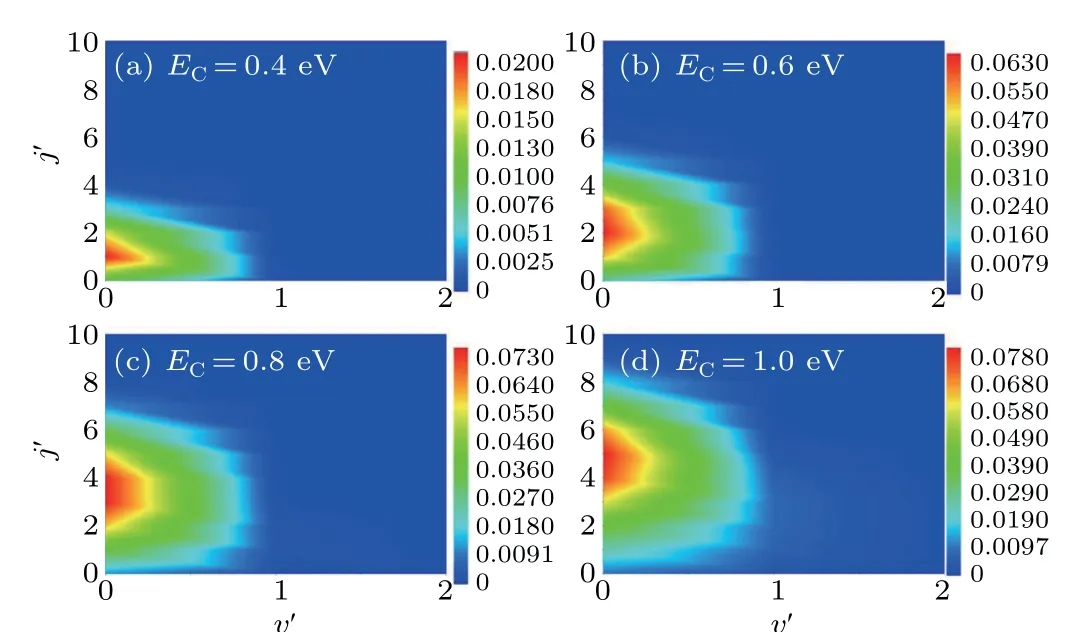
Fig. 6. Product vib-rotational state-resolved distributions for H+DH′ →HH′+D reaction at four collision energies(a)EC=0.4 eV,(b)EC=0.6 eV,(c)EC=0.8 eV,and(d)EC=1.0 eV.

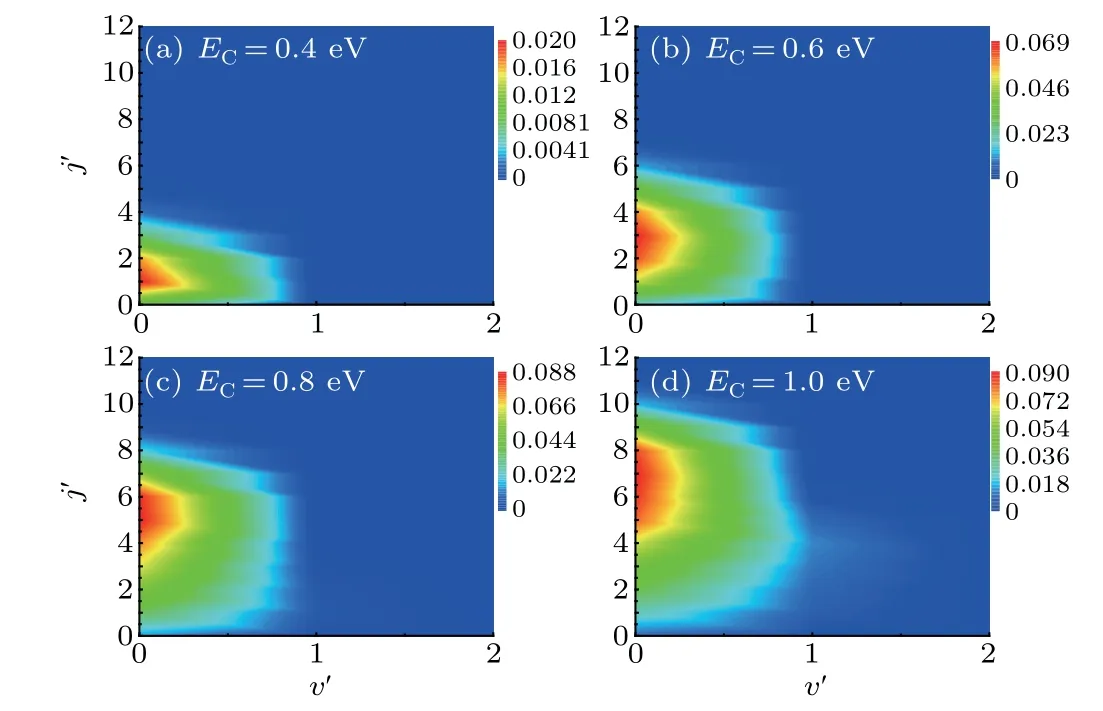
Fig.7. The same as Fig.6 but for H+DH′→HD+H′ reaction.

3.3. Differential cross sections

Figures 8(a) and 8(b) display the total DCSs of H+DH′→HH′+D and H+DH′→HD+H′reaction channels at four collision energies, respectively. As can be seen in Figs. 8(a) and 8(b), the product of both channels are mainly backscattered, and with the collision energy increasing, the backward scattering is enhanced. Of course,there are some differences between these two channels. For H+DH′→HH′+D channel,the range of scattering angle is larger,and forEC=1.0 eV,a more obvious forward scattering phenomenon appears in H+DH′→HH′+D channel. These results are consistent with the usual rebound mechanism in a system with a collinear reaction path. Moreover, the center of mass of the reactant molecule DH′is closer to D, if the H atom approaches the reactant DH′, it has a greater chance to get closer to D atom, and the reaction is controlled by the rebound mechanism, which leads to a larger scattering angle for HD product molecule than HH′. As the collision energy increases, larger number of partial waves are involved in the reaction[42]as shown in Fig.3,which suggests that the contribution from the direct abstraction mechanism becomes larger,the scattering angle becomes smaller and the products start to scatter forward.

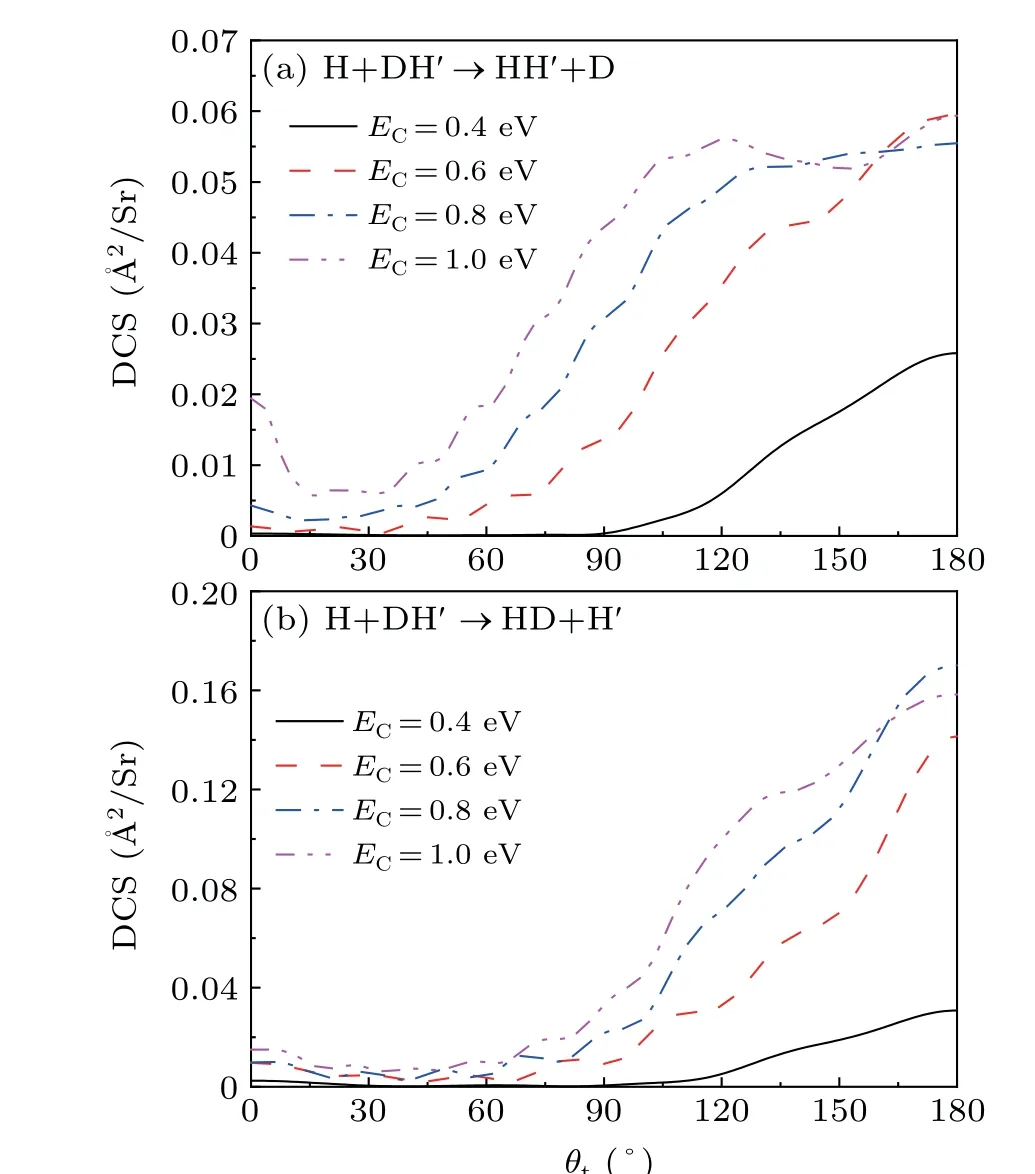
Fig.8. Total DCSs for(a)H+DH′→HH′+D and(b)H+DH′→HD+H′reactions at four collision energies.

The individual state-to-state DCS reveals more angular structures than the total DCS. Figures 9 and 10 show the state-resolved DCSs of H+DH′→HH′(v′=0,j′)+D and H+DH′→HD(v′= 0,j′)+H′reaction channels, respectively. It can be seen from the two figures that the products of the two channels present backward scattering distribution,especially for the small collision energy, the scattering angle is mainly concentrated at 180°. However, with the increase of the collision energy, the rotational quantum number of the product molecule becomes larger and larger,and the range of scattering angle gradually expands in the direction of decreasing.

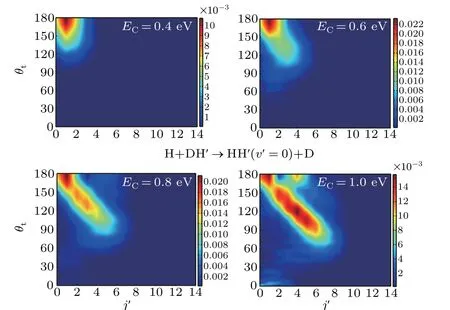
Fig. 9. The state-to-state DCS for H+DH′(v = 0,j = 0) →HH′(v′ =0,j′)+D reaction at four collision energies.

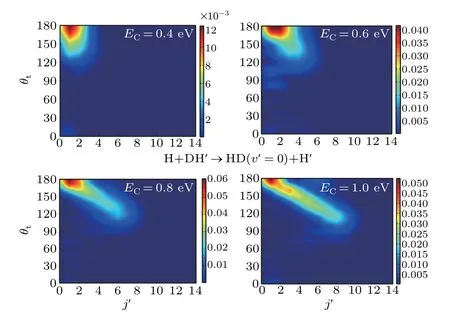
Fig. 10. The same as Fig. 9 but for H+DH′(v = 0,j = 0) →HD(v′ =0,j′)+H′ reaction at four collision energies.

In addition, there are some differences between the results of H+DH′→HH′+D and H+DH′→HD+H′channels. With the increase of the collision energy, the scattering angle of HH′molecules decreases more rapidly. Moreover,at the collision energy of 1.0 eV, HH′molecules with large rotational quantum number tend to have a more obvious sideway scattering distribution than that of HD, and the forward scattering HH′molecules begin appear. This forward scattering is more obvious in the state-resolved DCSs of the product molecule withv′=1,as shown in Fig.11. It was further verified that the contribution of the direct abstraction mechanism in the HH′product channel is greater than that in the HD channel at the higher collision energy. Moreover, HH′molecules withv′= 0 and 1 both contribute to the forward scattering component.

Fig.11. The state-to-state DCSs for(a)H+DH′(v=0,j=0)→HH′(v′ =1,j′)+D and(b)H+DH′(v=0,j=0)→HD(v′ =1,j′)+H′ reactions at the collision energy of EC=0.8 eV and 1.0 eV.

4. Summary

In this work,an efficient GPUs version of time-dependent wave-packet code has been used to calculate the differential cross section of H+DH′→HH′+D/HD+H′reactions on BKMP2 surface.

(i)There is a barrier in MEP,H+DH′→HH′+D/HD+H′reactions have threshold energy about 0.35 eV, which is lower than the barrier because of quantum tunnel.

(ii)By comparing with the earlier theoretical and experimental results of rotational state-resolved ICS of H+DH′→HH′+D reaction at the collision energy of 0.5 eV, it can be seen that our theoretical calculation results are closer to the experimental values forj′=1,2,4, so, to some extent, our calculation accuracy is higher.

(iii) The opacity functions are smoothly varied and exhibit arch shapes, largerJpartial waves are involved in the H+DH′→HH′+D channel and the bigger contributor to the H+DH′→HD+H′channel is the smallJ, according to the classical items, the direct abstraction mechanism is more dominant in H+DH′→HH′+D channel than H+DH′→HD+H′.

(iv)Because of the smaller gap of rotational energy level of the HD molecule, the maximum rotational energy level of HD product molecule can achieve is larger than HH′.

(v) Although both reaction channels are predominantly backward scattered due to the rebound mechanism,the contribution of direct abstraction reaction mechanism will increase at the high collision energies, and the forward scattering distribution of HH′is more obvious than that of HD.

All those show that the mass difference of isotopes can lead to a lot of differences in dynamics. Therefore, it is of great significance to study the isotopic effect on the dynamical properties.

Acknowledgment

The authors are very grateful to Prof. Han for providing he code.