Bilayer twisting as a mean to isolate connected flat bands in a kagome lattice through Wigner crystallization*
Jing Wu(吳靜) Yue-E Xie(謝月娥) Ming-Xing Chen(陳明星) Jia-Ren Yuan(袁加仁)Xiao-Hong Yan(顏曉紅) Sheng-Bai Zhang(張繩百) and Yuan-Ping Chen(陳元平)
1School of Physics and Optoelectronics,Xiangtan University,Xiangtan 411105,China
2Faculty of Science,Jiangsu University,Zhenjiang 212013,China
3School of Physics and Electronics,Hunan Normal University,Changsha 410081,China
4Department of Physics,Applied Physics,and Astronomy Rensselaer Polytechnic Institute,Troy,New York 12180,USA
Keywords: twisted bilayer kagome graphene,flat bands,Wigner crystallization
While graphene is known for its Dirac-like band structure near which electrons can move exceptionally fast with velocities on the order of 106m/s,[1-3]recently a new and opposite type of electronic behavior in graphene emerges. In a twisted bilayer graphene (TBG), due to the formation a long-range ordered moir′e pattern,[4-6]these fast electrons are no longer delocalized, but instead completely localized forming a Mott insulator and subsequently a superconductor.[7-22]Xieet al.proposed that such a superconducting behavior is originated from strong interactions of the electrons in the flat bands.[23,24]Shiet al.showed that there exists an intrinsic pseudo-magnetic field in the TBGs, which is tuned by the twisting angle.[25]These findings have attracted further attention to study the TBGs. For example,the twist angle can now be precisely controlled in experiment.Raman spectroscopy and Scanning electron microscope(SEM)techniques have been applied to identify the physical properties of the TBGs.[26-32]Theoretical calculations and analyses have also been carried out. Except for the electronic “magic” angle in 2D thin films like TBGs and twisted bilayer boron nitride(TBNN),[33]there exists photonic“magic”angle in twisted bilayerα-MoO3,making its topological polaritons transition controlled via twist angles.[34]As a matter of fact,the study of twisted bilayers has quickly moved beyond graphene,leading to the dawn of“twistronics”.[35-37]
Besides graphene, there are other two-dimensional (2D)carbon structures in the literature, such as T-, Pha-, and TPH-graphene,[38-41]as well as kagome graphene(KG).[42,43]While starting as theoretical predictions, some of the structures have been experimentally synthesized.[41]For having a distinct topology, they exhibit a rich variety of electronic properties,which are often completely different from those of graphene. For example, the KG is a carbon allotrope made of triangular carbon rings, as shown in Fig. 1(a). There exists a flat band that touches the Fermi level. A partiallyoccupied flat band is expected to host a range of exotic physical phenomena such as ferromagnetism,[44-46]Wigner crystallization,[47-50]anomalous quantum Hall effect,[51,52]and superconductivity.[7,53,54]
Unfortunately, however, the flat band of KG is not isolated,while isolation is a prerequisite for a number of important applications.[55-57]Instead, it contacts with other dispersive energy bands at a point in the Brillouin zone(BZ)known as the quadratic touching. To isolate the flat band from the other bands, one possible approach is to dope the system. At a precise filling of the flat band with a partial filling factor of 1/6, the band becomes isolated, leading to the formation of a Wigner crystal of electrons.[58]At a smaller filling, superconductivity may be expected also. For practical applications,the isolated flat band also must be robust. Hence, question arises: how to isolate the flat band(s) in a KG without the precision doping. It is important to note that the issue with quadratic touching is not KG specific. Rather, it is a general feature of the kagome lattice, regardless the underlying materials. Hence, how to isolate the flat band addresses a major challenge in the development and utilization of all kagome structures.
In this work, we propose that an isolation of the flat band(s) can be achieved by forming a twisted bilayer, based on first-principle density functional theory(DFT)calculations.The KG has a similar crystal symmetry with graphene.Hence,depending on the twisting angleθ, various moir′e superlattices can be generated in twisted bilayer kagome graphene(TBKGs), similar to those in graphene. Unlike the graphene,however, at a relatively large twisting angle (20° <θ <30°)and hence in a relatively small moir′e superlattice,isolated flat bands already formed. Based on the DFT results, a tightbinding (TB) model is constructed to study the isolated flat bands at smallerθ(<10°). All the flat bands are topological nontrivial. Importantly,each isolated flat band corresponds to having a unique pattern of the Wigner crystal in real space,andvice versa. Hence, Wigner crystallization of electrons is the reason for the isolation of the flat bands. Because the bands start to be flat in a kagome lattice, any finite and periodic perturbation (large than the band width) is enough to cause a spontaneous crystallization,which is fulfilled and realized here by the van der Waals(vdW)interaction of the moir′e superlattice between layers.

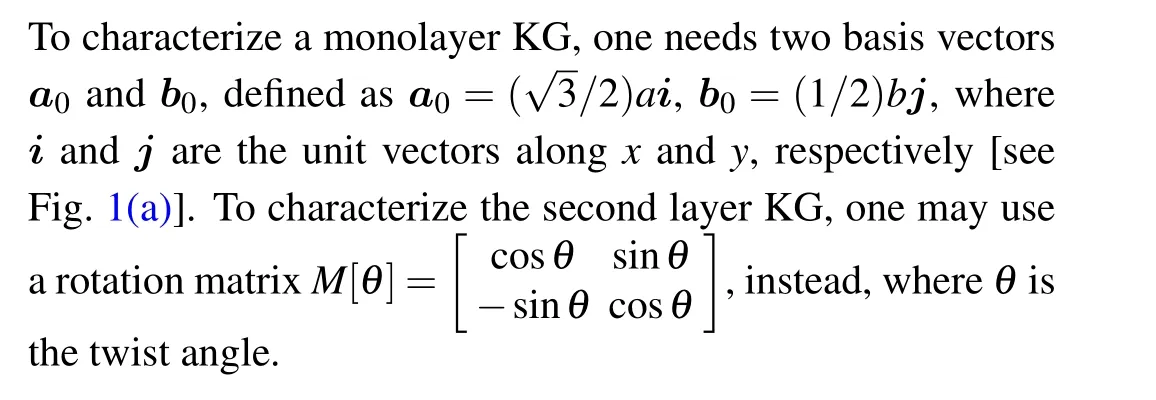
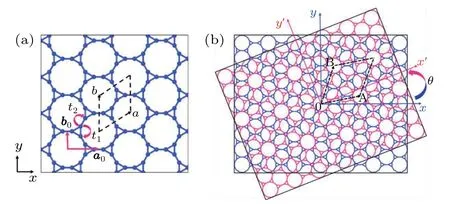
Fig.1. (a)Monolayer KG,made of triangular carbon rings. Dashed rhombus indicates the primitive cell for which the lattice constants are a and b,the basis vectors are a0 and b0, and the intra-layer hopping parameters are t1 and t2.(b)A schematic view of the TBKG,in which the pink layer is twisted with respect to the blue one underneath by an angle θ around the common origin(labeled in the figure as 0). Dashed rhombus indicates the supercell (= the primitive cell of TBKG)for which the lattice constants are A and B.
Asθchanges, different moir′e superlattices are formed.One can also use a pair of integers (m,n) to define the twist angleθ,namely,angleθin the range of 0°to 30°.[59,60]

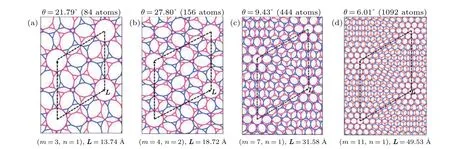
Fig. 2. Schematic illustrations of TBKGs with (a) θ =21.79°, (b) θ =27.80°, (c) θ =9.43°, and (d) θ =6.01° . Dashed rhombuses are the primitive cells for the moir′e superlattices. At the bottom of each panel,indices(m,n)are given,which are related to twisting angle θ via Eq.(1). L is the dimension of the primitive cell.
Our calculations were performed within DFT as implemented within the Perdew-Burke-Ernzerhof (PBE) approximation to the exchange-correlation functional. The corevalence interactions were described by the projector augmented wave (PAW) potentials, as carried out in the Vienna ab initio simulation package (VASP). Plane waves with a kinetic energy cutoff of 500 eV were used as the basis set. The Monkhorst-Pack scheme was used to sample the BZ integration. For TBKG withθ=21.79°(TBKG21.79°)and 27.80°(TBKG27.80°),a 3×3×1k-point mesh was used.The atomic positions were fully relaxed by the conjugate gradient method.The energy and force convergence criteria were 10-5eV and 10-3eV/?A, respectively. To avoid interaction between adjacent layers,a vacuum slab of 18-?A thick was used to separate the bilayers. The Grimme-D3 correction was used to account for van der Waals interactions.[61,62]
Figures 3(a)-3(b)show the band structures of monolayer KG and bilayer KG with the AA stacking,respectively. In the monolayer case,there is a flat band just below the Fermi level,which contacts quadratically with another band atΓpoint of the BZ [see Fig. 3(a)]. As shown previously, upon a partial hole doping, ferromagnetism and Wigner crystallization can be realized.For the AA-stacked bilayer KG,on the other hand,figure 3(b) shows two sets of similar energy bands near the Femi level.The splitting between the two flat bands is approximately 1.0 eV,which indicates that van der Waals interactions between layers have a significant effect on the electronic structure,although their effects on the interlayer cohesion is small.Despite the large splitting,however,both flat bands remain in contact with neighboring bands.

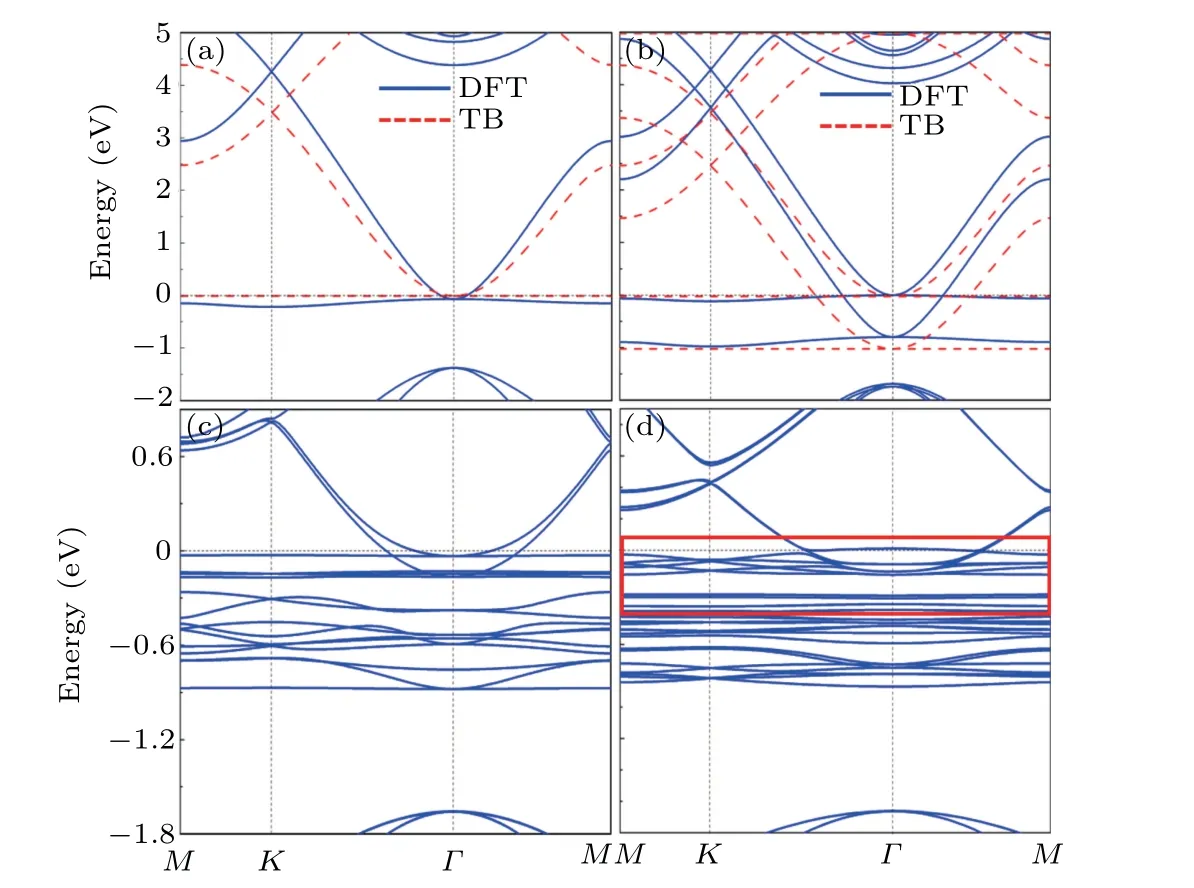
Fig. 3. Band structures of (a) monolayer KG, (b) AA-stacked bilayer,(c) TBKG21.79°, and (d) TBKG27.80°. In panels (a) and (b), solid blue lines are the DFT results, whereas dashed red lines are the TB model. See Eq.(2). The red frame in panel(d)is enlarged as shown in Fig.4(a).

As mentioned earlier, a Wigner crystallization can lead to an isolated flat band. However, such a crystallization does not spontaneously happen unless the relevant flat band is at the Fermi level and can be doped controllably. In contrast,the flat bands here are not exactly at the Fermi level,although for application purposes being at the Fermi level can be advantageous. Fractional doping is also un-attempted here. The results in Fig.4(a)thus suggest that fractional doping is not the only way to produce a Wigner crystal. Interactions between the bilayers here,despite being relatively weak,can also be an effective means to produce the Wigner crystal. To show that indeed the formation of isolated flat bands in Fig.3(d)is a direct result of the Wigner crystallization,we plot in Fig.4(b)the charge densities corresponding to the two flat bands, namely,band 1 and band 2. In both cases,as a hallmark of the Wigner crystallization (driven by repulsion between electrons), the charges confine themselves inside isolated rings,which in turn form a regular triangular lattice. We can also see the charge density states detailedly in Fig.S1 from the supplementary informations (SI). It shows that the electrons charge localized as hexagonal rings in every twisted layer. A nd there is no similar phenomena in single layer kagome graphene and AAstacked structure in Fig. S2 in SI. It happens regardless the atomic structure and symmetry of the crystal. We therefore conclude that bilayer twisting is an effective way to produce isolated flat bands via a spontaneous Wigner crystallization.Here,we stress the word“spontaneous”because the isolation of the flat bands takes place in a twisted bilayer even without any atomic relaxation.

Fig. 4. (a) Enlarged band structure within the red frame in Fig. 3(d). Two isolated flat bands are labeled as 1 and 2, respectively. (b)Charge densities corresponding to band 1 and 2 in panel(a). Both involve enclosed circles but with different radii.
Before moving on, we would like to point out that for TBKG21.79°, in theory a spontaneous Wigner crystallization can also take place. However, it happens that the relevant flat bands are above the quadratically-touched flat band [see Fig.3(c)]. The crossing with the dispersed band renders them not very useful. In terms of charge localization, while it can happen atk-points away from the crossing points, the band mixing at and near the crossing points ruins the possibility of having a complete Wigner crystallization.
Next, we consider TBKGs with even smallerθ(<10°).Here the large supercell size makes it impractical to perform DFT calculations. Instead, we use the tight-binding model.OnlyPzorbitals of the carbon atoms contribute to the electronic structure near the Fermi level. Hence, we can use the following Hamiltonian for TBKGs:is the interlayer interaction,and

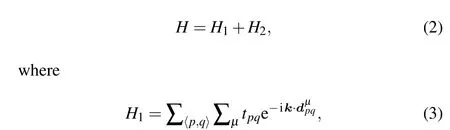
Figure 5(a) shows the band structure forθ= 6.01°.A smaller angle typically corresponds to a larger supercell,which leads to more BZ folding and, as such, more isolated flat bands. For example,see band 1 in Fig.5(a)and bands 2 to 5 in the zoomed-in plot in Fig. 5(b), which is over an energy range of merely 0.15 eV(between-0.78 eV and-0.63 eV).It is interesting to note that with a smaller twisting angle, the flat bands become so flat that the dispersion is negligible over the entire BZ.Charge densities for the five selected bands are shown in Fig.5(c),all of which form triangular Wigner crystals.Despite that all the localized electrons are confined within closed rings,the radii of the rings can be different:e.g.,bands 1 to 3 have smaller radii,while bands 4 and 5 have larger radii.In general, the tighter the radius, the less the energy dispersion. In addition to the isolated flat bands, non-isolated flat bands are also found. Fig. S5 in SI depicts charge distributions for some of them. In startle contrast to the isolated flat bands, however, none of the non-isolated ones show sign of Wigner localization.
Fig. 5. (a) Band structure of TBKG6.01°, based on the TB model in Eq.(2).The parametersusedinthecalculation aret1=-3eV,t2=-6eV,Vp0pπ =-3 eV,Vp0pσ =-0.50eV,and δ =0.184a.(b)Enlarged band structure corresponding to the green frame at the bottom of panel (a). A subset of isolated flat bands in panels (a) and (b) are selectively labeled as 1 to 5.(c)The corresponding charge-density patterns. All show Wigner crystallization.
Note that a twist operation here not only reduces the symmetry of the crystal but also cause a reconstruction of the atomic structure due to interlayer interaction.To see its effects on the atomic structure,Table 1 compares cohesive energy,interlayer spacing, and bond length for several typical stacking sequences which are AA, AA′, and AB (or equivalently BA)and twisting (given by DFT). The perfect stacking structures are shown in Fig.S6 in SI.
The cohesive energies of the stacked structures are as follows:AA′has the lowest energy; AB is next, while AA has the highest energy. All are lower than that of monolayer KG,indicating that stacking is energetically favored. It happens that TBKG21.79°and TBKG27.80°have the same energies as the AA and AB stacking, respectively. There are two different bond lengths for monolayer KG of 1.353 and 1.424 ?A.They are little change upon forming the bilayers and twisting, on average, within (-0.0, +0.4)% for the shorter bond and(-0.2,+0.1)%for the longer bond. The general trend is that the shorter ones slightly elongate while the longer ones slightly shrink.
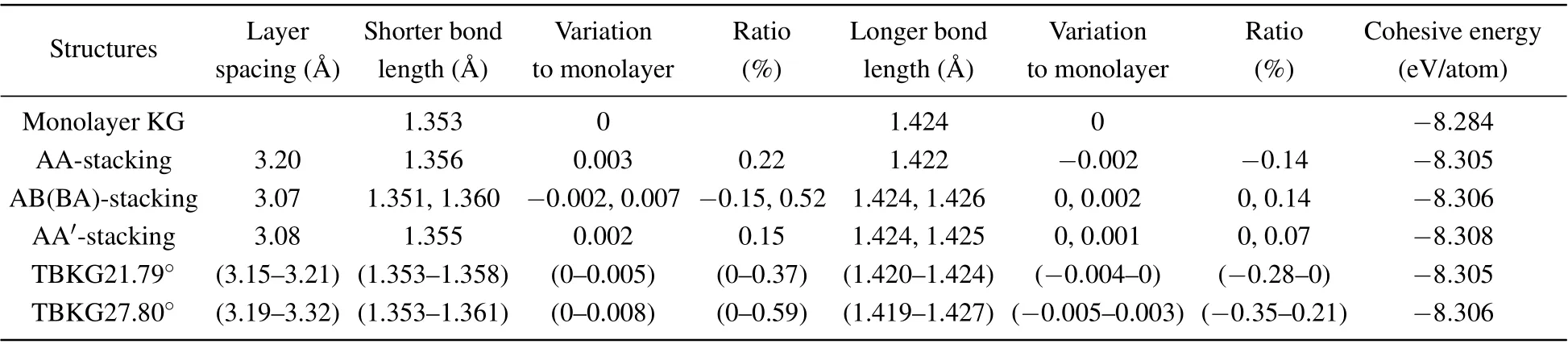
Table 1. Calculated layer spacing,bond length,and cohesive energy for various atomic structures.
The interlayer spacing, on the other hand, is changed considerably. For example, the spacing for the AA-stacking isdAA=3.20 ?A, which should be contrasted with those for the AA′-stacking (dAA′=3.08 ?A) and AB-stacking (dAB=3.07 ?A).The ratio of(dAA-AA′/d′AA)=3.9%,which is an order of magnitude larger than the changes in the bondlength≤0.4%.A twist generally causes additional corrugation in the interlayer spacing:e.g., for TBKG21.79°, the spacing varies between 3.15 ?A and 3.21 ?A with a spread of Δd=0.06 ?A;for TBKG27.80°, it varies between 3.19 ?A and 3.32 ?A with a spread of Δd=0.13 ?A. Also, it is interesting to note that both interlayer spacings here are closer to that of AA-stacking,although energetically TBKG27.80°is the same as the ABstacking.
Using kagome graphene as an example,we show by DFT and TB calculations that flat band isolation can be achieved by a moir′e potential,coreated via twisting a double layer. At relatively large twisting angles(20°<θ <30°),the potential,which is vdW in nature, is already strong enough to isolate the flat band. This is qualitatively different from the twisted bilayer graphene where the reduction of the kinetic energy to be comparable to the interlayer vdW potential requires much larger supercells and hence much smaller twisting angles. All the isolated flat bands are topological nontrivial.[67-69]The physical origin for the flat band isolation is rooted in the Wigner crystallization. As a flat band possesses a number of intriguing physical properties such as ferromagnetism,anomalous quantum hall effect, and superconducting, it should be interesting to explore the interplay between these effects and Wigner crystallization.
- Chinese Physics B的其它文章
- Projective representation of D6 group in twisted bilayer graphene*
- Magnon bands in twisted bilayer honeycomb quantum magnets*
- Faraday rotations,ellipticity,and circular dichroism in magneto-optical spectrum of moir′e superlattices*
- Nonlocal advantage of quantum coherence and entanglement of two spins under intrinsic decoherence*
- Universal quantum control based on parametric modulation in superconducting circuits*
- Universal quantum circuit evaluation on encrypted data using probabilistic quantum homomorphic encryption scheme*

