裝飾根森林上的自由余圈無窮小單位Hopf 代數(shù)
張毅 曹靖涵 吳笑醒
(南京信息工程大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,南京,210044)
1 Introduction

The concept of infinitesimal bialgebras may be found in study of the calculus of Newton divided differences which was first introduced by Joni and Rota[23]. The main difference between infinitesimal bialgebras and classical bialgebras is that the coproduct of infinitesimal bialgebras is a derivation rather than an algebra homomorphism. Namely,an infinitesimal bialgebra is a moduleA,which is simultaneously an algebra(possibly without a unit)and a coalgebra(possibly without a counit),such that the coproduct Δ is a derivation:When an infinitesimal bialgebra has an antipodeS,it is called an infinitesimal Hopf algebra[1]. The basic theory of infinitesimal bialgebras and infinitesimal Hopf algebras was originally established in[1,2,3].Apparently,infinitesimal bialgebras remained uncontested until 2009,when new motivations were found,coming on one hand from interesting applications to combinatorics[15],and on the other hand from the close relation to the operad[16]. In 2010, Bai[4]studied antisymmetric infinitesimal bialgebras, which have a close connection with dendriform D bialgebras, Frobenius algebras, and O operators [4, 5, 6].Later,Wang and Wang[31]generalized Aguiar’s result by the name of braided infinitesimal Hopf algebras in Yetter Drinfeld categories, and Yau [32] introduced infinitesimal Hom bialgebras which were further studied by Liu,Makhlouf,Menini and Panaite[26]. Ma and Yang[28]investigated the Drinfeld double for infinitesimal BiHom bialgebras.
The rooted forest is an important object studied in algebraic combinatorics. The well known Connes Kreimer Hopf algebra[8]was constructed on rooted forests, which was used to treat a problem of Renormalisation in Quantum Field Theory [8, 12, 20, 24]. Along with the line of Connes Kreimer’s work,researchers constructed many other Hopf algebras on rooted forests,such as Grossman Larson Hopf algebras [17], Loday Ranco Hopf algebras [27] and Foissy Holtkamp Hopf algebras [14, 22]. These algebraic structures are important because all of them have universal properties, which have interesting applications in renormalization[29].
The concept of operated algebras was first introduced by Higgins [21] on multi operator group in 1956. After that,Kurosh[25]proposed the notation of algebras with(one or more)linear operators,which was forgotten almost 50 years until it was rediscovered by Guo[19]. Guo called it an Ω operated algebra and constructed the free Ω operated algebra on a set,where Ω is a nonempty set used to index the operators.See also[7].
Recently the discovery of some new algebraic structures in mathematics and mathematical physics has led to a renewed interest in the study of Ω operated algebras and their free objects. For example,the Connes Kreimer Hopf algebras [9] of rooted forests equipped with a family of grafting operations is an Ω operated algebra. Viewing Hopf algebras in the framework of operated algebras, Zhang, Gao and Guo[33]proposed the concept of cocycle Hopf algebras,when a Hochschild 1 cocycle condition is involved. An operated algebra approach of Loday Ronco Hopf algebras was investigated in[35]in terms of decorated planar binary trees.
In [36], Zhang and Gao constructed an infinitesimal bialgebras on decorated rooted forests and combine it with operated algebras. In this paper,we equip this infinitesimal bialgebras with an antipode such that it is further an infinitesimal unitary Hopf algebra. We also conceptualize the mixture of operated algebras and infinitesimal unitary Hopf algebras,and characterize freeness of cocycle infinitesimal unitary Hopf algebras in such categories.
Notation. Throughout this paper,letkbe a unitary commutative ring unless the contrary is specified,which will be the base ring of all modules, algebras, coalgebras, bialgebras, tensor products, as well as linear maps. By an algebra we mean an associative algebra(possibly without unit)and by an coalgebra we mean a coassociative coalgebra(possibly without counit). We use the Sweedler notation:

For an algebraA,A ?Ais viewed as anAbimodule in the standard way
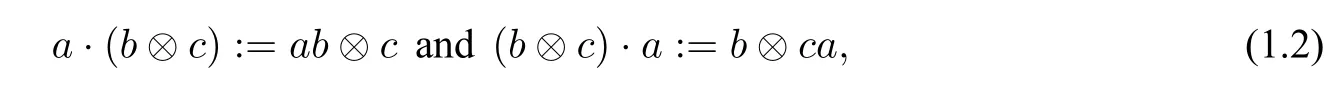
wherea,b,c ∈A.
2 Infinitesimal bialgebras and infinitesimal Hopf algebras
In this section, we first recall the concepts of infinitesimal bialgebras and infinitesimal Hopf algebras[11].
2.1 Infinitesimal bialgebras
Definition 2.1(a) An infinitesimal bialgebra (abbreviated?bialgebra) is a triple (A,m,Δ)consisting of an algebra(A,m)and a coalgebra(A,Δ)that satisfies

(b) If further (A,m,1) is a unitary algebra, then the quadruple (A,m,1,Δ) is called an infinitesimal unitary bialgebra.
(c) If further(A,Δ,ε)is a counitary coalgebra,then the quadruple(A,m,Δ,ε)is called an infinitesimal counitary bialgebra.
Remark 2.1(a) Let(A,m,1,Δ)be an?unitary bialgebra. Then Δ(1)=0,as

(b) Let (A,m,1,Δ) be an?unitary bialgebra. Define a linear mapd:A →Aby takingd:=mΔ.
Thendis a derivation,that is
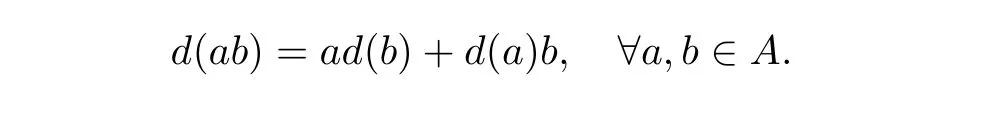
(c) Let(A,m,1,Δ)be an?bialgebra. Define
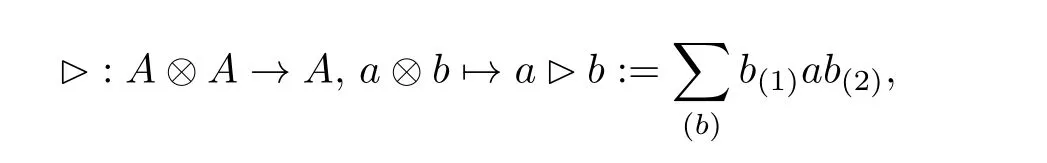
whereb(1),b(2)are from the Sweedler notation Δ(b)=(b)b(1)?b(2). Then(A,?)is a pre Lie algebra.(d) Aguiar[1]showed that there is no a nontrivial?bialgebra both having a unit and a counit. Indeed,it follows the counicity that
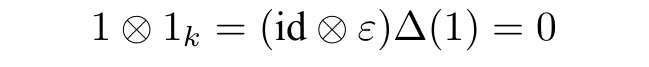
and so 1=0.
Definition 2.2LetAandBbe two?bialgebras. A mapφ:A →Bis called an infinitesimal bialgebra morphism ifφis an algebra morphism and a coalgebra morphism. The concept of an infinitesimal unitary bialgebra morphism can be defined in the same way.
Example 2.1Here are some examples of weighted?unitary bialgebras.
(a)[1,example 2.3.5] The polynomial algebrak〈x1,x2,x3,···〉is an?bialgebra with the coproduct Δ given by Eq.(2.3)and
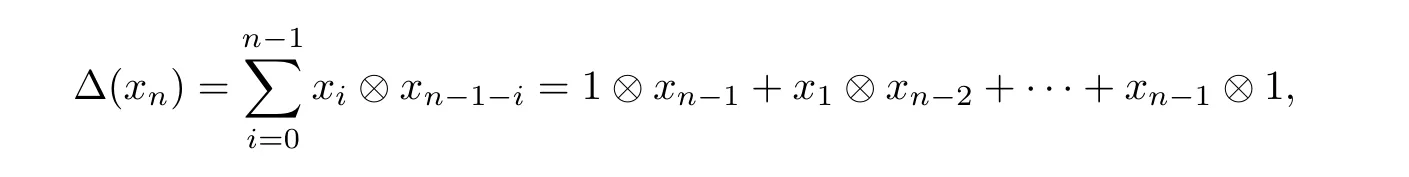
where we setx0=1. Indeed it is further an?unitary bialgebra.
(b)[1,example 2.3.2] A quiverQ=(Q0,Q1,s,t)is a quadruple consisting of a setQ0of vertices,a setQ1of arrows,and two mapss,t:Q1→Q0which associate each arrowa ∈Q1to its sources(a)∈Q0and its targett(a)∈Q0. The path algebrakQcan be turned into an?bialgebra of weight zero with the coproduct Δ given by:
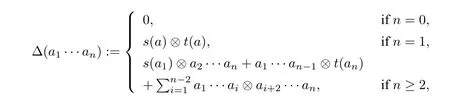
wherea1···anis a path inkQ. Here we use the convention thata1···an ∈Q0whenn=0.
2.2 Infinitesimal unitary Hopf algebras
We denote by Homk(A,B) the space of linear maps fromAtoB. LetH= (H,m,1,Δ,ε) be a classical bialgebra. Iff,g ∈Homk(H,H),their convolution is the mapf ?g:H →Hdefined to be the composition:
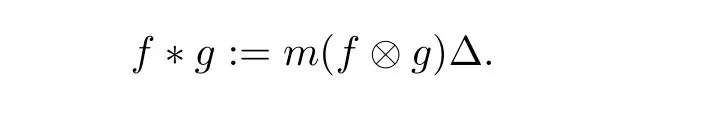
Note that 1?εis the unit with respect to?. The antipodeSis defined to be the inverse of the identity map with respect to the convolution product[10,Chapter 4.1].
It is almost a natural question to wonder whether we can define the antipode for?bialgebrasHas one did for classical bialgebras. Aguiar gave a negative answer for this question, due to the lack of the unit 1?εwith respect to?,see Remark 2.2 (d)for more details. In order to fill this gap for?bialgebras,Aguiar[1]equipped Homk(H,H)with a circular convolution ?defined by
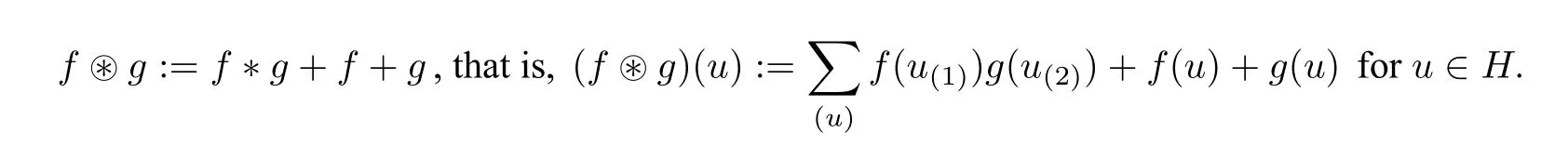
Note thatf?0=f=0 ?fand so 0∈Homk(H,H)is the unit with respect to the circular convolution?. Then Aguiar introduced the concept of?Hopf algebras in the following.
Definition 2.3([1, Definition 3.1]) An?bialgebra (H,m,Δ) is called an infinitesimal Hopf algebra(abbreviated?bialgebra)if the identity map id∈Homk(H,H)is invertible with respect to the circular convolution ?. In this case,the inverseS ∈Homk(H,H)of id is called the antipode ofH. It is characterized by
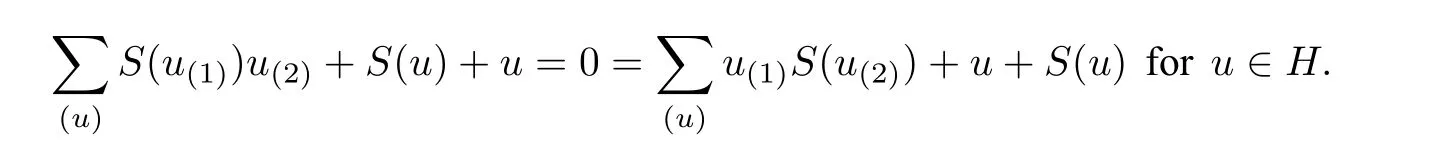
If(H,m,1)is a unitary algebra,thenHis called an infinitesimal unitary Hopf algebra.
The?Hopf algebra also satisfies some properties analogous to those of a classical Hopf algebra.
Remark 2.2([1,Propositions 3.7,3.12]) (a) LetAbe an?Hopf algebra with antipodeS. Then
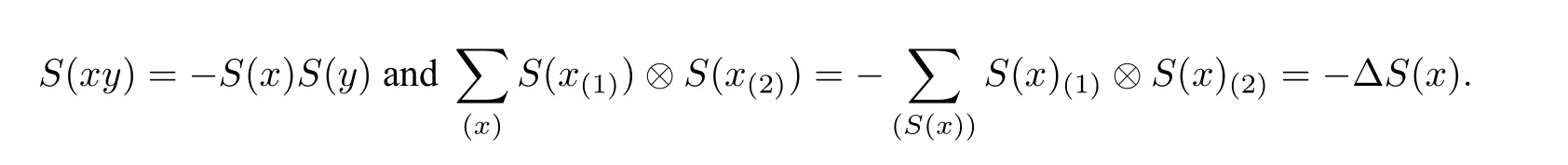
(b) If(A,m,1,Δ)is an?Hopf algebra with the antipodeS,then so is(A,mop,1,Δcop)with the same antipodeS.
Definition 2.4Let(H,mH,ΔH)and(H′,mH′,ΔH′)be two?Hopf algebras and letSH,SH′be the antipodes ofH,H′,respectively. An?bialgebra morphismφ:H →H′is called an?Hopf algebra morphism if it satisfies the condition
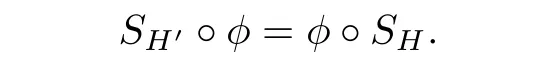
The concept of an?unitary Hopf algebra morphism can be defined in the same way.
Example 2.2We adapt from [1, example 3.2] to expose the following example. The?unitary bialgebrak〈x1,x2,x3,···〉in example 2.1 is an?unitary Hopf algebra with the antipode
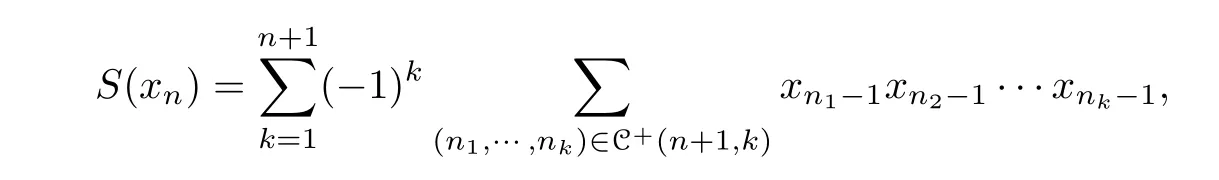
where C+(n+1,k)={(n1,··· ,nk)|ni ∈Z+,n1+···+nk=n+1}is the set of strict compositions ofn+1 intokparts.
3 Infinitesimal unitary Hopf algebras of rooted forests
In this section, we first recall the concepts of planar rooted trees [30] and decorated planar rooted forests[14,19,34,33]. We then prove that the infinitesimal unitary bialgebra on decorated rooted forests constructed in[36]can be further an infinitesimal unitary Hopf algebra.
3.1 Decorated planar rooted forests
Definition 3.1([18,30]) A rooted tree is a finite graph,connected and without cycles,with a special vertex called the root. A planar rooted tree is a rooted tree with a fixed embedding into the plane.
The following are some planar rooted trees.

where the root is on the bottom of a tree[30]. Let T denote the set of planar rooted trees andM(T)the free monoid generated by T with the concatenation product, denoted bymRTand usually suppressed.The empty tree inM(T) is denoted by 1. An element inM(T), called a planar rooted forest, is a noncommutative concatenation of planar rooted trees, denoted byF=T1···TnwithT1,··· ,Tn ∈T.Whenn=0,we denoteFby 1. The following are few planar rooted forests:

Let T(X,Ω) (resp. F(X,Ω) :=M(T(X,Ω))) denote the set of planar rooted trees (resp. forests)whose internal vertices are decorated by elements of Ω exclusively and leaf vertices are decorated by elements ofΩ. Every element of F(X,Ω)is called a decorated planar rooted forest. If a tree has only one vertex,the vertex is treated as a leaf vertex. Here are some examples in F(X,Ω):
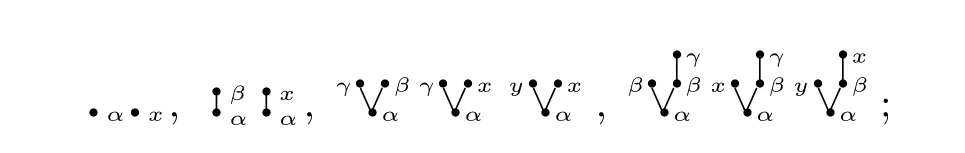
whereas,the following is an example not in F(X,Ω):

wherex,y ∈Xandα,β,γ ∈Ω.
Denote by
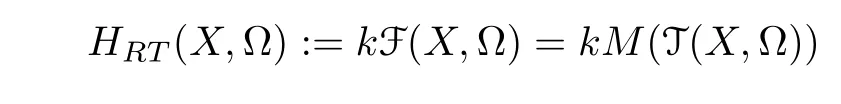
the freekmodule spanned by F(X,Ω). For eachω ∈Ω,define
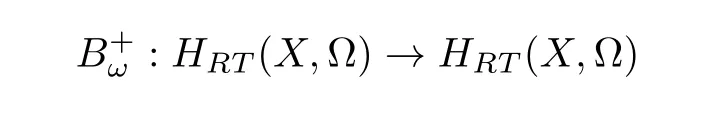
to be the linear grafting operation by taking 1 to?ωand sending a rooted forest inHRT(X,Ω)to its grafting with the new root decorated byω. For example,
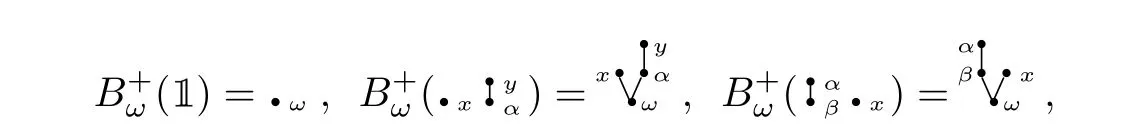
whereα,β,ω ∈Ω andx,y ∈X. Note thatHRT(X,Ω)is closed under the concatenationmRT.
ForF=T1···Tn ∈F(X,Ω)withn ≥0 andT1,··· ,Tn ∈T(X,Ω),we define bre(F):=nto be the breadth ofF. Here we use the convention that bre(1)=0 whenn=0. In order to define the depth of a decorated planar rooted forest,we build a recursive structure on F(X,Ω). Denote?X:={?x|x ∈X}and set
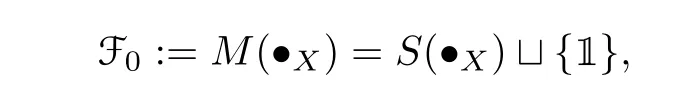
whereM(?X)(resp.S(?X))is the submonoid(resp.subsemigroup)of F(X,Ω)generated by?X. Here we are abusing notion slightly sinceM(?X) (resp.S(?X)) is also isomorphic to the free monoid (resp.semigroup)generated by?X. Suppose that Fnhas been defined for ann ≥0,then define
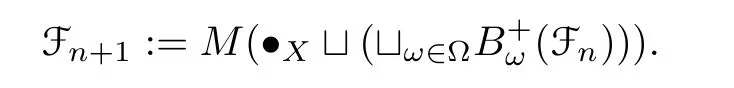
Thus we obtain Fn ?Fn+1and
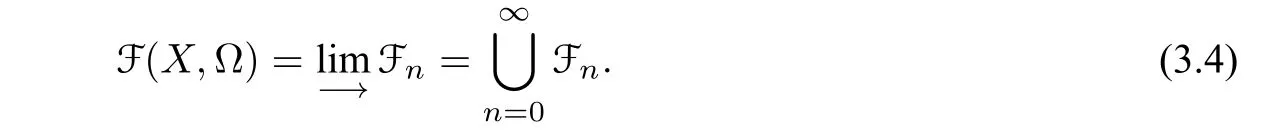
Now elementsF ∈FnFn?1are said to have depthn,denoted by dep(F)=n. The following are some examples:

3.2 The construction of a coproduct on decorated planar rooted forests
In this subsection,we recall the construct of the coproduct Δ?from [36],which makes it possible to give an?unitary bialgebra onHRT(X,Ω).
It suffices to define Δ?(F)for basis elementsF ∈F(X,Ω)by induction on dep(F). For the initial step of dep(F)=0,we define

Here in the third case,the definition of Δ?reduces to the induction on breadth and the left and right actions are given in Eq.(1.2).
For the induction step of dep(F)≥1,we reduce the definition to induction on breadth. If bre(F)=1,we writeF=for someω ∈Ω andF(X,Ω),and define
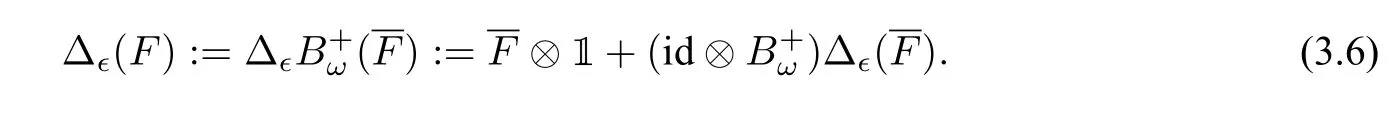
In other words,

Eq.(3.6)or equivalently Eq.(3.7)is called the infinitesimal 1 cocycle condition[36]. If bre(F)≥2,we writeF=T1T2···Tmfor somem ≥2 andT1,··· ,Tm ∈T(X,Ω),and define
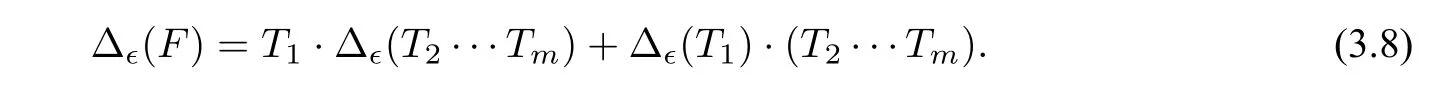
Let us expose some examples for better insight into Δ?.
Example 3.1Letx,y ∈Xandα,β,ω ∈Ω. Then
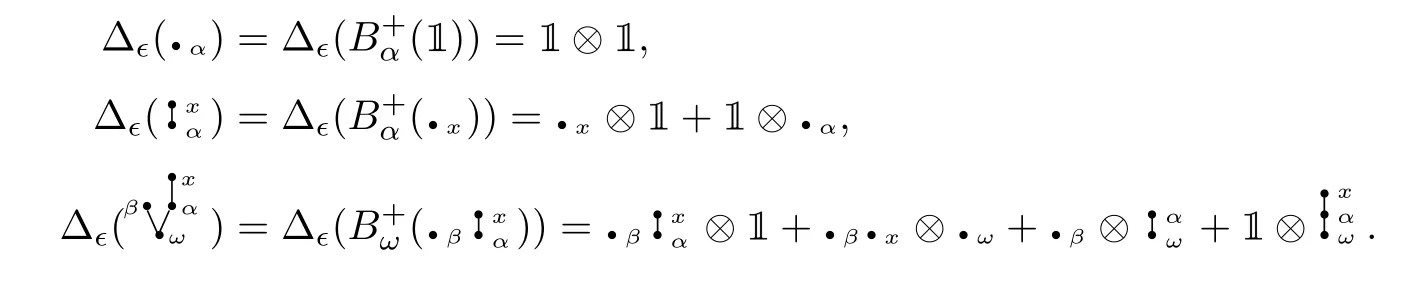
Proposition 3.1([36]) The quadruple(HRT(X,Ω), mRT,1,Δ?)is an?unitary bialgebra.
3.3 An infinitesimal unitary Hopf algebras on decorated planar rooted forests
In this subsection,we equip the?unitary bialgebraHRT(X,Ω)obtained in Proposition 3.1 with an antipode such that it is further an?unitary Hopf algebra.
Definition 3.2 ([1, Section 4]) LetAbe an algebra andCa coalgebra. The mapf:C →Ais called locally nilpotent with respect to the convolution?if for eachc ∈Cthere is somen ≥1 such that
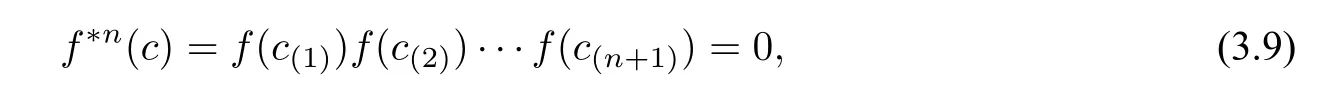
wherec(1),··· ,c(n+1)are from the Sweedler notation Δn(c)=?···?c(n+1).
Denote by R and C the field of real numbers and the field of complex numbers,respectively.
Lemma 3.1([1,Proposition 4.5]) Let(A, m,Δ)be an?bialgebra over a fieldkandD:=mΔ.Suppose that either(a)k=R or C andAis finite dimensional,or(b)Dis locally nilpotent and char(k)=0.
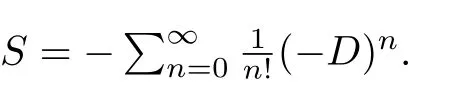
We proceed to prove thatmRTΔ?onHRT(X,Ω)is locally nilpotent. For this,denote by where|V(F)|is the number of vertices ofF.
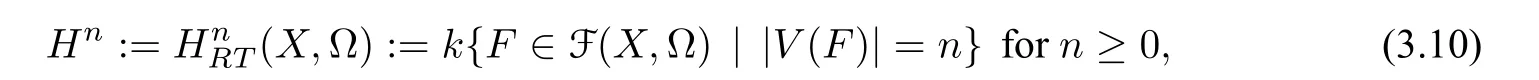
Lemma 3.2LetHnbe given in Eq.(3.10)andn ≥1. Then
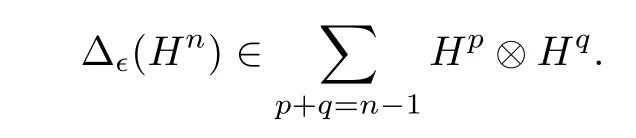
ProofIt is enough to show that
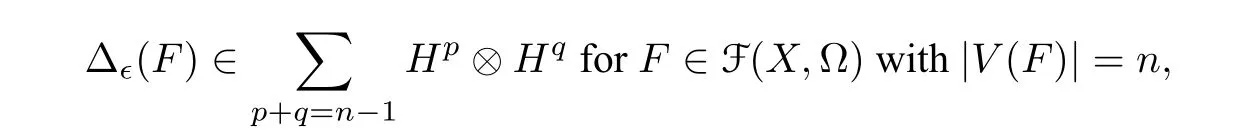
which will be proved by induction onn ≥1. Whenn=1,by Eq.(3.5)and Eq.(3.6),we have
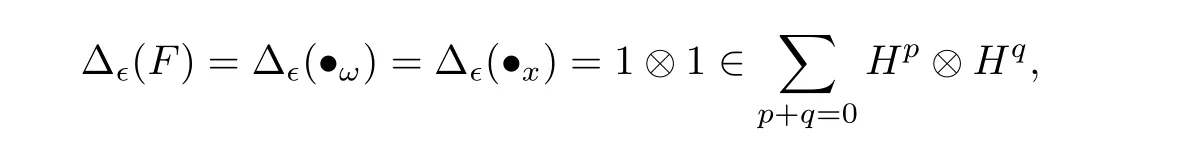
withω ∈Ω andx ∈X. Assume that the result holds forn Hence Assume that the result holds forn=mand bre(F) For eachi=1,··· ,k,by the induction hypothesis,we have and so by Eq.(1.2), Hence This completes the proof. Lemma 3.3Let(HRT(X,Ω), mRT,1,Δ?)be the?unitary bialgebra in Proposition 3.1 and Then for eachn ≥0 andF ∈Hn,D?(n+1)(F)=0 and soDis locally nilpotent. ProofIt suffices to prove the first statement by induction onn ≥0. For the initial step ofn=0,we haveF=1. It follows from Eqs.(3.5)and(3.9)that Assume that the result is true forn Case 1bre(F)=1. IfF=?xfor somex ∈X,then SupposeF ?=?xfor allx ∈X. ThenF=(F)for someω ∈Ω andF ∈Hk?1. Thus Here the last step employs the fact that|V(F(1))|<|V(F)|<|V(F)| =kby Lemma 3.2 and soD?k()=0 by the induction hypothesis. Case 2bre(F)≥2. Then we may writeF=F1F2with 0 It follows from Lemma 3.2 that and soD?k(F1F2(1)) = 0 by the induction hypothesis. Similarly,|V(F1(1))|<|V(F1)|<|V(F)| =kandD?k(F1(1))=0. ThusD?(k+1)(F)=0. This completes the proof. The following result shows thatHRT(X,Ω)has an?unitary Hopf algebraic structure. In this section,we study?unitary Hopf algebra in the framework of operated algebras,leading to the concept of cocycle?unitary Hopf algebras. We also show thatHRT(X,Ω)is the free Ω cocycle?unitary Hopf algebra on a setX. The concept of the algebra with(one or more)linear operators was introduced by Kurosh[25]. Later Guo[19]called it operated algebras and constructed free operated algebras on a set. See also[7,18]. Definition 4.1([19]) Let Ω be a nonempty set. (a) An Ω operated monoid is a monoidMtogether with a set of operatorsPω:M →M,ω ∈Ω.(b) An Ω operated (unitary) algebra is a (unitary) algebraAtogether with a set of linear operatorsPω:A →A,ω ∈Ω. Inspired by Eq.(3.6),we introduce the following concepts. Definition 4.2([36]) Let Ω be a nonempty set. (a) An Ω operated?bialgebra is an?bialgebraHtogether with a set of linear operatorsPω:H →H,ω ∈Ω. If furtherHhas a unit,thenHis called an Ω operated?unitary bialgebra. (b) Let (H, {Pω|ω ∈Ω}) and (H′, {|ω ∈Ω}) be two Ω operated?bialgebras. A linear mapφ:H →H′is called an Ω operated?bialgebra morphism ifφis a morphism of?bialgebras andφ?Pω=P′ω?φforω ∈Ω. The Ω operated?unitary bialgebra morphism can be defined in the same way. (c) An Ω cocycle?unitary bialgebra is an Ω operated?unitary bialgebra(H, m,1,Δ,{Pω|ω ∈Ω})satisfying the?cocycle condition: (d) The free Ω cocycle?unitary bialgebra on a setXis an Ω cocycle?unitary bialgebra(HX, mX,1X,ΔX, {Pω|ω ∈Ω}) together with a set mapjX:X →HXwith the property that,for any Ω cocycle?unitary bialgebra(H, m,1,Δ, {|ω ∈Ω})and any set mapf:X →Hsuch that Δ(f(x)) = 1?1 forx ∈X, there is a unique morphism ˉf:HX →Hof Ω operated?unitary bialgebras such that ˉf ?jX=f. When Ω is a singleton set, we will omit the “Ω”. The following result generalizes the universal properties studied in[9,13,19,29,33]. Recall from Eq.(3.4)that Theorem 4.1([36]) LetXbe a set andjX:F(X,Ω),?xthe natural embedding. Then the quintuple (HRT(X,Ω), mRT,1,Δ?, {|ω ∈Ω}) together with thejXis the free Ω cocycle?unitary bialgebra onX. In this subsection,we prove thatHRT(X,Ω)is the free Ω cocycle?unitary Hopf algebra on setX.The following concepts are motivated from Definitions 4.2 and 2.3. Definition 4.3Let Ω be a nonempty set. (a) An Ω operated?Hopf algebra is an?Hopf algebraHtogether with a set of linear operatorsPω:H →H,ω ∈Ω. If furtherHhas a unit,thenHis called an Ω operated?unitary Hopf algebra. (b) Let(H, {Pω|ω ∈Ω})and(H′, {|ω ∈Ω})be two Ω operated?Hopf algebras. A linear mapφ:H →H′is called an Ω operated?Hopf algebra morphism ifφis an?Hopf algebra morphism andφ ?Pω=?φforω ∈Ω. The Ω operated?unitary Hopf algebra morphism can be defined similarly.(c) An Ω cocycle?unitary bialgebra is called an Ω cocycle?unitary Hopf algebra if it is also an?unitary Hopf algebra. (d) The free Ω cocycle?unitary Hopf algebra on a setXis an Ω cocycle?unitary Hopf algebra(HX, mX,1X,ΔX, {Pω|ω ∈Ω}) together with a set mapjX:X →HXwith the property that,for any Ω cocycle?unitary Hopf algebra(H, m,1,Δ, {|ω ∈Ω})and any set mapf:X →Hsuch that Δ(f(x))=1?1 forx ∈X,there is a unique morphism ˉf:HX →Hof Ω operated?unitary Hopf algebras such that When Ω is a singleton set, we shall omit “Ω” in the above notations. As the well known result in classical Hopf algebras,Aguiar showed that Lemma 4.1([1, Proposition 3.8]) LetHandH′be two?Hopf algebras with antipodesSHandSH′,respectively. Ifφ:H →H′is an?bialgebra morphism,thenφis an?Hopf algebra morphism,that is,SH′?φ=φ ?SH. Now we arrive at our main result of this subsection. Theorem 4.2Letkbe a field with char(k) = 0. LetXbe a set andjX:F(X,Ω),?xbe the natural embedding. Then the quintuple (HRT(X,Ω), mRT,1,Δ?, {|ω ∈Ω}) is the free Ω cocycle?unitary Hopf algebra onX. ProofThe quadruple (HRT(X,Ω), mRT,1,Δ?) is an?unitary Hopf algebra by Theorem 3.1.Together with the grafting operations{|ω ∈Ω},it is an Ω cocycle?unitary Hopf algebra by Eq.(3.6). LetHbe an Ω cocycle?unitary Hopf algebra. By Theorem 4.1, there is a unique morphism ˉf:HRT(X,Ω)→Hof Ω operated?unitary bialgebras,which is in particular a morphism of?bialgebras.So by Lemma 4.1, ˉfis compatible with the antipodes. Thus ˉfis an Ω operated?unitary Hopf algebra morphism. This proves the desired universal property. IfX=?,we obtain an freeness ofHRT(?,Ω),which is the Foissy Holtkamp Hopf algebra[14,22]. Corollary 4.1The quintuple (HRT(?,Ω), mRT,1,Δ?, {|ω ∈Ω}) is the free Ω cocycle?unitary Hopf algebra on the empty set, that is, the initial object in the category of Ω cocycle?unitary Hopf algebras. ProofIt follows from Theorem 4.2 by takingX=?. Further taking Ω to be singleton in corollaryllary 4.1,all decorated planar rooted forests have the same decoration. Equivalently,they are undecorated planar rooted forests studied in the Foissy Holtkamp Hopf algebra[14,22]. Corollary 4.2Let F be the set of planar rooted forests without decorations. Then the quintuple(kF, mRT,1,Δ?, B+) is the free cocycle?unitary Hopf algebra on the empty set, that is, the initial object in the category of cocycle?unitary Hopf algebras. ProofIt follows from corollaryllary 4.1 by taking Ω to be a singleton set.

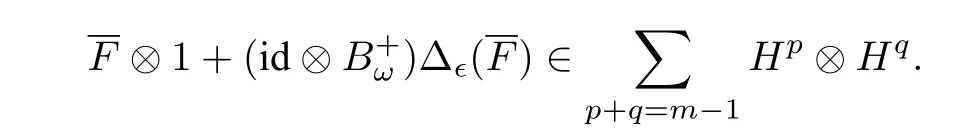
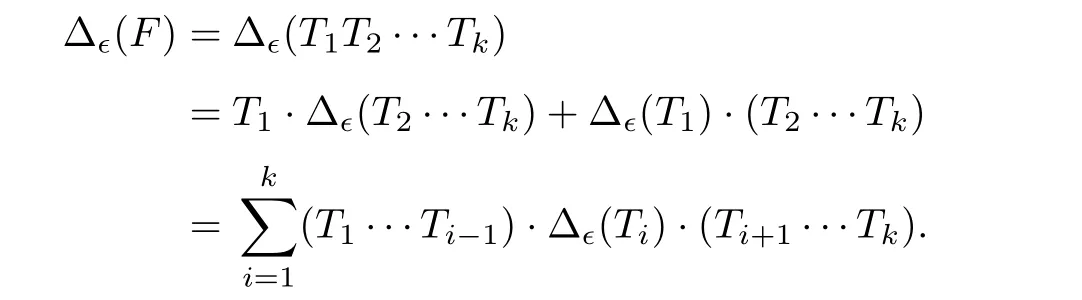
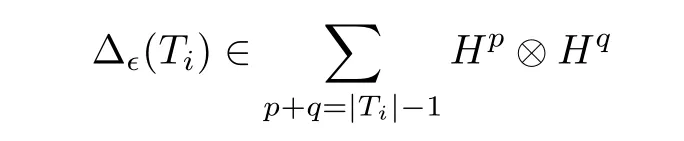
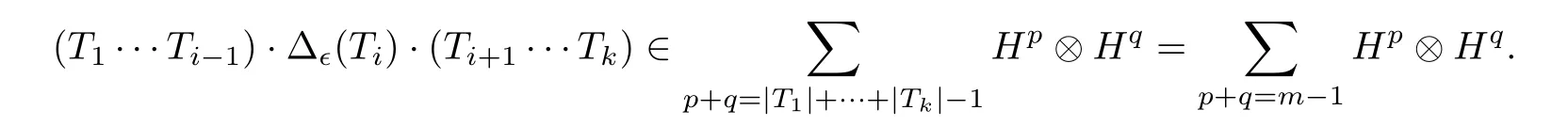
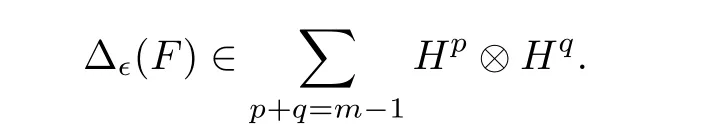
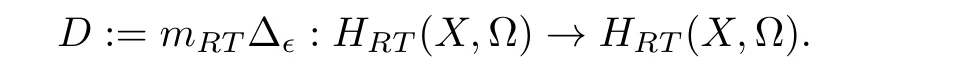
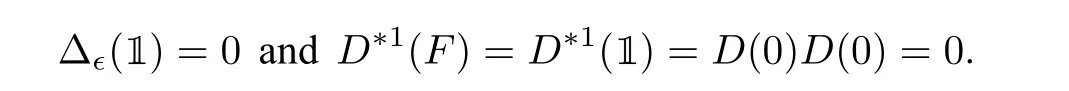
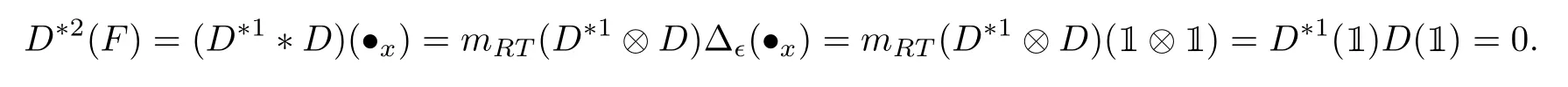
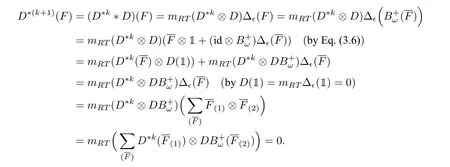
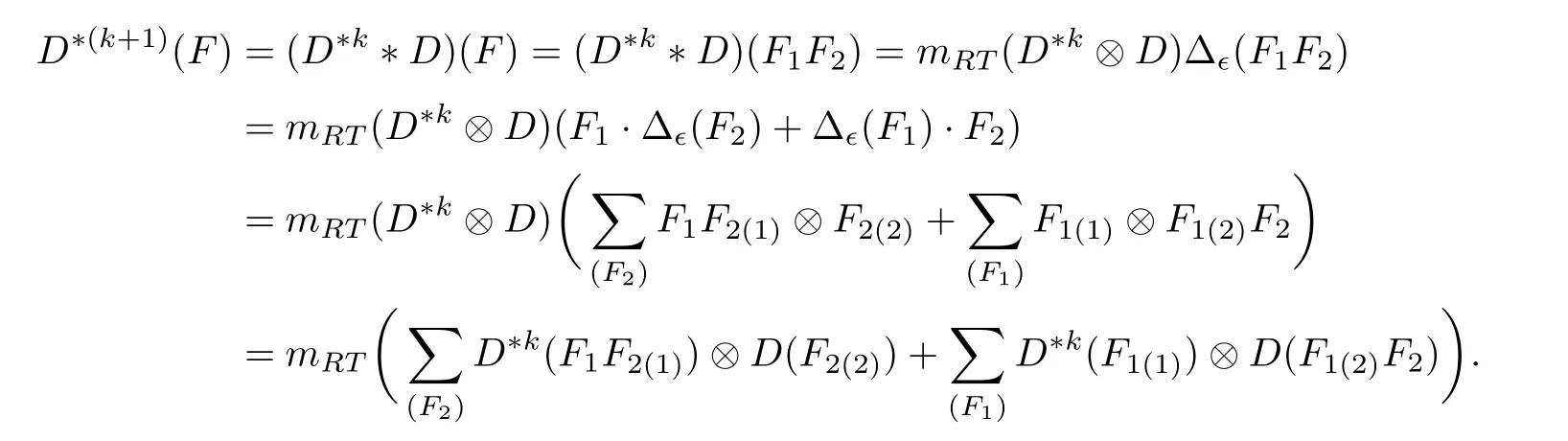
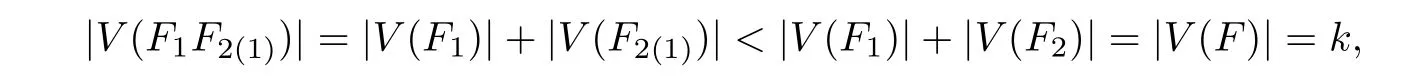
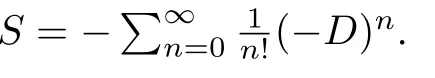
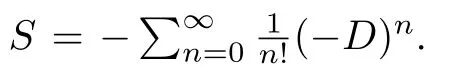
4 Free cocycle infinitesimal unitary Hopf algebras
4.1 Free cocycle infinitesimal unitary bialgebras
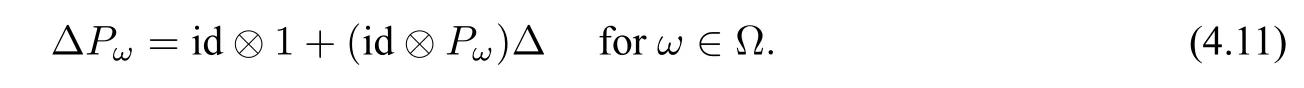
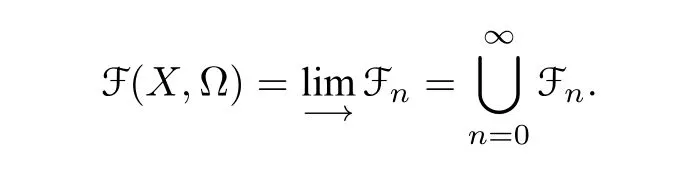
4.2 Free cocycle infinitesimal unitary Hopf algebras on rooted forests

