Nonlinear photoncurrent in transition metal dichalcogenide with warping term under illuminating of light?
Guo-Bao Zhu(朱國寶), Hui-Min Yang(楊慧敏), and Yun-Hai Zhang(張運(yùn)海)
School of Physics and Electronic Engineering,Heze University,Heze 274015,China
Keywords: photoconductivity,transition metal dichalcogenide,warping term
1. Introduction
With the rapid progress in synthesizing and characterizing, monolayer transition metal dichalcogenide (TMDC) has become a powerful candidate for its practical applications in future nanophotonic devices and technology. Monolayer TMDC is a direct band gap semiconductor. The inversion asymmetric crystal structure leads to spin valley coupling and valley contrasting Berry curvature.[1-4]Therefore,monolayer TMDC is a suitable candidate for optical manipulations, and provides access to many optoelectronic applications. It has been predicted that both valley Hall and spin Hall conductivities can be achieved in monolayer TMDC by circularly and linearly polarized light.[5-8]When the spin orbit coupling and warping term are absent,optical absorption in monolayer TMDC has been studied.[9,10]Furthermore,the ultrafast valley relaxation dynamics in monolayer MoS2was probed by nonequilibrium optical technique.[11]The effect of intense femtosecond laser excitation on the monolayer MoS2has been studied.[12]Moreover, femtosecond valley polarization and topological resonances in TMDC were studied by a single cycle of a strong circularly polarized optical field with duration of a few femtoseconds.[13]Photocurrent in TMDC also has been investigated.[14,15]However, the nonlinear response on external field in TMDC has been poorly understood.
We focus on the second-order nonlinear response,which has received increasing attention as a way to probe the topological properties of materials. There are a variety of secondorder nonlinear response including inject current,shift current,nonlinear Hall effect, and harmonic generation. The injection and shift mechanisms are two important ones of term.They are resulted from the transition of electron velocity and the transition of electron position during the optical excitation, respectively. They are second-order nonlinear optical effect, which has been attracting increasing interest and intensively investigated theoretically and experimentally.[16-27]Due to time-reversal symmetry breaking in magnetic systems,linearly polarized light can generate injection currents. An unusual photogalvanic effect has been predicted on the topological insulator surface when its semimetallic electronic spectrum is modified by an adjacent ferromagnet.[28]Ogawa et al.[29]demonstrated the generation of large zero-bias photocurrent in magnetic topological insulator thin films on mid-infrared photoexcitation.The combination of inversion symmetry breaking and finite tilts of the Weyl spectra can lead to significant photocurrents in three-dimensional Weyl semimetals.[30]The shift current is a steady-state photocurrent generated in the materials without inversion symmetry,originating from the geometric Berry phase of the constituting electron bands. The shift current has been proved to lead the ground breaking discoveries in Weyl semimetals,[31]tungsten disulfide nanotubes,[32]and silicon.[33]In experiment, the inject current can be detected by illuminating optical field,[34-36]and the shift current can be detected by short-circuit current measurements.[37,38]They have potential applications in energy harvesting,photon detection, nonlinear electronics, and quantum-confined spintronic devices.
Given these backgrounds, we present detail of studying on the photoncurrent in TMDC induced by a nonlinear optical interaction due to the illuminating of light. We focus on the injection and shift mechanisms. In TMDC,the warping term induces important modification on geometric tensor,which depends on valley and spin index. Furthermore, the photoncurrent in TMDC is governed by warping term and geometric tensor.
This paper is organized as follows. We firstly describe the model with warping term, and analyze band structure in Section 2,and present the results for Berry curvature and geometric tensor in Section 3. In Section 4,we present the results of the injection current and shift current.We analyze the effect of warping on geometric tensor,the valley photoconductivities of injection current, and the photoconductivities of shift current. Finally,we give a brief conclusion in Section 5.
2. Model
The effective two-band model of monolayer TMDC with warping term around the K and K′valleys(labeled by η=±1 respectively)is[1-4]
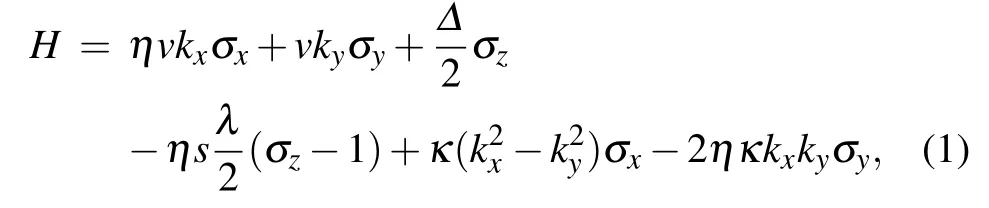
where v is the Fermi velocity,kx,yare components of the momentum measured relative to the K/K′point, σx,y,zare the Pauli matrices associated with the sublattice pseudospin,Δ is responsible for opening the band gap, 2λ is the spin splitting at the valence band top caused by the spin orbit coupling,and s is the index for spin. Here κ is responsible for the warping term,which is resulted from the lattice structure in TMDC.[1,2]Moreover,the warping term in honeycomb lattice can be tuned by Rashba spin-orbit coupling[39,40]or strain.[41]All energies are measured in units of v in this work.
For a two-band system, the Hamiltonian can always be expressed in terms of the Pauli matrices as

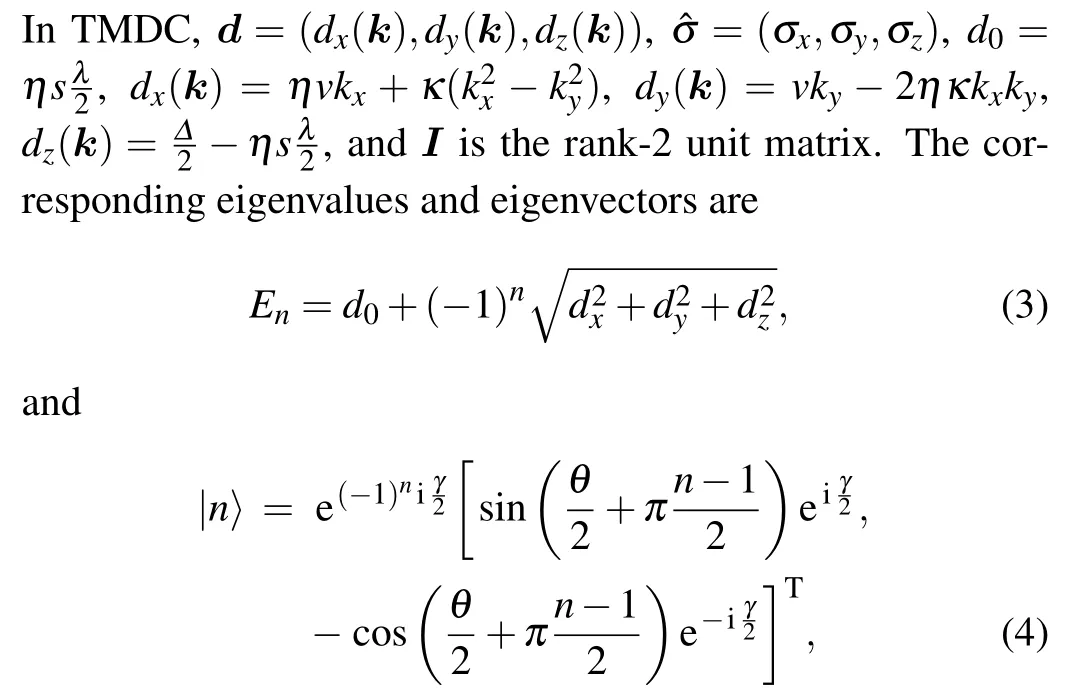
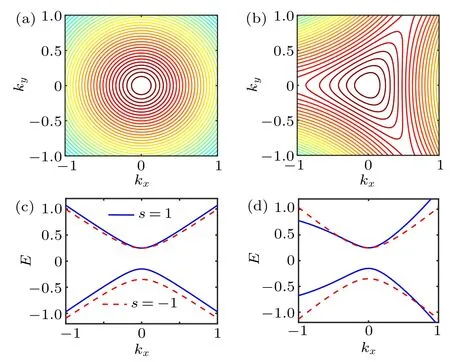
Fig.1. Contours plot of the corresponding valence band for monolayer TMDC in units of v without(a)and with(b)the warping term for η=1 and s=1 at fixed Δ =0.5v and λ =0.1v. The energy bands along ky =0 without(c)and with(d)the warping term. The blue solid lines denote spin-up bands and the red dashed lines correspond to spin-down bands.
3. Berry curvature and geometric tensor
In this section,we present the calculated results for Berry curvature and geometric tensor based on the following equations. Due to the good quantum numbers of spin and valley index,the corresponding Berry curvature in momentum-space for spin s and valley η component of the system is calculated by[42]
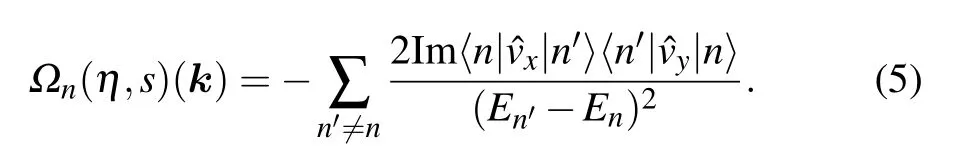
The summation is taken over all the occupied bands blow the bulk gap, and ?vx(y)is the velocity operator along x(y) direction. For our system, straightforward calculations show that the valley-and spin-dependent Berry curvature is

In Fig.2, we plot the Berry curvatures of valence band in 2D plane for spin-up electron state in monolayer TMDC around the two valleys in the absence/presence of the warping term. The corresponding Berry curvatures for spin-down electron states can be obtained by time reversal symmetry. Berry curvature has opposite signs in opposite valleys for the spin-up energy band. The Berry curvatures decay rapidly,and eventually vanish away from the valleys. In the absence of the warping term, Figs. 2(a) and 2(c) show that the Berry curvatures only depend on the module of k, which can be confirmed by Eq.(6). The Berry curvatures are prominently warped in the presence of the warping term. Therefore, the warping term leads to significant corrections to the magnitude of the Berry curvatures, which is dependent on spin (s) and valley index(η). The spin and valley resolved intrinsic Hall conductance can be calculated from the Berry curvature directly.Therefore,the spin and valley Hall conductance can be tuned by controlling the warping term.[43]On the other hand, the symmetry of our system and Berry curvatures are C3vwhen the trigonal warping term is included. Thus, the nonlinear Hall effect in warped TMDC is absent.[44]
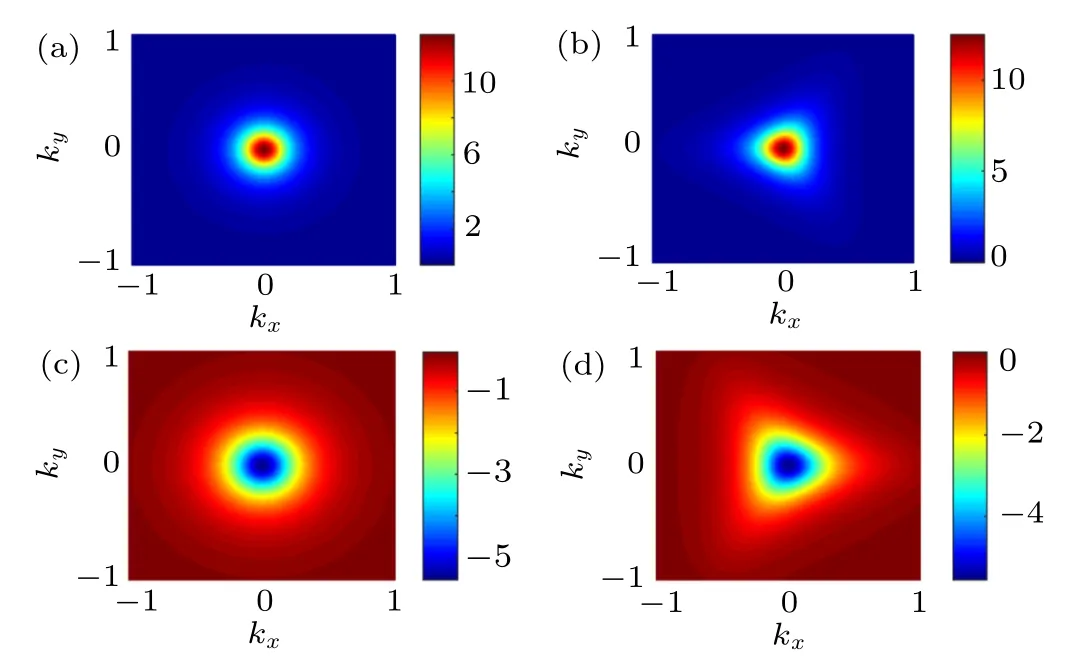
Fig.2.Berry curvatures of valence band for monolayer TMDC for s=1 at fixed Δ =0.5v and λ =0.1v. Here(a)and(b)are Berry curvatures without and with the warping term(κ =0.4)for valley η =1; (c)and(d) are Berry curvatures without and with the warping term (κ =0.4)for valley η =?1.
Next, we study the warping effect on the geometric tensor. The geometric tensor is defined as[45]
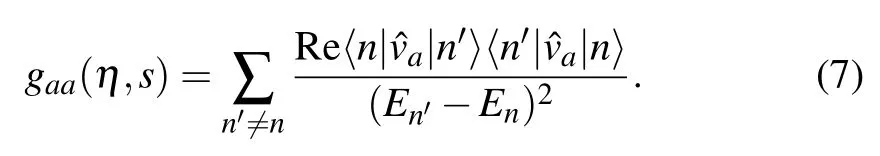
Based on the eigenvectors(Eq.(4))of our system,the valleyand spin-dependent geometric tensor in the valence band is obtained as follows:
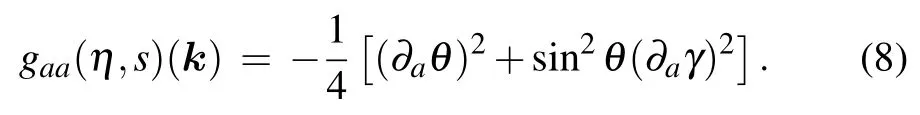
The geometric tensor distribution without(a)/(c)and with(b)/(d) the warping term are show in Fig.3 for s=1 at fixed Δ =0.5v and λ =0.1v, respectively. In contrast to that of Berry curvatures,the geometric tensors have the same signs at opposite valleys for the spin-up energy band. When the warping term is absent, we observe that the geometric tensors are peaked at the coordinate origin. Due to the warping term,the peaks will shift and split. Furthermore, the amplitudes of the peaks without and with the warping term are related to the valley index, which can be confirmed by the definitions of θ and γ. The amplitudes of the geometric tensor with or without the warping term in opposite valleys are different. Therefore,TMDC can be as a candidate for pseudospintronic(valley)devices, and the warping term will lead to the important modifications of physical quantity depending on geometric tensors.Moreover, the pseudospintronic (valley) transport should be studied due to the difference of the geometric tensor between the two valleys.
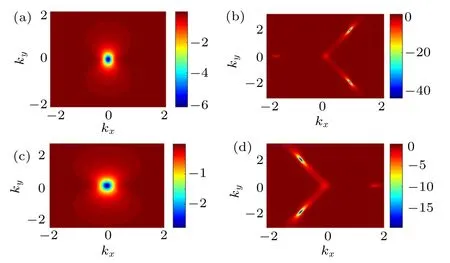
Fig.3. Geometric tensor gxx for monolayer TMDC without(a)/(c)and with(b)/(d)the warping term for s=1 at fixed Δ=0.5v and λ =0.1v.Here(a)and(b)are the geometric tensors without and with the warping term (κ =0.4) for valley η =1; (c) and (d) are the geometric tensors without and with the warping term(κ =0.4)for valley η =?1.
4. Injection current and shift current
In this section, we investigate the injection current and shift current, which are second-order optical effect with the induced direct current proportional to the square of electric field. For electric field at frequency ω,the photoconductivity of injection current and shift current are given by[16,26]



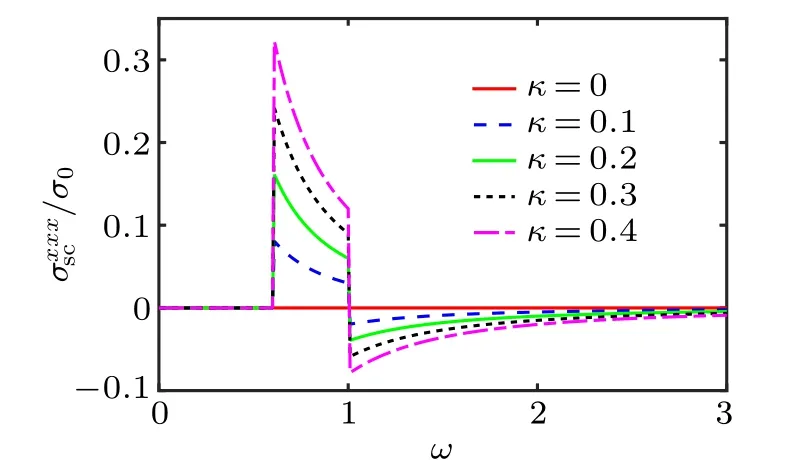
Fig.5.Photoconductivity of shift currentdependence on ω in units of σ0= at δ =0.1v and λ =0.4v for κ=0,0.1,0.2,0.3,and 0.4,respectively.
Based on the results of the photoconductivities of inject and shift current, we can find that the warping term is playing an essential role in the nonlinear transport properties of materials. In TMDC, the warping term is due to the intrinsic lattice structure, which is different from the other materials. In graphene, the system shows the warped band structure when the Rashba spin-orbit coupling is stronger than the intrinsic spin-orbit coupling.[39]Considering a uniform uniaxial strain, graphene will has anisotropic warping term.[41]When the strength of the Rashba SOC becomes comparable to the hopping energy, silicene shows a warped low-energy Hamiltonian.[40]
5. Conclusions
In conclusion, we have studied the photoconductivities of injection current and the shift current in transition metal dichalcogenide with the warping term in the presence of the sublattice potential and the spin orbit coupling. It is found that there are the valley photoconductivities of injection current and the photoconductivities of shift current in the system.Moreover, we find that the the photoconductivities are determined by warping term and geometric tensor, and controlled by the interplay between the sublattice potential and the spin orbit coupling. Our findings provide a way to control the nonlinear transport properties of materials,and a approach to detect the geometric tensor by nonlinear optical response.
——鐘表也要萌萌噠
- Chinese Physics B的其它文章
- Nonlocal advantage of quantum coherence in a dephasing channel with memory?
- New DDSCR structure with high holding voltage for robust ESD applications?
- Modeling and analysis of car-following behavior considering backward-looking effect?
- DFT study of solvation of Li+/Na+in fluoroethylene carbonate/vinylene carbonate/ethylene sulfite solvents for lithium/sodium-based battery?
- Multi-layer structures including zigzag sculptured thin films for corrosion protection of AISI 304 stainless steel?
- Preparation of AlN film grown on sputter-deposited and annealed AlN buffer layer via HVPE?

