Nonlocal advantage of quantum coherence in a dephasing channel with memory?
Ming-Liang Hu(胡明亮), Yu-Han Zhang(張宇晗), and Heng Fan(范桁)
1School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China
2Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
3CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China
4Songshan Lake Materials Laboratory,Dongguan 523808,China
Keywords: quantum coherence,correlated quantum channel,memory effects
1. Introduction
Quantum coherence is an embodiment of the superposition principle of states. It characterizes quantumness of a state that marks the departure of quantum theory from classical physics.[1]Recent studies further reveal that quantum coherence underpins different forms of quantum correlations[2]and is also responsible for the power of emerging quantum communication and computation tasks.[3]Hence, it is crucial to characterize it quantitatively. Baumgratz et al.[4]made a first step toward this problem. They introduced the defining conditions for a faithful coherence measure, together with two coherence measures defined by the l1norm and the relative entropy. Such a progress stimulates a number of subsequent studies focused on quantifying coherence, such as the entanglement-based coherence measures,[5]the robustness of coherence,[6,7]the skew information measure of coherence,[8,9]and those convex roof measures of coherence.[10-12]
Starting from these coherence measures, the roles of coherent states in the quantum information processing tasks such as quantum state merging,[13]deterministic quantum computation with one qubit,[14]quantum heat engine,[15]quantum metrology,[6,9,16]and several quantum algorithms,[17,18]have been explored. Moreover, these coherence measures can also be used to interpret the wave-particle duality[19,20]and to detect quantum phase transitions in various spin-chain systems.[21-25]
The above coherence measures are also useful in interpreting quantum correlations.[2]Besides the entanglementbased coherence measures,[5]the progresses in this respect include the interpretations of quantum entanglement[12,26]and various discord-like quantum correlations[26-29]by considering distribution of quantum coherence among the subsystems.Another route for connecting quantum coherence to quantum correlations can be achieved by considering the steered coherence of a state.[30-33]In particular, by virtue of the mutually unbiased bases, Mondal et al.[31]introduced the nonlocal advantage of quantum coherence (NAQC) for a twoqubit state,which was subsequently generalized to the(d×d)-dimensional states(d is a prime power),[32]and it is shown that it characterizes a type of quantum correlation stronger than entanglement. For the two-qubit states,the connection between NAQC and Bell nonlocality was also established.[33]
Due to its practical role in quantum information processing, it is significant to seek ways to protect the NAQC in the noisy environments. For the case of the surrounding noise acting independently on each qubit of a system, the freezing of coherence[34-37]and the decay of coherence[38-40]have already been studied. But if the time windows for a sequence of qubits being inside a channel are partially overlapped, the actions of this channel may be correlated. In fact, for the correlated Pauli channel introduced phenomenologically,[41-43]its influence on entropic uncertainty,[44]quantum coherence,[45,46]and quantum Fisher information[47]have been explored. In this paper,we consider a Hamiltonian model of correlated dephasing channel.[48-50]We will show that the memory effects arising from correlated actions of such a Hamiltonian dephasing channel on NAQC are state dependent, and the decay rate of NAQC for the input Bell-like states with only one excitation can be suppressed evidently.


while for two qubits traversing the channel subsequently,one has γ03,30=γ+and γ12,21=γ?,with
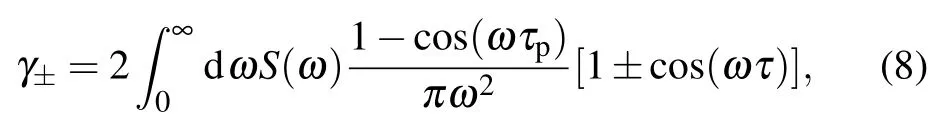
and the remaining γjlwith j/=l equal γ0. For N ≥3,one can also obtain γjlfrom Eq. (6),but as we consider the NAQC of two qubits,we do not list them here.
The decoherence rates γ0and γ±are different for the channels with different spectral densities. In the following,we consider the Lorentzian spectrum
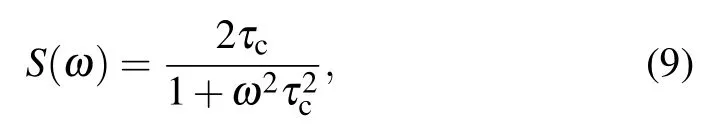
for which γ0and γ±can be derived analytically as
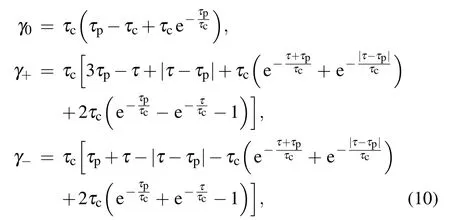
with τcbeing the correlation time scale of the channel.
From Eqs.(7)and(8),one can note that the memory effect of the channel originates from γ±/=2γ0,that is,the actions of the channel on two consecutive qubits cannot be factorized as those on each one. Then, it is natural to introduce the following factor:[49]
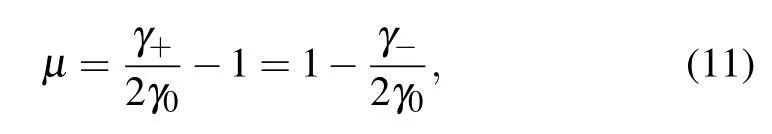
to characterize such a memory effect,where the second equality is due to γ++γ?=4γ0,see Eqs.(7)and(8). Moreover,we would like to remark here that the origin of this memory effect is different from that of the non-Markovian memory effect due to the temporal correlations in the evolution process of each qubit. It characterizes the memory related to the history of the multiple uses of a channel,whereas the non-Markovian memory effect characterizes the back-flow of information from the environment to the central system.[41]
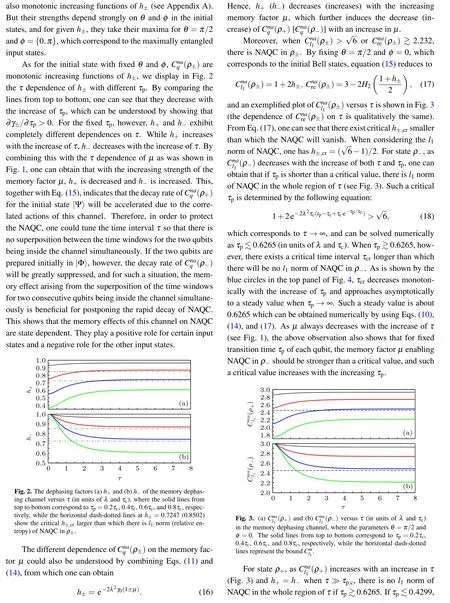
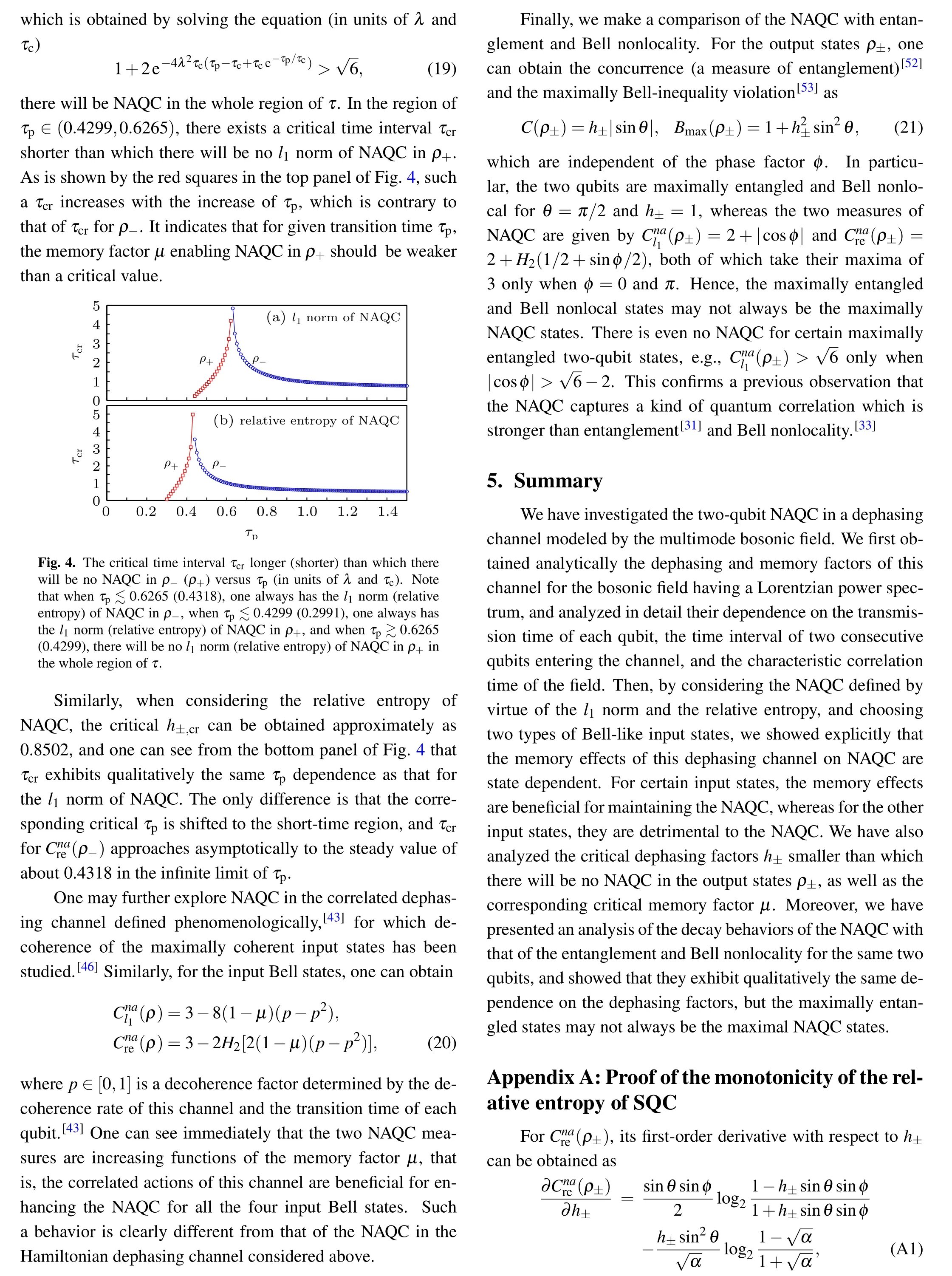
From Eqs. (10) and (11), one can see that the memory factor μ is determined by τ/τcand τp/τc, so we display in Fig.1 the τ dependence ofμ with different τp(in units of τc).From this figure,one can see that for the given transition time τpof each qubit,μ decreases with the increasing time interval τ that separates two consecutive qubits entering the dephasing channel. Such an observation is understandable because with the increase of τ,the channel is reset to its initial state gradually,and in the limit of τ ?τp,c,one has γ±=2γ0andμ =0.Thus its actions on the two qubits are uncorrelated.In the limit of τ,τp?τc, however, one has γ+=4γ0and γ?=0, which corresponds toμ =1. So the consecutive actions of the channel are fully correlated. For the general case ofμ ∈(0,1),the channel has partial memory about its actions on two consecutive qubits passing through it.

Fig.1. The memory factor μ of the memory dephasing channel versus τ (in units of τc),where the lines from bottom to top correspond to τp=0.5τc,τc,1.5τc,and 2τc,respectively.
4. NAQC in the memory dephasing channel
Based on the above preliminaries, we explore effects of the Hamiltonian dephasing channel on NAQC in this section.We consider the case of two qubits being prepared initially in one of the following Bell-like states:
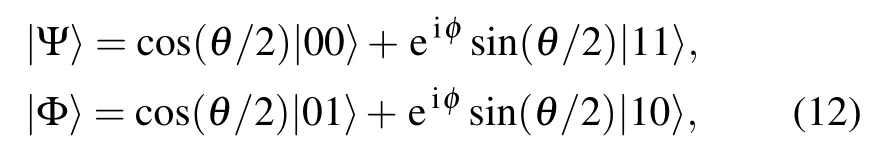
where θ ∈[0,π]and φ ∈[0,2π]. By using Eq.(5),the corresponding output state ρ+for the initial state |Ψ〉 and ρ?for the initial state|Φ〉can be obtained as

where the dephasing factors h±are given by

Then by the definition of NAQC in Eq.(2),one can obtain
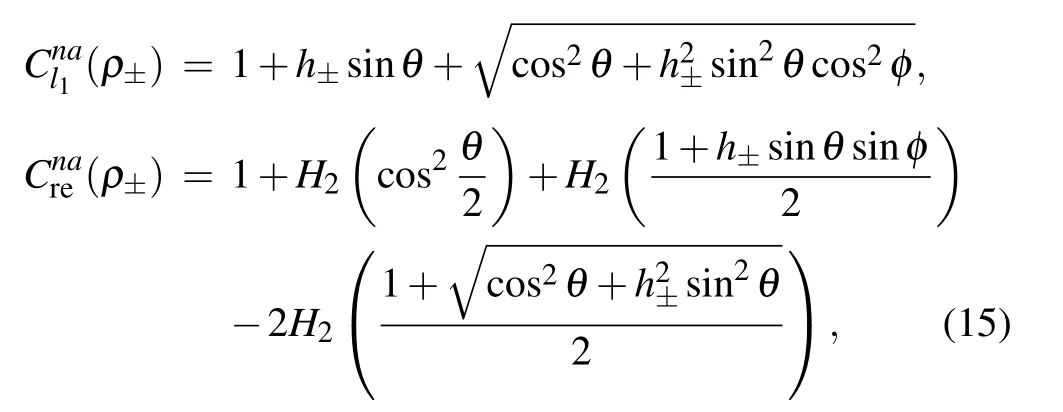


- Chinese Physics B的其它文章
- New DDSCR structure with high holding voltage for robust ESD applications?
- Nonlinear photoncurrent in transition metal dichalcogenide with warping term under illuminating of light?
- Modeling and analysis of car-following behavior considering backward-looking effect?
- DFT study of solvation of Li+/Na+in fluoroethylene carbonate/vinylene carbonate/ethylene sulfite solvents for lithium/sodium-based battery?
- Multi-layer structures including zigzag sculptured thin films for corrosion protection of AISI 304 stainless steel?
- Preparation of AlN film grown on sputter-deposited and annealed AlN buffer layer via HVPE?

