劉紅炎

(武漢大學數(shù)學與統(tǒng)計學院,湖北武漢430072)

1 引言

邊界唯一性定理是將Schwarz引理應用到邊界上時產生的.1994年,Burns-Krantz[1]研究邊界上的Schwarz引理,得到了全純映射的一些剛性結果,也就是邊界唯一性的結果,主要分別得到了在單位圓盤,單位球和強擬凸域上的一些結論.在單位球上的結論如下.

定理1.1[1](Burns-Krantz)設f:Bn→Bn是單位球到自身的全純映射,滿足當z→1時(這里1=(1,0,···,0))f(z)=z+O(|z-1|4),則f(z)≡z于單位球內.

自從Burns-Krantz的工作之后,邊界Schwarz引理開始被越來越多的學者研究.例如2015年Liu-Wang-Tang做出了單位球中的一類邊界Schwarz引理[2],2018年Tu-Zhang得到了對稱雙圓盤上的邊界Schwarz引理[3].在1995年X.Huang將其做到有界弱擬凸域上和強凸域上[4],其在強凸域中設定一個不動點,然后把上述定理中的4次降到了3次.其在單位球上的相關結論如下.

定理1.2[4](Xiaojun Huang)設f:Bn→Bn是單位球到自身的全純映射,滿足當z→1時f(z)=z+O(|z-1|3)且f(z0)=z0,其中z0∈Bn,則f(z)≡z.

以上兩個定理是在單位球上的經典結果,接下來看一下在Fock-Bargmann-Hartogs域上已有的結果.首先引入這類區(qū)域的定義,Fock-Bargmann-Hartogs域Dn,m定義如下

Fock-Bargmann-Hartogs域是一類無界強擬凸域,2013年Yamamori給出了這類域的Bergman核函數(shù)[5];2016年Bi-Feng-Tu給出了這個域上的平衡度量[6].可以從上述兩個文獻中更好地了解Fock-Bargmann-Hartogs域.

2006年,Baracco-Zaitsev-Zampieri將之前Burns-Krantz的邊界唯一性結果推廣到了強擬凸流形上[7],我們提取其在Fock-Bargmann-Hartogs域上的結論如下.

定理1.3[7](Baracco-Zaitsev-Zampieri)設f:Dn,m→Dn,m是從Fock-Bargmann-Hartogs域到自身的全純映射,滿足當(z,w)非切向逼近(1,0)時(這里0=(0,···,0))

則F(z,w)≡(z,w).

2018年,Liu-Chen-Pan得到了一種單位球上不等維的邊界唯一性定理[8],他們將f第一個分量函數(shù)設定為僅關于z第一個分量的恒等函數(shù),并在邊界點1增加了C2的條件之后也得到了可以把指數(shù)估計降低一階的結果,而且直接做出不等維情形的結果.如下定理是他們的主要結論.

定理1.4[8](Liu-Chen-Pan)設f:Bn→BN,N≥n≥1是從單位球Bn到BN的全純映射,滿足當z→1時

若f在點1處是C2的,并且f1(z)=z1,這里f1是f的第一個分量函數(shù),z1是z的第一個坐標分量,則f(z)≡(z,0).

受到他們的啟發(fā),本文得到了一些不等維的邊界唯一性定理的結果,也就是對Burns-Krantz型定理從等維情形推廣到不等維情形.

2 主要定理

這一節(jié)介紹本文的主要結果及其證明,本節(jié)前三個定理是對上一節(jié)中敘述到的邊界唯一性定理的推廣,后兩個定理是受前述結果啟發(fā)做出的邊界唯一性定理的結果.首先將Burns-Krantz單位球上的定理1.1推廣為不等維單位球之間的定理.

定理2.1設f:Bn→Bm,n≤m是一個全純映射,滿足當z→1時有

則f(z)≡(z,0).

證n≤m,f=(f1,f2,···,fm),令g=(f1,···,fn). 由于

則g是一個從單位球Bn到自身的全純映照.注意到定理中的條件f(z)=(z,0)+O(|z-1|4),(z→1)再結合如下不等式|g(z)-z|≤|f(z)-(z,0)|,得到

此時g(z)滿足定理1.1中的條件,則g(z)≡z.

設f=(g,h),當z→?Bn,z∈Bn時,有|g|→1,而|g|2+|h|2=1,則|h|→0.由全純函數(shù)的最大模原理可以得到:h=0.故f(z)≡(z,0).定理2.1證畢.

注2.1以上定理中有n≤m的條件,是由于當n＞m時,并不能有類似推廣.也就是說如果f:Bn→Bm,n＞m是全純映照,滿足當z→1時有

此時不能得到f(z)≡(z1,z2,···,zm).

則f是從Bn到Bm的全純映照,并且滿足式(2.1)的條件,但f(z)/=(z1,z2,···,zm).注2.1完畢.

然后注意到類似上述定理2.1的方法還可以用來將1995年Huang的結果(定理1.2)推廣到不等維的單位球之間,如下定理結論.

定理2.2設f:Bn→Bm,n≤m是一個全純映射,滿足當z→1時有

且存在z0∈Bn使f(z0)=(z0,0),則f(z)≡(z,0).

證n≤m,f=(f1,f2,···,fm). 令g=(f1,f2,···,fn),由于

則g是一個從單位球Bn到自身的全純映照.注意到定理中的條件f(z)=(z,0)+O(|z-1|3),(z→1)再結合如下不等式|g(z)-z|≤|f(z)-(z,0)|,得到

由于f(z0)=(z0,0),故g(z0)=z0.于是g(z)滿足定理1.2中的條件,則g(z)≡z.

令f=(g,h),當z→?Bn,z∈Bn時,有|g|→1,又|g|2+|h|2=1,則|h|→0.由全純函數(shù)的最大模原理可以得到:h=0.故f(z)≡(z,0).定理2.2證畢.

對于定理2.2也有類似定理2.1的注記,即在n＞m時沒有類似推廣,可以列舉出相應反例.

以上兩個定理就是本文在單位球上的主要結論.接下來將著眼于本文探討的第二類區(qū)域,Fock-Bargmann-Hartogs域,下述定理是本文在此區(qū)域上的第一個主要定理,是將2006年Baracco-Zaitsev-Zampieri的定理1.3推廣到不等維.

定理2.3設F:Dn,m→DN,M,n≤N,m≤M是一個全純映射,滿足當(z,w)非切向逼近(1,0)時有

則F(z,w)≡(z,0,w,0).

證F=(f,g)=(f1,f2,···,fN,g1,g2,···,gM). 令G=(f1,···,fn,g1,···,gm),注意到如下不等式

則G是一個從Fock-Bargmann-Hartogs域Dn,m到自身的一個全純映照.注意到定理中的條件當(z,w)非切向逼近(1,0)時

再結合如下不等式

得到當(z,w)非切向逼近(1,0)時

此時G(z,w)滿足定理1.3中的條件,則G(z,w)≡(z,w),即

注意如下不等式

當(z,w)→?Dn,m,(z,w)∈Dn,m時,有|z|2→e-μ|w|2.則由上述不等式可知

由全純函數(shù)的最大模原理可以得到fn+1=···=fN=gm+1=···=gN=0,(z,w)∈Dn,m.故F(z,w)≡(z,0,w,0).定理2.3證畢.

受Liu-Chen-Pan固定一個分量函數(shù)為對應坐標恒等函數(shù)的啟發(fā),本文得到一個Fock-Bargmann-Hartogs域上的固定坐標分量函數(shù)的不等維邊界唯一性定理結論,這里的估計次數(shù)是3次,對坐標分量及邊界點處的條件要求比較高,定理結論及證明如下.

定理2.4設F:Dn,m→DN,M,n≤N,m≤M是一個全純映照,是Dn,m的邊界點.當時,有

設F=(f,g)=(f1,···,fN,g1,···,gM),F在點處是C2的,f1(z,w)=z1,gi(z,w)=wi,1≤i≤m,則F(z,w)≡(z,0,w,0).

證固定w0,將F(z,w0)看做關于z的全純映射.當時有

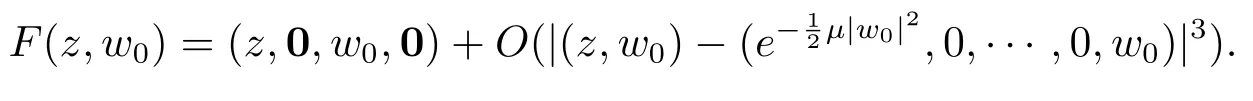
注意到

對f(z,w0)的范圍作如下估計

則f(z,w0)是如下關于z的全純映照

由題設條件知,f(z,w0)在點處是C2的.接下來考慮則其是定義在單位球Bn上的全純映射,且有當時,成立

這也就是當z→(1,0,···,0)時成立

構造函數(shù)

則h:Bn→BN是從單位球Bn到BN的全純映照,h在點(1,0,···,0)處是C2的.由于f1(z,w0)=z1,由h的表示式可以看出h1(z)=z1.并且由(2.2)式知當z→(1,0,···,0)時有

則由定理1.4得h(z)≡(z,0),z∈Bn.進而得到f(z,w0)=(z,0).由w0的任意性,f(z,w)=(z,0).故F(z,w)=(z,0,w,gm+1,···,gM).注意如下不等式

此時令(z,w)→?Dn,m,(z,w)∈Dn,m,則|z|2→e-μ|w|2.則由上述不等式知|gm+1|2+···+|gM|2→0,因此由全純函數(shù)的最大模原理得gm+1=···=gM=0.故F(z,w)≡(z,0,w,0).定理2.4證畢.

然后繼續(xù)順著上述定理2.4的思路,得到一個類似Burns-Krantz定理(定理1.1)推論的一個在Fock-Bargmann-Hartogs域上的結果,其與定理2.4條件相比較減少了一個邊界點處正則性的條件,少固定了一個分量,但其估計次數(shù)是4次.此定理結果表述如下.

定理2.5設F:Dn,m→DN,M,n≤N,m≤M是一個全純映照,是Dn,m的邊界點.當時,有

設F=(f,g)=(f1,···,fN,g1,···,gM),其中gi(z,w)=wi,1≤i≤m,則F(z,w)≡(z,0,w,0).

證用類似定理2.4中證明的方法,將w0固定,則可以把F(z,w0)看作是關于z的全純映射.由于當時有

注意到

對f(z,w0)的范圍作如下估計

則f(z,w0)是如下關于z的全純映照

這也就是當z→(1,0,···,0)時成立

構造函數(shù)

則h:Bn→BN是從單位球Bn到BN的全純映照,由(2.3)式知當z→(1,0,···,0)時有

則由定理2.1得h(z)≡(z,0),z∈Bn.進而得到f(z,w0)=(z,0).由w0的任意性,f(z,w)=(z,0).故F(z,w)=(z,0,w,gm+1,···,gM).注意如下不等式

再令(z,w)→?Dn,m,(z,w)∈Dn,m,則|z|2→e-μ|w|2.則由上述不等式知|gm+1|2+···+|gM|2→0.由最大模原理得gm+1=···=gM=0.故F(z,w)≡(z,0,w,0).定理2.5證畢.