概率2-度量空間中Φ-壓縮映象對的公共不動點
張樹義, 聶 輝
(渤海大學 數理學院, 遼寧 錦州 121013)
關于概率度量空間和模糊度量空間概念及在此空間中建立的不動點定理,文獻[1-12]做過研究,其中文獻[3]使用控制函數在G-完備Menger概率度量空間研究了一類映象的不動點的存在性.文獻[4-6]在非阿基米德概率2-度量空間中建立了幾類映象不動點定理,文獻[7]在非阿基米德概率度量空間中建立了Altman型映象的公共不動點定理,文獻[8-9]在模糊度量空間中利用模糊度量M滿足三角不等式的概念建立了一類壓縮映象公共不動點定理.文獻[10-12]在模糊度量空間中利用模糊度量M滿足三角不等式的概念建立了一類積分型以及Φ-壓縮型映象的不動點定理推廣了文獻[8-9]中的結果.近年來,文獻[13-15]研究了幾類非線性映象不動點的存在性與迭代逼近.受上述工作啟發(fā),本文在一定條件下,在Menger概率2-度量空間中建立一類Φ-壓縮映象對新的公共不動點的存在性定理.
1 預備知識
下面回憶一些基本概念, 其中定義1~4可在文獻[1-7]查到.
定義1 映象f:=(-∞,+∞)→+=[0,+∞)稱為分布函數,如果它是不減的,左連續(xù)的,
定義2 映象Δ:[0,1]×[0,1]×[0,1]→[0,1]稱為三角范數(簡稱t-范數),如果滿足以下條件
ⅰ) ?a∈[0,1],Δ(a,a,1)=a;
ⅱ) ?a,b,c∈[0,1],Δ(a,b,c)=
Δ(a,c,b)=Δ(c,a,b);
ⅲ) ?a,b,c,d,e,f∈[0,1],若a≥d,b≥e,
c≥f,有Δ(a,b,c)≥Δ(d,e,f);
ⅳ) ?a,b,c,d,e∈[0,1],Δ(Δ(a,b,c),d,e)=Δ(a,Δ(b,c,d),e)=Δ(a,b,Δ(c,d,e)).
定義3 (X,F,Δ) 稱為Menger概率2-度量空間,如果X是非空集,Δ是t-范數,D為全體分布函數,F:X×X×X→D,記分布函數F(x,y,z)為Fx,y,z,而Fx,y,z(t)表示Fx,y,z在t∈的值.若滿足下面條件:
ⅰ)Fx,y,z(0)=0,?x,y,z∈X;
ⅱ) 對?x,y∈X,存在z∈X,t0>0,使得
0≤Fx,y,z(t0)<1;
ⅲ)Fx,y,z(t)=1,?t>0,則x,y,z至少有2個相等;
ⅳ)Fx,y,z=Fx,z,y=Fy,z,x,?x,y,z∈X;
ⅴ) 若?x,y,z,w∈X,?t1,t2,t3∈
[0,+∞),有
定義4 設(X,F,Δ)是Menger概率2-度量空間,序列{xn}?X. 如果對?ε>0,λ>0,a∈X,存在N(ε,λ,a)∈(正整數集),使得?n≥N,有Fxn,x,a(ε)>1-λ,則稱{xn}收斂到點x∈X.如果對?ε>0,λ>0,a∈X,存在N(ε,λ,a)∈,使得對?n,m≥N,有Fxn,xm,a(ε)>1-λ,則稱{xn}為Cauchy序列.如果X中的每個Cauchy序列都收斂,則稱(X,F,Δ)是完備的.
定義5 Menger概率2-度量空間(X,F,Δ)中的序列{xn}稱為G- Cauchy序列,如果對每一個p∈,如果X中的每個G- Cauchy序列都是收斂的,則稱為Menger概率2-度量空間(X,F,Δ)是G- 完備的.
設Ω={g|g:[0,1]→[0,∞)連續(xù),嚴格遞減,g(1)=0,g(0)=+∞}.
定義6[6]Menger概率2-度量空間(X,F,Δ)稱為(C)g型的,如果存在g∈Ω,使得?x,y,z,w∈X,?t≥0,有gFx,y,z(t)≤gFx,y,w(t)+gFx,w,z(t)+gFw,y,z(t).
定義7 設(X,F,Δ)是概率2-度量空間,概率2-度量F稱為三角的,如果?x,y,z,w∈X, ?t>0,有
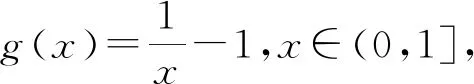
Φ1={Φ|Φ:[0,+∞)→[0,+∞),Φ(0)=0}.
由文獻[6]易知下面引理1成立.
引理1[6]設(X,F,Δ)是(C)g型的概率2-度量空間,{xn}?X,?t>0,如果?a∈X,有
則對?n,m≥1,有Fxn,xn+1,xm(t)=1,其中Φ∈Φ1,0 以下設t-范數Δ是連續(xù)的. 定理1 設(X,F,Δ)是(C)g型的G- 完備Menger概率2-度量空間,f與h是X上的自映象,滿足下列不等式組: 其中,φ:+=[0,+∞)→+是勒貝格可積與可和的,且φ(t)dt>0,ε>0.Φ∈Φ1,?x∈X,t>0,0 證明 對x0∈X, 可歸納定義序列{xn}為x2n+1=fx2n,x2n+2=hx2n+1,n=0,1,2…,如果對某個n,xn=xn+1, 則易知xn是f與h在X上一公共不動點.以下假設對任意n≥0,xn≠xn+1, 由式(2),對?t>0,?a∈X,有 類似,由式(1) ?t>0,?a∈X,可得 由式(3)和式(4),?t>0,?a∈X,有 于是n≥0,t>0,?a∈X,有 從而 連續(xù)n次使用上面不等式有 由式(5),?t>0,?a∈X, 有 于是對?t>0,?a∈X,有Fxn+1,xn+2,a(t)→1(n→∞).據定義3,?t>0,?a∈X,有 由引理1,并在式(6)中令n→∞,對任意p∈,?t>0,?a∈X,有Fxn,xn+p,a(ε)→1(n→∞).因此{xn}是一G- Cauchy序列. 由于(X,F,Δ)是G- 完備的,于是存在z∈X,使由f的連續(xù)性,因此z是f不動點.由式(2)?t>0,?a∈X,有 從而?t>0,?a∈X,有gFhz,z,a(t)=0,于是hz=z.故z是f與h在X上一公共不動點.類似,h連續(xù)性,f與h在X上有一公共不動點.證畢. 注2 定理1中附加 ⅰ) 取Φ(t)=λt(0<λ≤1),0 ⅱ)Φ(t)=λt(0<λ<1),0 在定理1令f=h,C=max{A,B},則有 推論1 設(X,F,Δ)是G- 完備Menger概率度量空間,f是X上的自映象滿足下列不等式 其中,φ:+=[0,+∞)→+是勒貝格可積且φ(t)dt>0,ε>0.?x∈X,t>0,0 如果f連續(xù),則f在X上有一不動點. 注3 在定理1中若用完備的Menger概率度量空間代替G- 完備的Menger概率度量空間,而連續(xù)t-范數取為Δ(α,β)=min{α,β},α,β∈[0,1],則容易證明定理1也成立. 由注1和定理1可得如下結果. 定理2 設(X,F,Δ)是具有F三角的G- 完備Menger概率2-度量空間,f與g是X上的自映象,滿足下列不等式組: 其中,φ:+=[0,+∞)→+是勒貝格可積與可和的,且φ(t)dt>0,ε>0.?x∈X,t>0,0 如果f或h連續(xù),則f與h在X上有一公共不動點. 隨著不動點理論的發(fā)展, 提出新的不動點存在性定理借以統(tǒng)一以往的研究成果, 是不動點理論發(fā)展趨勢之一. 本文在Menger概率2-度量空間框架下, 利用控制函數建立一類積分型Φ-壓縮映象對新的公共不動點的存在性定理, 最終將相關文獻中的結果推廣到了積分型Φ-壓縮映象對的情形, 擴展了其不動點定理的適用范圍.
2 主要結果
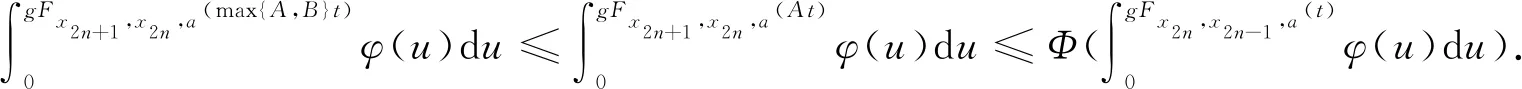
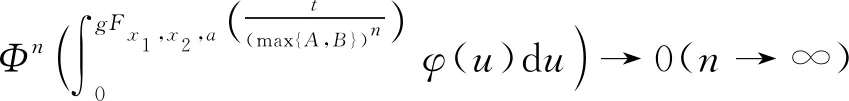
3 結 論

