◇ 山東 賈榮林

空間向量基本定理與平面向量基本定理相似,都是用相同的一組向量(基底)表示不同的向量.空間向量基本定理是溝通空間所有向量的一個橋梁,通過它可以消除不同空間向量之間的差異,實現(xiàn)某種求解目的.本文結(jié)合實例剖析空間向量基本定理的應(yīng)用.

1 向量分解問題

例1平行六面體ABCD-A1B1C1D1中,M為AC和BD的交點(diǎn),若則下列式子中與相等的是( ).

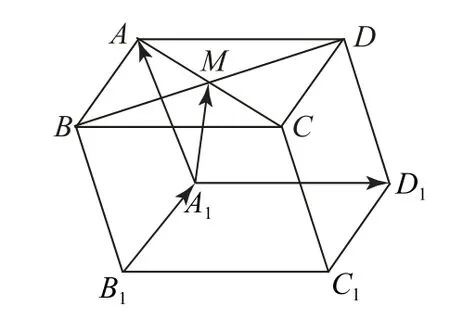
圖1

解析

點(diǎn)評

空間向量基本定理為空間向量的分解提供理論基礎(chǔ),空間中任意三個不共面向量都可以作為空間向量的一個基底,基底選定以后,空間的所有向量均可由基底唯一表示.

2 參數(shù)求解問題

例2已知正方體ABCD-A1B1C1D1中,點(diǎn)E為上底面A1C1的中心,若則x,y的值分別為( ).

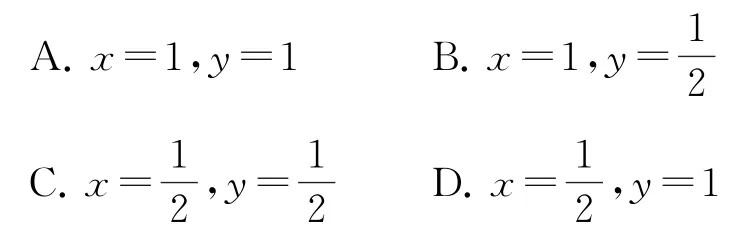
解析

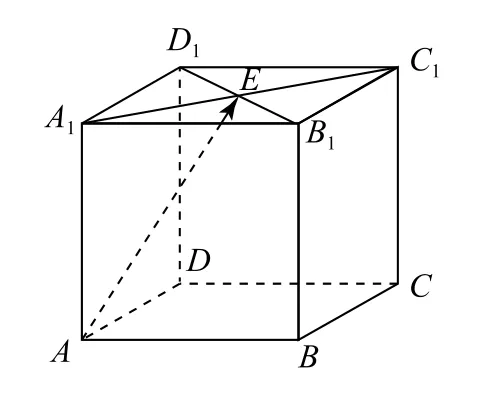
圖2

點(diǎn)評

空間向量基本定理恰好說明用空間三個不共面的向量組{a,b,c}可以表示出空間中任一向量,而且a,b,c的系數(shù)是唯一的,由此可以用來求解一些空間向量線性表達(dá)式或某些參數(shù)問題.

3 關(guān)系量求值問題

例3如圖3,正三棱柱ABC-A1B1C1的各棱長都為2,E,F分別是AB,A1C1的中點(diǎn),則EF的長是( ).

圖3

解析

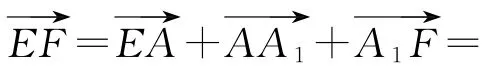
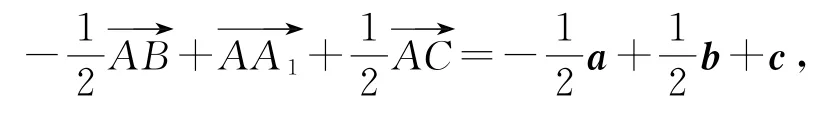
所以

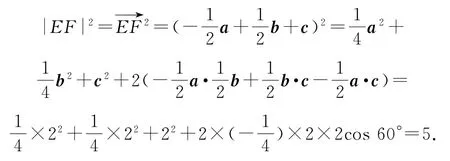
綜上,EF的長是,故選C.

點(diǎn)評

在解決空間向量中有關(guān)線段的長度、向量間的夾角以及位置關(guān)系等關(guān)系量的求值與應(yīng)用問題時,往往先設(shè)出基底向量{a,b,c},利用空間圖形的相應(yīng)性質(zhì),結(jié)合空間向量基本定理、模以及數(shù)量積等加以分析與求解.

其實,空間向量基本定理是建立空間向量坐標(biāo)運(yùn)算的理論依據(jù),通過空間向量的坐標(biāo)運(yùn)算,可以處理很多相關(guān)的空間向量問題,真正把空間向量的工具性展示得惟妙惟肖.